3.5E: Exercises
- Page ID
- 128868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
In exercises 1 - 30, state whether each of the following series converges absolutely, conditionally, or not at all.
1) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{n}{n+3}\)
2) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)
- Answer
- This series diverges by the Divergence Test. Terms do not tend to zero.
3) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)
4) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)
- Answer
- Converges conditionally by alternating series test, since \(\sqrt{n+3}/n\) is decreasing and its limit is 0. Does not converge absolutely by comparison with \(p\)-series, \(p=1/2\).
5) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{1}{n!}\)
6) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{3^n}{n!}\)
- Answer
- Converges absolutely by limit comparison to \(3^n/4^n,\) for example.
7) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n\)
8) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n\)
- Answer
- Diverges by Divergence Test since \(\displaystyle \lim_{n \to \infty }|a_n|=e\) and not \(0\).
9) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\sin^2n\)
10) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\cos^2n\)
- Answer
- Diverges by the Divergence Test, since its terms do not tend to zero. The limit of the sequence of its terms does not exist.
11) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\sin^2(1/n)\)
12) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\cos^2(1/n)\)
- Answer
- \(\displaystyle \lim_{n \to \infty }\cos^2(1/n)=1.\) Diverges by Divergence Test.
13) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\ln(1/n)\)
14) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})\)
- Answer
- Converges by alternating series test.
15) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)
16) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\frac{n^e}{1+n^ \pi }\)
- Answer
- Converges conditionally by alternating series test. Does not converge absolutely by limit comparison with \(p\)-series, \(p= \pi −e\)
Solution:
17) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}2^{1/n}\)
18) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}n^{1/n}\)
- Answer
- Diverges; terms do not tend to zero.
19) \(\displaystyle \sum^ \infty _{n=1}(−1)^n(1−n^{1/n})\) (Hint: \(n^{1/n} \approx 1+\ln(n)/n\) for large \(n\).)
20) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)\) (Hint: \(\cos(1/n) \approx 1−1/n^2\) for large \(n\).)
- Answer
- Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.
21) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})\) (Hint: Rationalize the numerator.)
22) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)\) (Hint: Cross-multiply then rationalize numerator.)
- Answer
- Converges absolutely by limit comparison with \(p\)-series, \(p=3/2\), after applying the hint.
23) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)\)
24) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)\) (Hint: Use Mean Value Theorem.)
- Answer
- Converges by alternating series test since \( n(\tan^{−1}(n+1)−\tan^{−1}n)\) is decreasing to zero for large \(n\).Does not converge absolutely by limit comparison with harmonic series after applying hint.
25) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}((n+1)^2−n^2)\)
26) \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)\)
- Answer
- Converges absolutely, since \( a_n=\dfrac{1}{n}−\dfrac{1}{n+1}\) are terms of a telescoping series.
27) \(\displaystyle \sum^ \infty _{n=1}\frac{\cos(n \pi )}{n}\)
28) \(\displaystyle \sum^ \infty _{n=1}\frac{\cos(n \pi )}{n^{1/n}}\)
- Answer
- Terms do not tend to zero. Series diverges by Divergence Test.
29) \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n}\sin(\frac{n \pi }{2})\)
30) \(\displaystyle \sum^ \infty _{n=1}\sin(n \pi /2)\sin(1/n)\)
- Answer
- Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.
In exercises 31 - 36, use the estimate \(|R_N| \leq b_{N+1}\) to find a value of \(N\) that guarantees that the sum of the first \(N\) terms of the alternating series \(\displaystyle \sum^ \infty _{n=1}(−1)^{n+1}b_n\) differs from the infinite sum by at most the given error. Calculate the partial sum \(S_N\) for this \(N\).
31) [Technology Required] \(b_n=1/n,\) error \( <10^{−5}\)
32) [Technology Required] \(b_n=1/\ln(n), n \geq 2,\) error \(<10^{−1}\)
- Answer
- \( \ln(N+1)>10, N+1>e^{10}, N \geq 22026; S_{22026}=0.0257 \ldots \)
33) [Technology Required] \(b_n=1/\sqrt{n},\) error \(<10^{−3}\)
34) [Technology Required] \(b_n=1/2^n\), error \(<10^{−6}\)
- Answer
- \(2^{N+1}>10^6\) or \(N+1>6\ln(10)/\ln(2)=19.93.\) or \(N \geq 19; S_{19}=0.333333969 \ldots \)
35) [Technology Required] \(b_n=ln(1+\dfrac{1}{n}),\) error \( <10^{−3}\)
36) [Technology Required] \(b_n=1/n^2,\) error \(<10^{−6}\)
- Answer
- \((N+1)^2>10^6\) or \(N>999; S_{1000} \approx 0.822466.\)
For exercises 37 - 45, indicate whether each of the following statements is true or false. If the statement is false, provide an example in which it is false.
37) If \( b_n \geq 0\) is decreasing and \(\displaystyle \lim_{n \to \infty }b_n=0\), then \(\displaystyle \sum_{n=1}^ \infty (b_{2n−1}−b_{2n})\) converges absolutely.
38) If \( b_n \geq 0\) is decreasing, then \(\displaystyle \sum_{n=1}^ \infty (b_{2n−1}−b_{2n})\) converges absolutely.
- Answer
- True. \(b_n\) need not tend to zero since if \(\displaystyle c_n=b_n−\lim b_n\), then \(c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)
39) If \( b_n \geq 0\) and \(\displaystyle \lim_{n \to \infty }b_n=0\) then \(\displaystyle \sum_{n=1}^ \infty (\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) converges.
40) If \(b_n \geq 0\) is decreasing and \(\displaystyle \sum_{n=1}^ \infty (b_{3n−2}+b_{3n−1}−b_{3n})\) converges then \(\displaystyle \sum_{n=1}^ \infty b_{3n−2}\) converges.
- Answer
- True. \(b_{3n−1}−b_{3n} \geq 0,\) so convergence of \(\displaystyle \sum b_{3n−2}\) follows from the Comparison Test.
41) If \(b_n \geq 0\) is decreasing and \(\displaystyle \sum_{n=1}^ \infty (−1)^{n−1}b_n\) converges conditionally but not absolutely, then \(b_n\) does not tend to zero.
42) Let \(a^+_n=a_n\) if \(a_n \geq 0\) and \( a^−_n=−a_n\) if \(a_n<0\). (Also, \( a^+_n=0\) if \(a_n<0\) and \(a^−_n=0\) if \(a_n \geq 0\).) If \(\displaystyle \sum_{n=1}^ \infty a_n\) converges conditionally but not absolutely, then neither \(\displaystyle \sum_{n=1}^ \infty a^+_n\) nor \(\displaystyle \sum_{n=1}^ \infty a^−_n\) converge.
- Answer
- True. If one converges, then so must the other, implying absolute convergence.
43) Suppose that \(a_n\) is a sequence of positive real numbers and that \(\displaystyle \sum_{n=1}^ \infty a_n\) converges.
44) Suppose that \(b_n\) is an arbitrary sequence of ones and minus ones. Does \(\displaystyle \sum_{n=1}^ \infty a_nb_n\) necessarily converge?
45) Suppose that \(a_n\) is a sequence such that \(\displaystyle \sum_{n=1}^ \infty a_nb_n\) converges for every possible sequence \(b_n\) of zeros and ones. Does \(\displaystyle \sum_{n=1}^ \infty a_n\) converge absolutely?
- Answer
- Yes. Take \(b_n=1\) if \(a_n \geq 0\) and \( b_n=0\) if \(a_n<0\). Then \(\displaystyle \sum_{n=1}^ \infty a_nb_n=\sum_{n:a_n \geq 0}a_n\) converges. Similarly, one can show \(\displaystyle \sum_{n:a_n<0}a_n\) converges. Since both series converge, the series must converge absolutely.
In exercises 46 - 49, the series do not satisfy the hypotheses of the alternating series test as stated. In each case, state which hypothesis is not satisfied. State whether the series converges absolutely.
46) \(\displaystyle \sum_{n=1}^ \infty (−1)^{n+1}\frac{\sin^2n}{n}\)
47) \(\displaystyle \sum_{n=1}^ \infty (−1)^{n+1}\frac{\cos^2n}{n}\)
- Answer
- Not decreasing. Does not converge absolutely.
48) \(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+ \cdots \)
49) \(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+ \cdots \)
- Answer
- Not alternating. Can be expressed as \(\displaystyle \sum_{n=1}^ \infty \left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),\) which diverges by comparison with \(\displaystyle \sum_{n=1}^ \infty \frac{1}{3n−2}.\)
50) Show that the alternating series \(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+ \cdots \) does not converge. What hypothesis of the alternating series test is not met?
51) Suppose that \(\displaystyle \sum a_n\) converges absolutely. Show that the series consisting of the positive terms \(a_n\) also converges.
- Answer
- Let \(a^+_n=a_n\) if \(a_n \geq 0\) and \(a^+_n=0\) if \( a_n<0\). Then \(a^+_n \leq |a_n|\) for all \(n\) so the sequence of partial sums of \( a^+_n\) is increasing and bounded above by the sequence of partial sums of \( |a_n|\), which converges; hence, \(\displaystyle \sum_{n=1}^ \infty a^+_n\) converges.
52) Show that the alternating series \(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+ \cdots \) does not converge. What hypothesis of the alternating series test is not met?
53) The formula \(\displaystyle \cos \theta =1−\frac{ \theta ^2}{2!}+\frac{ \theta ^4}{4!}−\frac{ \theta ^6}{6!}+ \cdots \) will be derived in the next chapter. Use the remainder \(|R_N| \leq b_{N+1}\) to find a bound for the error in estimating \(\cos \theta \) by the fifth partial sum \(1− \theta ^2/2!+ \theta ^4/4!− \theta ^6/6!+ \theta ^8/8!\) for \( \theta =1, \theta = \pi /6,\) and \( \theta = \pi .\)
- Answer
- For \(N=5\) one has \(∣R_N∣b_6= \theta ^{10}/10!\). When \( \theta =1, R_5 \leq 1/10! \approx 2.75 \times 10^{−7}\). When \( \theta = \pi /6,\) \(R_5 \leq ( \pi /6)^{10}/10! \approx 4.26 \times 10^{−10}\). When \( \theta = \pi , R_5 \leq \pi ^{10}/10!=0.0258.\)
54) The formula \(\sin \theta = \theta −\dfrac{ \theta ^3}{3!}+\dfrac{ \theta ^5}{5!}−\dfrac{ \theta ^7}{7!}+ \cdots \) will be derived in the next chapter. Use the remainder \(|R_N| \leq b_{N+1}\) to find a bound for the error in estimating \(\sin \theta \) by the fifth partial sum \( \theta − \theta ^3/3!+ \theta ^5/5!− \theta ^7/7!+ \theta ^9/9!\) for \( \theta =1, \theta = \pi /6,\) and \( \theta = \pi .\)
55) How many terms in \(\cos \theta =1−\dfrac{ \theta ^2}{2!}+\dfrac{ \theta ^4}{4!}−\dfrac{ \theta ^6}{6!}+ \cdots \) are needed to approximate \(\cos 1\) accurate to an error of at most \( 0.00001\)?
- Answer
- Let \( b_n=1/(2n−2)!.\) Then \(R_N \leq 1/(2N)!<0.00001\) when \((2N)!>10^5\) or \(N=5\) and \(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325 \ldots \), whereas \(\cos 1=0.5403023 \ldots \)
56) How many terms in \(\sin \theta = \theta −\dfrac{ \theta ^3}{3!}+\dfrac{ \theta ^5}{5!}−\dfrac{ \theta ^7}{7!}+ \cdots \) are needed to approximate \(\sin 1\) accurate to an error of at most \(0.00001?\)
57) Sometimes the alternating series \(\displaystyle \sum_{n=1}^ \infty (−1)^{n−1}b_n\) converges to a certain fraction of an absolutely convergent series \(\displaystyle \sum_{n=1}^ \infty b_n\) at a faster rate. Given that \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^2}=\frac{ \pi ^2}{6}\), find \(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+ \cdots \). Which of the series \(\displaystyle 6\sum_{n=1}^ \infty \frac{1}{n^2}\) and \(\displaystyle S\sum_{n=1}^ \infty \frac{(−1)^{n−1}}{n^2}\) gives a better estimation of \( \pi ^2\) using \(1000\) terms?
- Answer
- Let \(\displaystyle T=\sum\frac{1}{n^2}.\) Then \(T−S=\dfrac{1}{2}T\), so \(S=T/2\). \(\displaystyle \sqrt{6 \times \sum_{n=1}^{1000}1/n^2}=3.140638 \ldots ; \sqrt{\frac{1}{2} \times \sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591 \ldots ; \pi =3.141592 \ldots .\) The alternating series is more accurate for \(1000\) terms.
The alternating series in exercises 58 & 59 converge to given multiples of \( \pi \). Find the value of \(N\) predicted by the remainder estimate such that the \(N^{\text{th}}\) partial sum of the series accurately approximates the left-hand side to within the given error. Find the minimum \(N\) for which the error bound holds, and give the desired approximate value in each case. Up to \(15\) decimals places, \( \pi =3.141592653589793 \ldots .\)
58) [Technology Required] \(\displaystyle \frac{ \pi }{4}=\sum_{n=0}^ \infty \frac{(−1)^n}{2n+1},\) error \(<0.0001\)
59) [Technology Required] \(\displaystyle \frac{ \pi }{\sqrt{12}}=\sum_{k=0}^ \infty \frac{(−3)^{−k}}{2k+1},\) error \(<0.0001\)
- Answer
- \(N=6, S_N=0.9068\)
60) [Technology Required] The series \(\displaystyle \sum_{n=0}^ \infty \frac{\sin(x+ \pi n)}{x+ \pi n}\) plays an important role in signal processing. Show that \(\displaystyle \sum_{n=0}^ \infty \frac{\sin(x+ \pi n)}{x+ \pi n}\) converges whenever \(0<x< \pi \). (Hint: Use the formula for the sine of a sum of angles.)
61) [Technology Required] If \(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n} \to ln2,\) what is \(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+ \cdots ?\)
- Answer
- \(\ln(2).\) The \(n^{\text{th}}\) partial sum is the same as that for the alternating harmonic series.
62) [Technology Required] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{\cos(2 \pi nx)}{n}\) for \(0 \leq x<1\). Explain why \(\displaystyle \sum_{n=1}^{100}\frac{\cos(2 \pi nx)}{n}\) diverges when \(x=0,1\). How does the series behave for other \(x\)?
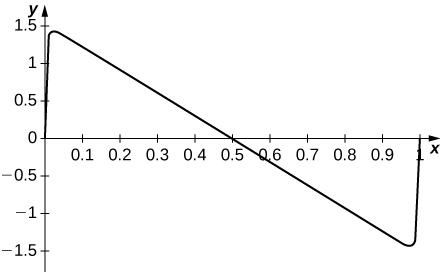
63) [Technology Required] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{\sin(2 \pi nx)}{n}\) for \(0 \leq x<1\) and comment on its behavior
- Answer
-
The series jumps rapidly near the endpoints. For \(x\) away from the endpoints, the graph looks like \( \pi (1/2−x)\).
64) [Technology Required] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{\cos(2 \pi nx)}{n^2}\) for \( 0 \leq x<1\) and describe its graph.
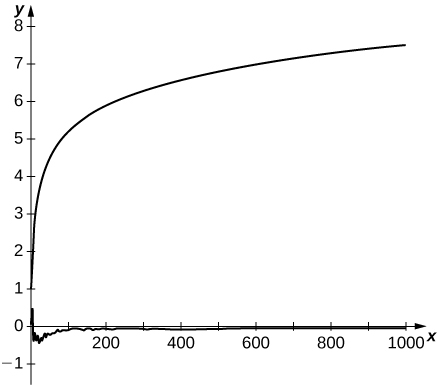
65) [Technology Required] The alternating harmonic series converges because of cancelation among its terms. Its sum is known because the cancelation can be described explicitly. A random harmonic series is one of the form \(\displaystyle \sum_{n=1}^ \infty \frac{S_n}{n}\), where \(s_n\) is a randomly generated sequence of \( \pm 1's\) in which the values \( \pm 1\) are equally likely to occur. Use a random number generator to produce \(1000\) random \( \pm 1's\) and plot the partial sums \(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) of your random harmonic sequence for \(N=1\) to \(1000\). Compare to a plot of the first \(1000\) partial sums of the harmonic series.
- Answer
-
Here is a typical result. The top curve consists of partial sums of the harmonic series. The bottom curve plots partial sums of a random harmonic series.
66) [Technology Required] Estimates of \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^2}\) can be accelerated by writing its partial sums as \(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) and recalling that \(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) converges to one as \( N \to \infty .\) Compare the estimate of \( \pi ^2/6\) using the sums \(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) with the estimate using \(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).
67) [Technology Required] The Euler transform rewrites \(\displaystyle S=\sum_{n=0}^ \infty (−1)^nb_n\) as \(\displaystyle S=\sum_{n=0}^ \infty (−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). For the alternating harmonic series, it takes the form \(\displaystyle \ln(2)=\sum_{n=1}^ \infty \frac{(−1)^{n−1}}{n}=\sum_{n=1}^ \infty \frac{1}{n2^n}\). Compute partial sums of \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n2^n}\) until they approximate \(\ln(2)\) accurate to within \(0.0001\). How many terms are needed? Compare this answer to the number of terms of the alternating harmonic series are needed to estimate \(\ln(2)\).
- Answer
- By the alternating series test, \(|S_n−S| \leq b_{n+1},\) so one needs \(10^4\) terms of the alternating harmonic series to estimate \(\ln(2)\) to within \(0.0001\). The first \(10\) partial sums of the series \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n2^n}\) are (up to four decimals) \( 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) and the tenth partial sum is within \(0.0001\) of \(\ln(2)=0.6931 \ldots .\)
68) [Technology Required] In the text it was stated that a conditionally convergent series can be rearranged to converge to any number. Here is a slightly simpler, but similar, fact. If \(a_n \geq 0\) is such that \(a_n \to 0\) as \(n \to \infty \) but \(\displaystyle \sum_{n=1}^ \infty a_n\) diverges, then, given any number \(A\) there is a sequence \(s_n\) of \( \pm 1's\) such that \(\displaystyle \sum_{n=1}^ \infty a_ns_n \to A.\) Show this for \(A>0\) as follows.
a. Recursively define \(s_n\) by \( s_n=1\) if \(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) and \( s_n=−1\) otherwise.
b. Explain why eventually \(S_n \geq A,\) and for any \(m\) larger than this \(n\), \(A−a_m \leq S_m \leq A+a_m\).
c. Explain why this implies that \( S_n \to A\) as \( n \to \infty .\)


