11.2: Partial Derivatives

Derivatives of a Function of Two Variables

When studying derivatives of functions of one variable, we found that one interpretation of the derivative is an instantaneous rate of change of \(y\) as a function of \(x.\) Leibniz notation for the derivative is \(dy/dx,\) which implies that \(y\) is the dependent variable and \(x\) is the independent variable. For a function \(z=f(x,y)\) of two variables, \(x\) and \(y\) are the independent variables and \(z\) is the dependent variable. This raises two questions right away: How do we adapt Leibniz notation for functions of two variables? Also, what is an interpretation of the derivative? The answer lies in partial derivatives.

Definition: Partial Derivatives

Let \(f(x,y)\) be a function of two variables. Then the partial derivative of \(f\) with respect to \(x\), written as \(∂f/∂x\) or \(f_x,\) is defined as

\[\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1}\]

The partial derivative of \(f\) with respect to \(y\), written as \(∂f/∂y\), or \(f_y,\) is defined as

\[\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2}\]

This definition shows two differences already. First, the notation changes, in the sense that we still use a version of Leibniz notation, but the \(d\) in the original notation is replaced with the symbol \(∂\). (This rounded \(“d”\) is usually called “partial,” so \(∂f/∂x\) is spoken as the “partial of \(f\) with respect to \(x\).”) This is the first hint that we are dealing with partial derivatives. Second, we now have two different derivatives we can take, since there are two different independent variables. Depending on which variable we choose, we can come up with different partial derivatives altogether, and often do.

Example \(\PageIndex{1}\): Calculating Partial Derivatives from the Definition

Use the definition of the partial derivative as a limit to calculate \(∂f/∂x\) and \(∂f/∂y\) for the function

\[f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber\]

Solution

First, calculate \(f(x+h,y).\)

\[\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \]

Next, substitute this into Equation \ref{pd1} and simplify:

\[\begin{align*} \dfrac{∂f}{∂x} &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\
&=\lim_{h→0}\dfrac{(x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12)−(x^2−3xy+2y^2−4x+5y−12)}{h} \\ &=\lim_{h→0}\dfrac{x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12−x^2+3xy−2y^2+4x−5y+12}{h} \\
&=\lim_{h→0}\dfrac{2xh+h^2−3hy−4h}{h}\\
&=\lim_{h→0}\dfrac{h(2x+h−3y−4)}{h} \\
&=\lim_{h→0}(2x+h−3y−4) \\
&=2x−3y−4. \end{align*}\]

To calculate \(\dfrac{∂f}{∂y}\), first calculate \(f(x,y+h):\)

\[\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}\]

Next, substitute this into Equation \ref{pd2} and simplify:

\[ \begin{align*} \dfrac{∂f}{∂y} &=\lim_{h→0}\dfrac{f(x,y+h)−f(x,y)}{h} \\
&=\lim_{h→0}\dfrac{(x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12)−(x^2−3xy+2y^2−4x+5y−12)}{h} \\ &=\lim_{h→0}\dfrac{x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12−x^2+3xy−2y^2+4x−5y+12}{h} \\
&=\lim_{h→0}\dfrac{−3xh+4yh+2h^2+5h}{h} \\
&=\lim_{h→0}\dfrac{h(−3x+4y+2h+5)}{h} \\
&=\lim_{h→0}(−3x+4y+2h+5) \\
&=−3x+4y+5 \end{align*}\]

Exercise \(\PageIndex{1}\)

Use the definition of the partial derivative as a limit to calculate \(∂f/∂x\) and \(∂f/∂y\) for the function

\[f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber\]

Hint

Use Equations \ref{pd1} and \ref{pd2} from the definition of partial derivatives.

Answer

\(\dfrac{∂f}{∂x}=8x+2y+3\)

\(\dfrac{∂f}{∂y}=2x−2y−2\)

Note: All differentiation rules you learned in Math 400 (product rule, quotient rule, chain rule, etc.) still apply.

Example \(\PageIndex{2}\): Calculating Partial Derivatives

Calculate \(∂f/∂x\) and \(∂f/∂y\) for the following functions by holding the opposite variable constant then differentiating:

1. \(f(x,y)=x^2−3xy+2y^2−4x+5y−12\)
2. \(g(x,y)=\sin(x^2y−2x+4)\)

Solution:

a. To calculate \(∂f/∂x\), treat the variable \(y\) as a constant. Then differentiate \(f(x,y)\) with respect to \(x\) using the sum, difference, and power rules:

\[\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}\]

The derivatives of the third, fifth, and sixth terms are all zero because they do not contain the variable \(x\), so they are treated as constant terms. The derivative of the second term is equal to the coefficient of \(x\), which is \(−3y\). Calculating \(∂f/∂y\):

\[\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \]

These are the same answers obtained in Example \(\PageIndex{1}\).

b. To calculate \(∂g/∂x,\) treat the variable y as a constant. Then differentiate \(g(x,y)\) with respect to \(x\) using the chain rule and power rule:

\[\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}\]

To calculate \(∂g/∂y,\) treat the variable \(x\) as a constant. Then differentiate \(g(x,y)\) with respect to \(y\) using the chain rule and power rule:

\[ \begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \]

Exercise \(\PageIndex{2}\)

Calculate \(∂f/∂x\) and \(∂f/∂y\) for the function

\[f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber\]

by holding the opposite variable constant, then differentiating.

Hint

Use Equations \ref{pd1} and \ref{pd1} from the definition of partial derivatives.

Answer

\(\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)\)

\(\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)\)

Note: The remainder of this section is not necessary for Math 420. I am leaving it for those who may wish to have a better understanding of the concepts discussed here.

How can we interpret these partial derivatives? Recall that the graph of a function of two variables is a surface in \(R^3\). If we remove the limit from the definition of the partial derivative with respect to \(x\), the difference quotient remains:

\[\dfrac{f(x+h,y)−f(x,y)}{h}.\]

This resembles the difference quotient for the derivative of a function of one variable, except for the presence of the \(y\) variable. Figure \(\PageIndex{1}\) illustrates a surface described by an arbitrary function \(z=f(x,y).\)

Figure \(\PageIndex{1}\): Secant line passing through the points \((x,y,f(x,y))\) and \((x+h,y,f(x+h,y)).\)

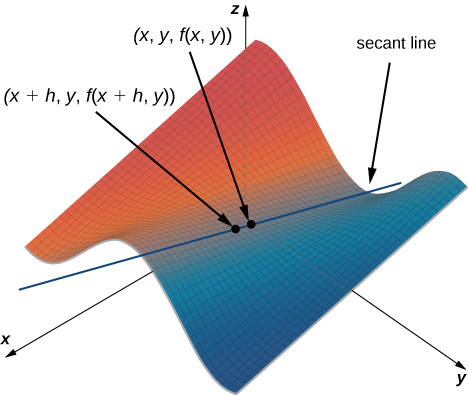
In Figure \(\PageIndex{1}\), the value of \(h\) is positive. If we graph \(f(x,y)\) and \(f(x+h,y)\) for an arbitrary point \((x,y),\) then the slope of the secant line passing through these two points is given by

\[\dfrac{f(x+h,y)−f(x,y)}{h}.\]

This line is parallel to the \(x\)-axis. Therefore, the slope of the secant line represents an average rate of change of the function \(f\) as we travel parallel to the \(x\)-axis. As \(h\) approaches zero, the slope of the secant line approaches the slope of the tangent line.

If we choose to change \(y\) instead of \(x\) by the same incremental value \(h\), then the secant line is parallel to the \(y\)-axis and so is the tangent line. Therefore, \(∂f/∂x\) represents the slope of the tangent line passing through the point \((x,y,f(x,y))\) parallel to the \(x\)-axis and \(∂f/∂y\) represents the slope of the tangent line passing through the point \((x,y,f(x,y))\) parallel to the \(y\)-axis. If we wish to find the slope of a tangent line passing through the same point in any other direction, then we need what are called directional derivatives, which is another topic from Math 402 (multivariable calculus).