1.2: Converting between Fractions - Decimals and Percents
- Page ID
- 19626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Outcomes
- Given a decimal, convert it to a percent
- Given a percent, convert it to a decimal
- Convert a fraction to a decimal and percent
In this section, we will convert from decimals to percents and back. We will also start with a fraction and convert it to a decimal and a percent. In statistics we are often given a number as a percent and have to do calculations on it. To do so, we must first convert it to a percent. Also, the computer or calculator shows numbers as decimals, but for presentations, percents are friendlier. It is also much easier to compare decimals than fractions, thus converting to a decimal is helpful.
For example, we often want to see if a probability is greater than 5%. A computer will display the probability as a decimal such as 0.04836. To make the comparison we will first change it to a percent and then compare it to 5%.
Transforming a Decimal to a Percent
We have all heard of percents before. "You only have a 20% chance of winning the game", "Just 38% of all Americans approve of Congress", and "I am 95% confident that my answer is correct" are just a few of the countless examples of percents as they come up in statistics.
Defintion: Percent
Percent means Parts Per Hundred
Thus if we are given a decimal and want to convert it to a percent, we multiply the decimal by 100. In practice, this means we move the decimal point two places to the right.
Example \(\PageIndex{1}\)
Convert the number 0.1738 to a percent.
Solution
We move the decimal over two to the right as shown below.

We get: 17.38% for the answer.
Example \(\PageIndex{2}\)
Convert 0.7 to a percent.
Solution
We want to move the decimal two places to the right, but there is only one digit to the right of the decimal place. The good news is that we can always add a 0 to the right of the last digit. We write:
\[0.7 = 0.70 \nonumber\]
Now move the decimal place two digits to the right to get 70%.
Example \(\PageIndex{3}\)
In regression analysis, an important number that is calculated is called R-Squared. It helps us determine how helpful one variable is in predicting another variable. The computer and calculator always display it as a decimal, but it is more meaningful as a percent. Suppose that the R-Squared value that relates the amount of studying students do to prepare for a final exam and the score on the exam is: \(r^2=0.8971\). Convert this to a percent rounded to the nearest whole number percent.
Solution
We move the decimal 0.8971 two places to the right to get 89.71%
Now round to the nearest whole number percent. Note that the digit to the left of the whole number is 7 > 5. Thus we add 1 to the whole number, 89. This gives us 90%.
Exercise
A standard goal in statistics is to come up with a range of values that a population proportion is likely to lie. This range is called a confidence interval. Suppose that we want to interpret a confidence interval for the percent of patients who experience side effects from an experimental cancer treatment. The computer calculates it as the decimal range: [0.023,0.029]. What is the likely range for the percent of patients who experience side effects from the experimental cancer treatment?
Transforming a Percent to a Decimal
To convert a decimal to a percent, we multiply the decimal by 100 which is equivalent to moving the decimal two places to the right. Not surprisingly, to convert a percent to a decimal, we do exactly the opposite. We divide the number by 100 which is equivalent to moving the decimal two places to the left.
Example \(\PageIndex{4}\)
Convert the percent 89.4% to a decimal.
Solution
We move the decimal over two to the left as shown below.
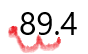
We get: 0.894 for the answer.
Example \(\PageIndex{5}\)
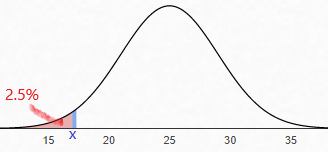
Suppose that you want to find the value of \(x\) such that 2.5% of the entire area under the Normal curve lies to the left of \(x\). The first step will be to convert the 2.5% to a decimal. What decimal is equivalent to 2.5%?
Solution
We want to move the decimal 2.5 two places to the left, but since there is only one digit to the left of the decimal, we add a zero first: 02.5. Now move the decimal two places to the left to get 0.025.
Converting a Fraction to a Decimal and a Percent
Often in probability it is natural to represent probabilities as fractions, but it is easier to make comparisons as decimals. Thus, we need to be able to convert fractions to decimals. To do so we just divide.
Example \(\PageIndex{6}\)
Convert the fraction \(\frac{4}{7}\) to a decimal, rounding to the nearest hundredth.
Solution
We use long division:
\[\hspace{0.55cm}.571\\7\overline{)4.000}\\\hspace{0.35cm}\underline{35}\\\hspace{0.5cm}50\\\hspace{0.5cm}\underline{49}\\\hspace{0.45cm}\hspace{0.25cm}10\]
Next round to the nearest hundredth to get 0.57.
Although everyone's favorite thing to do is to perform long division by hand, in most statistics classes you will have a calculator or computer to use. Thus you just have to remember to perform the division with the calculator or computer and then round.
Example \(\PageIndex{7}\)
In statistics we need to find basic probabilities and create a table for them. Suppose that you roll two six-sided dice, what percent of the time will the sum equal to a 4? Round to the nearest whole number percent.
Solution
First, notice that there are 36 total possibilities for rolling the dice, since there are 6 faces on the first die and for each value of the first die roll, there are 6 possibilities for the second die roll. Multiplying: 6 x 6 = 36. This will be the denominator. To find the numerator, we list all the possible outcome where the sum is 4:
(1,3), (2,2), and (3,1)
There are three possible outcomes with the sum equaling a 4. Thus:
\[P(\text{sum} = 4) = 3/36 \nonumber\]
Now we divide:
\[\frac{3}{36}\:=\:0.08333... \nonumber\]
Next to convert this decimal to a percent, we move the decimal two places to the right to get: 8.333...%
We are asked to round to the nearest whole number percent. The digit to the right or the whole number (8) is a 3. Since 3 < 5, we can just erase everything to the left of the 8 and leave the 8 unchanged to get 8%. Thus there is an 8% chance of getting a sum of 4 if you roll two six sided dice.


