8.4: Trigonometric Substitution

In the previous section, you learned how to decompose rational expressions into simpler forms that were easier to integrate. This section investigates a method for transforming integrands involving radical expressions of the form \(\sqrt{a^2-x^2}\), \(\sqrt{a^2+x^2}\) and \(\sqrt{x^2-a^2}\) using a specialized change of variable.

While we know that \(\int \frac{1}{\sqrt{1-x^2}}\ dx = \arcsin(x) + C\), and while we can compute \(\int \frac{x}{\sqrt{1-x^2}}\ dx\) and \(\int x\sqrt{1-x^2} \ dx\) without much difficulty using the substitution \(u = 1-x^2\), the simpler-looking integral \(\int {\sqrt{1-x^2}}\ dx\) poses a greater challenge. It does, however, have a geometric interpretation that allows us to find an antiderivative.

Consider \(\int_0^b {\sqrt{1-x^2}}\ dx\) for any \(b\) with \(0<b<1\). This definite integral represents the area of the region under the curve \(y = \sqrt{1-x^2}\) between the \(y\)-axis (where \(x=0\)) and the vertical line \(x=b\). We can split this region into two pieces, a sector of a circle and a triangle:

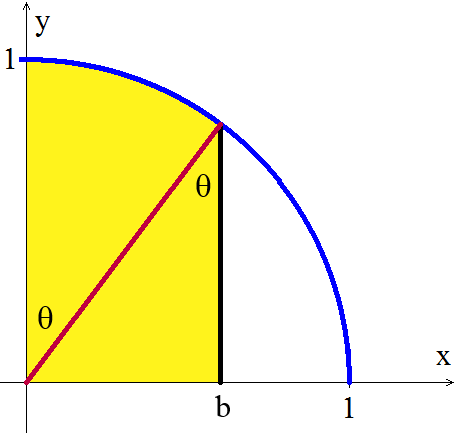
The triangle has base \(b\) and height \(\sqrt{1-b^2}\), so its area is \(\frac12 b\cdot\sqrt{1-b^2}\). The area of a sector of a circle with radius \(r\) and central angle \(\theta\) is \(\frac{\theta}{2\pi}\cdot\pi r^2 = \frac12 r^2 \theta\). But \(r=1\) and \(\theta\) is also the angle of the upper vertex of the triangle, so:\[\sin(\theta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{b}{1} = b \ \Rightarrow \ \theta = \arcsin(b)\nonumber\]which tells us:\[\int_0^b {\sqrt{1-x^2}}\ dx = \frac12 b\cdot\sqrt{1-b^2} + \frac12\arcsin(b)\nonumber\]

Note

If \(b = 1\), the integral should give the area of a quarter-circle of radius \(1\), and we can then verify that:
\begin{align*}\int_0^1 {\sqrt{1-x^2}}\ dx &= \frac12 \cdot 1\cdot 0 + \frac12\arcsin(1) \\
&= 0 + \frac12\cdot\frac{\pi}{2} = \frac{\pi}{4}\end{align*}

We can then easily deduce that:\[\int {\sqrt{1-x^2}}\ dx = \frac12 x\cdot\sqrt{1-x^2} + \frac12\arcsin(x)+C\nonumber\]The appearance of \(\arcsin(x)\) in the antiderivative of \(\sqrt{1-x^2}\) suggests a somewhat unusual substitution. Because \(\arcsin(x)\) represents an angle, we can call it \(\theta\) and write:\[\arcsin(x) = \theta \ \Rightarrow \ x = \sin(\theta) \ \Rightarrow \ dx = \cos(\theta) \, d\theta\nonumber\]If we make the substitution \(x = \sin(\theta)\), the integral becomes:
\begin{align*}\int \sqrt{1-x^2}\, dx &= \int \sqrt{1-\sin^2(\theta)} \cdot \cos(\theta) \, d\theta = \int \sqrt{\cos^2(\theta)}\cdot \cos(\theta)\, d\theta \\
&= \int \cos(\theta)\cdot \cos(\theta) \, d\theta = \int \cos^2(\theta)\, d\theta
\end{align*}

Note

Ordinarily we would write:\[\sqrt{\cos^2(\theta)} = \left|\cos(\theta)\right|\nonumber\]but \(\theta = \arcsin(x)\) and the range of arcsine is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\), so \(\cos(\theta) \geq 0\).

This is an integral we already know how to work out:
\begin{align*}\int \cos^2(\theta)\, d\theta &= \int \left[\frac12 + \frac12 \cos(2\theta)\right]\, d\theta = \frac12\theta + \frac14 \sin(2\theta) + C\\
&= \frac12\theta + \frac14 \cdot 2\sin(\theta)\cos(\theta) + C = \frac12\theta + \frac12 \sin(\theta)\cos(\theta) + C\end{align*}
Now we must convert the variable \(\theta\) back to \(x\). We started out with \(\theta = \arcsin(x) \Rightarrow x = \sin(\theta)\) so we just need to rewrite \(\cos(\theta)\) in terms of \(x\). The Pythagorean identity tells us that:\[\cos^2(\theta)+\sin^2(\theta) = 1 \ \Rightarrow \cos^2(\theta) = 1-\sin^2(\theta) = 1-x^2\nonumber\]so \(\cos(\theta) = \sqrt{1-x^2}\).

Note

Ordinarily we would write:\[\cos(\theta) = \pm\sqrt{1-x^2}\nonumber\]but from the discussion in the preceding margin note we know that \(\cos(\theta) \geq 0\).

Therefore:\[\frac12\theta + \frac12 \sin(\theta)\cos(\theta) + C = \frac12\arcsin(x) + \frac12\cdot x \cdot \sqrt{1-x^2} + C\nonumber\]which agrees with our original geometric result.

Another Change of Variable

The preceding discussion suggests a new type of substitution: instead of setting \(u = \) function of \(x\), replace \(x\) with a (trigonometric) function of \(\theta\). Each trigonometric substitution will involve four major steps:

1. Choose a substitution to make \(x\) = a trigonometric function of \(\theta\).
2. Rewrite the original integral in terms of \(\theta\) and \(d\theta\).
3. Find an antiderivative of the new integrand.
4. Rewrite this antiderivative in terms of the original variable \(x\).

The discussion that follows examines how these steps play out in three situations. The first step requires you to make a decision. The other steps follow from that decision. For most students, the key to success with the Trigonometric Substitution technique is to think triangles.

Step 1: Choosing the substitution

The Pythagorean identity \(\cos^2(\theta) + \sin^2(\theta) = 1\) played an important role in our first application of the trigonometric substitution technique. The familiar Pythagorean Theorem can help guide you to a correct choice of substitution so that a trigonometric identity will always come to the rescue when converting from \(\theta\) back to \(x\) in Step 4. Thinking of a right triangle, we can
state the Pythagorean Theorem as:
\begin{align*}\left(\mbox{side}\right)^2 &+ \left(\mbox{other side}\right)^2 = \left(\mbox{hypotenuse}\right)^2 \\
&\Rightarrow \ \left(\mbox{other side}\right)^2 = \left(\mbox{hypotenuse}\right)^2 - \left(\mbox{side}\right)^2\end{align*}
A right triangle representing our initial substitution \(x = \sin(\theta)\) appears below:

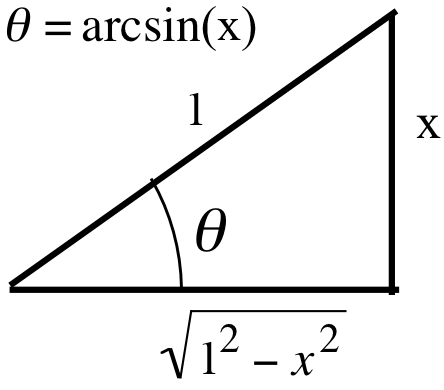
Here \(x\) is the length of the side opposite \(\theta\) and \(1\) is the length of the hypotenuse, so that the “other side” has length \(\sqrt{1-x^2}\), the radical expression that appeared in the original integral.

We now investigate the trigonometric substitutions for three representative patterns: \(3^2+x^2\), \(3^2-x^2\) and \(x^2-3^2\). (There is nothing special about the number \(3\) in these examples: we would have used \(5\) or \(\pi\) or \(\sqrt{17}\).)

• The pattern \(\boldsymbol{3^2 + x^2}\) matches the Pythagorean pattern if \(3\) and \(x\) are sides of a right triangle:
  
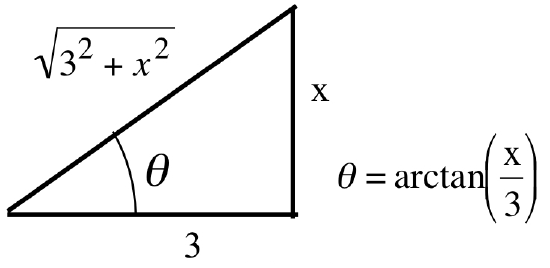
  Then:\[\tan(\theta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{x}{3} \ \Rightarrow \ x = 3\tan(\theta)\nonumber\]
• The pattern \(\boldsymbol{3^2 - x^2}\) matches the Pythagorean pattern if \(3\) is the hypotenuse and \(x\) is a side of a right triangle:
  
  Then:\[\sin(\theta) = \frac{\mbox{opposite}}{\mbox{hypotenuse}} = \frac{x}{3} \ \Rightarrow \ x = 3\sin(\theta)\nonumber\]
• The pattern \(\boldsymbol{x^2 - 3^2}\) matches the Pythagorean pattern if \(x\) is the hypotenuse and \(3\) is a side of a right triangle:
  
  Then:\[\sec(\theta) = \frac{\mbox{hypotenuse}}{\mbox{adjacent}} = \frac{x}{3} \ \Rightarrow \ x = 3\sec(\theta)\nonumber\]

Step 2: Rewrite the original integral in terms of \(\theta\) and \(d\theta\)

Once you have made the choice for the substitution, several things follow automatically: you can easily calculate \(dx\), you can solve for \(\theta\), and you can rewrite the original pattern of interest as a function of \(\theta\).

• With the pattern \(\boldsymbol{3^2 + x^2}\), differentiation yields:\[x = 3\tan(\theta) \ \Rightarrow \ dx = 3\sec^2(\theta)\, d\theta\nonumber\]while solving the substitution equation for \(\theta\) yields:\[x = 3\tan(\theta) \ \Rightarrow \ \tan(\theta) = \frac{x}{3} \ \Rightarrow \ \theta = \arctan\left(\frac{x}{3}\right)\nonumber\]and the original pattern becomes:\[3^2+x^2 = 3^2+3^2\tan^2(\theta) = 3^2\left[1+\tan^2(\theta)\right] = 3^2\sec^2(\theta)\nonumber\](Here \(-\frac{\pi}{2} < \theta < \frac{\pi}{2}\) because that is the range of the arctangent function. This means that \(\sec(\theta) > 0\) always holds, so that \(\sqrt{\sec^2(\theta)} = \sec(\theta)\).)
• With the pattern \(\boldsymbol{3^2 - x^2}\), differentiation yields:\[x = 3\sin(\theta) \ \Rightarrow \ dx = 3\cos(\theta)\, d\theta\nonumber\]while solving the substitution equation for \(\theta\) yields:\[x = 3\sin(\theta) \ \Rightarrow \ \sin(\theta) = \frac{x}{3} \ \Rightarrow \ \theta = \arcsin\left(\frac{x}{3}\right)\nonumber\]and the original pattern becomes:\[3^2-x^2 = 3^2-3^2\sin^2(\theta) = 3^2\left[1-\sin^2(\theta)\right] = 3^2\cos^2(\theta)\nonumber\](Here \(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\) because that is the range of the arcsine function. This means that \(\cos(\theta) \geq 0\) always holds, so that \(\sqrt{\cos^2(\theta)} = \cos(\theta)\).)
• With the pattern \(\boldsymbol{x^2-3^2}\), differentiation yields:\[x = 3\sec(\theta) \ \Rightarrow \ dx = 3\sec(\theta)\tan(\theta)\, d\theta\nonumber\]while solving the substitution equation for \(\theta\) yields:\[x = 3\sec(\theta) \ \Rightarrow \ \sec(\theta) = \frac{x}{3} \ \Rightarrow \ \theta = \mbox{arcsec}\left(\frac{x}{3}\right)\nonumber\]and the original pattern becomes:\[x^2-3^2 = 3^2\sec^2(\theta)-3^2 = 3^2\left[\sec^2(\theta)-1\right] = 3^2\tan^2(\theta)\nonumber\](Here \(0 \leq \theta < \frac{\pi}{2}\) or \(\frac{\pi}{2} < \theta < \pi\) because that is the range of the arcsecant function. We will want \(\tan(\theta) \geq 0\) to avoid absolute values when simplifying \(\sqrt{\tan^2(\theta)}\); to do so, we will need to assume that \(x \geq 3\) so that \(0 \leq \theta < \frac{\pi}{2}\).)

Example \(\PageIndex{1}\)

For the patterns \(16 - x^2\) and \(5 + x^2\), select an appropriate substitution for \(x\), calculate \(dx\) and \(\theta\), and use the substitution to simplify the pattern.

Solution

The pattern \(16 - x^2\) matches the Pythagorean pattern if \(4\) is a hypotenuse and \(x\) is the side of a right triangle:

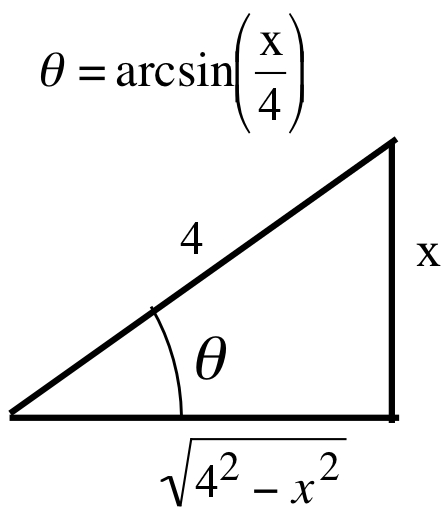
Then:\[\sin(\theta) = \frac{\mbox{opposite}}{\mbox{hypotenuse}} = \frac{x}{4} \ \Rightarrow \ x = 4\sin(\theta) \ \Rightarrow \ dx = 4\cos(\theta)\, d\theta\nonumber\]while \(\displaystyle \theta = \arcsin\left(\frac{x}{4}\right)\) and \(16 - x^2\) becomes:\[16 - \left[4\sin(\theta)\right]^2 = 16 - 16\sin^2(\theta) = 16\left[1 - \sin^2(\theta)\right] = 16\cos^2(\theta)\nonumber\]

The pattern \(5 + x^2\) matches the Pythagorean pattern if \(x\) and \(\sqrt{5}\) are the sides of a right triangle:

Then:\[\tan(\theta) = \frac{\mbox{opposite}}{\mbox{adjacent}} = \frac{x}{\sqrt{5}} \ \Rightarrow \ x = \sqrt{5}\tan(\theta) \ \Rightarrow \ dx = \sqrt{5}\sec^2(\theta)\, d\theta\nonumber\]while \(\displaystyle \theta = \arctan\left(\frac{x}{\sqrt{5}}\right)\) and \(5 + x^2\) becomes:\[5 + \left[\sqrt{5}\tan(\theta)\right]^2 = 5 + 5\tan^2(\theta) = 5\left[1 + \tan^2(\theta)\right] = 5\sec^2(\theta)\nonumber\]Drawing a right triangle for each pattern (as in the margin) will help you visualize the appropriate substitution.

Practice \(\PageIndex{1}\)

For the patterns \(25 + x^2\) and \(x^2-13\), decide on the appropriate substitution for \(x\), calculate \(dx\) and \(\theta\), and use the substitution to simplify the pattern.

Answer

For the pattern \(25 + x^2\), use \(x = 5\cdot\tan(\theta) \Rightarrow dx = 5\cdot\sec^2(\theta)\, d\theta\), while \(\displaystyle \theta = \arctan\left(\frac{x}{5}\right)\) and:\[25 + x^2 = 25 + 25\tan^2(\theta) = 25\left[1 + \tan^2(\theta)\right] = 25\sec^2(\theta)\nonumber\]For \(x^2 - 13\), use \(x = \sqrt{13}\sec(\theta) \Rightarrow dx = \sqrt{13}\sec(\theta)\cdot\tan(\theta)\, d\theta\), while \(\displaystyle \theta = \mbox{arcsec}\left(\frac{x}{\sqrt{13}}\right)\) and:\[x^2 - 13 = 13\sec^2(\theta) - 13 = 13\left[\sec^2(\theta) - 1\right] = 13\tan^2(\theta)\nonumber\]

Example \(\PageIndex{2}\)

Use \(x = 5\tan(\theta)\) to rewrite the integral \(\displaystyle \int \frac{1}{\sqrt{25+x^2}} \ dx\).

Solution

Differentiating \(x = 5\tan(\theta)\) yields \(dx = 5\sec^2(\theta)\, d\theta\) and:\[25 + x^2 = 25 + 25\tan^2(\theta) = 25\left[1 + \tan^2(\theta)\right] = 25\sec^2(\theta)\nonumber\]so that \(\sqrt{25+x^2} = \sqrt{25\sec^2(\theta)} = 5\sec(\theta)\) and the integral becomes:\[\int \frac{1}{\sqrt{25+x^2}} \ dx = \int \frac{1}{5\sec(\theta)} \cdot 5 \sec^2(\theta) \, d\theta = \int \sec(\theta)\, d\theta\nonumber\]which is an integral we already know how to evaluate.

Practice \(\PageIndex{2}\)

Use \(x = 5\sin(\theta)\) to rewrite the integral \(\displaystyle \int \frac{1}{\sqrt{25-x^2}} \ dx\).

Answer

\(x = 5\sin(\theta) \Rightarrow dx = 5\cos(\theta)\, d\theta\), while \(\displaystyle \theta = \arcsin\left(\frac{x}{5}\right)\) so:\[25 - x^2 = 25\left[1 - \sin^2(\theta)\right] = 25\cos^2(\theta)\nonumber\]and the integral becomes:
\begin{align*}\int \frac{1}{\sqrt{25-x^2}}\ dx &= \int \frac{1}{\sqrt{25\cos^2(\theta)}}\cdot 5\cos(\theta)\, d\theta = \frac55 \int \frac{\cos(\theta)}{\cos(\theta)}\ d\theta \\
&= \int 1\, d\theta = \theta + C = \arcsin\left(\frac{x}{5}\right) + C\end{align*}

Step 3: Find an antiderivative of the new integrand

After changing the variable, the new integrand typically involves products of powers of trigonometric functions and we can use any of our previous methods (another change of variable, integration by parts, a trigonometric identity or integral tables) to find an antiderivative.

Step 4: Rewrite this antiderivative in terms of the original variable

Once we have found an antiderivative, usually involving a trigonometric function of \(\theta\), we can replace \(\theta\) with the appropriate inverse trigonometric function of \(x\) and simplify. Because the antiderivatives commonly contain trigonometric functions, we frequently need to simplify a trigonometric function of an inverse trigonometric function, and at this stage it is often very helpful to refer back to the right triangle we used at the beginning of the substitution process.

Example \(\PageIndex{3}\)

Evaluate \(\displaystyle \int \frac{1}{\sqrt{25+x^2}}\ dx\).

Solution

In Example 2 we used the substitution \(x = 5\tan(\theta)\) to convert this integral to:\[\int \frac{1}{\sqrt{25+x^2}}\ dx = \int \sec(\theta)\, d\theta = \ln\left(\left|\sec(\theta)+\tan(\theta)\right|\right)+C\nonumber\]We now need to rewrite \(\sec(\theta)\) and \(\tan(\theta)\) in this antiderivative in terms of \(x\) using the fact that \(\displaystyle \theta = \arctan\left(\frac{x}{5}\right)\):\[\ln\left(\left|\sec\left(\arctan\left(\frac{x}{5}\right)\right)+\tan\left(\arctan\left(\frac{x}{5}\right)\right)\right|\right)+C\nonumber\]Referring to the right triangle for this substitution:

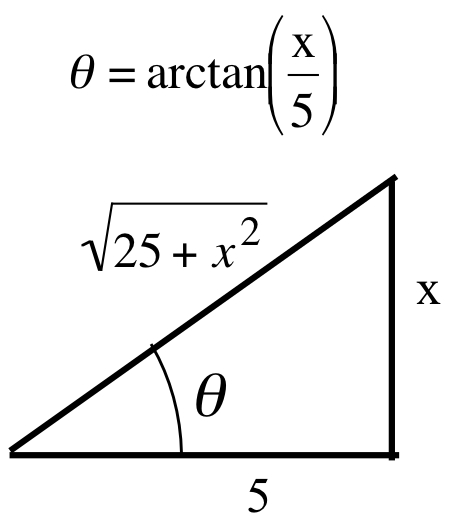
we can write\[\sec\left(\arctan\left(\frac{x}{5}\right)\right) = \frac{\sqrt{25 + x^2}}{5} \quad \mbox{and} \quad \tan\left(\arctan\left(\frac{x}{5}\right)\right) = \frac{x}{5}\nonumber\]so, putting all of these pieces together:\[\int \frac{1}{\sqrt{25+x^2}}\ dx = \ln\left(\frac{\sqrt{25 + x^2}}{5} + \frac{x}{5}\right) + C\nonumber\]As always, we can check that this is indeed an antiderivative of the original integrand by differentiating.

Where did the absolute value signs go? Because:\[-\frac{x}{5} \leq \left|\frac{x}{5}\right| = \frac{\sqrt{x^2}}{5} < \frac{\sqrt{x^2+25}}{5}\nonumber\]we know that:\[\frac{\sqrt{x^2+25}}{5} + \frac{x}{5} > 0\nonumber\]

Practice \(\PageIndex{3}\)

Evaluate \(\displaystyle \int \frac{1}{x^2\sqrt{9-x^2}}\ dx\).

Answer

Use \(x = 3\sin(\theta) \Rightarrow dx = 3\cos(\theta)\, d\theta\) while \)\displaystyle \theta = \arcsin\left(\frac{x}{2}\right)\) and:\[9 - x^2 = 9\left[1 - \sin^2(\theta)\right] = 9\cos^2(\theta)\nonumber\]Then the integral becomes:
\begin{align*}\int \frac{1}{x^2\sqrt{9 - x^2}}\ dx &= \int \frac{1}{9\sin^2(\theta)\sqrt{9\cos^2(\theta)}}\cdot 3\cos(\theta)\, d\theta\\
&= \int \frac{3\cos(\theta)}{27\sin^2(\theta)\cos(\theta)}\ d\theta = \frac19 \int \csc^2(\theta) \, d\theta\\
& = -\frac19\cot(\theta) + C = -\frac19\cot\left(\arcsin\left(\frac{x}{2}\right)\right)+ C\\
& = -\frac19\cdot\frac{\sqrt{9-x^2}}{x} + C
\end{align*}

Variations on a Theme

While we will typically apply trigonometric substitution to integrands involving radicals of the form \(\sqrt{a^2+x^2}\), \(\sqrt{a^2-x^2}\) or \(\sqrt{x^2-a^2}\), we can adapt this technique for more general integrands by incorporating other methods, such as \(u\)-substitution and completing the square.

Example \(\PageIndex{4}\)

Evaluate \(\displaystyle \int \frac{1}{\sqrt{x^2 + 2x + 26}} \ dx\).

Solution

The polynomial inside the radical in this integrand is an irreducible quadratic so — just as we did with rational functions — we can complete the square:\[x^2 + 2x + 26 = (x + 1)^2 + 25\nonumber\]and next use the substitution \(u = x + 1 \Rightarrow du = dx\):\[\int \frac{1}{\sqrt{x^2 + 2x + 26}} \ dx = \int \frac{1}{\sqrt{(x+1)^2+5^2}} \ dx = \int \frac{1}{\sqrt{u^2+5^2}} \ du\nonumber\]The integrand is now ready for a trigonometric substitution. In fact, this resembles the integral in Example 3, so: \begin{align*}\int \frac{1}{\sqrt{u^2+5^2}} \ du &= \ln\left(\frac{\sqrt{25 + u^2}}{5} + \frac{u}{5}\right) + C\\ &= \ln\left(\sqrt{25 + u^2} + u\right) + C-\ln(5)\\ &= \ln\left(\sqrt{25 + (x+1)^2} + (x+1)\right) + K \end{align*} or \(\ln\left(x+1 + \sqrt{x^2+2x+26}\right) + K\).

Here we have employed the logarithmic identity:\[\ln\left(\frac{A}{B}\right) = \ln(A)-\ln(B)\nonumber\]We could have made a similar simplification in Example 3.

Wrap-up

When using trig substitution, remember to think triangles. The first and last steps (choosing the substitution and writing the answer in terms of \(x\)) are much easier if you have drawn the appropriate triangle for the problem. Of course, you also need to practice the method.

Problems

In Problems 1–8, determine the appropriate substitution for the given integrand.

1. \(\displaystyle \sqrt{49-x^2}\)
2. \(\displaystyle \sqrt{x^2-36}\)
3. \(\displaystyle \left(81+x^2\right)^{\frac52}\)
4. \(\displaystyle \sqrt{8+x^2}\)
5. \(\displaystyle \sqrt{x^2-7}\)
6. \(\displaystyle \sqrt{99-x^2}\)
7. \(\displaystyle \frac{1}{x\sqrt{100-x^2}}\)
8. \(\displaystyle \frac{1}{x^2\sqrt{x^2-100}}\)

In Problems 9–14, make the given substitution and simplify the result, then calculate \(dx\).

9. \(x = 3\cdot\sin(\theta)\) in \(\displaystyle \frac{1}{\sqrt{9 - x^2}}\)
10. \(x = 3\cdot\tan(\theta)\) in \(\displaystyle \frac{1}{\sqrt{x^2+9}}\)
11. \(x = 3\cdot\sec(\theta)\) in \(\displaystyle \frac{1}{\sqrt{x^2-9}}\)
12. \(x = 6\cdot\sin(\theta)\) in \(\displaystyle \frac{1}{36 - x^2}\)
13. \(x = \sqrt{2}\cdot\tan(\theta)\) in \(\displaystyle \frac{1}{\sqrt{2+x^2}}\)
14. \(x = \sec(\theta)\) in \(\displaystyle \frac{1}{\sqrt{x^2-1}}\)

In Problems 15–20:

1. solve for \(\theta\) as a function of \(x\),
2. replace \(\theta\) in \(f(\theta)\) with you result from part (a), and
3. simplify.

15. \(x = 3\cdot\sin(\theta)\), \(f(\theta) = \cos(\theta)\cdot\tan(\theta)\)
16. \(x = 3\cdot\tan(\theta)\), \(f(\theta) = \sin(\theta)\cdot\tan(\theta)\)
17. \(x = 3\cdot\sec(\theta)\), \(\displaystyle f(\theta) = \sqrt{1 + \sin^2(\theta)}\)
18. \(x = 5\cdot\sin(\theta)\), \(\displaystyle f(\theta) = \frac{\cos(\theta)}{1 + \sec(\theta)}\)
19. \(x = 5\cdot\tan(\theta)\), \(\displaystyle f(\theta) = \frac{\cos^2(\theta)}{1 + \cot(\theta)}\)
20. \(x = 5\cdot\sec(\theta)\), \(f(\theta) = \cos(\theta) + 7\cdot\tan^2(\theta)\)

In Problems 21–44, evaluate the integral. (More than one method works for some of the integrals.)

21. \(\displaystyle \int \frac{1}{x\sqrt{9-x^2}} \ dx\)
22. \(\displaystyle \int \frac{x^2}{\sqrt{9-x^2}} \ dx\)
23. \(\displaystyle \int \frac{1}{\sqrt{x^2+49}} \ dx\)
24. \(\displaystyle \int \frac{1}{\sqrt{x^2+1}} \ dx\)
25. \(\displaystyle \int \sqrt{36-x^2} \ dx\)
26. \(\displaystyle \int \sqrt{1-36x^2} \ dx\)
27. \(\displaystyle \int \frac{1}{\sqrt{36+x^2}} \ dx\)
28. \(\displaystyle \int \frac{1}{x\sqrt{25-x^2}} \ dx\)
29. \(\displaystyle \int \frac{x^2}{\sqrt{49-x^2}} \ dx\)
30. \(\displaystyle \int \frac{\sqrt{25-x^2}}{x^2} \ dx\)
31. \(\displaystyle \int \frac{x}{\sqrt{25-x^2}} \ dx\)
32. \(\displaystyle \int \frac{1}{x^2+49} \ dx\)
33. \(\displaystyle \int \frac{x}{x^2+49} \ dx\)
34. \(\displaystyle \int \frac{1}{49x^2+25} \ dx\)
35. \(\displaystyle \int \frac{1}{\left(x^2-9\right)^{\frac32}} \ dx\)
36. \(\displaystyle \int \frac{1}{\left(4x^2-1\right)^{\frac32}} \ dx\)
37. \(\displaystyle \int \frac{5}{2x\sqrt{x^2-25}} \ dx\)
38. \(\displaystyle \int \frac{1}{x\sqrt{3-x^2}} \ dx\)
39. \(\displaystyle \int \frac{1}{25-x^2} \ dx\)
40. \(\displaystyle \int \frac{1}{a^2+x^2} \ dx\)
41. \(\displaystyle \int \frac{1}{\sqrt{a^2+x^2}} \ dx\)
42. \(\displaystyle \int \frac{1}{x\sqrt{a^2+x^2}} \ dx\)
43. \(\displaystyle \int \frac{1}{x^2\sqrt{a^2+x^2}} \ dx\)
44. \(\displaystyle \int \frac{1}{\left(a^2+x^2\right)^{\frac32}} \ dx\)

In Problems 45–50, complete the square and make an appropriate substitution (as necessary), then evaluate the integral.

45. \(\displaystyle \int \frac{1}{\sqrt{(x+1)^2+9}} \ dx\)
46. \(\displaystyle \int \frac{1}{\sqrt{(x+3)^2+1}} \ dx\)
47. \(\displaystyle \int \frac{1}{x^2+10x+29} \ dx\)
48. \(\displaystyle \int \frac{1}{x^2-4x+13} \ dx\)
49. \(\displaystyle \int \frac{1}{\sqrt{x^2+4x+3}} \ dx\)
50. \(\displaystyle \int \frac{1}{\sqrt{x^2-6x-16}} \ dx\)
51. The integral \(\displaystyle \int \frac{1}{(x^2+1)^2}\, dx\) arises when finding antiderivatives using partial fractions.
    1. Evaluate this integral using an appropriate trigonometric substitution.
    2. Now evaluate it using integration by parts.
    3. Which method is easier?
52. Evaluate \(\displaystyle \int \frac{1}{(x^2-8x+25)^2}\ dx\).
53. Evaluate \(\displaystyle \int \frac{8x}{(x^2+25)^2}\ dx\).