9.1E: Exercises
- Page ID
- 79532
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Solve Quadratic Equations of the form \(ax^2=k\) Using the Square Root Property
In the following exercises, solve the following quadratic equations.
\(a^2=49\)
- Answer
-
\(a=\pm7\)
\(b^2=144\)
\(r^2−24=0\)
- Answer
-
\(r=\pm2\sqrt{6}\)
\(t^2−75=0\)
\(u^2−300=0\)
- Answer
-
\(u=\pm10\sqrt{3}\)
\(v^2−80=0\)
\(4m^2=36\)
- Answer
-
\(m=\pm3\)
\(3n^2=48\)
\(x^2+20=0\)
- Answer
-
no real solution
\(y^2+64=0\)
\(\frac{2}{5}a^2+3=11\)
- Answer
-
\(a=\pm2\sqrt{5}\)
\(\frac{3}{2}b^2−7=41\)
\(7p^2+10=26\)
- Answer
-
\(p=\pm\frac{4\sqrt{7}}{7}\)
\(2q^2+5=30\)
Solve Quadratic Equations of the Form \(a(x−h)^2=k\) Using the Square Root Property
In the following exercises, solve the following quadratic equations.
\((x+2)^2=9\)
- Answer
-
x=1, x=−5
\((y−5)^2=36\)
\((u−6)^2=64\)
- Answer
-
u=14, u=−2
\((v+10)^2=121\)
\((m−6)^2=20\)
- Answer
-
\(m=6\pm2\sqrt{5}\)
\((n+5)^2=32\)
\((r−\frac{1}{2})^2=\frac{3}{4}\)
- Answer
-
\(r=\frac{1}{2}\pm\frac{\sqrt{3}}{2}\)
\((t−\frac{5}{6})^2=\frac{11}{25}\)
\((a−7)^2+5=55\)
- Answer
-
\(a=7\pm5\sqrt{2}\)
\((b−1)^2−9=39\)
\((5c+1)^2=−27\)
- Answer
-
no real solution
\((8d−6)^2=−24\)
\(m^2−4m+4=8\)
- Answer
-
\(m=2\pm2\sqrt{2}\)
\(n^2+8n+16=27\)
\(25x^2−30x+9=36\)
- Answer
-
\(x=−\frac{3}{5}\), \(x=\frac{9}{5}\)
\(9y^2+12y+4=9\)
Mixed Practice
In the following exercises, solve using the Square Root Property.
\(2r^2=32\)
- Answer
-
\(r=\pm4\)
\(4t^2=16\)
\((a−4)^2=28\)
- Answer
-
\(a=4\pm2\sqrt{7}\)
\((b+7)^2=8\)
\(9w^2−24w+16=1\)
- Answer
-
\(w=1\), \(w=\frac{5}{3}\)
\(4z^2+4z+1=49\)
\(a^2−18=0\)
- Answer
-
\(a=\pm3\sqrt{2}\)
\(b^2−108=0\)
\((p−\frac{1}{3})^2=\frac{7}{9}\)
- Answer
-
\(p=\frac{1}{3}\pm\frac{\sqrt{7}}{3}\)
\((q−\frac{3}{5})^2=\frac{3}{4}\)
\(m^2+12=0\)
- Answer
-
no real solution
\(n^2+48=0\)
\(u^2−14u+49=72\)
- Answer
-
\(u=7\pm6\sqrt{2}\)
\(v^2+18v+81=50\)
\((m−4)^2+3=15\)
- Answer
-
\(m=4\pm2\sqrt{3}\)
\((n−7)^2−8=64\)
\((x+5)^2=4\)
- Answer
-
\(x=−3\), \(x=−7\)
\((y−4)^2=64\)
\(6c^2+4=29\)
- Answer
-
\(c=\pm\frac{5\sqrt{6}}{6}\)
\(2d^2−4=77\)
\((x−6)^2+7=3\)
- Answer
-
no real solution
\((y−4)^2+10=9\)
Everyday Math
Paola has enough mulch to cover 48 square feet. She wants to use it to make three square vegetable gardens of equal sizes. Solve the equation \(3s^2=48\) to find s, the length of each garden side.
- Answer
-
4 feet
Kathy is drawing up the blueprints for a house she is designing. She wants to have four square windows of equal size in the living room, with a total area of 64 square feet. Solve the equation \(4s^2=64\) to find s, the length of the sides of the windows.
Writing Exercises
Explain why the equation \(x^2+12=8\) has no solution.
- Answer
-
Answers will vary.
Explain why the equation \(y^2+8=12\) has two solutions.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
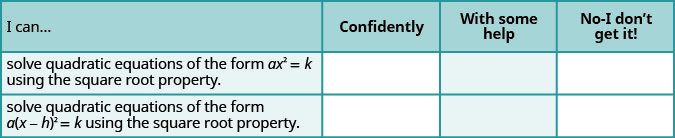
ⓑ If most of your checks were:
…confidently: Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help: This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no-I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.