5.2: Radical Functions

Evaluate a Radical Function

In this section we will extend our previous work with functions to include radicals. If a function is defined by a radical expression, we call it a radical function.

• The square root function is $f(x)=\sqrt{x}$.
• The cube root function is $f(x)=\sqrt[3]{x}$.

Definition $\PageIndex{1}$: radical function

A radical function is a function that is defined by a radical expression.

To evaluate a radical function, we find the value of $f(x)$ for a given value of $x$ just as we did in our previous work with functions.

Example $\PageIndex{1}$

For the function $f(x)=\sqrt{2 x-1}$, find

1. $f(5)$
2. $f(-2)$

Solution:

a.

$f(x)=\sqrt{2 x-1}$

To evaluate $f(5)$, substitute $5$ for $x$.

$f(5)=\sqrt{2 \cdot 5-1}$

Simplify.

$f(5)=\sqrt{9}$

Take the square root.

$f(5)=3$

b.

$f(x)=\sqrt{2 x-1}$

To evaluate $f(-2)$, substitute $-2$ for $x$.

$f(-2)=\sqrt{2(-2)-1}$

Simplify.

$f(-2)=\sqrt{-5}$

Since the square root of a negative number is not a real number, the function does not have a value at $x=-2$.

Exercise $\PageIndex{1}$

For the function $f(x)=\sqrt{3 x-2}$, find

1. $f(6)$
2. $f(0)$

Answer

1. $f(6)=4$
2. no value at $x=0$

Exercise $\PageIndex{2}$

For the function $g(x)=\sqrt{5x+5}$, find

1. $g(4)$
2. $g(-3)$

Answer

1. $g(4)=5$
2. no value at $f(-3)$

We follow the same procedure to evaluate cube roots.

Example $\PageIndex{2}$

For the function $g(x)=\sqrt[3]{x-6}$, find

1. $g(14)$
2. $g(-2)$

Solution:

a.

$g(x)=\sqrt[3]{x-6}$

To evaluate $g(14)$, substitute $14$ for $x$.

$g(14)=\sqrt[3]{14-6}$

Simplify.

$g(14)=\sqrt[3]{8}$

Take the cube root.

$g(14)=2$

b.

$g(x)=\sqrt[3]{x-6}$

To evaluate $g(-2)$, substitute $-2$ for $x$.

$g(-2)=\sqrt[3]{-2-6}$

Simplify.

$g(-2)=\sqrt[3]{-8}$

Take the cube root.

$g(-2)=-2$

Exercise $\PageIndex{3}$

For the function $g(x)=\sqrt[3]{3 x-4}$, find

1. $g(4)$
2. $g(1)$

Answer

1. $g(4)=2$
2. $g(1)=-1$

Exercise $\PageIndex{4}$

For the function $h(x)=\sqrt[3]{5 x-2}$, find

1. $h(2)$
2. $h(-5)$

Answer

1. $h(2)=2$
2. $h(-5)=-3$

The next example has fourth roots.

Example $\PageIndex{3}$

For the function $f(x)=\sqrt[4]{5 x-4}$, find

1. $f(4)$
2. $f(-12)$

Solution:

a.

$f(x)=\sqrt[4]{5 x-4}$

To evaluate $f(4)$, substitute $4$ for $x$.

$f(4)=\sqrt[4]{5 \cdot 4-4}$

Simplify.

$f(4)=\sqrt[4]{16}$

Take the fourth root.

$f(4)=2$

b.

$f(x)=\sqrt[4]{5 x-4}$

To evaluate $f(-12)$, substitute $-12$ for $x$.

$f(-12)=\sqrt[4]{5(-12)-4}$

Simplify.

$f(-12)=\sqrt[4]{-64}$

Since the fourth root of a negative number is not a real number, the function does not have a value at $x=-12$.

Exercise $\PageIndex{5}$

For the function $f(x)=\sqrt[4]{3 x+4}$, find

1. $f(4)$
2. $f(-1)$

Answer

1. $f(4)=2$
2. $f(-1)=1$

Exercise $\PageIndex{6}$

For the function $g(x)=\sqrt[4]{5 x+1}$, find

1. $g(16)$
2. $g(3)$

Answer

1. $g(16)=3$
2. $g(3)=2$

Find the Domain of a Radical Function

To find the domain and range of radical functions, we use our properties of radicals. For a radical with an even index, we said the radicand had to be greater than or equal to zero as even roots of negative numbers are not real numbers. For an odd index, the radicand can be any real number. We restate the properties here for reference.

Properties of $\sqrt[n]{a}$

When $n$ is an even number and:

• $a \geq 0$, then $\sqrt[n]{a}$ is a real number.
• $a<0$, then $\sqrt[n]{a}$ is not a real number.

When $n$ is an odd number, $\sqrt[n]{a}$ is a real number for all values of $a$.

So, to find the domain of a radical function with even index, we set the radicand to be greater than or equal to zero. For an odd index radical, the radicand can be any real number.

Domain of a Radical Function

When the index of the radical is even, the radicand must be greater than or equal to zero.

When the index of the radical is odd, the radicand can be any real number.

Example $\PageIndex{4}$

Find the domain of the function, $f(x)=\sqrt{3 x-4}$. Write the domain in interval notation.

Solution:

Since the function, $f(x)=\sqrt{3 x-4}$ has a radical with an index of $2$, which is even, we know the radicand must be greater than or equal to $0$. We set the radicand to be greater than or equal to $0$ and then solve to find the domain.

Solve.

$\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}$

The domain of $f(x)=\sqrt{3 x-4}$ is all values $x \geq \frac{4}{3}$ and we write it in interval notation as $\left[\frac{4}{3}, \infty\right)$.

Exercise $\PageIndex{7}$

Find the domain of the function, $f(x)=\sqrt{6 x-5}$. Write the domain in interval notation.

Answer

$\left[\frac{5}{6}, \infty\right)$

Exercise $\PageIndex{8}$

Find the domain of the function, $f(x)=\sqrt{4-5 x}$. Write the domain in interval notation.

Answer

$\left(-\infty, \frac{4}{5}\right]$

Example $\PageIndex{5}$

Find the domain of the function, $g(x)=\sqrt{\frac{6}{x-1}}$. Write the domain in interval notation.

Solution:

Solve the function, $g(x)=\sqrt{\frac{6}{x-1}}$ has a radical with an index of $2$, which is even, we know the radicand must be greater than or equal to $0$.

The radicand cannot be zero since the numerator is not zero.

For $\frac{6}{x-1}$ to be greater than zero, the denominator must be positive since the numerator is positive. We know a positive divided by a positive is positive.

We set $x-1>0$ and solve.

$x-1>0$

Solve.

$x>1$

Also, since the radicand is a fraction, we must realize that the denominator cannot be zero.

We solve $x-1=0$ to find the value that must be eliminated from the domain.

$x-1=0$

Solve.

$x=1$ so $x/neq 1$ in the domain.

Putting this together we get the domain is $x>1$ and we write it as $(1, \infty)$.

Exercise $\PageIndex{9}$

Find the domain of the function, $f(x)=\sqrt{\frac{4}{x+3}}$. Write the domain in interval notation.

Answer

$(-3, \infty)$

Exercise $\PageIndex{10}$

Find the domain of the function, $h(x)=\sqrt{\frac{9}{x-5}}$. Write the domain in interval notation.

Answer

$(5, \infty)$

The next example involves a cube root and so will require different thinking.

Example $\PageIndex{6}$

Find the domain of the function, $f(x)=\sqrt[3]{2 x^{2}+3}$. Write the domain in interval notation.

Solution:

Since the function, $f(x)=\sqrt[3]{2 x^{2}+3}$ has a radical with an index of $3$, which is odd, we know the radicand can be any real number. This tells us the domain is any real number. In interval notation, we write $(-\infty, \infty)$.

The domain of $f(x)=\sqrt[3]{2 x^{2}+3}$ is all real numbers and we write it in interval notation as $(-\infty, \infty)$.

Exercise $\PageIndex{11}$

Find the domain of the function, $f(x)=\sqrt[3]{3 x^{2}-1}$. Write the domain in interval notation.

Answer

$(-\infty, \infty)$

Exercise $\PageIndex{12}$

Find the domain of the function, $g(x)=\sqrt[3]{5 x-4}$. Write the domain in interval notation.

Answer

$(-\infty, \infty)$

Graph Radical Functions

Before we graph any radical function, we first find the domain of the function. For the function, $f(x)=\sqrt{x}$, the index is even, and so the radicand must be greater than or equal to $0$.

This tells us the domain is $x≥0$ and we write this in interval notation as $[0,∞)$.

Previously we used point plotting to graph the function, $f(x)=\sqrt{x}$. We chose $x$-values, substituted them in and then created a chart. Notice we chose points that are perfect squares in order to make taking the square root easier.

Figure 8.7.1

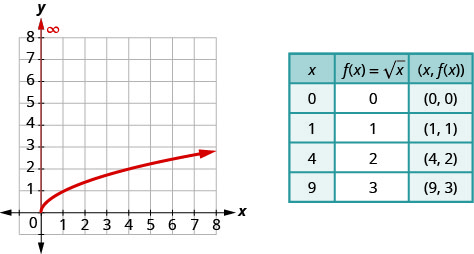
Once we see the graph, we can find the range of the function. The $y$-values of the function are greater than or equal to zero. The range then is $[0,∞)$.

Example $\PageIndex{7}$

For the function $f(x)=\sqrt{x+3}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Solution:

1. Since the radical has index $2$, we know the radicand must be greater than or equal to zero. If $x+3 \geq 0$, then $x \geq-3$. This tells us the domain is all values $x \geq-3$ and written in interval notation as $[-3, \infty)$.
2. To graph the function, we choose points in the interval $[-3, \infty)$ that will also give us a radicand which will be easy to take the square root.

Figure 8.7.2

c. Looking at the graph, we see the $y$-values of the function are greater than or equal to zero. The range then is $[0, \infty)$.

Exercise $\PageIndex{13}$

For the function $f(x)=\sqrt{x+2}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Answer

1. domain: $[-2, \infty)$
2. 
   
   Figure 8.7.3
3. range: $[0, \infty)$

Exercise $\PageIndex{14}$

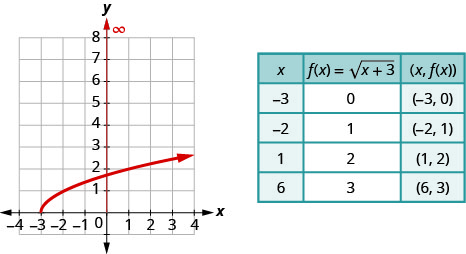
For the function $f(x)=\sqrt{x-2}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Answer

1. domain: $[2, \infty)$
2. 
   
   Figure 8.7.4
3. range: $[0, \infty)$

In our previous work graphing functions, we graphed $f(x)=x^{3}$ but we did not graph the function $f(x)=\sqrt[3]{x}$. We will do this now in the next example.

Example $\PageIndex{8}$

For the function, $f(x)=\sqrt[3]{x}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Solution:

a. Since the radical has index $3$, we know the radicand can be any real number. This tells us the domain is all real numbers and written in interval notation as $(-\infty, \infty)$

b. To graph the function, we choose points in the interval $(-\infty, \infty)$ that will also give us a radicand which will be easy to take the cube root.

Figure 8.7.5

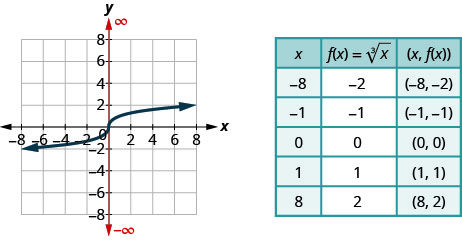
c. Looking at the graph, we see the $y$-values of the function are all real numbers. The range then is $(-\infty, \infty)$.

Exercise $\PageIndex{15}$

For the function $f(x)=-\sqrt[3]{x}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Answer

1. domain: $(-\infty, \infty)$
2. 
   
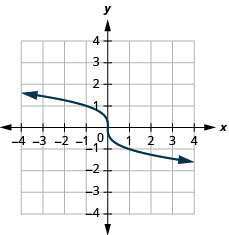
   Figure 8.7.6
3. range: $(-\infty, \infty)$

Exercise $\PageIndex{16}$

For the function $f(x)=\sqrt[3]{x-2}$,

1. find the domain
2. graph the function
3. use the graph to determine the range

Answer

1. domain: $(-\infty, \infty)$
2. 
   
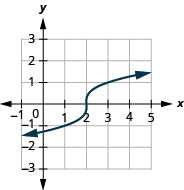
   Figure 8.7.7
3. range: $(-\infty, \infty)$

Access these online resources for additional instruction and practice with radical functions.

• Domain of a Radical Function
• Domain of a Radical Function 2
• Finding Domain of a Radical Function

Key Concepts

• Properties of $\sqrt[n]{a}$
  • When $n$ is an even number and:
    $a≥0$, then $\sqrt[n]{a}$ is a real number.
    $a<0$, then $\sqrt[n]{a}$ is not a real number.
  • When $n$ is an odd number, $\sqrt[n]{a}$ is a real number for all values of $a$.
• Domain of a Radical Function
  • When the index of the radical is even, the radicand must be greater than or equal to zero.
  • When the index of the radical is odd, the radicand can be any real number.

Glossary

radical function

A radical function is a function that is defined by a radical expression.