Skip to main content
Mathematics LibreTexts

5.3: Use Radicals in Functions

  1. Last updated
  2. Save as PDF
  • Page ID
    104850

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Learning Objectives

    By the end of this section, you will be able to:

    • Evaluate a radical function
    • Find the domain of a radical function
    • Graph radical functions
    Warm Up
    1. Solve: \(1−2x≥0\)
    2. For \(f(x)=3x−4\), evaluate \(f(2),f(−1),f(0)\)
    3. For \(f(x)=\sqrt{x}\), evaluate \(f(4),f(-1),f(0)\)
    Answer
    1. \(x\leq -\frac{1}{2}\)
    2. \(f(2)=2, f(-1)=-7, f(0)=-4\)
    3. \(f(4)=2, f(-1)=i, f(0)=0\)

    Evaluate a Radical Function

    In this section we will extend our previous work with functions to include radicals. If a function is defined by a radical expression, we call it a radical function.

    • The square root function is \(f(x)=\sqrt{x}\).
    • The cube root function is \(f(x)=\sqrt[3]{x}\).
    Definition: RADICAL FUNCTION

    A radical function is a function that is defined by a radical expression.

    We will be evaluating higher power roots but first let's review how we evaluated square roots.

    Example \(\PageIndex{1}\)

    For the function \(f(x)=\sqrt{2 x-1}\), find

    1. \(f(5)\)
    2. \(f(-2)\)

    Solution:

    a.

    \(f(x)=\sqrt{2 x-1}\)

    To evaluate \(f(5)\), substitute \(5\) for \(x\).

    \(f(5)=\sqrt{2 \cdot 5-1}\)

    Simplify.

    \(f(5)=\sqrt{9}\)

    Take the square root.

    \(f(5)=3\)

    b.

    \(f(x)=\sqrt{2 x-1}\)

    To evaluate \(f(-2)\), substitute \(-2\) for \(x\).

    \(f(-2)=\sqrt{2(-2)-1}\)

    Simplify.

    \(f(-2)=\sqrt{-5}\)

    \(f(-2)=\sqrt{5}i\)

    Exercise \(\PageIndex{2}\)

    For the function \(f(x)=\sqrt{3 x-2}\), find

    1. \(f(6)\)
    2. \(f(0)\)
    Answer
    1. \(f(6)=4\)
    2. \(f(0)=\sqrt{2}i\)
    Exercise \(\PageIndex{3}\)

    For the function \(g(x)=\sqrt{5x+5}\), find

    1. \(g(4)\)
    2. \(g(-3)\)
    Answer
    1. \(g(4)=5\)
    2. \(g(-3)=\sqrt{10}i

    We follow the same procedure to evaluate cube roots.

    Example \(\PageIndex{4}\)

    For the function \(g(x)=\sqrt[3]{x-6}\), find

    1. \(g(14)\)
    2. \(g(-2)\)

    Solution:

    a.

    \(g(x)=\sqrt[3]{x-6}\)

    To evaluate \(g(14)\), substitute \(14\) for \(x\).

    \(g(14)=\sqrt[3]{14-6}\)

    Simplify.

    \(g(14)=\sqrt[3]{8}\)

    Take the cube root.

    \(g(14)=2\)

    b.

    \(g(x)=\sqrt[3]{x-6}\)

    To evaluate \(g(-2)\), substitute \(-2\) for \(x\).

    \(g(-2)=\sqrt[3]{-2-6}\)

    Simplify.

    \(g(-2)=\sqrt[3]{-8}\)

    Take the cube root.

    \(g(-2)=-2\)

    Exercise \(\PageIndex{5}\)

    For the function \(g(x)=\sqrt[3]{3 x-4}\), find

    1. \(g(4)\)
    2. \(g(1)\)
    Answer
    1. \(g(4)=2\)
    2. \(g(1)=-1\)
    Exercise \(\PageIndex{6}\)

    For the function \(h(x)=\sqrt[3]{5 x-2}\), find

    1. \(h(2)\)
    2. \(h(-5)\)
    Answer
    1. \(h(2)=2\)
    2. \(h(-5)=-3\)

    The next example has fourth roots.

    Example \(\PageIndex{7}\)

    For the function \(f(x)=\sqrt[4]{5 x-4}\), find

    1. \(f(4)\)
    2. \(f(-12)\)

    Solution:

    a.

    \(f(x)=\sqrt[4]{5 x-4}\)

    To evaluate \(f(4)\), substitute \(4\) for \(x\).

    \(f(4)=\sqrt[4]{5 \cdot 4-4}\)

    Simplify.

    \(f(4)=\sqrt[4]{16}\)

    Take the fourth root.

    \(f(4)=2\)

    b.

    \(f(x)=\sqrt[4]{5 x-4}\)

    To evaluate \(f(-12)\), substitute \(-12\) for \(x\).

    \(f(-12)=\sqrt[4]{5(-12)-4}\)

    Simplify.

    \(f(-12)=\sqrt[4]{-64}\)

    \(f(-12)=2\sqrt[4]{4}i\)

    Exercise \(\PageIndex{8}\)

    For the function \(f(x)=\sqrt[4]{3 x+4}\), find

    1. \(f(4)\)
    2. \(f(-1)\)
    Answer
    1. \(f(4)=2\)
    2. \(f(-1)=1\)
    Exercise \(\PageIndex{9}\)

    For the function \(g(x)=\sqrt[4]{5 x+1}\), find

    1. \(g(16)\)
    2. \(g(3)\)
    Answer
    1. \(g(16)=3\)
    2. \(g(3)=2\)

    Find the Domain and Range of a Radical Function

    To find the domain and range of radical functions, we use our properties of radicals. For a radical with an even index, we said the radicand had to be greater than or equal to zero as even roots of negative numbers are not real numbers. For an odd index, the radicand can be any real number. We restate the properties here for reference.

    Properties of \(\sqrt[n]{a}\)

    When \(n\) is an even number and:

    • \(a \geq 0\), then \(\sqrt[n]{a}\) is a real number.
    • \(a<0\), then \(\sqrt[n]{a}\) is an imaginary number

    When \(n\) is an odd number, \(\sqrt[n]{a}\) is a real number for all values of \(a\).

    So, to find the domain of a radical function with even index, we set the radicand to be greater than or equal to zero. For an odd index radical, the radicand can be any real number.

    Domain of a Radical Function

    Remember, we are graphing on the real number line with output also on the real number line so there is no room on our graph for imaginary numbers. So if we get an imaginary number then it is not part of our domain for \(\sqrt[n]{a}\).

    For example, if we have \(f(x)=\sqrt{x}\), and we want to plot a point at x=4 then we would have the point \((4,2)\). If we wanted to plot a point at \(x=-1\) then we can't since that is an imaginary number and so we don't include \(x=-1\) in our domain.

    When the index of the radical is even, the radicand must be greater than or equal to zero.

    When the index of the radical is odd, the radicand can be any real number.

    Example \(\PageIndex{10}\)

    Find the domain of the function, \(f(x)=\sqrt{x}\). Write the domain in interval notation.

    Solution

    The index of \(\sqrt{x}\) is two so we must have whatever is inside the radical to be more than or equal to zero. Only x is inside the radical so \(x\geq 0\) is our domain.

    In interval notation, this is \([0,\infty)\).

    Remember we use brackets [] to include numbers and parenthesis () to exclude numbers or for \(\pm \infty\).

    Example \(\PageIndex{11}\)

    Find the domain of the function, \(f(x)=\sqrt{3 x-4}\). Write the domain in interval notation.

    Solution:

    Since the function, \(f(x)=\sqrt{3 x-4}\) has a radical with an index of \(2\), which is even, we know the radicand must be greater than or equal to \(0\). We set the radicand to be greater than or equal to \(0\) and then solve to find the domain.

    Solve.

    \(\begin{aligned} 3 x-4 & \geq 0 \\ 3 x & \geq 4 \\ x & \geq \frac{4}{3} \end{aligned}\)

    The domain of \(f(x)=\sqrt{3 x-4}\) is all values \(x \geq \frac{4}{3}\) and we write it in interval notation as \(\left[\frac{4}{3}, \infty\right)\).

    Exercise \(\PageIndex{12}\)

    Find the domain of the function, \(f(x)=\sqrt{6 x-5}\). Write the domain in interval notation.

    Answer

    \(\left[\frac{5}{6}, \infty\right)\)

    Exercise \(\PageIndex{13}\)

    Find the domain of the function, \(f(x)=\sqrt{4-5 x}\). Write the domain in interval notation.

    Answer

    Domain: \(\left(-\infty, \frac{4}{5}\right]\)

    Graph Radical Functions

    Before we graph any radical function, we first find the domain of the function. For the function, \(f(x)=\sqrt{x}\), the index is even, and so the radicand must be greater than or equal to \(0\).

    This tells us the domain is \(x≥0\) and we write this in interval notation as \([0,∞)\).

    Previously we used point plotting to graph the function, \(f(x)=\sqrt{x}\). We chose \(x\)-values, substituted them in and then created a chart. Notice we chose points that are perfect squares in order to make taking the square root easier.

    The figure shows the square root function graph on the x y-coordinate plane. The x-axis of the plane runs from 0 to 7. The y-axis runs from 0 to 7. The function has a starting point at (0, 0) and goes through the points (1, 1) and (4, 2). A table is shown beside the graph with 3 columns and 5 rows. The first row is a header row with the expressions “x”, “f (x) = square root of x”, and “(x, f (x))”. The second row has the numbers 0, 0, and (0, 0). The third row has the numbers 1, 1, and (1, 1). The fourth row has the numbers 4, 2, and (4, 2). The fifth row has the numbers 9, 3, and (9, 3).
    Figure 8.7.1

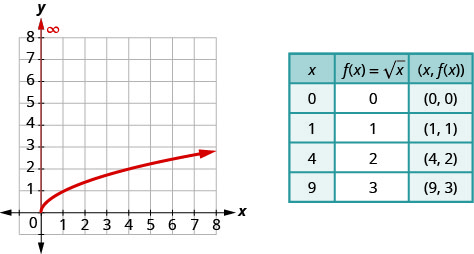
    Once we see the graph, we can find the range of the function. The \(y\)-values of the function are greater than or equal to zero. The range then is \([0,∞)\).

    Example \(\PageIndex{14}\)

    For the function \(f(x)=\sqrt{x+3}\),

    1. find the domain and range
    2. graph the function
    3. use the graph to determine the range

    Solution:

    1. Since the radical has index \(2\), we know the radicand must be greater than or equal to zero. If \(x+3 \geq 0\), then \(x \geq-3\). This tells us the domain is all values \(x \geq-3\) and written in interval notation as \([-3, \infty)\). While the range is \([0,\infty)\) since \(f(-3)=0\) and as x grows to \(\infty\), \(f(x)\) grows to \(\infty\).
    2. To graph the function, we choose points in the interval \([-3, \infty)\) that will also give us a radicand which will be easy to take the square root.
    The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 3 to 3. The y-axis runs from 0 to 7. The function has a starting point at (negative 3, 0) and goes through the points (negative 2, 1) and (1, 2). A table is shown beside the graph with 3 columns and 5 rows. The first row is a header row with the expressions “x”, “f (x) = square root of the quantity x plus 3”, and “(x, f (x))”. The second row has the numbers negative 3, 0, and (negative 3, 0). The third row has the numbers negative 2, 1, and (negative 2, 1). The fourth row has the numbers 1, 2, and (1, 2). The fifth row has the numbers 6, 3, and (6, 3).
    Figure 8.7.2

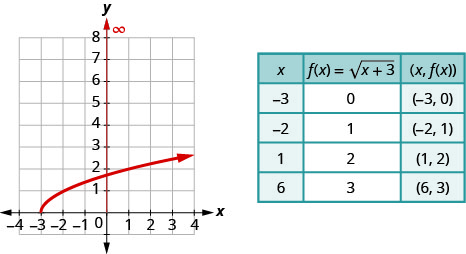
    c. Looking at the graph, we see the \(y\)-values of the function are greater than or equal to zero. The range then is \([0, \infty)\).

    Exercise \(\PageIndex{15}\)

    For the function \(f(x)=\sqrt{x+2}\),

    1. find the domain and range
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \([-2, \infty)\)

    range: \([0,\infty\)


    1. The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 2 to 6. The y-axis runs from 0 to 8. The function has a starting point at (negative 2, 0) and goes through the points (negative 1, 1) and (2, 2).
      Figure 8.7.3
    2. range: \([0, \infty)\)
    Exercise \(\PageIndex{16}\)

    For the function \(f(x)=\sqrt{x-2}\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \([2, \infty)\)

    2. The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from 0 to 8. The y-axis runs from 0 to 6. The function has a starting point at (2, 0) and goes through the points (3, 1) and (6, 2).
      Figure 8.7.4
    3. range: \([0, \infty)\)

    We notice a pattern here. If we add a positive number to x inside the radical, then the graph moves to the left by that number. This is because we shifted the x values by that number. Likewise, if we subtract a positive number from x inside the radical, then the graph moves to the right by that number.

    What happens when we add a positive number outside the radical?

    Exercise \(\PageIndex{17}\)

    For the function \(f(x)=\sqrt{x}+2\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \([0,\infty\)
    2.  

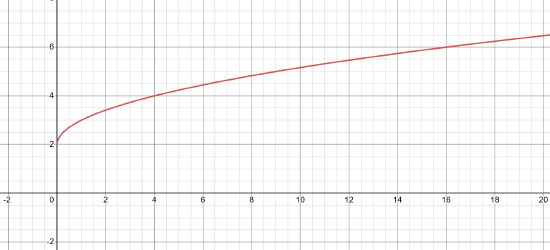
    sqrt{x}+2.png

    1. Range: \([2,\infty\)

    What about if we subtract?

    Exercise \(\PageIndex{18}\)

    For the function \(f(x)=\sqrt{x}+2\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \([0,\infty\)
    2.  

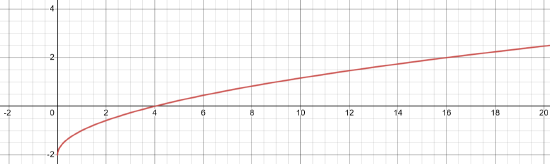
    sqrt{x}-2.png

    1. Range: \([-2,\infty\)

    So adding or subtracting a positive number outside the radical makes the function go up or down in accordance to that number.

    We can also do add or subtract a number inside and outside to make it move left/right and up/down.

    In our previous work graphing functions, we graphed \(f(x)=x^{3}\) but we did not graph the function \(f(x)=\sqrt[3]{x}\). We will do this now in the next example.

    Example \(\PageIndex{19}\)

    For the function, \(f(x)=\sqrt[3]{x}\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range

    Solution:

    a. Since the radical has index \(3\), we know the radicand can be any real number. This tells us the domain is all real numbers and written in interval notation as \((-\infty, \infty)\)

    b. To graph the function, we choose points in the interval \((-\infty, \infty)\) that will also give us a radicand which will be easy to take the cube root.

    The figure shows the cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The function has a center point at (0, 0) and goes through the points (1, 1), (negative 1, negative 1), (8, 2), and (negative 8, negative 2). A table is shown beside the graph with 3 columns and 6 rows. The first row is a header row with the expressions “x”, “f (x) = cube root of x”, and “(x, f (x))”. The second row has the numbers negative 8, negative 2, and (negative 8, negative 2). The third row has the numbers negative 1, negative 1, and (negative 1, negative 1). The fourth row has the numbers 0, 0, and (0, 0). The fifth row has the numbers 1, 1, and (1, 1). The sixth row has the numbers 8, 2, and (8, 2).
    Figure 8.7.5

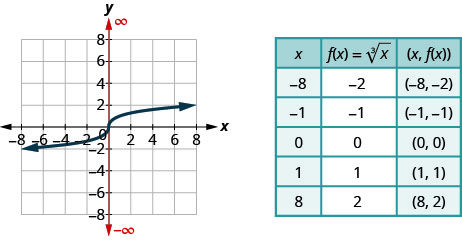
    c. Looking at the graph, we see the \(y\)-values of the function are all real numbers. The range then is \((-\infty, \infty)\).

    Exercise \(\PageIndex{20}\)

    For the function \(f(x)=-\sqrt[3]{x}\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \((-\infty, \infty)\)

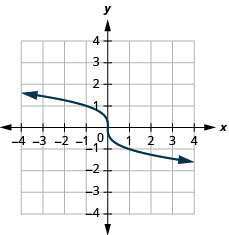
    2. The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 2 to 2. The y-axis runs from negative 2 to 2. The function has a center point at (0, 0) and goes through the points (1, negative 1) and (negative 1, 1).
      Figure 8.7.6
    3. range: \((-\infty, \infty)\)
    Exercise \(\PageIndex{21}\)

    For the function \(f(x)=\sqrt[3]{x-2}\),

    1. find the domain
    2. graph the function
    3. use the graph to determine the range
    Answer
    1. domain: \((-\infty, \infty)\)

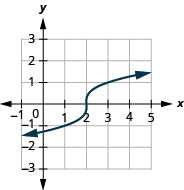
    2. The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 1 to 5. The y-axis runs from negative 3 to 3. The function has a center point at (2, 0) and goes through the points (1, negative 1) and (3, 2).
      Figure 8.7.7
    3. range: \((-\infty, \infty)\)

    Key Concepts

    • Properties of \(\sqrt[n]{a}\)
      • When \(n\) is an even number and:
        \(a≥0\), then \(\sqrt[n]{a}\) is a real number.
        \(a<0\), then \(\sqrt[n]{a}\) is not a real number.
      • When \(n\) is an odd number, \(\sqrt[n]{a}\) is a real number for all values of \(a\).
    • Domain of a Radical Function
      • When the index of the radical is even, the radicand must be greater than or equal to zero.
      • When the index of the radical is odd, the radicand can be any real number.

    Glossary

    radical function
    A radical function is a function that is defined by a radical expression.

    This page titled 5.3: Use Radicals in Functions is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Stanislav A. Trunov and Elizabeth J. Hale via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.