9.3: Geometric Sequences and Series

Learning Objectives

• Identify the common ratio of a geometric sequence.
• Find a formula for the general term of a geometric sequence.
• Calculate the \(n\)th partial sum of a geometric sequence.
• Calculate the sum of an infinite geometric series when it exists.

Geometric Sequences

A geometric sequence¹⁸, or geometric progression¹⁹, is a sequence of numbers where each successive number is the product of the previous number and some constant \(r\).

\(a_{n}=r a_{n-1} \quad\color{Cerulean}{Geometric\:Sequence}\)

And because \(\frac{a_{n}}{a_{n-1}}=r\), the constant factor \(r\) is called the common ratio²⁰. For example, the following is a geometric sequence,

\(9,27,81,243,729 \ldots\)

Here \(a_{1} = 9\) and the ratio between any two successive terms is \(3\). We can construct the general term \(a_{n}=3 a_{n-1}\) where,

\(\begin{aligned} a_{1} &=9 \\ a_{2} &=3 a_{1}=3(9)=27 \\ a_{3} &=3 a_{2}=3(27)=81 \\ a_{4} &=3 a_{3}=3(81)=243 \\ a_{5} &=3 a_{4}=3(243)=729 \\ & \vdots \end{aligned}\)

In general, given the first term \(a_{1}\) and the common ratio \(r\) of a geometric sequence we can write the following:

\(\begin{aligned} a_{2} &=r a_{1} \\ a_{3} &=r a_{2}=r\left(a_{1} r\right)=a_{1} r^{2} \\ a_{4} &=r a_{3}=r\left(a_{1} r^{2}\right)=a_{1} r^{3} \\ a_{5} &=r a_{3}=r\left(a_{1} r^{3}\right)=a_{1} r^{4} \\ & \vdots \end{aligned}\)

From this we see that any geometric sequence can be written in terms of its first element, its common ratio, and the index as follows:

\(a_{n}=a_{1} r^{n-1} \quad\color{Cerulean}{Geometric\:Sequence}\)

In fact, any general term that is exponential in \(n\) is a geometric sequence.

Example \(\PageIndex{1}\):

Find an equation for the general term of the given geometric sequence and use it to calculate its \(10^{th}\) term: \(3, 6, 12, 24, 48…\)

Solution

Begin by finding the common ratio,

\(r=\frac{6}{3}=2\)

Note that the ratio between any two successive terms is \(2\). The sequence is indeed a geometric progression where \(a_{1} = 3\) and \(r = 2\).

\(\begin{aligned} a_{n} &=a_{1} r^{n-1} \\ &=3(2)^{n-1} \end{aligned}\)

Therefore, we can write the general term \(a_{n}=3(2)^{n-1}\) and the \(10^{th}\) term can be calculated as follows:

\(\begin{aligned} a_{10} &=3(2)^{10-1} \\ &=3(2)^{9} \\ &=1,536 \end{aligned}\)

Answer:

\(a_{n}=3(2)^{n-1} ; a_{10}=1,536\)

The terms between given terms of a geometric sequence are called geometric means²¹.

Example \(\PageIndex{2}\):

Find all terms between \(a_{1} = −5\) and \(a_{4} = −135\) of a geometric sequence. In other words, find all geometric means between the \(1^{st}\) and \(4^{th}\) terms.

Solution

Begin by finding the common ratio \(r\). In this case, we are given the first and fourth terms:

\(\begin{aligned} a_{n} &=a_{1} r^{n-1} \quad\color{Cerulean} { Use \: n=4} \\ a_{4} &=a_{1} r^{4-1} \\ a_{4} &=a_{1} r^{3} \end{aligned}\)

Substitute \(a_{1} = −5\) and \(a_{4} = −135\) into the above equation and then solve for \(r\).

\(\begin{aligned}-135 &=-5 r^{3} \\ 27 &=r^{3} \\ 3 &=r \end{aligned}\)

Next use the first term \(a_{1} = −5\) and the common ratio \(r = 3\) to find an equation for the \(n\)th term of the sequence.

\(\begin{aligned} a_{n} &=a_{1} r^{n-1} \\ a_{n} &=-5(3)^{n-1} \end{aligned}\)

Now we can use \(a_{n}=-5(3)^{n-1}\) where \(n\) is a positive integer to determine the missing terms.

\(\left.\begin{array}{l}{a_{1}=-5(3)^{1-1}=-5 \cdot 3^{0}=-5} \\ {a_{2}=-5(3)^{2-1}=-5 \cdot 3^{1}=-15} \\ {a_{3}=-5(3)^{3-1}=-5 \cdot 3^{2}=-45} \\ a_{4}=-5(3)^{4-1}=-5\cdot3^{3}=-135\end{array}\right\} \color{Cerulean}{geometric\:means}\)

Answer:

\(-15,-45\)

The first term of a geometric sequence may not be given.

Example \(\PageIndex{3}\):

Find the general term of a geometric sequence where \(a_{2} = −2\) and \(a_{5}=\frac{2}{125}\).

Solution

To determine a formula for the general term we need \(a_{1}\) and \(r\). A nonlinear system with these as variables can be formed using the given information and \(a_{n}=a_{1} r^{n-1} :\):

\(\left\{\begin{array}{l}{a_{2}=a_{1} r^{2-1}} \\ {a_{5}=a_{1} r^{5-1}}\end{array}\right. \Longrightarrow \left\{\begin{array}{l}{-2=a_{1} r \quad\:\:\:\color{Cerulean}{Use\:a_{2}=-2.}} \\ {\frac{2}{125}=a_{1} r^{4} \quad\color{Cerulean}{Use\:a_{5}=\frac{2}{125}.}}\end{array}\right.\)

Solve for \(a_{1}\) in the first equation,

\(-2=a_{1} r \quad \Rightarrow \quad \frac{-2}{r}=a_{1}\)
\(\frac{2}{125}=a_{1} r^{4}\)

Substitute \(a_{1} = \frac{-2}{r}\) into the second equation and solve for \(r\).

\(\frac{2}{125}=a_{1} r^{4}\)
\(\frac{2}{125}=\left(\frac{-2}{r}\right) r^{4}\)
\(\frac{2}{125}=-2 r^{3}\)
\(-\frac{1}{125}=r^{3}\)
\(-\frac{1}{5}=r\)

Back substitute to find \(a_{1}\):

\(\begin{aligned} a_{1} &=\frac{-2}{r} \\ &=\frac{-2}{\left(-\frac{1}{5}\right)} \\ &=10 \end{aligned}\)

Therefore, \(a_{1} = 10\) and \(r = −\frac{1}{5}\).

Answer:

\(a_{n}=10\left(-\frac{1}{5}\right)^{n-1}\)

Exercise \(\PageIndex{1}\)

Find an equation for the general term of the given geometric sequence and use it to calculate its \(6^{th}\) term: \(2, \frac{4}{3},\frac{8}{9}, …\)

Answer

\(a_{n}=2\left(\frac{2}{3}\right)^{n-1} ; a_{6}=\frac{64}{243}\)

www.youtube.com/v/IGPEl9vloLY

Geometric Series

A geometric series²² is the sum of the terms of a geometric sequence. For example, the sum of the first \(5\) terms of the geometric sequence defined by \(a_{n}=3^{n+1}\) follows:

\(\begin{aligned} S_{5} &=\sum_{n=1}^{5} 3^{n+1} \\ &=3^{1+1}+3^{2+1}+3^{3+1}+3^{4+1}+3^{5+1} \\ &=3^{2}+3^{3}+3^{4}+3^{5}+3^{6} \\ &=9+27+81+3^{5}+3^{6} \\ &=1,089 \end{aligned}\)

Adding \(5\) positive integers is manageable. However, the task of adding a large number of terms is not. Therefore, we next develop a formula that can be used to calculate the sum of the first \(n\) terms of any geometric sequence. In general,

\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)

Multiplying both sides by \(r\) we can write,

\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)

Subtracting these two equations we then obtain,

\(S_{n}-r S_{n}=a_{1}-a_{1} r^{n}\)
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)

Assuming \(r ≠ 1\) dividing both sides by \((1 − r)\) leads us to the formula for the \(n\)th partial sum of a geometric sequence²³:

\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}(r \neq 1)\)

In other words, the \(n\)th partial sum of any geometric sequence can be calculated using the first term and the common ratio. For example, to calculate the sum of the first \(15\) terms of the geometric sequence defined by \(a_{n}=3^{n+1}\), use the formula with \(a_{1} = 9\) and \(r = 3\).

\(\begin{aligned} S_{15} &=\frac{a_{1}\left(1-r^{15}\right)}{1-r} \\ &=\frac{9 \cdot\left(1-3^{15}\right)}{1-3} \\ &=\frac{9(-14,348,906)}{-2} \\ &=64,570,077 \end{aligned}\)

Example \(\PageIndex{4}\):

Find the sum of the first 10 terms of the given sequence: \(4, −8, 16, −32, 64,… \)

Solution

Determine whether or not there is a common ratio between the given terms.

\(r=\frac{-8}{4}=-2\)

Note that the ratio between any two successive terms is \(−2\); hence, the given sequence is a geometric sequence. Use \(r = −2\) and the fact that \(a_{1} = 4\) to calculate the sum of the first \(10\) terms,

\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S_{10} &=\frac{\color{Cerulean}{4}\color{black}{\left[1-(\color{Cerulean}{-2}\color{black}{)}^{10}\right]}}{1-(\color{Cerulean}{-2}\color{black}{)}} ] \\ &=\frac{4(1-1,024)}{1+2} \\ &=\frac{4(-1,023)}{3} \\ &=-1,364 \end{aligned}\)

Answer:

\(S_{10}=-1,364\)

Example \(\PageIndex{5}\):

Evaluate: \(\sum_{n=1}^{6} 2(-5)^{n}\).

Solution

In this case, we are asked to find the sum of the first \(6\) terms of a geometric sequence with general term \(a_{n} = 2(−5)^{n}\). Use this to determine the \(1^{st}\) term and the common ratio \(r\):

\(a_{1}=2(-5)^{1}=-10\)

To show that there is a common ratio we can use successive terms in general as follows:

\(\begin{aligned} r &=\frac{a_{n}}{a_{n-1}} \\ &=\frac{2(-5)^{n}}{2(-5)^{n-1}} \\ &=(-5)^{n-(n-1)} \\ &=(-5)^{1}\\&=-5 \end{aligned}\)

Use \(a_{1} = −10\) and \(r = −5\) to calculate the \(6^{th}\) partial sum.

\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S_{6} &=\frac{\color{Cerulean}{-10}\color{black}{\left[1-(\color{Cerulean}{-5}\color{black}{)}^{6}\right]}}{1-(\color{Cerulean}{-5}\color{black}{)}} \\ &=\frac{-10(1-15,625)}{1+5} \\ &=\frac{-10(-15,624)}{6} \\ &=26,040 \end{aligned}\)

Answer:

\(26,040\)

Exercise \(\PageIndex{2}\)

Find the sum of the first 9 terms of the given sequence: \(-2,1,-1 / 2, \dots\)

Answer

\(S_{9}=-\frac{171}{128}\)

www.youtube.com/v/v-t3P95rWe8

If the common ratio r of an infinite geometric sequence is a fraction where \(|r| < 1\) (that is \(−1 < r < 1\)), then the factor \((1 − r^{n})\) found in the formula for the \(n\)th partial sum tends toward \(1\) as \(n\) increases. For example, if \(r = \frac{1}{10}\) and \(n = 2, 4, 6\) we have,

\(1-\left(\frac{1}{10}\right)^{2}=1-0.01=0.99\)
\(1-\left(\frac{1}{10}\right)^{4}=1-0.0001=0.9999\)
\(1-\left(\frac{1}{10}\right)^{6}=1-0.00001=0.999999\)

Here we can see that this factor gets closer and closer to 1 for increasingly larger values of \(n\). This illustrates the idea of a limit, an important concept used extensively in higher-level mathematics, which is expressed using the following notation:

\(\lim _{n \rightarrow \infty}\left(1-r^{n}\right)=1\) where \(|r|<1\)

This is read, “the limit of \((1 − r^{n})\) as \(n\) approaches infinity equals \(1\).” While this gives a preview of what is to come in your continuing study of mathematics, at this point we are concerned with developing a formula for special infinite geometric series. Consider the \(n\)th partial sum of any geometric sequence,

\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}=\frac{a_{1}}{1-r}\left(1-r^{n}\right)\)

If \(|r| < 1\) then the limit of the partial sums as n approaches infinity exists and we can write,

\(S_{n}=\frac{a_{1}}{1-r}\left(1-r^{n}\right)\quad\color{Cerulean}{\stackrel{\Longrightarrow}{n\rightarrow \infty }} \quad \color{black}{S_{\infty}}=\frac{a_{1}}{1-4}\cdot1\)

Therefore, a convergent geometric series²⁴ is an infinite geometric series where \(|r| < 1\); its sum can be calculated using the formula:

\(S_{\infty}=\frac{a_{1}}{1-r}\)

Example \(\PageIndex{6}\):

Find the sum of the infinite geometric series: \(\frac{3}{2}+\frac{1}{2}+\frac{1}{6}+\frac{1}{18}+\frac{1}{54}+\dots\)

Solution

Determine the common ratio, Since the common ratio \(r = \frac{1}{3}\) is a fraction between \(−1\) and \(1\), this is a convergent geometric series. Use the first term \(a_{1} = \frac{3}{2}\) and the common ratio to calculate its sum

\(\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{\frac{3}{2}}{1-\left(\frac{1}{3}\right)} \\ &=\frac{\frac{3}{3}}{\frac{2}{3}} \\ &=\frac{3}{2} \cdot \frac{3}{2} \\ &=\frac{9}{4} \end{aligned}\)

Answer:

\(S_{\infty}=\frac{9}{4}\)

Note

In the case of an infinite geometric series where \(|r| ≥ 1\), the series diverges and we say that there is no sum. For example, if \(a_{n} = (5)^{n−1}\) then \(r = 5\) and we have

\(S_{\infty}=\sum_{n=1}^{\infty}(5)^{n-1}=1+5+25+\cdots\)

We can see that this sum grows without bound and has no sum.

Exercise \(\PageIndex{3}\)

Find the sum of the infinite geometric series: \(\sum_{n=1}^{\infty}-2\left(\frac{5}{9}\right)^{n-1}\)

Answer

\(-\frac{9}{2}\)

www.youtube.com/v/KxsPVUyle_A

A repeating decimal can be written as an infinite geometric series whose common ratio is a power of \(1/10\). Therefore, the formula for a convergent geometric series can be used to convert a repeating decimal into a fraction.

Example \(\PageIndex{7}\):

Write as a fraction: \(1.181818… \)

Solution

Begin by identifying the repeating digits to the right of the decimal and rewrite it as a geometric progression.

\(\begin{aligned} 0.181818 \ldots &=0.18+0.0018+0.000018+\ldots \\ &=\frac{18}{100}+\frac{18}{10,000}+\frac{18}{1,000,000}+\ldots \end{aligned}\)

In this form we can determine the common ratio,

\(\begin{aligned} r &=\frac{\frac{18}{10,000}}{\frac{18}{100}} \\ &=\frac{18}{10,000} \times \frac{100}{18} \\ &=\frac{1}{100} \end{aligned}\)

Note that the ratio between any two successive terms is \(\frac{1}{100}\). Use this and the fact that \(a_{1} = \frac{18}{100}\) to calculate the infinite sum:

\(\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{\frac{18}{100}}{1-\left(\frac{1}{100}\right)} \\ &=\frac{\frac{18}{100}}{\frac{90}{100}} \\ &=\frac{18}{100} \cdot \frac{100}{99} \\ &=\frac{2}{11} \end{aligned}\)

Therefore, \(0.181818… = \frac{2}{11}\) and we have,

\(1.181818 \ldots=1+\frac{2}{11}=1 \frac{2}{11}\)

Answer:

\(1 \frac{2}{11}\)

Example \(\PageIndex{8}\):

A certain ball bounces back to two-thirds of the height it fell from. If this ball is initially dropped from \(27\) feet, approximate the total distance the ball travels.

Solution

We can calculate the height of each successive bounce:

\(\begin{array}{l}{27 \cdot \frac{2}{3}=18 \text { feet } \quad \color{Cerulean} { Height\: of\: the\: first\: bounce }} \\ {18 \cdot \frac{2}{3}=12 \text { feet}\quad\:\color{Cerulean}{ Height \:of\: the\: second\: bounce }} \\ {12 \cdot \frac{2}{3}=8 \text { feet } \quad\:\: \color{Cerulean} { Height\: of\: the\: third\: bounce }}\end{array}\)

Figure \(\PageIndex{1}\)

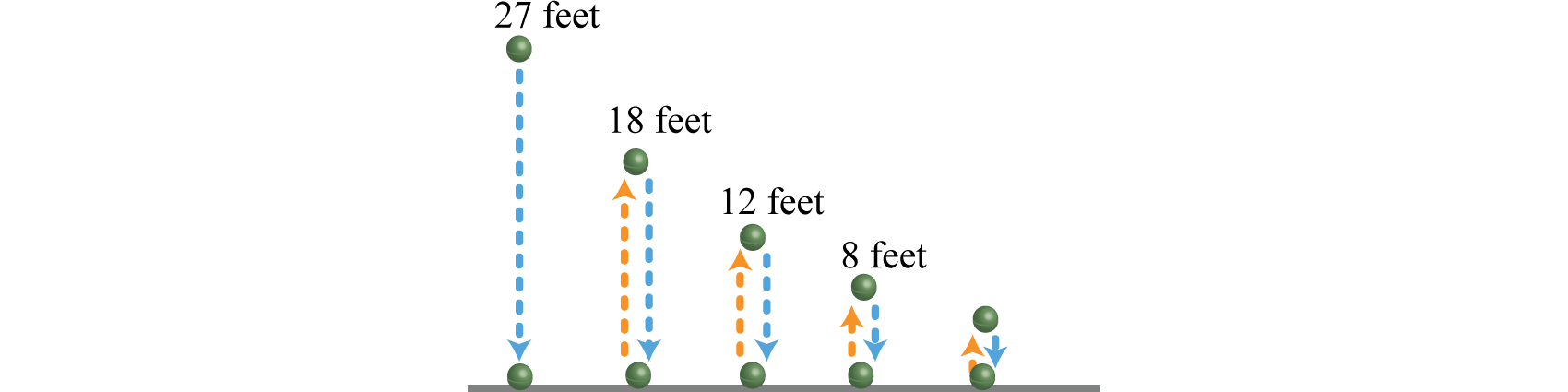
The total distance that the ball travels is the sum of the distances the ball is falling and the distances the ball is rising. The distances the ball falls forms a geometric series,

\(27+18+12+\dots \quad\color{Cerulean}{Distance\:the\:ball\:is\:falling}\)

where \(a_{1} = 27\) and \(r = \frac{2}{3}\). Because \(r\) is a fraction between \(−1\) and \(1\), this sum can be calculated as follows:

\(\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{27}{1-\frac{2}{3}} \\ &=\frac{27}{\frac{1}{3}} \\ &=81 \end{aligned}\)

Therefore, the ball is falling a total distance of \(81\) feet. The distances the ball rises forms a geometric series,

\(18+12+8+\cdots \quad\color{Cerulean}{Distance\:the\:ball\:is\:rising}\)

where \(a_{1} = 18\) and \(r = \frac{2}{3}\). Calculate this sum in a similar manner:

\(\begin{aligned} S_{\infty} &=\frac{a_{1}}{1-r} \\ &=\frac{18}{1-\frac{2}{3}} \\ &=\frac{18}{\frac{1}{3}} \\ &=54 \end{aligned}\)

Therefore, the ball is rising a total distance of \(54\) feet. Approximate the total distance traveled by adding the total rising and falling distances:

\(81+54=135\) feet

Answer:

\(135\) feet

Key Takeaways

• A geometric sequence is a sequence where the ratio \(r\) between successive terms is constant.
• The general term of a geometric sequence can be written in terms of its first term \(a_{1}\), common ratio \(r\), and index \(n\) as follows: \(a_{n} = a_{1} r^{n−1}\).
• A geometric series is the sum of the terms of a geometric sequence.
• The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and common ratio \(r\) as follows: \(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\).
• The infinite sum of a geometric sequence can be calculated if the common ratio is a fraction between \(−1\) and \(1\) (that is \(|r| < 1\)) as follows: \(S_{\infty}=\frac{a_{1}}{1-r}\). If \(|r| ≥ 1\), then no sum exists.

Footnotes

¹⁸A sequence of numbers where each successive number is the product of the previous number and some constant \(r\).

¹⁹Used when referring to a geometric sequence.

²⁰The constant \(r\) that is obtained from dividing any two successive terms of a geometric sequence; \(\frac{a_{n}}{a_{n-1}}=r\).

²¹The terms between given terms of a geometric sequence.

²²The sum of the terms of a geometric sequence.

²³The sum of the first n terms of a geometric sequence, given by the formula: \(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r} , r\neq 1\).

²⁴An infinite geometric series where \(|r| < 1\) whose sum is given by the formula:\(S_{\infty}=\frac{a_{1}}{1-r}\).