2.1: Basic Geometric Concepts

Learning Objectives

• Identify and define points, lines, line segments, rays, and planes.
• Classify angles as acute, right, obtuse, or straight.

Introduction

You use geometric terms in everyday language, often without thinking about it. For example, any time you say “walk along this line” or “watch out, this road quickly angles to the left” you are using geometric terms to make sense of the environment around you. You use these terms flexibly, and people generally know what you are talking about.

In the world of mathematics, each of these geometric terms has a specific definition. It is important to know these definitions, as well as how different figures are constructed, to become familiar with the language of geometry. Let’s start with a basic geometric figure: the plane.

Figures on a Plane

A plane is a flat surface that continues forever (or, in mathematical terms, infinitely) in every direction. It has two dimensions: length and width.

You can visualize a plane by placing a piece of paper on a table. Now imagine that the piece of paper stays perfectly flat and extends as far as you can see in two directions, left-to-right and front-to-back. This gigantic piece of paper gives you a sense of what a geometric plane is like: it continues infinitely in two directions. (Unlike the piece of paper example, though, a geometric plane has no height.)

A plane can contain a number of geometric figures. The most basic geometric idea is a point, which has no dimensions. A point is simply a location on the plane. It is represented by a dot. Three points that don’t lie in a straight line will determine a plane.

The image below shows four points, labeled A, B, C, and D.

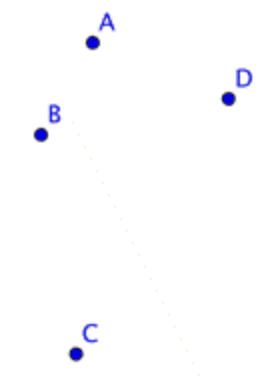
Two points on a plane determine a line. A line is a one-dimensional figure that is made up of an infinite number of individual points placed side by side. In geometry, all lines are assumed to be straight; if they bend, they are called a curve. A line continues infinitely in two directions.

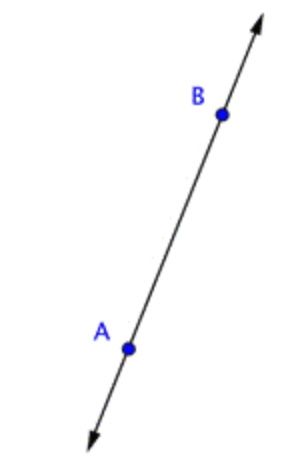
Below is \(\ \text{line} \, A B\) or, in geometric notation, \(\ \overleftrightarrow{A B}\). The arrows indicate that the line keeps going forever in the two directions. This line could also be called \(\ \text{line} \, BA\). While the order of the points does not matter for a line, it is customary to name the two points in alphabetical order.

The image below shows the points \(\ A\) and \(\ B\) and the line \(\ \overleftrightarrow{A B}\).

Example \(\PageIndex{1}\)

Name the line shown in red.

Solution

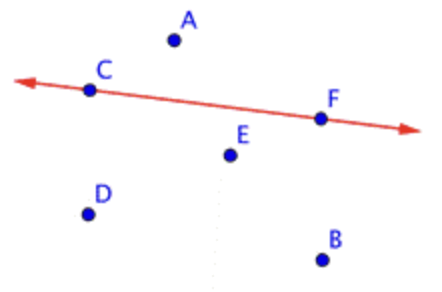The red line goes through the points \(\ C\) and \(\ F\), so the line is \(\ \overleftrightarrow{C F}\).

Line: \(\ \overleftrightarrow{C F}\)

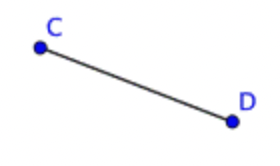
There are two more figures to consider. The section between any two points on a line is called a line segment. A line segment can be very long, very short, or somewhere in between. The difference between a line and a line segment is that the line segment has two endpoints and a line goes on forever. A line segment is denoted by its two endpoints, as in \(\ \overline{C D}\).

A ray has one endpoint and goes on forever in one direction. Mathematicians name a ray with notation like \(\ \overrightarrow{E F}\), where point \(\ E\) is the endpoint and \(\ F\) is another point on the ray. When naming a ray, we always say the endpoint first. Note that \(\ \overrightarrow{F E}\) would have the endpoint at \(\ F\), and continue through \(\ E\), which is a different ray than \(\ \overrightarrow{E F}\), which would have a endpoint at \(\ E\), and continue through \(\ F\).

The term “ray” may be familiar because it is a common word in English. “Ray” is often used when talking about light. While a ray of light resembles the geometric term “ray,” it does not go on forever, and it has some width. A geometric ray has no width; only length.

Below is an image of ray \(\ E F\) or \(\ \overrightarrow{E F}\). Notice that the endpoint is \(\ E\).

Example \(\PageIndex{2}\)

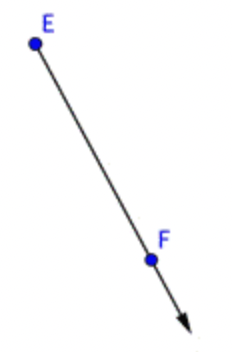
Identify each line and line segment in the picture below.

Solution

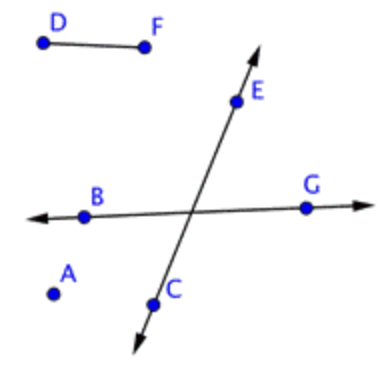Two points define a line, and a line is denoted with arrows. There are two lines in this picture: \(\ \overleftrightarrow{C E}\) and \(\ \overleftrightarrow{B G}\). A line segment is a section between two points. \(\ \overline{D F}\) is a line segment. But there are also two more line segments on the lines themselves: \(\ \overline{C E}\) and \(\ \overline{B G}\).

Lines: \(\ \overleftrightarrow{C E}, \overleftrightarrow{B G}\)

Line segments: \(\ \overline{D F}, \overline{C E}, \overline{B G}\)

Example \(\PageIndex{3}\)

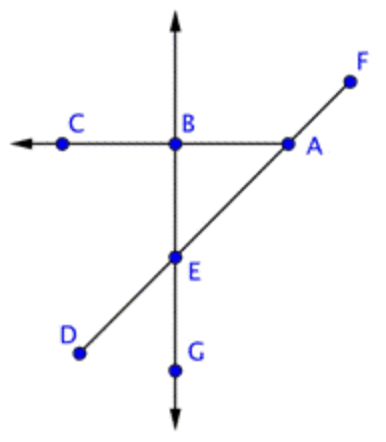
Identify each point and ray in the picture below.

Solution

There are four points: \(\ A, B, C \text{ and } D\). There are also three rays, though only one may be obvious. Ray \(\ \overrightarrow{B C}\) begins at point \( B\) and goes through \(\ C\). Two more rays exist on line \(\ \overleftrightarrow{A D}\): they are \(\ \overrightarrow{D A}\) and \(\ \overrightarrow{A D}\).

Points: \(\ A, B, C, D\)

Rays: \(\ \overrightarrow{B C}, \overrightarrow{A D}, \overrightarrow{D A}\)

Try It \(\PageIndex{1}\)

Which of the following is not represented in the image below?

1. \(\ \overleftrightarrow{B G}\)
2. \(\ \overrightarrow{B A}\)
3. \(\ \overline{D F}\)
4. \(\ \overrightarrow{A C}\)

Answer

B. This image does not show any ray that begins at point \(\ B\) and goes through point \(\ A\).

Angles

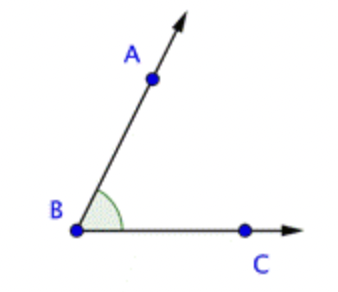
Lines, line segments, points, and rays are the building blocks of other figures. For example, two rays with a common endpoint make up an angle. The common endpoint of the angle is called the vertex.

The angle \(\ A B C\) is shown below. This angle can also be called \(\ \angle A B C\), \(\ \angle C B A\), or simply \(\ \angle B\). When you are naming angles, be careful to include the vertex (here, point \(\ B\)) as the middle letter.

The image below shows a few angles on a plane. Notice that the label of each angle is written “point-vertex-point,” and the geometric notation is in the form \(\ \angle A B C\).

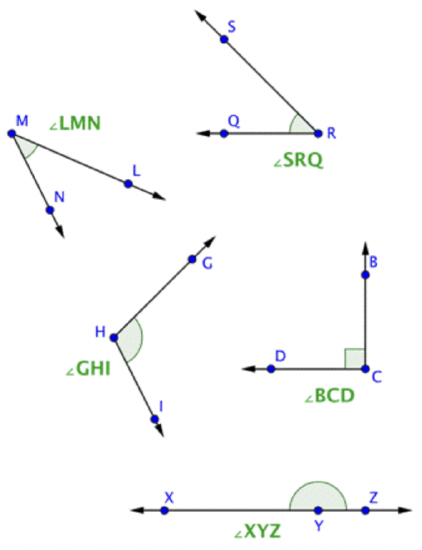
Sometimes angles are very narrow; sometimes they are very wide. When people talk about the “size” of an angle, they are referring to the arc between the two rays. The length of the rays has nothing to do with the size of the angle itself. Drawings of angles will often include an arc (as shown above) to help the reader identify the correct ‘side’ of the angle.

Think about an analog clock face. The minute and hour hands are both fixed at a point in the middle of the clock. As time passes, the hands rotate around the fixed point, making larger and smaller angles as they go. The length of the hands does not impact the angle that is made by the hands.

An angle is measured in degrees, represented by the degree symbol, which is a small circle at the upper right of a number. For example, a circle is defined as having 360°. (In skateboarding and basketball, “doing a 360" refers to jumping and doing one complete body rotation.)

A right angle is any degree that measures exactly 90°. This represents exactly one-quarter of the way around a circle. Rectangles contain exactly four right angles. A corner mark is often used to denote a right angle, as shown in right angle \(\ D C B\) below.

Angles that are between 0° and 90° (smaller than right angles) are called acute angles. Angles that are between 90° and 180° (larger than right angles and less than 180°) are called obtuse angles. And an angle that measures exactly 180° is called a straight angle because it forms a straight line!

Example \(\PageIndex{4}\)

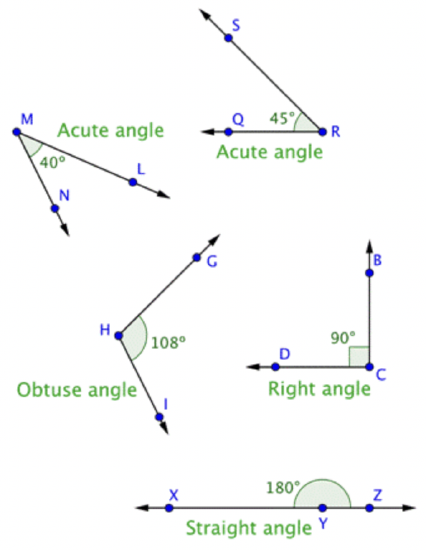
Label each angle below as acute, right, or obtuse.

Solution

You can start by identifying any right angles. \(\ \angle G F I\) is a right angle, as indicated by the corner mark at vertex \(\ F\). Acute angles will be smaller than \(\ \angle G F I\) (or less than 90^o). This means that \(\ \angle D A B\) and \(\ \angle M L N\) are acute. \(\ \angle T Q S\) is larger than \(\ \angle G F I\), so it is an obtuse angle.

\(\ \angle D A B\) and \(\ \angle M L N\) are acute angles.

\(\ \angle G F I\) is a right angle.

\(\ \angle T Q S\) is an obtuse angle.

Example \(\PageIndex{5}\)

Identify each point, ray, and angle in the figure below.

Solution

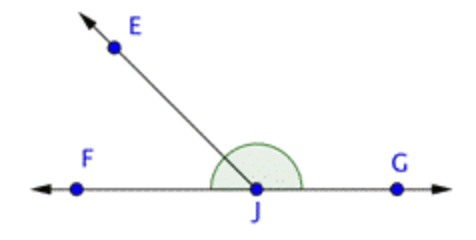	Begin by identifying each point in the figure. There are 4: \(\ E, F, G, \text { and } J\).
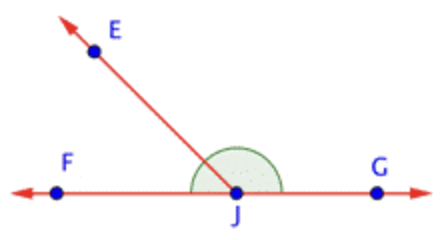	Now find rays. A ray begins at one point, and then continues through another point towards infinity (indicated by an arrow). Three rays start at point \(\ J\): \(\ \overrightarrow{J E}\), \(\ \overrightarrow{J F}\), and \(\ \overrightarrow{J G}\). But also notice that a ray could start at point \(\ F\) and go through \(\ J\) and \(\ G\), and another could start at point \(\ G\) and go through \(\ J\) and \(\ F\). These rays can be represented by \(\ \overrightarrow{G F}\) and \(\ \overrightarrow{F G}\)
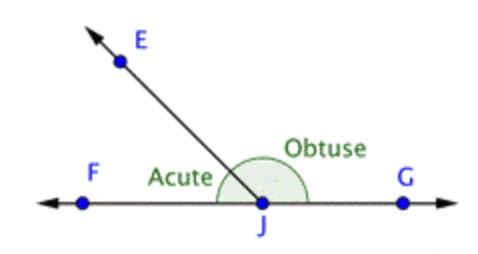	Finally, look for angles. \(\ \angle E J G\) is obtuse, \(\ \angle E J F\) is acute, and \(\ \angle F J G\) is straight. (Don’t forget those straight angles!)
Points: \(\ E, F, G, J\) Rays: \(\ \overrightarrow{J E}, \overrightarrow{J G}, \overrightarrow{J F}, \overrightarrow{G F}, \overrightarrow{F G}\) Angles: \(\ \angle E J G, \angle E J F, \angle F J G\)

Try It \(\PageIndex{2}\)

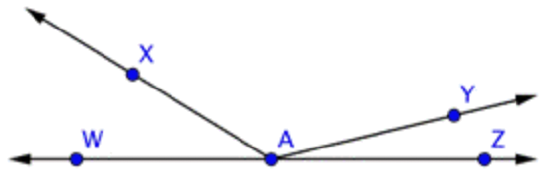
Identify the acute angles in the image below.

Answer

Both \(\ \angle W A X\) and \(\ \angle Y A Z\) are acute angles.

\(\ \angle W A Z\) is a straight angle, and \(\ \angle W A Y\), \(\ \angle X A Y\) and \(\ \angle X A Z\) are obtuse angles.

Measuring Angles with a Protractor

Learning how to measure angles can help you become more comfortable identifying the difference between angle measurements. For instance, how is a 135° angle different from a 45° angle?

Measuring angles requires a protractor, which is a semi-circular tool containing 180 individual hash marks. Each hash mark represents 1°. (Think of it like this: a circle is 360°, so a semi-circle is 180°.) To use the protractor, do the following three steps:

1. line up the vertex of the angle with the dot in the middle of the flat side (bottom) of the protractor,
2. align one side of the angle with the line on the protractor that is at the zero degree mark, and
3. look at the curved section of the protractor to read the measurement.

The example below shows you how to use a protractor to measure the size of an angle.

Example \(\PageIndex{6}\)

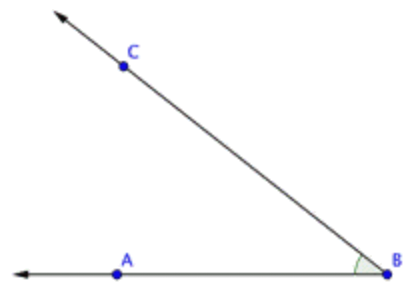
Use a protractor to measure the angle shown below.

Solution

Use a protractor to measure the angle:

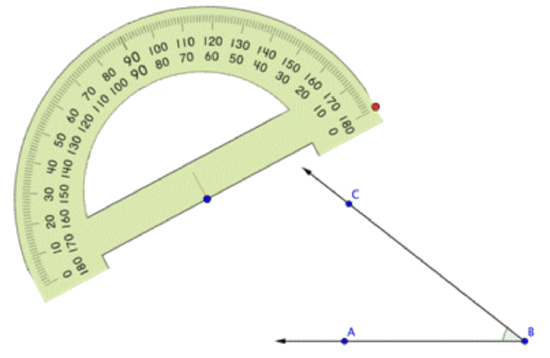
Align the blue dot on the protractor with the vertex of the angle you want to measure:

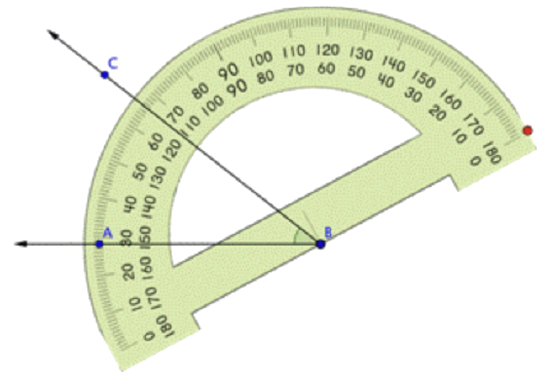
Rotate the protractor around the vertex of the angle until the side of the angle is aligned with the 0 degree mark of the protractor:

Read the measurement, in degrees, of the angle. Begin with the side of the angle that is aligned with the 0° mark of the protractor

and count up from 0^o :

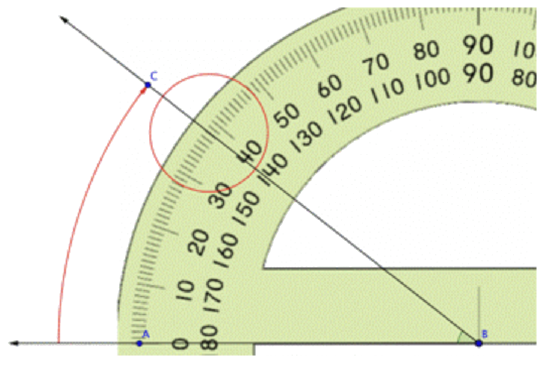
The angle measures 38°.

Try It \(\PageIndex{3}\)

What is the measurement of the angle shown below?

Answer

135°

Summary

Geometric shapes and figures are all around us. A point is a zero-dimensional object that defines a specific location on a plane. A line is made up of an infinite number of points, all arranged next to each other in a straight pattern, and going on forever. A ray begins at one point and goes on towards infinity in one direction only. A plane can be described as a two-dimensional canvas that goes on forever.

When two rays share an endpoint, an angle is formed. Angles can be described as acute, right, obtuse, or straight, and are measured in degrees. You can use a protractor (a special math tool) to closely measure the size of any angle.