2.6: Perimeter and Area
- Page ID
- 113130
- Find the perimeter of a polygon.
- Find the area of a polygon.
- Find the area and perimeter of non-standard polygons.
Introduction
Perimeter and area are two important and fundamental mathematical topics. They help you to quantify physical space and also provide a foundation for more advanced mathematics found in algebra, trigonometry, and calculus. Perimeter is a measurement of the distance around a shape and area gives us an idea of how much surface the shape covers.
Knowledge of area and perimeter is applied practically by people on a daily basis, such as architects, engineers, and graphic designers, and is math that is very much needed by people in general. Understanding how much space you have and learning how to fit shapes together exactly will help you when you paint a room, buy a home, remodel a kitchen, or build a deck.
Perimeter
The perimeter of a two-dimensional shape is the distance around the shape. You can think of wrapping a string around a triangle. The length of this string would be the perimeter of the triangle. Or walking around the outside of a park, you walk the distance of the park’s perimeter. Some people find it useful to think “peRIMeter” because the edge of an object is its rim and peRIMeter has the word “rim” in it.
If the shape is a polygon, then you can add up all the lengths of the sides to find the perimeter. Be careful to make sure that all the lengths are measured in the same units. You measure perimeter in linear units, which is one dimensional. Examples of units of measure for length are inches, centimeters, or feet.
Find the perimeter of the given figure. All measurements indicated are inches.
Solution
| \(\ P=5+3+6+2+3+3\) | Since all the sides are measured in inches, just add the lengths of all six sides to get the perimeter. |
| \(\ P=22 \text { inches }\) | Remember to include units. |
This means that a tightly wrapped string running the entire distance around the polygon would measure 22 inches long.
Find the perimeter of a triangle with sides measuring 6 m, 8 m, and 12 m.
Solution
| \(\ P=6+8+12\) | Since all the sides are measured in meters, just add the lengths of all three sides to get the perimeter. |
Thus, \(\ P=26 \text { m}\).
Sometimes, you need to use what you know about a polygon in order to find the perimeter. Let’s look at the rectangle in the next example.
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the perimeter.
Solution
| \(\ P=3+3+8+8\) | Since this is a rectangle, the opposite sides have the same lengths, 3 cm. and 8 cm. Add up the lengths of all four sides to find the perimeter. |
Thus, \(\ P=22 \text { centimeters}\).
Notice that the perimeter of a rectangle always has two pairs of equal length sides. In the above example you could have also written \(\ P=2(3)+2(8)=6+16=22 \mathrm{~cm}\). The formula for the perimeter of a rectangle is often written as \(\ P=2 l+2 w\), where \(\ l\) is the length of the rectangle and \(\ w\) is the width of the rectangle.
Area of Parallelograms
The area of a two-dimensional figure describes the amount of surface the shape covers. You measure area in square units of a fixed size. Examples of square units of measure are square inches, square centimeters, or square miles. When finding the area of a polygon, you count how many squares of a certain size will cover the region inside the polygon.
Let’s look at a 4 by 4 square.
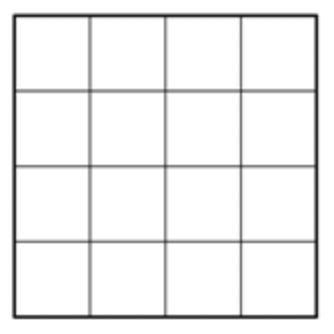
You can count that there are 16 squares, so the area is 16 square units. Counting out 16 squares doesn’t take too long, but what about finding the area if this is a larger square or the units are smaller? It could take a long time to count.
Fortunately, you can use multiplication. Since there are 4 rows of 4 squares, you can multiply \(\ 4 \cdot 4\) to get 16 squares! And this can be generalized to a formula for finding the area of a square with any length, \(\ s\): \(\ \text { Area }=s \cdot s=s^{2}\).
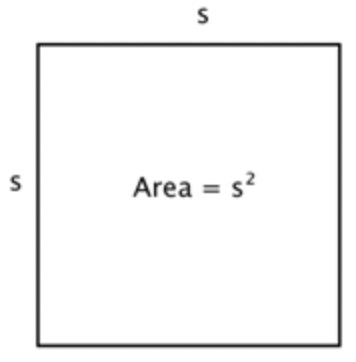
You can write “\(\ \mathrm{in}^{2}\)” for square inches and “\(\ \mathrm{ft}^{2}\)” for square feet.
To help you find the area of the many different categories of polygons, mathematicians have developed formulas. These formulas help you find the measurement more quickly than by simply counting. The formulas you are going to look at are all developed from the understanding that you are counting the number of square units inside the polygon. Let’s look at a rectangle.
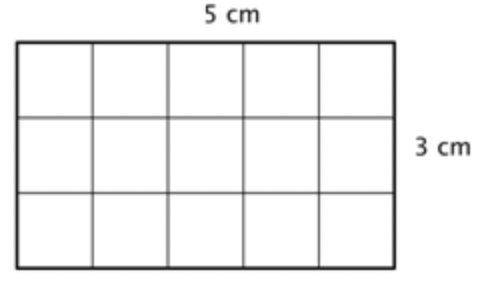
You can count the squares individually, but it is much easier to multiply 3 times 5 to find the number more quickly. And, more generally, the area of any rectangle can be found by multiplying length times width.
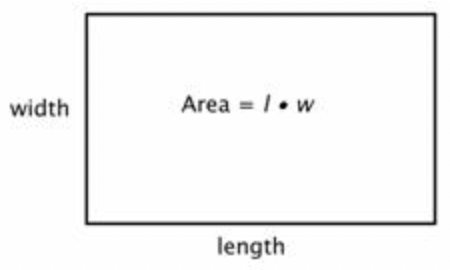
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the area.
Solution
| \(\ A=l \cdot w\) | Start with the formula for the area of a rectangle, which multiplies the length times the width. |
| \(\ A=8 \cdot 3\) | Substitute 8 for the length and 3 for the width. |
| \(\ A=24 \mathrm{~cm}^{2}\) | Be sure to include the units, in this case square centimeters. |
It would take 24 squares, each measuring 1 centimeter on a side, to cover this rectangle.
The formula for the area of any parallelogram (remember, a rectangle is a type of parallelogram) is the same as that of a rectangle: \(\ \text { Area }=l \cdot w\). Notice in a rectangle, the length and the width are perpendicular. This should also be true for all parallelograms. Base (\(\ b\) for the length (of the base), and height (\(\ h\)) for the width of the line perpendicular to the base is often used. So the formula for a parallelogram is generally written, \(\ A=b \cdot h\).
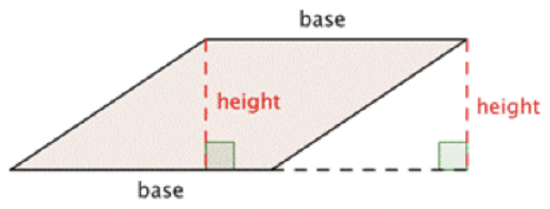
Find the area of the parallelogram.
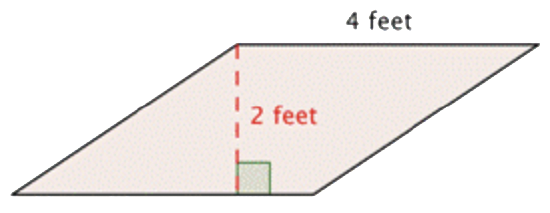
Solution
| \(\ A=b \cdot h\) | Start with the formula for the area of a parallelogram: |
| \(\ A=4 \cdot 2\) |
\(\ \text { Area }=\text { base } \cdot \text { height }\). Substitute the values into the formula. |
| \(\ A=8\) | Multiply. |
The area of the parallelogram is 8 \(\ \mathrm{ft}^{2}\).
Find the area of a parallelogram with a height of 12 feet and a base of 9 feet.
- Answer
-
The height of the parallelogram is 12 and the base of the parallelogram is 9; the area is 12 times 9, or \(\ 108 \text{ ft}^{2}\).
Area of Triangles and Trapezoids
The formula for the area of a triangle can be explained by looking at a right triangle. In the image below is a rectangle with the same height and base as the original triangle. The area of the triangle is one half of the rectangle!
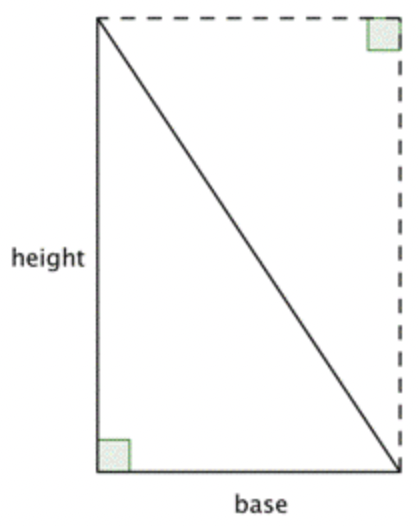
Since the area of two congruent triangles is the same as the area of a rectangle, you can come up with the formula \(\ \text { Area }=\dfrac{1}{2} b \cdot h\) to find the area of a triangle.
When you use the formula for a triangle to find its area, it is important to identify a base and its corresponding height, which is perpendicular to the base.
A triangle has a height of 4 inches and a base of 10 inches. Find the area.
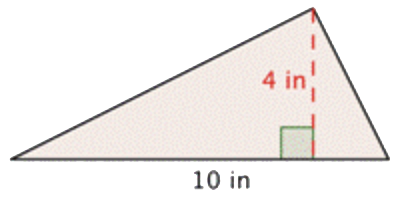
Solution
| \(\ A=\dfrac{1}{2} b h\) | Start with the formula for the area of a triangle. |
| \(\ A=\dfrac{1}{2} \cdot 10 \cdot 4\) | Substitute 10 for the base and 4 for the height. |
| \(\begin{array}{c} A=\dfrac{1}{2} \cdot 40\\ A=20 \end{array}\) |
Multiply. |
Thus, the area is \(\ A=20 \text { in}^{2}\).
Now let’s look at the trapezoid. To find the area of a trapezoid, take the average length of the two parallel bases and multiply that length by the height: \(\ A=\dfrac{1}{2} \left(b_{1}+b_{2}\right) h\).
An example is provided below. Notice that the height of a trapezoid will always be perpendicular to the bases (just like when you find the height of a parallelogram).
Find the area of the trapezoid.
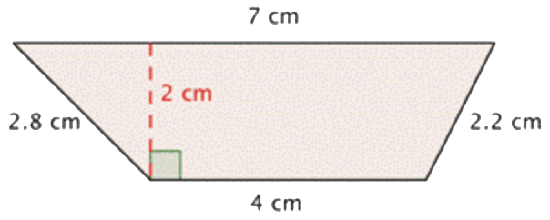
Solution
| \(\ A=\dfrac{\left(b_{1}+b_{2}\right)}{2} h\) | Start with the formula for the area of a trapezoid. |
| \(\ \begin{array}{c} A=\dfrac{(4+7)}{2} \cdot 2 \\ A=\dfrac{11}{2} \cdot 2 \\ A=11 \end{array}\) |
Substitute 4 and 7 for the bases and 2 for the height, and find \(\ A\). |
The area of the trapezoid is \(\ 11 \mathrm{~cm}^{2}\).
Use the following formulas to find the areas of different shapes.
square: \(\ A=s^{2}\)
rectangle: \(\ A=l \cdot w\)
parallelogram: \(\ A=b \cdot h\)
triangle: \(\ A=\dfrac{1}{2} b \cdot h\)
trapezoid: \(\ A=\dfrac{\left(b_{1}+b_{2}\right)}{2} h\)
Working with Perimeter and Area
Often you need to find the area or perimeter of a shape that is not a standard polygon. Artists and architects, for example, usually deal with complex shapes. However, even complex shapes can be thought of as being composed of smaller, less complicated shapes, like rectangles, trapezoids, and triangles.
To find the perimeter of non-standard shapes, you still find the distance around the shape by adding together the length of each side.
Finding the area of non-standard shapes is a bit different. You need to create regions within the shape for which you can find the area, and add these areas together. Have a look at how this is done below.
Find the area and perimeter of the polygon.
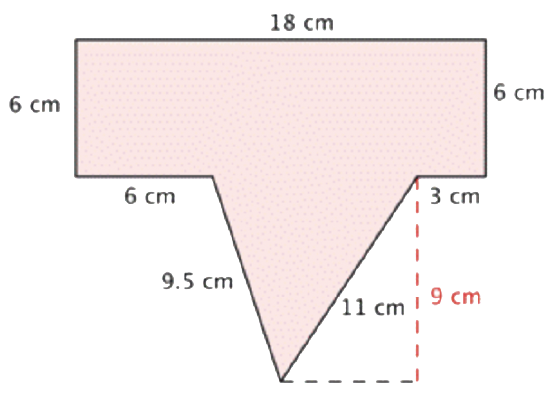
Solution
| \(\ \begin{array}{r} P=18+6+3+11+9.5+6+6 \\ P=59.5 \mathrm{~cm} \end{array}\) |
To find the perimeter, add together the lengths of the sides. To stay organized, start at the top and work clockwise around the shape. |
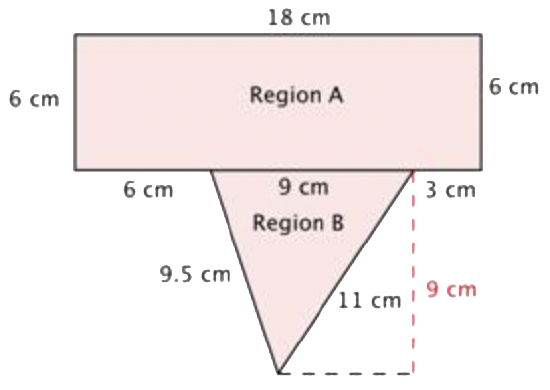 Area of Polygon = (Area of A) + (Area of B) |
To find the area, divide the polygon into two separate, simpler regions. The area of the entire polygon will equal the sum of the areas of the two regions. |
| \(\ \begin{array}{r} \text { Area of Region } A=l \cdot w\\ =18\cdot 6\\=108 \end{array}\) |
Region A is a rectangle. To find the area, multiply the length (18) by the width (6). The area of Region A is 108 cm2. |
| \(\ \begin{array}{r} \text{Area of Region } \mathrm{B}=\dfrac{1}{2} b \cdot h \\ =\dfrac{1}{2} \cdot 9 \cdot 9 \\ =\dfrac{1}{2} \cdot 81 \\ =40.5 \end{array}\) |
Region B is a triangle. To find the area, use the formula \(\ \dfrac{1}{2} b h\), where the base is 9 and the height is 9. The area of Region B is 40.5 cm2. |
| \(\ 108 \mathrm{~cm}^{2}+40.5 \mathrm{~cm}^{2}=148.5 \mathrm{~cm}^{2}\) | Add the regions together. |
\(\ \begin{array}{c}
\text { Perimeter }=59.5 \mathrm{~cm} \\
\text { Area }=148.5 \mathrm{~cm}^{2}
\end{array}\)
You also can use what you know about perimeter and area to help solve problems about situations like buying fencing or paint, or determining how big a rug is needed in the living room. Here’s a fencing example.
Rosie is planting a garden with the dimensions shown below. She wants to put a thin, even layer of mulch over the entire surface of the garden. The mulch costs $3 per square foot. How much money will she have to spend on mulch?
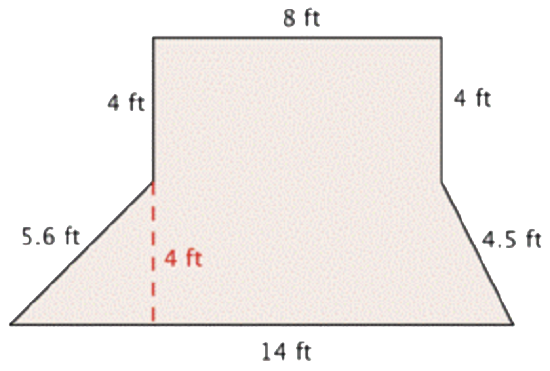
Solution
 |
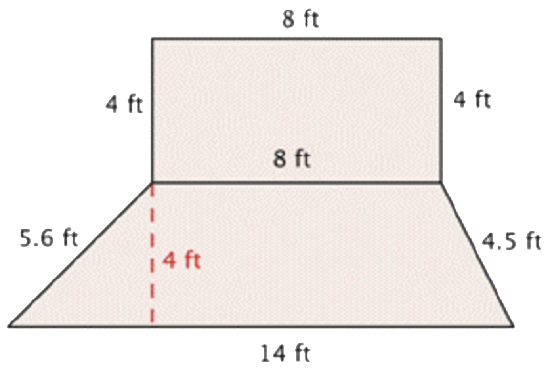This shape is a combination of two simpler shapes: a rectangle and a trapezoid. Find the area of each. |
| \(\ \begin{array}{r} A=l \cdot w \\ A=8 \cdot 4 \\ A=32 \text{ ft}^{2} \end{array}\) |
Find the area of the rectangle. |
| \(\ \begin{array}{r} A=\dfrac{\left(b_{1}+b_{2}\right)}{2} h \\ A=\dfrac{(14+8)}{2} \cdot 4 \\ A=\dfrac{22}{2} \cdot 4 \\ A=11 \cdot 4 \\ A=44 \text{ ft}^{2} \end{array}\) |
Find the area of the trapezoid. |
| \(\ 32 \text{ ft}^{2}+44 \text{ ft}^{2}=76 \text{ ft}^{2}\) | Add the measurements. |
| \(\ 76 \text{ ft}^{2} \cdot \$ 3=\$ 228\) | Multiply by $3 to find out how much Rosie will have to spend. |
Rosie will spend $228 to cover her garden with mulch.
Find the area of the shape shown below.
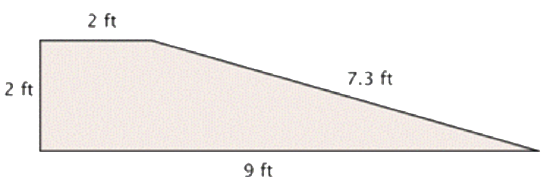
- Answer
-
This shape is a trapezoid, so you can use the formula \(\ A=\dfrac{\left(b_{1}+b_{2}\right)}{2} h\) to find the area: \(\ A=\dfrac{(2+9)}{2} \cdot 2 = 11 \text{ ft}^2\).
Summary
The perimeter of a two-dimensional shape is the distance around the shape. For a polygon this is found by adding up all the sides (as long as they are all the same unit). The area of a two-dimensional shape is found by counting the number of squares that cover the shape. Many formulas have been developed to quickly find the area of standard polygons, like triangles and parallelograms.