2.10: Right Triangle Trigonometry
- Page ID
- 121738
- Use the Pythagorean Theorem to find the missing lengths of the sides of a right triangle.
- Find the missing lengths and angles of a right triangle.
- Solve applied problems using right-triangle trigonometry.
Introduction
Suppose you have to build a ramp and don’t know how long it needs to be. You know certain angle measurements and side lengths, but you need to find the missing pieces of information.
There are six trigonometric functions, or ratios, that you can use to compute what you don’t know. You will now learn how to use these six functions to solve right-triangle application problems.
Using the Pythagorean Theorem in Trigonometry Problems
There are several ways to determine the missing information in a right triangle. One of these ways is the Pythagorean Theorem, which states that \(a^2 + b^2 = c^2\).
Suppose you have a right triangle in which a and b are the lengths of the legs, and c is the length of the hypotenuse, as shown below.
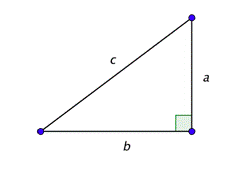
If you know the length of any two sides, then you can use the Pythagorean Theorem (\(a^2 + b^2 = c^2\)) to find the length of the third side. Once you know all the side lengths, you can compute all of the trigonometric functions.
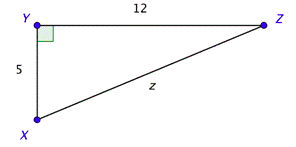
Problem: Find the values of side \(z\).
Answer
Use the Pythagorean Theorem to find the length of the hypotenuse.
\(\begin{array}{c}
5^{2}+12^{2}=z^{2} \\
25+144=z^{2} \\
169=z^{2} \\
13=z
\end{array}\)
Solving Right Triangles
Determining all of the side lengths and angle measures of a right triangle is known as solving a right triangle. Let’s look at how to do this when you’re given one side length and one acute angle measure. Once you learn how to solve a right triangle, you’ll be able to solve many real world applications, such as the ramp problem at the beginning of this lesson, and the only tools you’ll need are the definitions of the trigonometric functions, the Pythagorean Theorem, and a calculator.
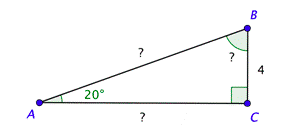
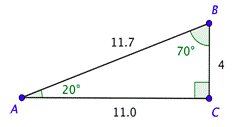
Problem: You need to build a ramp with the following dimensions. Solve the right triangle shown below. Use the approximations \(\sin 20^{\circ} \approx 0.342\) and \(\tan 20^{\circ} \approx 0.364\), and give the lengths to the nearest tenth.
Answer
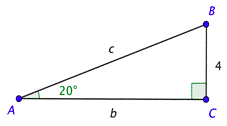
Remember that the acute angles in a right triangle are complementary, which means their sum is \(90^{\circ}\). Since \(m \angle A=20^{\circ}\), it follows that \(m \angle B=90^{\circ}-20^{\circ}=70^{\circ}\).
You can use the definition of sine to find \(c\). Substitute the measure of the angle on the left side of the equation and use the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(c \approx 11.7\).
\(\begin{array}{c}
\sin 20^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }} \\
0.342 \approx \frac{4}{c} \\
c(0.342) \approx 4 \\
c \approx \frac{4}{0.342} \approx 11.695
\end{array}\)
In a similar way, you can use the definition of tangent and the measure of the angle to find \(b\). Solving the equation and rounding to the nearest tenth gives you \(b \approx 11.0\).
\(\begin{array}{c}
\tan 20^{\circ}=\frac{\text { opposite }}{\text { adjacent }} \\
0.364 \approx \frac{4}{b} \\
0.364 b \approx 4 \\
b \approx \frac{4}{0.364} \approx 10.989
\end{array}\)
The ramp needs to be 11.7 feet long.
In the problem above, you were given the values of the trigonometric functions. In the next problem, you’ll need to use the trigonometric function keys on your calculator to find those values.
Problem: Solve the right triangle shown below. Give the lengths to the nearest tenth.
Answer
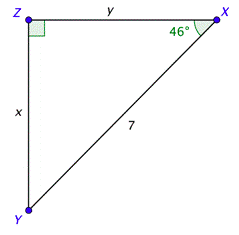
The acute angles are complementary, which means their sum is \(90^{\circ}\). Since \(\text { Since } m \angle X=46^{\circ}\), it follows that \(m \angle Y=90^{\circ}-46^{\circ}=44^{\circ}\).
You can use the definition of sine to find \(x\). Use your calculator to find the value of \(\sin 46^{\circ}\) and the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(x \approx 5.0\).
\(\begin{array}{c}
\sin 46^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }} \\
0.72 \approx \frac{x}{7} \\
7(0.72) \approx x \\
5.04 \approx x
\end{array}\)
To find \(y\), you can either use another trigonometric function (such as cosine) or you can use the Pythagorean Theorem. Solving the equation and rounding to the nearest tenth gives you \(y \approx 4.9\).
\(\begin{array}{c}
5.0^{2}+y^{2} \approx 7^{2} \\
25+y^{2} \approx 49 \\
y^{2} \approx 24 \\
y \approx \sqrt{24} \\
y \approx 4.899
\end{array}\)
We now know all three sides and all three angles. Their values are shown in the drawing.
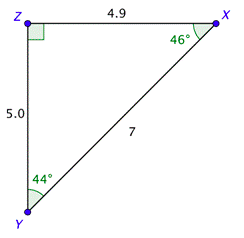
Sometimes you may be given enough information about a right triangle to solve the triangle, but that information may not include the measures of the acute angles. In this situation, you will need to use the inverse trigonometric function keys on your calculator to solve the triangle.
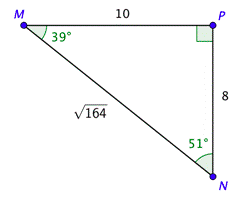
Problem: Solve the right triangle shown below, given that \(\tan N =\frac{5}{4}\). Find the exact side lengths and approximate the angles to the nearest degree.
Answer
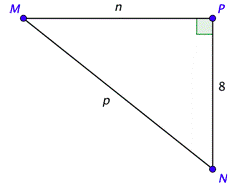
You are not given an angle measure, but you can use the definition of tangent to find the value of \(n\).
Use the ratio you are given on the left side and the information from the triangle on the right side. Cross-multiply and solve for \(n\).
\(\begin{aligned}
\tan N &=\frac{\text { opposite }}{\text { adjacent }} \\
\frac{5}{4} &=\frac{n}{8} \\
40 &= 4 n \\
n &=10
\end{aligned}\)
Use the Pythagorean Theorem to find the value of \(p\).
\(\begin{array}{c}
10^{2}+8^{2}=p^{2} \\
100+64=p^{2} \\
164=p^{2} \\
\sqrt{164}=p
\end{array}\)
We can use the triangle to find a value of the tangent and the inverse tangent key on your calculator to find the angle that yields that value. Rounding to the nearest degree, \(\angle M\) is approximately \(39^{\circ}\), \(M \approx 39^{\circ}\). Subtract \(39^{\circ}\), from \(90^{\circ}\) to get \(N \approx 51^{\circ}\).
\(\begin{array}{c}
\tan M=\frac{8}{10}=0.8 \\
M=\tan ^{-1} 0.8 \\
M \approx 38.7^{\circ}
\end{array}\)
We now know all three sides and all three angles. Their values are shown in the drawing.
What is the value of \(x\) to the nearest hundredth?
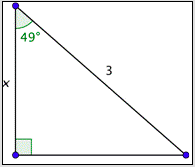
- 4.57
- 1.97
- 0.90
- 0.22
- Answer
-
- 4.57. Incorrect. You probably set up the ratio incorrectly, equating \(\cos 49^{\circ}\) and \(\frac{3}{x}\). A correct way to set up the equation is \(\cos 49^{\circ}=\frac{x}{3}\). The correct answer is 1.97.
- 1.97. Correct. One way to set up a correct equation is to use the definition of cosine. This will give you \(\cos 49^{\circ}=\frac{x}{3}\). The solution to this equation is: \(x=3 \cdot \cos 49^{\circ} \approx 3 \cdot(0.656)=1.968\). This rounds to 1.97.
- 0.90. Incorrect. You probably set up the correct equation, \(\cos 49^{\circ}=\frac{x}{3}\), and solved it correctly. However, your calculator was not set to degrees. The correct answer is 1.97.
- 0.22. Incorrect. You may have correctly set up your equation as \(\cos 49^{\circ}=\frac{x}{3}\), but then incorrectly solved it as \(x=\frac{\cos 49^{\circ}}{3}\). The correct answer is 1.97.
Using Trigonometry in Real-World Problems
There are situations in the real world, such as building a ramp for a loading dock, in which you have a right triangle with certain information about the sides and angles, and you wish to find unknown measures of sides or angles. This is where understanding trigonometry can help you.
Problem: Ben and Emma are out flying a kite. Emma can see that the kite string she is holding is making a \(70^{\circ}\) angle with the ground. The kite is directly above Ben, who is standing 50 feet away. To the nearest foot, how many feet of string has Emma let out?
Answer
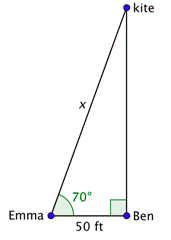
We want to find the length of string let out. It is the hypotenuse of the right triangle shown.
Since the 50-foot distance measures the adjacent side to the \(70^{\circ}\) angle, you can use the cosine function to find \(x\).
\(\cos 70^{\circ}=\frac{50}{x}\)
Solve the equation for \(x\). Use a calculator to find a numerical value. The answer rounds to 146.
\(\begin{array}{c}
x \cdot \cos 70^{\circ}=50 \\
x=\frac{50}{\cos 70^{\circ}} \\
x=\frac{50}{0.342 \ldots} \\
x=146.19 \ldots
\end{array}\)
Emma has let out approximately 146 feet of string.
In the example above, you were given one side and an acute angle. In the next one, you’re given two sides and asked to find an angle. Finding an angle will usually involve using an inverse trigonometric function. The Greek letter theta, \(\theta\), is commonly used to represent an unknown angle. In this example, \(\theta\) represents the angle of elevation.
Problem: A wheelchair ramp is placed over a set of stairs so that one end is 2 feet off the ground. The other end is at a point that is a horizontal distance of 28 feet away, as shown in the diagram. What is the angle of elevation to the nearest tenth of a degree?
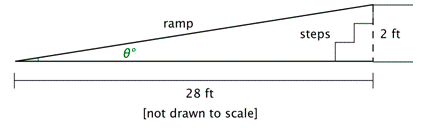
Answer
The angle of elevation is labeled \(\theta ^{\circ}\) in the diagram. The lengths given are the sides opposite and adjacent to this angle, so you can use the tangent function to find \(\theta\).
You want to find the measure of an angle that gives you a certain tangent value. This means that you need to find the inverse tangent. Remember that you have to use the keys 2ND and TAN on your calculator. Look at the hundredths place to round to the nearest tenth.
\(\begin{aligned}
\tan \theta^{\circ} &=\frac{2}{28} \\
\tan \theta^{\circ} &=\frac{1}{14} \\
\theta^{\circ} &=\tan ^{-1}\left(\frac{1}{14}\right) \\
\theta &=4.0856 \ldots
\end{aligned}\)
The angle of elevation is approximately \(4.1^{\circ}\).
Sometimes the right triangle can be part of a bigger picture.
A guy wire is attached to a telephone pole 3 feet below the top of the pole, as shown below. The guy wire is anchored 14 feet from the telephone pole and makes a \(64^{\circ}\) angle with the ground. How high up the pole is the guy wire attached? Round your answer to the nearest tenth of a foot.
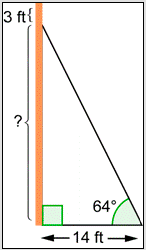
- \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\)
- \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\)
- \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\)
- \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\)
- Answer
-
- \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\). Incorrect. You may have been confused as to which ratio corresponds to which trigonometric function. You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
- \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\). Correct. Let \(x\) represent the vertical distance from the base of the telephone pole up to where the guy wire is attached. Then \(\tan 64^{\circ}=\frac{x}{14}\). Solving this equation for \(x\) gives you \(x=14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
- \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\). Incorrect. It looks like you set up and solved the correct equation to find the unknown length. However, you misread the problem. When you added the 3 you found the height of the entire pole. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
- \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\). Incorrect. It looks like you set up and solved an equation to find the length of the wire (the hypotenuse of the triangle). You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
Summary
There are many ways to find the missing side lengths or angle measures in a right triangle. Solving a right triangle can be accomplished by using the definitions of the trigonometric functions and the Pythagorean Theorem. This process is called solving a right triangle. Being able to solve a right triangle is useful in solving a variety of real-world problems such as the construction of a wheelchair ramp.


