5.9: Trigonometry Preview - Circles
- Page ID
- 91186
Recall from Geometry that a circle can be determined by fixing a point (called the center) and a positive number (called the radius) as follows.
A circle with center \((h,k)\) and radius \(r>0\) is the set of all points \((x, y)\) in the plane whose distance to \((h,k)\) is \(r\).
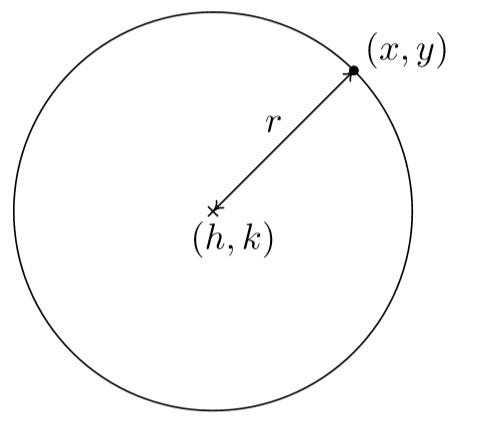
From the picture, we see that a point \((x,y)\) is on the circle if and only if its distance to \((h,k)\) is \(r\). We express this relationship algebraically using the Distance Formula, as
\[r = \sqrt{(x - h)^2 + (y-k)^2} \nonumber\]
By squaring both sides of this equation, we get an equivalent equation (since \(r > 0\)) which gives us the standard equation of a circle.
The standard form of the equation of a circle with center \((h,k)\) and radius \(r >0\) is
\[(x-h)^2 + (y-k)^2 = r^2. \nonumber\]
Write the standard equation of the circle with center (−2,3) and radius 5.
Solution.
Here, \((h,k) = (-2,3)\) and \(r = 5\), so we get
\[\begin{array}{rcl} (x-(-2))^2+(y-3)^2 &= &(5)^2 \\ (x+2)^2+(y-3)^2 & = & 25 \end{array} \nonumber\]
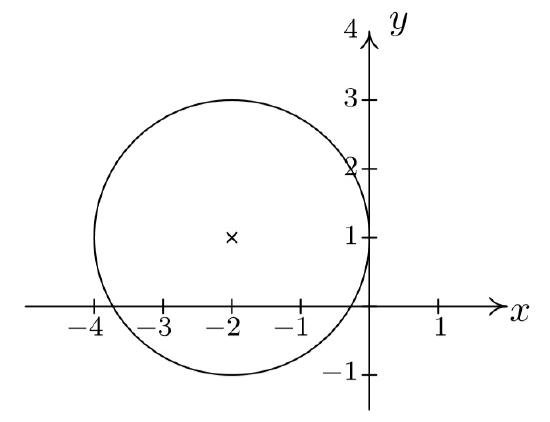
Graph \((x+2)^2+(y-1)^2 = 4\). Find the center and radius.
Solution
From the standard form of a circle, we have that \(x + 2\) is \(x-h\), so \(h = -2\) and \(y - 1\) is \(y - k\) so \(k = 1\). This tells us that our center is \((-2,1)\). Furthermore, \(r^2 = 4\), so \(r = 2\). Thus we have a circle centered at \((-2,1)\) with a radius of \(2\). Graphing gives us
If we were to expand the equation in the previous example and gather up like terms, instead of the easily recognizable \((x+2)^2 + (y-1)^2 = 4\), we'd be contending with \(x^2 + 4x + y^2 - 2y + 1 = 0.\) If we're given such an equation, we can complete the square to rewrite the equation in standard form for a circle.
Complete the square to find the center and radius of \(3x^2 - 6x + 3y^2 + 4y -4 = 0\).
Solution
\[ \begin{array}{rclr} 3x^2 - 6x + 3y^2 + 4y -4 & = & 0 & \\ 3x^2 - 6x + 3y^2 + 4y & = & 4 & \mbox{add \(4\) to both sides} \\ 3\left(x^2 - 2x \right) + 3\left(y^2 + \dfrac{4}{3} y\right) & = & 4 & \mbox{factor out leading coefficients} \\ 3\left(x^2 - 2x + \underline{1} \right) + 3\left(y^2 + \dfrac{4}{3} y + \underline{\underline{\dfrac{4}{9}}} \right) & = & 4 + 3\underline{(1)} + 3\underline{\underline{\left(\dfrac{4}{9}\right)}} & \mbox{complete the square in \(x\), \(y\)} \\ 3(x - 1)^2 + 3\left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{3} & \mbox{factor} \\ (x - 1)^2 + \left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{9} & \mbox{divide both sides by \(3\)}\end{array} \nonumber\]
From the standard form of a circle, we identify \(x - 1\) as \(x - h\), so \(h = 1\), and \(y + \frac{2}{3}\) as \(y - k\), so \(k = - \frac{2}{3}\). Hence, the center is \((h,k) = \left(1, -\frac{2}{3}\right)\). Furthermore, we see that \(r^2 = \frac{25}{9}\) so the radius is \(r = \frac{5}{3}\).
It is possible to obtain equations like \((x-3)^2 + (y+1)^2 = 0\) or \((x-3)^2 + (y+1)^2 = -1\), neither of which describes a circle. (Do you see why not?) The reader is encouraged to think about what, if any, points lie on the graphs of these two equations.
Write the standard equation of the circle which has \((-1,3)\) and \((2,4)\) as the endpoints of a diameter.
Solution
We recall that a diameter of a circle is a line segment containing the center and two points on the circle. Plotting the given data yields
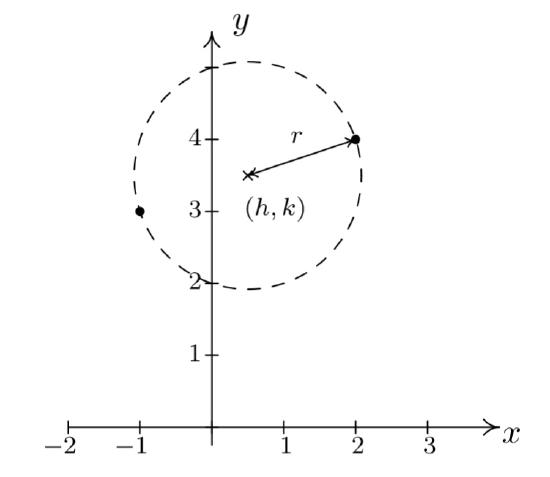
Since the given points are endpoints of a diameter, we know their midpoint \((h, k)\) is the center of the circle. Equation \ref{midpointformula} gives us
\[ \begin{array}{rcl} (h,k) & = & \left( \dfrac{x_{\mbox{1}} + x_{\mbox{2}}}{2}, \dfrac{y_{\mbox{1}} + y_{\mbox{2}}}{2} \right) \\ & = & \left( \dfrac{-1+2}{2}, \dfrac{3+4}{2} \right) \\ & = & \left( \dfrac{1}{2}, \dfrac{7}{2} \right) \end{array} \nonumber\]
The diameter of the circle is the distance between the given points, so we know that half of the distance is the radius. Thus,
\[ \begin{array}{rcl} r & = & \dfrac{1}{2} \sqrt{\left(x_{\mbox{2}} - x_{\mbox{1}}\right)^2+\left(y_{\mbox{2}}-y_{\mbox{1}}\right)^2} \\ & = & \dfrac{1}{2} \sqrt{(2-(-1))^2+(4-3)^2} \\ & = & \dfrac{1}{2} \sqrt{3^2+1^2} \\ & = &\dfrac{\sqrt{10}}{2} \end{array} \nonumber\]
Finally, since \(\left( \dfrac{\sqrt{10}}{2} \right)^2 = \dfrac{10}{4}\), our answer becomes \(\left(x - \dfrac{1}{2} \right)^2 + \left(y - \dfrac{7}{2} \right)^2 =\dfrac{10}{4}\)
We close this section with a very important circle that you will learn more about in trigonometry: the Unit Circle.
The Unit Circle is the circle centered at \((0,0)\) with a radius of \(1\). The standard equation of the Unit Circle is \(x^2 + y^2 = 1.\)
Find the points on the unit circle with \(y\)-coordinate \(\dfrac{\sqrt{3}}{2}\).
Solution
We replace \(y\) with \(\dfrac{\sqrt{3}}{2}\) in the equation \(x^2 + y^2 = 1\) to get
\[ \begin{array}{rcl} x^2 + y^2 & = & 1 \\ x^2 + \left(\dfrac{\sqrt{3}}{2}\right)^2 & = & 1 \\ \dfrac{3}{4} + x^2 & = & 1 \\ x^2 & = & \dfrac{1}{4} \\ x & = & \pm \sqrt{\dfrac{1}{4}} \\ x & = & \pm \dfrac{1}{2} \end{array} \nonumber\]
Our final answers are \(\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)\) and \(\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)\).


