2.1: Adding Integers
- Page ID
- 57431
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Like our work with the whole numbers, addition of integers is best explained through the use of number line diagrams. However, before we start, let’s take a moment to discuss the concept of a vector.
Vectors
A vector is a mathematical object that possesses two import qualities: (1) magnitude or length, and (2) direction.
Vectors are a fundamental problem solving tool in mathematics, science, and engineering. In physics, vectors are used to represent forces, position, velocity, and acceleration, while engineers use vectors to represent both internal and external forces on structures, such as bridges and buildings. In this course, and in this particular section, we will concentrate on the use of vectors to help explain addition of integers.
Vectors on the Number Line
Consider the number line in Figure \(\PageIndex{1}\).
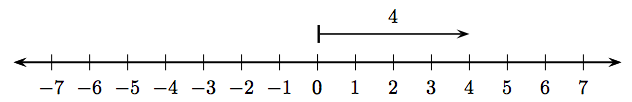
Above the line we’ve drawn a vector with tail starting at the integer 0 and arrowhead finishing at the integer 4. There are two important things to note about this vector:
- The magnitude (length) of the vector in Figure \(\PageIndex{1}\) is four.
- The vector in Figure \(\PageIndex{1}\) points to the right.
We will agree that the vector in Figure \(\PageIndex{1}\) represents positive four. It is not important that the vector start at the origin. Consider, for example, the vector pictured in Figure \(\PageIndex{2}\).

Again, there are two important observations to be made:
- The magnitude (length) of the vector in Figure \(\PageIndex{2}\) is four.
- The vector in Figure \(\PageIndex{2}\) points to the right.
Hopefully, you have the idea. Any vector that has length 4 and points to the right will represent positive four, regardless of its starting or finishing point. Conversely, consider the vector in Figure \(\PageIndex{3}\), which starts at the integer 4 and finishes at the integer −3.
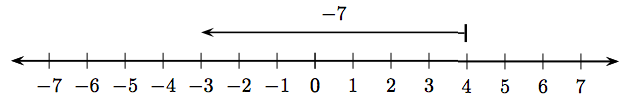
Two observations:
- The magnitude (length) of the vector in Figure \(\PageIndex{3}\) is seven.
- The vector in Figure \(\PageIndex{3}\) points to the left.
We will agree that the vector in Figure \(\PageIndex{3}\) represents negative seven. We could select different starting and finishing points for our vector, but as long as the vector has length seven and points to the left, it represents the integer −7.
Important Observation
A vector pointing to the right represents a positive number. A vector pointing to the left represents a negative number.
Magnitude and Absolute Value
In Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\), the vectors pictured represent the integer positive four. Note that the absolute value of four is four; that is, |4| = 4. Note also that this absolute value is the magnitude or length of the vectors representing the integer positive four in Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\).
In Figure \(\PageIndex{3}\), the vector pictured represents the integer −7. Note that | − 7| = 7. This shows that the absolute value represents the magnitude or length of the vector representing −7.
Magnitude and Absolute Value
If a is an integer, then |a| gives the magnitude or length of the vector that represents the integer a.
Adding Integers with Like Signs
Because the positive integers are also whole numbers, we’ve already seen how to add to them in Section 1.2.
Example 1
Find the sum 3 + 4.
Solution
To add the positive integers 3 and 4, proceed as follows.
- Start at the integer 0, then draw a vector 3 units in length pointing to the right, as shown in Figure \(\PageIndex{4}\). This arrow has magnitude (length) three and represents the positive integer 3.
- Draw a second vector of length four that points to the right, starting at the end of the first vector representing the positive integer 3. This arrow has magnitude (length) four and represents the positive integer 4.
- The sum of the positive integers 3 and 4 could be represented by a vector that starts at the integer 0 and ends at the positive integer 7. However, we prefer to mark this sum on the number line as a solid dot at the positive integer 7. This integer represents the sum of the positive integers 3 and 4.
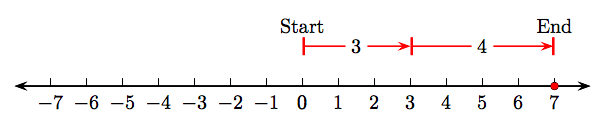
Thus, 3 + 4 = 7
Exercise
Use a number line diagram to show the sum 5 + 7.
- Answer
-
12
Negative integers are added in a similar fashion.
Example 2
Find the sum −3+(−4).
Solution
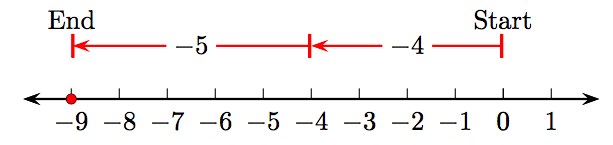
To add the negative integers −3 and −4, proceed as follows.
- Start at the integer 0, then draw a vector 3 units in length pointing to the left, as shown in Figure \(\PageIndex{5}\). This arrow has magnitude (length) three and represents the negative integer −3.
- Draw a second vector of length four that points to the left, starting at the end of the first vector representing the negative integer −3. This arrow has magnitude (length) four and represents the negative integer −4.
- The sum of the negative integers −3 and −4 could be represented by a vector that starts at the integer 0 and ends at the negative integer −7. However, we prefer to mark this sum on the number line as a solid dot at the negative integer −7. This integer represents the sum of the negative integers −3 and −4.

Thus, −3+(−4) = −7.
Drawing on Physical Intuition. Imagine that you are “walking the number line” in Figure \(\PageIndex{5}\). You start at the origin (zero) and take 3 paces to the left. Next, you walk an additional four paces to the left, landing at the number −7
Exercise
Use a number line diagram to show the sum −7+(−3).
- Answer
-
−10
It should come as no surprise that the procedure used to add two negative integers comprises two steps.
Adding Two Negative Integers
To add two negative integers, proceed as follows:
- Add the magnitudes of the integers.
- Prefix the common negative sign
Example 3
Find the sums: (a) −4+(−5), (b) −12 + (−9), and (c) −2+(−16).
Solution
We’ll examine three separate but equivalent approaches, as discussed in the narrative above.
a) The number line schematic
shows that (−4) + (−5) = −9.
b) Drawing on physical intuition, start at zero, walk 12 units to the left, then an additional 9 units to the left. You should find yourself 21 units to the left of the origin (zero). Hence, −12 + (−9) = −21.
c) Following the algorithm above in “Adding Two Negative Integers,” first add the magnitudes of −2 and −16; that is, 2+16 = 18. Now prefix the common sign. Hence, −2+(−16) = −18.
Exercise
Find the sum: −5+(−9).
- Answer
-
−14
Adding Integers with Unlike Signs
Adding integers with unlike signs is no harder than adding integers with like signs.
Example 4
Find the sum −8 + 4.
Solution
To find the sum −8 + 4, proceed as follows:
- Start at the integer 0, then draw a vector eight units in length pointing to the left, as shown in Figure \(\PageIndex{6}\). This arrow has magnitude (length) eight and represents the negative integer −8.
- Draw a second vector of length four that points to the right, starting at the end of the first vector representing the negative integer −8. This arrow (also shown in Figure \(\PageIndex{6}\)) has magnitude (length) four and represents the positive integer 4.
- The sum of the negative integers −8 and 4 could be represented by a vector that starts at the integer 0 and ends at the negative integer −4. However, we prefer to mark this sum on the number line as a solid dot at the negative integer −4. This integer represents the sum of the integers −8 and 4.
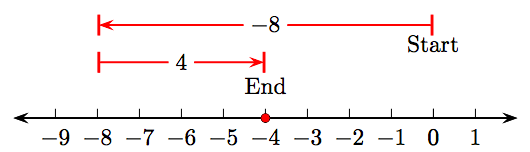
Thus, −8+4= −4.
Drawing on Physical Intuition. Imagine you are “walking the number line in Figure \(\PageIndex{6}\). You start at the origin (zero) and walk eight paces to the left. Next, turn around and walk four paces to the right, landing on the number −4.
Exercise
Use a number line diagram to show the sum −9 + 2.
- Answer
-
−7
Note that adding integers with unlike signs is a subtractive process. This is due to the reversal of direction experienced in drawing Figure \(\PageIndex{6}\) in Example 4.
Adding Two Integers with Unlike Signs
To add two integers with unlike signs, proceed as follows:
- Subtract the smaller magnitude from the larger magnitude.
- Prefix the sign of the number with the larger magnitude.
For example, to find the sum −8 + 4 of Example 4, we would note that the integers −8 and 4 have magnitudes 8 and 4, respectively. We would then apply the process outlined in “Adding Two Integers with Unlike Signs.”
- Subtract the smaller magnitude from the larger magnitude; that is, 8 − 4 = 4.
- Prefix the sign of the number with the larger magnitude. Because −8 has the larger magnitude and its sign is negative, we prefix a negative sign to the difference of the magnitudes. Thus, −8+4= −4.
Example 5
Find the sums: (a) 5+ (−8), (b) −12+ 16, and (c) −117+115.
Solution
We’ll examine three separate but equivalent approaches, as discussed in the narrative above.
a) The number line schematic
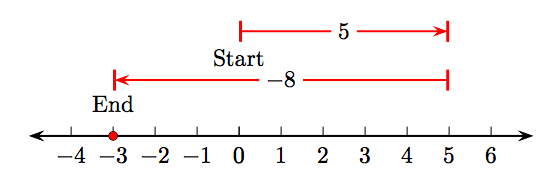
shows that 5 + (−8) = −3.
b) Drawing on physical intuition, start at zero, walk 12 units to the left, then turn around and walk 16 units to the right. You should find yourself 4 units to the right of the origin (zero). Hence, −12 + 16 = 4.
c) Following the algorithm in “Adding Two Integers with Unlike Signs,” subtract the smaller magnitude from the larger magnitude, thus 117−115 = 2. Because −117 has the larger magnitude and its sign is negative, we prefix a negative sign to the difference of the magnitudes. Thus, −117 + 115 = −2.
Exercise
Use a number line diagram to show the sum 5 + (−11).
- Answer
-
−6
Properties of Addition of Integers
You will be pleased to learn that the properties of addition for whole numbers also apply to addition of integers.
The Commutative Property of Addition
Let a and b represent two integers. Then,
\[a + b = b + a.\nonumber \]
Example 6
Show that 5 + (−7) = −7 + 5.
Solution
The number line schematic
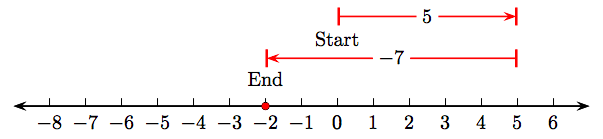
shows that 5 + (−7) = −2. On the other hand, the number line schematic
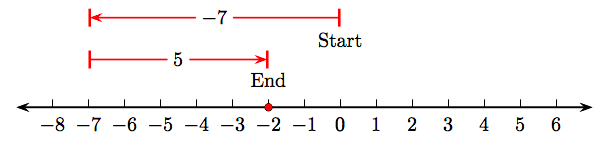
shows that −7+5= −2. Therefore, 5 + (−7) = −7 + 5.
Exercise
Use a number line diagram to show that −8 + 6 is the same as 6 + (−8).
Addition of integers is also associative.
The Associative Property of Addition
Let a, b, and c represent integers. Then,
\[(a + b) + c = a + (b + c)\nonumber \].
Example 7
Show that (−9 + 6) + 2 = −9 + (6 + 2).
Solution
On the left, the grouping symbols demand that we add −9 and 6 first. Thus,
\[ \begin{aligned} (−9 + 6) + 2 & = −3+2 \\ ~ & = −1. \end{aligned}\nonumber \]
On the right, the grouping symbols demand that we add 6 and 2 first. Thus,
\[ \begin{aligned} −9 + (6 + 2) & = −9+8 \\ ~ & = −1. \end{aligned}\nonumber \]
Both sides simplify to −1. Therefore, (−9 + 6) + 2 = −9 + (6 + 2).
Exercise
Show that the expression (−8 + 5) + 3 is the same as −8 + (5 + 3) by simplifying each of the two expressions independently.
The Additive Identity Property
The integer zero is called the additive identity. If a is any integer, then
a +0= a and 0 + a = a.
Thus, for example, −8+0= −8 and 0 + (−113) = −113.
Finally, every integer has a unique opposite, called its additive inverse.
The Additive Inverse Property
Let a represent any integer. Then there is a unique integer −a, called the opposite or additive inverse of a, such that
a + (−a) = 0 and −a + a = 0.
Example 8
Show that 5 + (−5) = 0.
Solution
The number line schematic
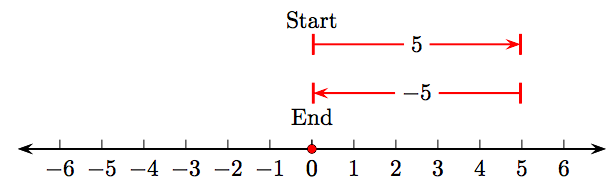
clearly shows that 5 + (−5) = 0.
Exercise
Use a number line diagram to show that 9 + (−9) = 0.
Important Observation
We have used several equivalent phrases to pronounce the integer −a. We’ve used “the opposite of a,” ”negative a,” and “the additive inverse of a.” All are equivalent pronunciations.
Grouping for Efficiency
Order of operations require that we perform all additions as they occur, working from left to right.
Example 9
Simplify −7+8+(−9) + 12.
Solution
We perform the additions as they occur, working left to right.
\[ \begin{aligned} =7 + 8 + (-9) +12 = 1 + (-9) +12 ~ & \textcolor{red}{ \text{ Working left to right, } -7 + 8 = 1.} \\ = -8 + 12 ~ & \textcolor{red}{ \text{ Working left to right, } 1 + (-9_ = -8.} \\ =4 ~ & \textcolor{red}{ ~ -8 + 12 = 4} \end{aligned}\nonumber \]
Thus, −7+8+(−9) + 12 = 4.
Exercise
Simplify: −8+9+(−4) + 2.
- Answer
-
−1
The commutative property of addition tells us that changing the order of addition does not change the answer. The associative property of addition tells us that a sum is not affected by regrouping. Let’s work Example 9 again, first grouping positive and negative numbers together.
Example 10
Simplify −7+8+(−9) + 12.
Solution
The commutative and associative properties allows us to change the order of addition and regroup.
\[ \begin{aligned} -7 + 8 + (-9) + 12 = -7 + (-9) + 8 + 12 ~ & \textcolor{red}{ \text{ Use the commutative property to change the order.}} \\ = [-7+(-9)] + [8+12] ~ & \textcolor{red}{ \text{ Use the associative property to regroup.}} \\ =-16 + 20 ~ & \textcolor{red}{ \text{ Add the negatives. Add the positives.}} \\ =4 ~ & \textcolor{red}{ \text{ One final addition.}} \end{aligned}\nonumber \]
Thus, −7+8+(−9) + 12 = 4.
Exercise
Simplify: −11 + 7 + (−12) + 3.
- Answer
-
−13
At first glance, there seems to be no advantage in using the technique in Example 10 over the technique used in Example 9. However, the technique in Example 10 is much quicker in practice, particularly if you eliminate some of the explanatory steps.
Efficient Grouping
When asked to find the sum of a number of integers, it is most efficient to first add all the positive integers, then add the negatives, then add the results.
Example 11
Simplify −7+8+(−9) + 12.
Solution
Add the positive integers first, then the negatives, then add the results.
\[ \begin{aligned} -7 + 8 + (-9) +12 = 20 + (-16) ~ & \textcolor{red}{ \text{ Add the positives: } 8 + 12 = 20.} \\ ~ & \textcolor{red}{ \text{ Add the negatives: } -7 + (-9) = -16.} \\ =4 ~ & \textcolor{red}{ \text{ Add the results: } 20 + (-16) = 4.} \end{aligned}\nonumber \]
Thus, −7+8+(−9) + 12 = 4.
Exercise
Simplify: −11 + 3 + (−2) + 7.
- Answer
-
−3
Using Correct Notation
Never write +−! That is, the notation
9 +−4 and − 8 +−6
should not be used. Instead, use grouping symbols as follows:
9+(−4) and −8+(−6)
Exercises
In Exercises 1-12, what integer is represented by the given vector?
1.
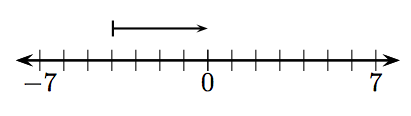
2.
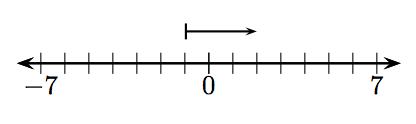
3.
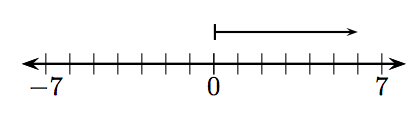
4.

5.
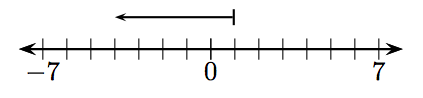
6.
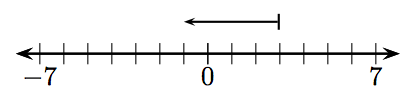
7.
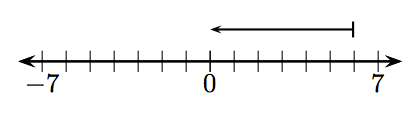
8.
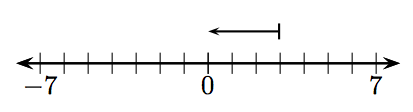
9.
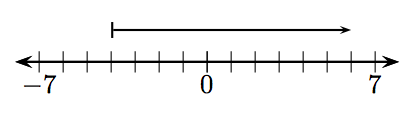
10.
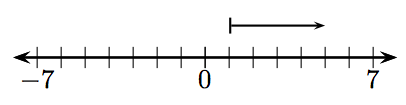
11.
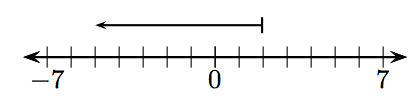
12.
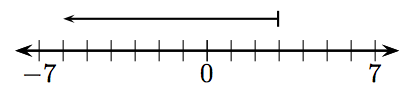
In Exercises 13-36, find the sum of the given integers.
13. −15 + 1
14. −1 + 18
15. 18 + (−10)
16. 2+(−19)
17. −10 + (−12)
18. −1+(−7)
19. 5 + 10
20. 1 + 12
21. 2+5
22. 14 + 1
23. 19 + (−15)
24. 20 + (−17)
25. −2+(−7)
26. −14 + (−6)
27. −6 + 16
28. −2 + 14
29. −11 + (−6)
30. −7+(−8)
31. 14 + (−9)
32. 5+(−15)
33. 10 + 11
34. 14 + 11
35. −13 + 1
36. −8+2
In Exercises 37-52, state the property of addition depicted by the given identity.
37. −1 + (3 + (−8)) = (−1 + 3) + (−8)
38. −4 + (6 + (−5)) = (−4 + 6) + (−5)
39. 7+(−7) = 0
40. 14 + (−14) = 0
41. 15 + (−18) = −18 + 15
42. 14 + (−8) = −8 + 14
43. −15 + 0 = −15
44. −11 + 0 = −11
45. −7 + (1 + (−6)) = (−7 + 1) + (−6)
46. −4 + (8 + (−1)) = (−4 + 8) + (−1)
47. 17 + (−2) = −2 + 17
48. 5+(−13) = −13 + 5
49. −4+0= −4
50. −7+0= −7
51. 19 + (−19) = 0
52. 5+(−5) = 0
In Exercises 53-64, state the additive inverse of the given integer.
53. 18
54. 10
55. 12
56. 15
57. −16
58. −4
59. 11
60. 13
61. −15
62. −19
63. −18
64. −9
In Exercises 65-80, find the sum of the given integers.
65. 6+(−1) + 3 + (−4)
66. 6+(−3) + 2 + (−7)
67. 15 + (−1) + 2
68. 11 + (−16) + 16
69. −17 + 12 + 3
70. −5+(−3) + 2
71. 7 + 20 + 19
72. 14 + (−14) + (−20)
73. 4+(−8) + 2 + (−5)
74. 6+(−3) + 7 + (−2)
75. 7+(−8) + 2 + (−1)
76. 8+(−9) + 5 + (−3)
77. 9+(−3) + 4 + (−1)
78. 1+(−9) + 7 + (−6)
79. 9 + 10 + 2
80. −6 + 15 + (−18)
81. Bank Account. Gerry opened a new bank account, depositing a check for $215. He then made several withdraws of $40, $75, and $20 before depositing another check for $185. How much is in Gerry’s account now?
82. Dead Sea Sinking. Due to tectonic plate movement, the Dead Sea is sinking about 1 meter each year. If it’s currently −418 meters now, what will Dead Sea elevation be in 5 years? Write an expression that models this situation and compute the result.
83. Profit and Loss. Profits and losses for the first six months of the fiscal year for a small business are shown in the following bar chart. Sum the profits and losses from each month. Was there a net profit or loss over the six-month period? How much?
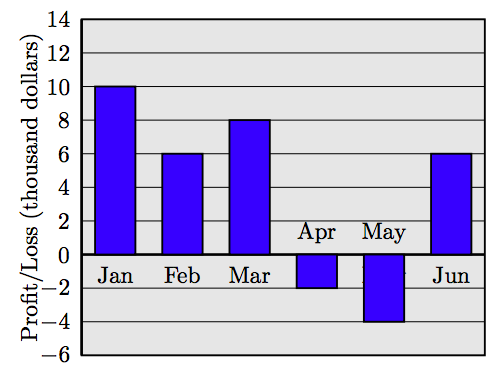
84. Profit and Loss. Profits and losses for the first six months of the fiscal year for a small business are shown in the following bar chart. Sum the profits and losses from each month. Was there a net profit or loss over the six-month period? How much?
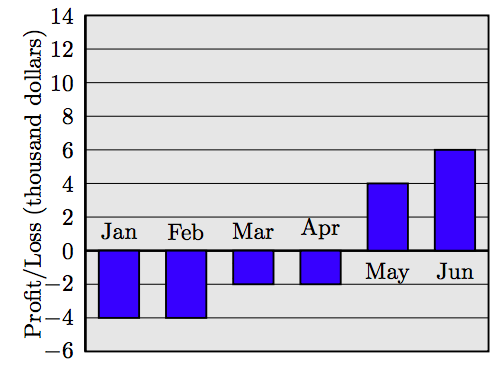
Answers
1. 4
3. 6
5. −5
7. −6
9. 10
11. −7
13. −14
15. 8
17. −22
19. 15
21. 7
23. 4
25. −9
27. 10
29. −17
31. 5
33. 21
35. −12
37. Associative property of addition
39. Additive inverse property
41. Commutative property of addition
43. Additive identity property
45. Associative property of addition
47. Commutative property of addition
49. Additive identity property
51. Additive inverse property
53. −18
55. −12
57. 16
59. −11
61. 15
63. 18
65. 4
67. 16
69. −2
71. 46
73. −7
75. 0
77. 9
79. 21
81. $265
83. Net Profit: $24,000


