3.7: Add and Subtract Fractions with Different Denominators (Part 2)
- Page ID
- 57370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify and Use Fraction Operations
By now in this chapter, you have practiced multiplying, dividing, adding, and subtracting fractions. The following table summarizes these four fraction operations. Remember: You need a common denominator to add or subtract fractions, but not to multiply or divide fractions.
Fraction multiplication: Multiply the numerators and multiply the denominators.
\[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]
Fraction division: Multiply the first fraction by the reciprocal of the second.
\[\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\]
Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\]
Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
\[\dfrac{a}{c} - \dfrac{a}{c} = \dfrac{a - b}{c}\]
Simplify:
- \(− \dfrac{1}{4} + \dfrac{1}{6}\)
- \(− \dfrac{1}{4} \div \dfrac{1}{6}\)
Solution
First we ask ourselves, “What is the operation?”
- The operation is addition. Do the fractions have a common denominator? No.
| Find the LCD. |  |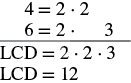
| Rewrite each fraction as an equivalent fraction with the LCD. | \(- \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \) |
| Simplify the numerators and denominators. | \(- \dfrac{3}{12} + \dfrac{2}{12} \) |
| Add the numerators and place the sum over the common denominator. | \(- \dfrac{1}{12} \) |
| Check to see if the answer can be simplified. It cannot. |
- The operation is division. We do not need a common denominator.
| To divide fractions, multiply the first fraction by the reciprocal of the second. | \(- \dfrac{1}{4} \cdot \dfrac{6}{1}\) |
| Multiply. | \(- \dfrac{6}{4}\) |
| Simplify. | \(- \dfrac{3}{2} \) |
Simplify:
- \(− \dfrac{3}{4} - \dfrac{1}{6}\)
- \(− \dfrac{3}{4} \cdot \dfrac{1}{6}\)
- Answer a
-
\(-\dfrac{11}{12}\)
- Answer b
-
\(-\dfrac{1}{8}\)
Simplify:
- \(\dfrac{5}{6} \div \left(- \dfrac{1}{4}\right)\)
- \(\dfrac{5}{6} - \left(- \dfrac{1}{4}\right)\)
- Answer a
-
\(-\dfrac{10}{3}\)
- Answer b
-
\(\dfrac{13}{12}\)
Simplify:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6} \cdot \dfrac{3}{10}\)
Solution
- The operation is subtraction. The fractions do not have a common denominator.
| Rewrite each fraction as an equivalent fraction with the LCD, 30. | \(\dfrac{5x \cdot \textcolor{red}{5}}{6 \cdot \textcolor{red}{5}} - \dfrac{3 \cdot \textcolor{red}{3}}{10 \cdot \textcolor{red}{3}} \) |
| \(\dfrac{25x}{30} - \dfrac{9}{30} \) | |
| Subtract the numerators and place the difference over the common denominator. | \(\dfrac{25x - 9}{30} \) |
- The operation is multiplication; no need for a common denominator.
| To multiply fractions, multiply the numerators and multiply the denominators. | \(\dfrac{5x \cdot 3}{ 6 \cdot 10} \) |
| Rewrite, showing common factors. | \(\dfrac{\cancel{5} \cdot x \cdot \cancel{3}}{2 \cdot \cancel{3} \cdot 2 \cdot \cancel{5}} \) |
| Remove common factors to simplify. | \(\dfrac{x}{4} \) |
Simplify:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4} \cdot \dfrac{8}{9}\)
- Answer a
-
\(\dfrac{27a-32}{36}\)
- Answer b
-
\(\dfrac{2a}{3}\)
Simplify:
- \(\dfrac{4k}{5} + \dfrac{5}{6}\)
- \(\dfrac{4k}{5} \div \dfrac{5}{6}\)
- Answer a
-
\(\dfrac{24k+25}{30}\)
- Answer b
-
\(\dfrac{24k}{25}\)
Use the Order of Operations to Simplify Complex Fractions
In Multiply and Divide Mixed Numbers and Complex Fractions, we saw that a complex fraction is a fraction in which the numerator or denominator contains a fraction. We simplified complex fractions by rewriting them as division problems. For example,
\[\dfrac{\dfrac{3}{4}}{\dfrac{5}{8}} = \dfrac{3}{4} \div \dfrac{5}{8} \nonumber \]
Now we will look at complex fractions in which the numerator or denominator can be simplified. To follow the order of operations, we simplify the numerator and denominator separately first. Then we divide the numerator by the denominator.
Step 1. Simplify the numerator.
Step 2. Simplify the denominator.
Step 3. Divide the numerator by the denominator.
Step 4. Simplify if possible.
Simplify: \(\dfrac{\left(\dfrac{1}{2}\right)^{2}}{4 + 3^{2}}\).
Solution
| Simplify the numerator. | \(\dfrac{\dfrac{1}{4}}{4 + 3^{2}}\) |
| Simplify the term with the exponent in the denominator. | \(\dfrac{\dfrac{1}{4}}{4 + 9} \) |
| Add the terms in the denominator. | \(\dfrac{\dfrac{1}{4}}{13} \) |
| Divide the numerator by the denominator. | \(\dfrac{1}{4} \div 13 \) |
| Rewrite as multiplication by the reciprocal. | \(\dfrac{1}{4} \cdot \dfrac{1}{13} \) |
| Multiply. | \(\dfrac{1}{52}\) |
Simplify: \(\dfrac{\left(\dfrac{1}{3}\right)^{2}}{2^{3} + 2}\).
- Answer
-
\(\dfrac{1}{90}\)
Simplify: \(\dfrac{1 + 4^{2}}{\left(\dfrac{1}{4}\right)^{2}}\).
- Answer
-
\(272\)
Simplify: \(\dfrac{\dfrac{1}{2} + \dfrac{2}{3}}{\dfrac{3}{4} - \dfrac{1}{6}}\).
Solution
| Rewrite numerator with the LCD of 6 and denominator with LCD of 12. | \(\dfrac{\dfrac{3}{6} + \dfrac{4}{6}}{\dfrac{9}{12} - \dfrac{2}{12}} \) |
| Add in the numerator. Subtract in the denominator. | \(\dfrac{\dfrac{7}{6}}{\dfrac{7}{12}} \) |
| Divide the numerator by the denominator. | \(\dfrac{7}{6} \div \dfrac{7}{12}\) |
| Rewrite as multiplication by the reciprocal. | \(\dfrac{7}{6} \cdot \dfrac{12}{7} \) |
| Rewrite, showing common factors. | \(\dfrac{\cancel{7} \cdot \cancel{6} \cdot 2}{\cancel{6} \cancel{7} \cdot 1} \) |
| Simplify. | \(2 \) |
Simplify: \(\dfrac{\dfrac{1}{3} + \dfrac{1}{2}}{\dfrac{3}{4} - \dfrac{1}{3}}\).
- Answer
-
\(2\)
Simplify: \(\dfrac{\dfrac{2}{3} - \dfrac{1}{2}}{\dfrac{1}{4} + \dfrac{1}{3}}\).
- Answer
-
\(\dfrac{2}{7}\)
Evaluate Variable Expressions with Fractions
We have evaluated expressions before, but now we can also evaluate expressions with fractions. Remember, to evaluate an expression, we substitute the value of the variable into the expression and then simplify.
Evaluate \(x + \dfrac{1}{3}\) when
- \(x = - \dfrac{1}{3}\)
- \(x = - \dfrac{3}{4}\)
Solution
- To evaluate \(x + \dfrac{1}{3}\) when \(x = − \dfrac{1}{3}\), substitute \(− \dfrac{1}{3}\) for \(x\) in the expression.
| Substitute \(\textcolor{red}{- \dfrac{1}{3}}\) for x. | \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3} \) |
| Simplify. | \(0 \) |
- To evaluate \(x + \dfrac{1}{3}\) when \(x = − \dfrac{3}{4}\), we substitute \(− \dfrac{3}{4}\) for \(x\) in the expression.
| Substitute \(\textcolor{red}{- \dfrac{3}{4}}\) for x. | \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3}\) |
| Rewrite as equivalent fractions with the LCD, 12. | \(- \dfrac{3 \cdot 3}{4 \cdot 3} + \dfrac{1 \cdot 4}{3 \cdot 4} \) |
| Simplify the numerators and denominators. | \(- \dfrac{9}{12} + \dfrac{4}{12} \) |
| Add. | \(- \dfrac{5}{12} \) |
Evaluate \(x + \dfrac{3}{4}\) when:
- \(x = - \dfrac{7}{4}\)
- \(x = - \dfrac{5}{4}\)
- Answer a
-
\(-1\)
- Answer b
-
\(-\dfrac{1}{2}\)
Evaluate \(y + \dfrac{1}{2}\) when:
- \(y = \dfrac{2}{3}\)
- \(y = - \dfrac{3}{4}\)
- Answer a
-
\(\dfrac{7}{6}\)
- Answer b
-
\(-\dfrac{1}{4}\)
Evaluate \(y − \dfrac{5}{6}\) when \(y = - \dfrac{2}{3}\).
Solution
We substitute \(− \dfrac{2}{3}\) for \(y\) in the expression.
| Substitute \(\textcolor{red}{- \dfrac{2}{3}}\) for y. | \(\textcolor{red}{- \dfrac{2}{3}} - \dfrac{5}{6}\) |
| Rewrite as equivalent fractions with the LCD, 6. | \(- \dfrac{4}{6} - \dfrac{5}{6} \) |
| Subtract. | \(- \dfrac{9}{6} \) |
| Simplify. | \(- \dfrac{3}{2} \) |
Evaluate \(y − \dfrac{1}{2}\) when \(y = - \dfrac{1}{4}\).
- Answer
-
\(-\dfrac{3}{4}\)
Evaluate \(x − \dfrac{3}{8}\) when \(x = - \dfrac{5}{2}\).
- Answer
-
\(-\dfrac{23}{8}\)
Evaluate \(2x^2y\) when \(x = \dfrac{1}{4}\) and \(y = − \dfrac{2}{3}\).
Solution
Substitute the values into the expression. In \(2x^2y\), the exponent applies only to \(x\).
| Substitute \(\textcolor{red}{\dfrac{1}{4}}\) for x and \(\textcolor{blue}{- \dfrac{2}{3}}\) for y. | \(2 \left(\textcolor{red}{\dfrac{1}{4}}\right)^{2} \left(\textcolor{blue}{- \dfrac{2}{3}}\right) \) |
| Simplify exponents first. | \(2 \left(\dfrac{1}{16}\right) \left(- \dfrac{2}{3}\right)\) |
| Multiply. The product will be negative. | \(- \dfrac{2}{1} \cdot \dfrac{1}{16} \cdot \dfrac{2}{3} \) |
| Simplify. | \(- \dfrac{4}{48} \) |
| Remove the common factors. | \(- \dfrac{1 \cdot \cancel{4}}{\cancel{4} \cdot 12} \) |
| Simplify. | \(- \dfrac{1}{12} \) |
Evaluate: \(3ab^2\) when \(a = − \dfrac{2}{3}\) and \(b = − \dfrac{1}{2}\).
- Answer
-
\(-\dfrac{1}{2}\)
Evaluate: \(4c^3d\) when \(c = − \dfrac{1}{2}\) and \(d = − \dfrac{4}{3}\).
- Answer
-
\(\dfrac{2}{3}\)
Evaluate: \(\dfrac{p + q}{r}\) when \(p = −4\), \(q = −2\), and \(r = 8\).
Solution
We substitute the values into the expression and simplify.
| Substitute \(\textcolor{red}{-4}\) for p, \(\textcolor{blue}{-2}\) for q and \(\textcolor{magenta}{8}\) for r. | \(\dfrac{\textcolor{red}{-4} + \textcolor{blue}{(-2)}}{\textcolor{magenta}{8}} \) |
| Add in the numerator first. | \(- \dfrac{6}{8}\) |
| Simplify. | \(- \dfrac{3}{4}\) |
Evaluate: \(\dfrac{a + b}{c}\) when \(a = −8\), \(b = −7\), and \(c = 6\).
- Answer
-
\(-\dfrac{5}{2}\)
Evaluate: \(\dfrac{x + y}{z}\) when \(x = 9\), \(y = −18\), and \(z =- 6\).
- Answer
-
\(\dfrac{3}{2}\)
Practice Makes Perfect
Find the Least Common Denominator (LCD)
In the following exercises, find the least common denominator (LCD) for each set of fractions.
- \(\dfrac{2}{3}\) and \(\dfrac{3}{4}\)
- \(\dfrac{3}{4}\) and \(\dfrac{2}{5}\)
- \(\dfrac{7}{12}\) and \(\dfrac{5}{8}\)
- \(\dfrac{9}{16}\) and \(\dfrac{7}{12}\)
- \(\dfrac{13}{30}\) and \(\dfrac{25}{42}\)
- \(\dfrac{23}{30}\) and \(\dfrac{5}{48}\)
- \(\dfrac{21}{35}\) and \(\dfrac{39}{56}\)
- \(\dfrac{18}{35}\) and \(\dfrac{33}{49}\)
- \(\dfrac{2}{3}, \dfrac{1}{6}\) and \(\dfrac{3}{4}\)
- \(\dfrac{2}{3}, \dfrac{1}{4}\) and \(\dfrac{3}{5}\)
Convert Fractions to Equivalent Fractions with the LCD
In the following exercises, convert to equivalent fractions using the LCD.
- \(\dfrac{1}{3}\) and \(\dfrac{1}{4}\), LCD = 12
- \(\dfrac{1}{4}\) and \(\dfrac{1}{5}\), LCD = 20
- \(\dfrac{5}{12}\) and \(\dfrac{7}{8}\), LCD = 24
- \(\dfrac{7}{12}\) and \(\dfrac{5}{8}\), LCD = 24
- \(\dfrac{13}{16}\) and \(- \dfrac{11}{12}\), LCD = 48
- \(\dfrac{11}{16}\) and \(- \dfrac{5}{12}\), LCD = 48
- \(\dfrac{1}{3}, \dfrac{5}{6}\), and \(\dfrac{3}{4}\), LCD = 12
- \(\dfrac{1}{3}, \dfrac{3}{4}\), and \(\dfrac{3}{5}\), LCD = 60
Add and Subtract Fractions with Different Denominators
In the following exercises, add or subtract. Write the result in simplified form.
- \(\dfrac{1}{3} + \dfrac{1}{5}\)
- \(\dfrac{1}{4} + \dfrac{1}{5}\)
- \(\dfrac{1}{2} + \dfrac{1}{7}\)
- \(\dfrac{1}{3} + \dfrac{1}{8}\)
- \(\dfrac{1}{3} - \left(- \dfrac{1}{9}\right)\)
- \(\dfrac{1}{4} - \left(- \dfrac{1}{8}\right)\)
- \(\dfrac{1}{5} - \left(- \dfrac{1}{10}\right)\)
- \(\dfrac{1}{2} - \left(- \dfrac{1}{6}\right)\)
- \(\dfrac{2}{3} + \dfrac{3}{4}\)
- \(\dfrac{3}{4} + \dfrac{2}{5}\)
- \(\dfrac{7}{12} + \dfrac{5}{8}\)
- \(\dfrac{5}{12} + \dfrac{3}{8}\)
- \(\dfrac{7}{12} - \dfrac{9}{16}\)
- \(\dfrac{7}{16} - \dfrac{5}{12}\)
- \(\dfrac{11}{12} - \dfrac{3}{8}\)
- \(\dfrac{5}{8} - \dfrac{7}{12}\)
- \(\dfrac{2}{3} - \dfrac{3}{8}\)
- \(\dfrac{5}{6} - \dfrac{3}{4}\)
- \(− \dfrac{11}{30} + \dfrac{27}{40}\)
- \(− \dfrac{9}{20} + \dfrac{17}{30}\)
- \(− \dfrac{13}{30} + \dfrac{25}{42}\)
- \(− \dfrac{23}{30} + \dfrac{5}{48}\)
- \(− \dfrac{39}{56} - \dfrac{22}{35}\)
- \(− \dfrac{33}{49} - \dfrac{18}{35}\)
- \(- \dfrac{2}{3} - \left(- \dfrac{3}{4}\right)\)
- \(- \dfrac{3}{4} - \left(- \dfrac{4}{5}\right)\)
- \(- \dfrac{9}{16} - \left(- \dfrac{4}{5}\right)\)
- \(- \dfrac{7}{20} - \left(- \dfrac{5}{8}\right)\)
- 1 + \(\dfrac{7}{8}\)
- 1 + \(\dfrac{5}{6}\)
- 1 − \(\dfrac{5}{9}\)
- 1 − \(\dfrac{3}{10}\)
- \(\dfrac{x}{3} + \dfrac{1}{4}\)
- \(\dfrac{y}{2} + \dfrac{2}{3}\)
- \(\dfrac{y}{4} - \dfrac{3}{5}\)
- \(\dfrac{x}{5} - \dfrac{1}{4}\)
Identify and Use Fraction Operations
In the following exercises, perform the indicated operations. Write your answers in simplified form.
- (a) \(\dfrac{3}{4} + \dfrac{1}{6}\) (b) \(\dfrac{3}{4} \div \dfrac{1}{6}\)
- (a) \(\dfrac{2}{3} + \dfrac{1}{6}\) (b) \(\dfrac{2}{3} \div \dfrac{1}{6}\)
- (a) \(- \dfrac{2}{5} - \dfrac{1}{8}\) (b) \(- \dfrac{2}{5} \cdot \dfrac{1}{8}\)
- (a) \(- \dfrac{4}{5} - \dfrac{1}{8}\) (b) \(- \dfrac{4}{5} \cdot \dfrac{1}{8}\)
- (a) \(\dfrac{5n}{6} \div \dfrac{8}{15}\) (b) \(\dfrac{5n}{6} - \dfrac{8}{15}\)
- (a) \(\dfrac{3a}{8} \div \dfrac{7}{12}\) (b) \(\dfrac{3a}{8} - \dfrac{7}{12}\)
- (a) \(\dfrac{9}{10} \cdot \left(− \dfrac{11d}{12}\right)\) (b) \(\dfrac{9}{10} + \left(− \dfrac{11d}{12}\right)\)
- (a) \(\dfrac{4}{15} \cdot \left(− \dfrac{5}{q}\right)\) (b) \(\dfrac{4}{15} + \left(− \dfrac{5}{q}\right)\)
- \(- \dfrac{3}{8} \div \left(- \dfrac{3}{10}\right)\)
- \(- \dfrac{5}{12} \div \left(- \dfrac{5}{9}\right)\)
- \(- \dfrac{3}{8} + \dfrac{5}{12}\)
- \(- \dfrac{1}{8} + \dfrac{7}{12}\)
- \(\dfrac{5}{6} − \dfrac{1}{9}\)
- \(\dfrac{5}{9} − \dfrac{1}{6}\)
- \(\dfrac{3}{8} \cdot \left(− \dfrac{10}{21}\right)\)
- \(\dfrac{7}{12} \cdot \left(− \dfrac{8}{35}\right)\)
- \(− \dfrac{7}{15} - \dfrac{y}{4}\)
- \(− \dfrac{3}{8} - \dfrac{x}{11}\)
- \(\dfrac{11}{12a} \cdot \dfrac{9a}{16}\)
- \(\dfrac{10y}{13} \cdot \dfrac{8}{15y}\)
Use the Order of Operations to Simplify Complex Fractions
In the following exercises, simplify.
- \(\dfrac{\left(\dfrac{1}{5} \right)^{2}}{2 + 3^{2}}\)
- \(\dfrac{\left(\dfrac{1}{3} \right)^{2}}{5 + 2^{2}}\)
- \(\dfrac{2^{3} + 4^{2}}{\left(\dfrac{2}{3}\right)^{2}}\)
- \(\dfrac{3^{3} - 3^{2}}{\left(\dfrac{3}{4}\right)^{2}}\)
- \(\dfrac{\left(\dfrac{3}{5} \right)^{2}}{\left(\dfrac{3}{7}\right)^{2}}\)
- \(\dfrac{\left(\dfrac{3}{4} \right)^{2}}{\left(\dfrac{5}{8}\right)^{2}}\)
- \(\dfrac{2}{\dfrac{1}{3} + \dfrac{1}{5}}\)
- \(\dfrac{5}{\dfrac{1}{4} + \dfrac{1}{3}}\)
- \(\dfrac{\dfrac{2}{3} + \dfrac{1}{2}}{\dfrac{3}{4} - \dfrac{2}{3}}\)
- \(\dfrac{\dfrac{3}{4} + \dfrac{1}{2}}{\dfrac{5}{6} - \dfrac{2}{3}}\)
- \(\dfrac{\dfrac{7}{8} - \dfrac{2}{3}}{\dfrac{1}{2} + \dfrac{3}{8}}\)
- \(\dfrac{\dfrac{3}{4} - \dfrac{3}{5}}{\dfrac{1}{4} + \dfrac{2}{5}}\)
Mixed Practice
In the following exercises, simplify.
- \(\dfrac{1}{2} + \dfrac{2}{3} \cdot \dfrac{5}{12}\)
- \(\dfrac{1}{3} + \dfrac{2}{5} \cdot \dfrac{3}{4}\)
- 1 − \(\dfrac{3}{5} \div \dfrac{1}{10}\)
- 1 − \(\dfrac{5}{6} \div \dfrac{1}{12}\)
- \(\dfrac{2}{3} + \dfrac{1}{6} + \dfrac{3}{4}\)
- \(\dfrac{2}{3} + \dfrac{1}{4} + \dfrac{3}{5}\)
- \(\dfrac{3}{8} - \dfrac{1}{6} + \dfrac{3}{4}\)
- \(\dfrac{2}{5} + \dfrac{5}{8} - \dfrac{3}{4}\)
- 12\(\left(\dfrac{9}{20} − \dfrac{4}{15}\right)\)
- 8\(\left(\dfrac{15}{16} − \dfrac{5}{6}\right)\)
- \(\dfrac{\dfrac{5}{8} + \dfrac{1}{6}}{\dfrac{19}{24}}\)
- \(\dfrac{\dfrac{1}{6} + \dfrac{3}{10}}{\dfrac{14}{30}}\)
- \(\left(\dfrac{5}{9} + \dfrac{1}{6}\right) \div \left(\dfrac{2}{3} − \dfrac{1}{2}\right)\)
- \(\left(\dfrac{3}{4} + \dfrac{1}{6}\right) \div \left(\dfrac{5}{8} − \dfrac{1}{3}\right)\)
In the following exercises, evaluate the given expression. Express your answers in simplified form, using improper fractions if necessary.
- x + \(\dfrac{1}{2}\) when
- x = \(− \dfrac{1}{8}\)
- x = \(− \dfrac{1}{2}\)
- x + \(\dfrac{2}{3}\) when
- x = \(− \dfrac{1}{6}\)
- x = \(− \dfrac{5}{3}\)
- x + \(\left(− \dfrac{5}{6}\right)\) when
- x = \(\dfrac{1}{3}\)
- x = \(− \dfrac{1}{6}\)
- x + \(\left(− \dfrac{11}{12}\right)\) when
- x = \(\dfrac{11}{12}\)
- x = \(\dfrac{3}{4}\)
- x − \(\dfrac{2}{5}\) when
- x = \(\dfrac{3}{5}\)
- x = \(- \dfrac{3}{5}\)
- x − \(\dfrac{1}{3}\) when
- x = \(\dfrac{2}{3}\)
- x = \(- \dfrac{2}{3}\)
- \(\dfrac{7}{10}\) − w when
- w = \(\dfrac{1}{2}\)
- w = \(- \dfrac{1}{2}\)
- \(\dfrac{5}{12}\) − w when
- w = \(\dfrac{1}{4}\)
- w = \(- \dfrac{1}{4}\)
- 4p2q when p = \(- \dfrac{1}{2}\) and q = \(\dfrac{5}{9}\)
- 5m2n when m = \(- \dfrac{2}{5}\) and n = \(\dfrac{1}{3}\)
- 2x2y3 when x = \(- \dfrac{2}{3}\) and y = \(- \dfrac{1}{2}\)
- 8u2v3 when u = \(- \dfrac{3}{4}\) and v = \(- \dfrac{1}{2}\)
- \(\dfrac{u + v}{w}\) when u = −4, v = −8, w = 2
- \(\dfrac{m + n}{p}\) when m = −6, n = −2, p = 4
- \(\dfrac{a + b}{a - b}\) when a = −3, b = 8
- \(\dfrac{r - s}{r + s}\) when r = 10, s = −5
Everyday Math
- Decorating Laronda is making covers for the throw pillows on her sofa. For each pillow cover, she needs \(\dfrac{3}{16}\) yard of print fabric and \(\dfrac{3}{8}\) yard of solid fabric. What is the total amount of fabric Laronda needs for each pillow cover?
- Baking Vanessa is baking chocolate chip cookies and oatmeal cookies. She needs \(1 \dfrac{1}{4}\) cups of sugar for the chocolate chip cookies, and \(1 \dfrac{1}{8}\) cups for the oatmeal cookies How much sugar does she need altogether?
Writing Exercises
- Explain why it is necessary to have a common denominator to add or subtract fractions.
- Explain how to find the LCD of two fractions.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) After looking at the checklist, do you think you are well prepared for the next section? Why or why not?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."