9.3: Factoring of the Quadratic

We’ve seen how vertex form and intelligent use of the axis of symmetry can help to draw an accurate graph of the quadratic function defined by the equation \(f(x) = ax^2+bx+c\). When drawing the graph of the parabola it is helpful to know where the graph of the parabola crosses the x-axis. That is the primary goal of this section, to find the zero crossings or x-intercepts of the parabola.

Before we begin, you’ll need to review the techniques that will enable you to factor the quadratic expression \(ax^2 + bx + c\).

Factoring \(ax^2 + bx + c\) when a = 1

Our intent in this section is to provide a quick review of techniques used to factor quadratic trinomials. We begin by showing how to factor trinomials having the form \(ax^2 + bx + c\), where the leading coefficient is a = 1; that is, trinomials having the form \(x^2+bx+c\). In the next section, we will address the technique used to factor \(ax^2+bx+c\) when \(a \neq 1\).

Let’s begin with an example.

Example \(\PageIndex{1}\)

Factor \(x^{2}+16 x-36\)

Solution

Note that the leading coefficient, the coefficient of \(x^2\), is a 1. This is an important observation, because the technique presented here will not work when the leading coefficient does not equal 1.

Note the constant term of the trinomial \(x^2 + 16x − 36\) is −36. List all integer pairs whose product equals −36.

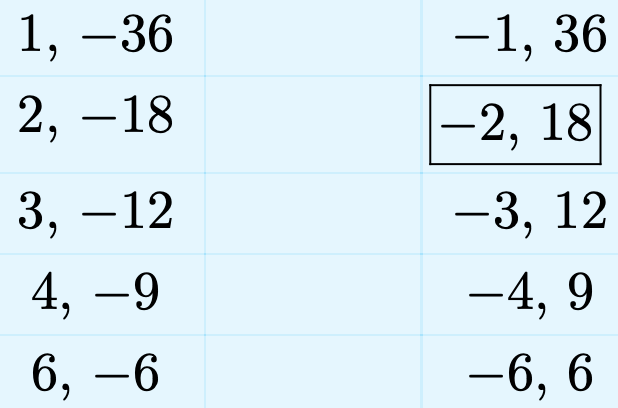
Note that we’ve framed the pair −2, 18. We’ve done this because the sum of this pair of integers equals the coefficient of x in the trinomial expression \(x^2 + 16x − 36\). Use this framed pair to factor the trinomial.

\[x^{2}+16 x-36=(x-2)(x+18)\]

It is important that you check your result. Use the distributive property to multiply.

\[\begin{aligned}(x-2)(x+18) &=x(x+18)-2(x+18) \\ &=x^{2}+18 x-2 x-36 \\ &=x^{2}+16 x-36 \end{aligned}\]

Thus, our factorization is correct.

Let’s summarize the technique.

Algorithm

To factor the quadratic \(x^2 + bx + c\), proceed as follows:

1. List all the integer pairs whose product equals c.
2. Circle or frame the pair whose sum equals the coefficient of x, namely b. Use this pair to factor the trinomial.

Let’s look at another example.

Example \(\PageIndex{2}\)

Factor the trinomial \(x^{2}-25 x-84\)

Solution

List all the integer pairs whose product is −84.

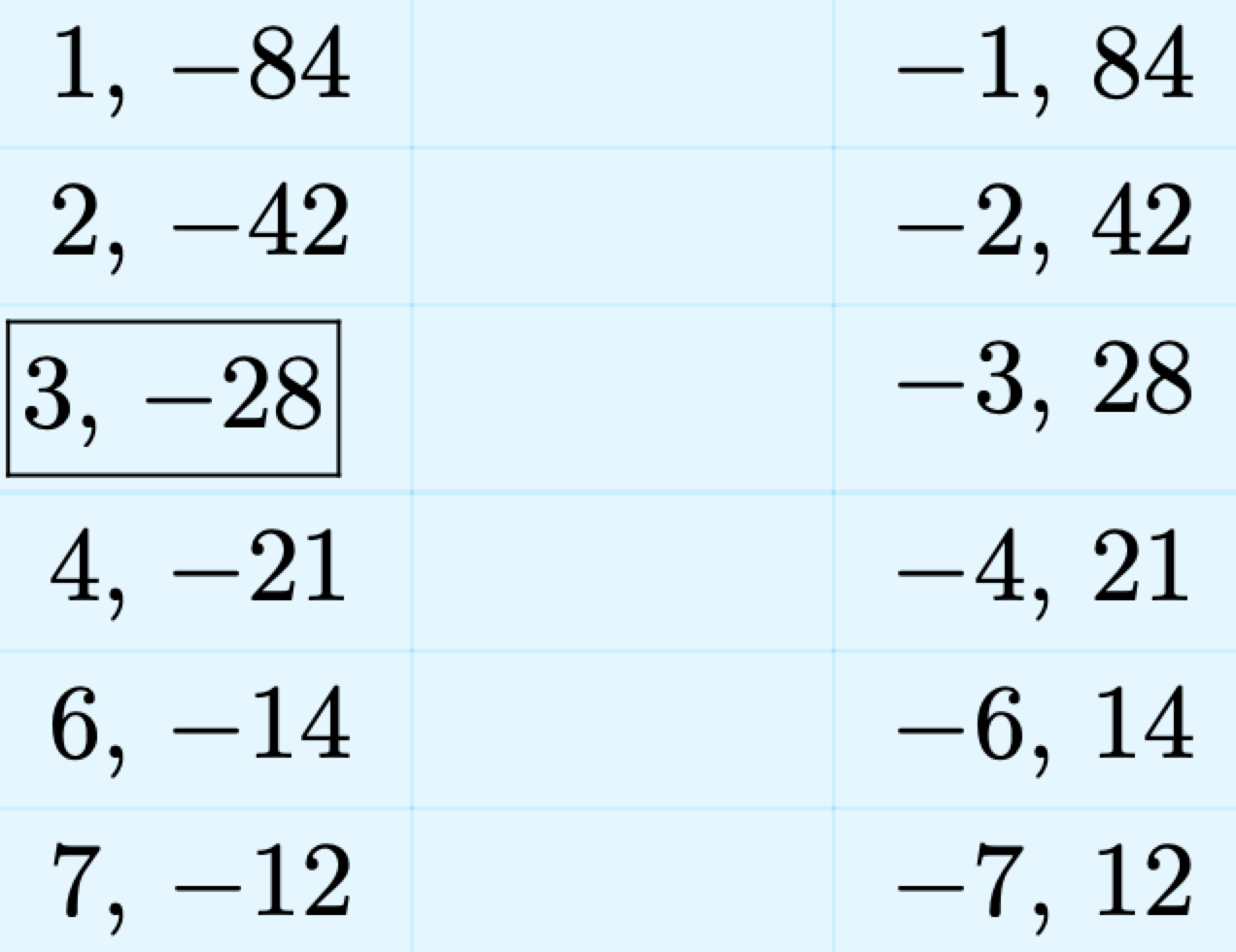
We’ve framed the pair whose sum equals the coefficient of x, namely −25. Use this pair to factor the trinomial.

\[x^{2}-25 x-84=(x+3)(x-28) \nonumber\]

Check

\[\begin{aligned}(x+3)(x-28) &=x(x-28)+3(x-28) \\ &=x^{2}-28 x+3 x-84 \\ &=x^{2}-25 x-84 \end{aligned}\]

With experience, there are a number of ideas that will quicken the process.

• As you are listing the integer pairs, should you happen to note that the current pair has the appropriate sum, there is no need to list the remaining integer pairs. Simply halt the process of listing the integer pairs and use the current pair to factor the trinomial.
• Some students are perfectly happy being asked “Can you think of an integer pair whose product is c and whose sum is b (where b and c refer to the coefficients of \(x^2 +bx+c\))?” If you can pick the pair “out of the air” like this, all is well and good.

Use the integer pair to factor the trinomial and don’t bother listing any integer pairs.

Intercepts

The points where the graph of a function crosses the x-axis are called the x-intercepts of graph of the function. Consider the graph of the quadratic function f in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): The x- and y-intercepts are key features of any graph.

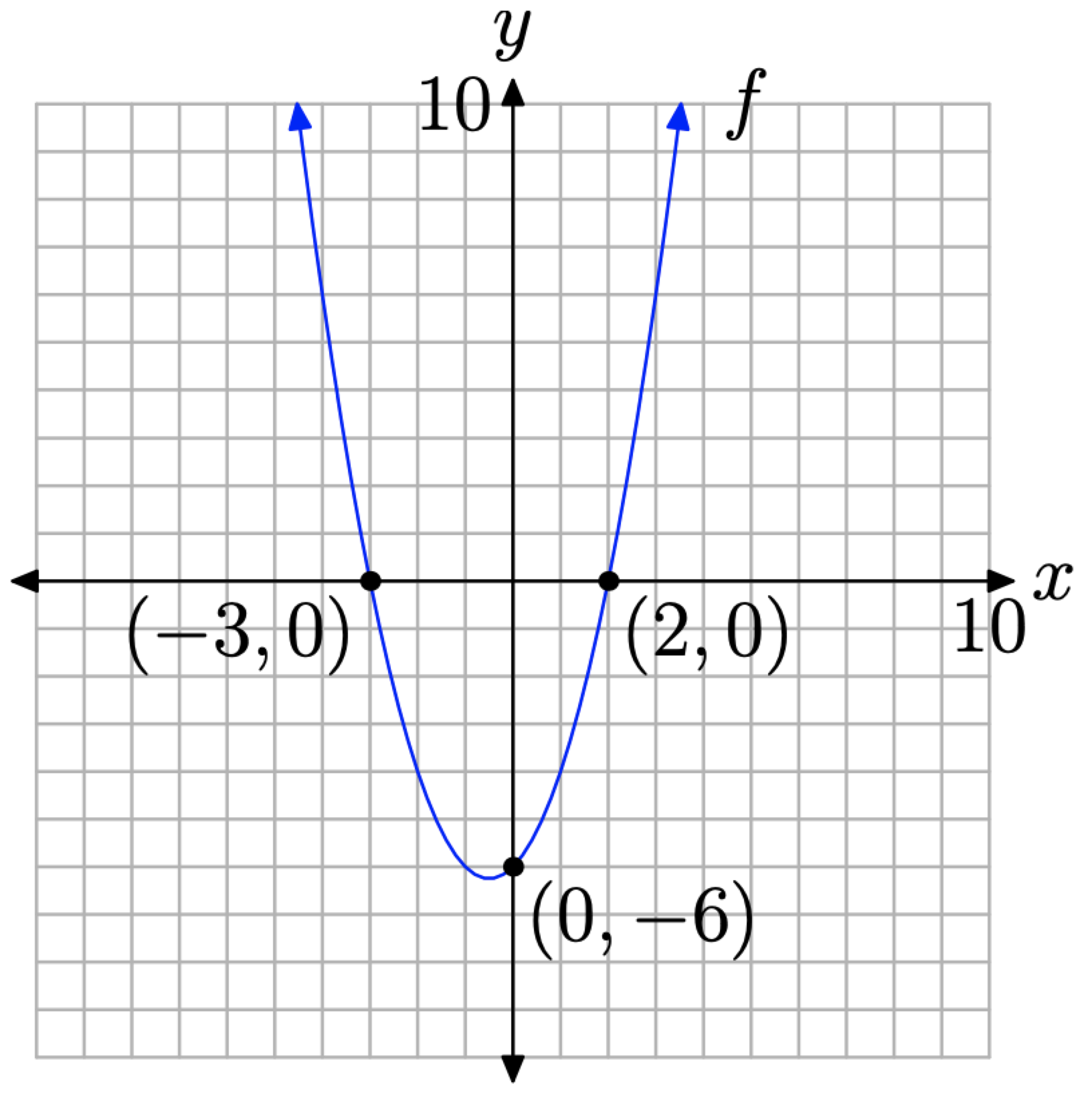
Note that the graph of the f crosses the x-axis at (−3, 0) and (2, 0). These are the x-intercepts of the parabola. Note that the y-coordinate of each x-intercept is zero.

In function notation, the solutions of f(x) = 0 (note the similarity to y = 0) are the x-coordinates of the points where the graph of f crosses the x-axis. Analyzing the graph of f in Figure \(\PageIndex{1}\), we see that both −3 and 2 are solutions of f(x) = 0.

Thus, the process for finding the x-intercepts is clear.

Finding x-intercepts

To find the x-intercepts of the graph of any function, set y = 0 and solve for x. Alternatively, if function notation is used, set f(x) = 0 and solve for x.

Let’s look at an example.

Example \(\PageIndex{5}\)

Find the x-intercepts of the graph of the quadratic function defined by \(y = x^2 + 2x − 48\).

Solution

To find the x-intercepts, first set y = 0.

\[0=x^{2}+2 x-48\]

Next, factor the trinomial on the right. Note that the coefficient of \(x^2\) is 1. We need only think of two integers whose product equals the constant term −48 and whose sum equals the coefficient of x, namely 2. The numbers 8 and −6 come to mind, so the trinomial factors as follows (readers should check this result).

\[0=(x+8)(x-6)\]

To complete the solution, we need to use an important property of the real numbers called the zero product property.

Zero Product Property

If a and b are any real numbers such that \[ab = 0\], then either a = 0 or b = 0.

In our case, we have 0 = (x + 8)(x − 6). Therefore, it must be the case that either

\[x+8=0 \qquad \text { or } \qquad x-6=0\]

These equations can be solved independently to produce

\[x=-8 \quad \text { or } \quad x=6\]

Thus, the x-intercepts of the graph of \(y = x^2 + 2x−48\) are located at (−8, 0) and (6, 0).

Let’s look at another example.

Example \(\PageIndex{6}\)

Find the x-intercepts of the graph of the quadratic function \(f(x) = x^2 − 7x − 18\).

Solution

To find the x-intercepts of the graph of the quadratic function f, we begin by setting

\[f(x)=0\nonumber\]

Of course, \(f(x) = x^2 − 7x − 12\), so we can substitute to obtain

\[x^{2}-7 x-15=0 \nonumber\]

We will now use the c-test to factor the trinomial. Note that c = (−18). List the integer pairs whose products equal −18.

1,-18		1,-18
2,-9		2,-9
3,-6		3,-6

Note that the pair 2,-9 has a sum  of -7 \(x^2 − 7x − 18\). Use this pair to express the middle term as a sum

\[\begin{aligned} x^{2}-7 x-18 &=0 \\  (x+2)(x-9) &=0 \end{aligned}\]

Now we can use the zero product property. Either

\[x-9=0 \qquad \text { or } \qquad  x+2=0 \nonumber\]

Each of these can be solved independently to obtain

\[x=9 \qquad \text { or } \qquad x=-2 \nonumber\]

Thus, the x-intercepts of the graph of the quadratic function \(f(x) = x^2 − 7x − 18\) are located at (9, 0) and (-2, 0).

 

Finding Y-Intercepts

To find the y-intercepts of the graph of any function, set \(x = 0\) and solve for \(y\). Alternatively, if function notation is used, simply evaluate f(0).

Example \(\PageIndex{8}\)

Find the y-intercept of the quadratic function defined by \(f(x) = x^2 − 3x − 11\).

Solution

Evaluate the function at x = 0.

\[f(0)=(0)^{2}-3(0)-11=-11\]

The coordinates of the y-intercept are (0, −11).

Exercises

In Exercises 1-8, factor the given quadratic polynomial.

Exercise \(\PageIndex{1}\)

\(x^2+9x+14\)

Answer

(x+2)(x+7)

Exercise \(\PageIndex{2}\)

\(x^2+6x+5\)

Exercise \(\PageIndex{3}\)

\(x^2+10x+9\)

Answer

(x+9)(x+1)

Exercise \(\PageIndex{4}\)

\(x^2+4x−21\)

Exercise \(\PageIndex{5}\)

\(x^2−4x−5\)

Answer

(x−5)(x+1)

Exercise \(\PageIndex{6}\)

\(x^2+7x−8\)

Exercise \(\PageIndex{7}\)

\(x^2−7x+12\)

Answer

(x−4)(x−3)

Exercise \(\PageIndex{8}\)

\(x^2+5x−24\)

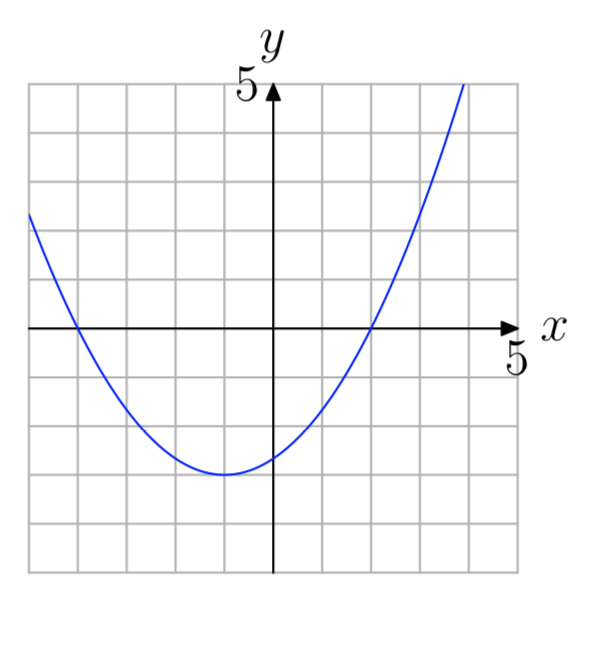
In Exercises 9-14, Use the graph of \(f(x) = ax^2+bx+c\) shown to find all solutions of the equation f(x) = 0. (Note: Every solution is an integer.)

Exercise \(\PageIndex{9}\)

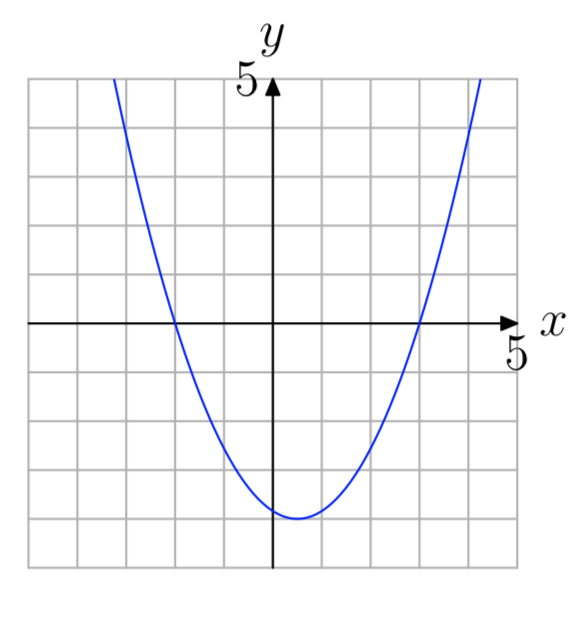
Answer

−2, 3

Exercise \(\PageIndex{10}\)

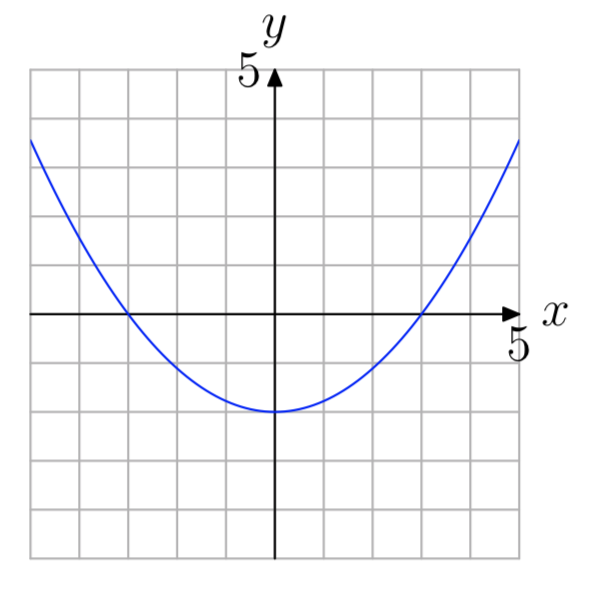
Exercise \(\PageIndex{11}\)

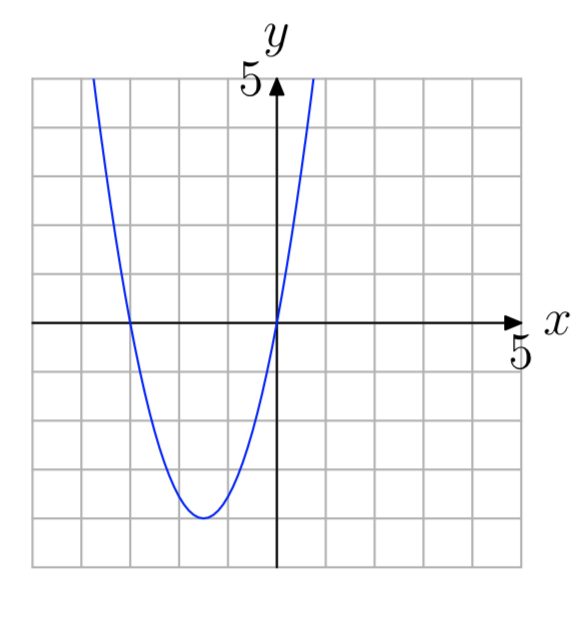
Answer

−3, 0

Exercise \(\PageIndex{12}\)

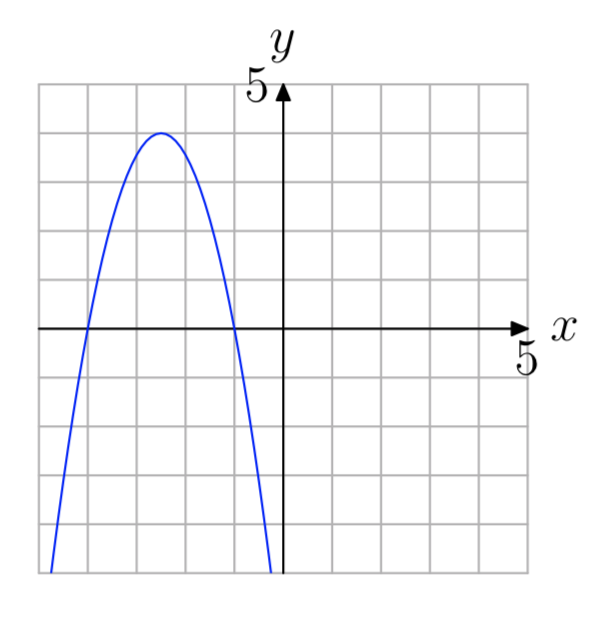
Exercise \(\PageIndex{13}\)

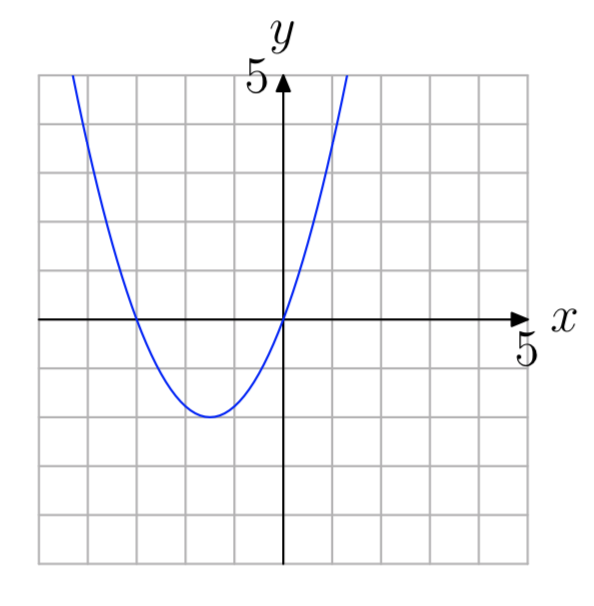
Answer

−3, 0

Exercise \(\PageIndex{14}\)