5.R: Further Applications of Trigonometry (Review)

8.1 & 8.3: Non-right Triangles: Law of Sines

For the exercises 1-5 assume \(\alpha \) is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). Solve each triangle, if possible. Round each answer to the nearest tenth.

1) \(\beta =50^{\circ}, a=105, b=45\)

Answer

Not possible

2) \(\alpha =43.1^{\circ}, a=184.2, b=242.8\)

3) Solve the triangle.

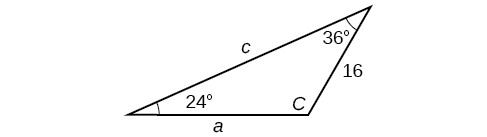
Answer

\(C=120^{\circ}, a=23.1, c=34.1\)

4) Find the area of the triangle.

Figure below. Find the distance of the plane from point \(A\) and the elevation of the plane.

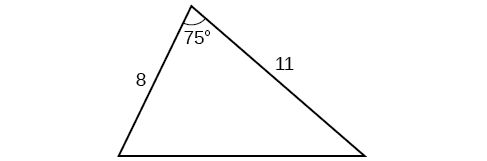
Answer

distance of the plane from point \(A:2.2\) km, elevation of the plane: \(1.6\) km

8.2 & 8.3: Non-right Triangles - Law of Cosines

1) Solve the triangle, rounding to the nearest tenth, assuming \(\alpha \) $$is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) s opposite side \(c: a=4, b=6,c=8\)$\mathrm{.}$

2) Solve the triangle in the Figure below, rounding to the nearest tenth.

Answer

\(B=71.0^{\circ},C=55.0^{\circ},a=12.8\)

3) Find the area of a triangle with sides of length \(8.3\), \(6.6\), and \(9.1\).

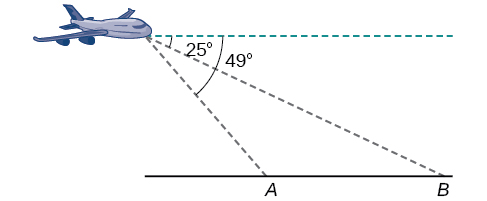
4) To find the distance between two cities, a satellite calculates the distances and angle shown in the Figure below (not to scale). Find the distance between the cities. Round answers to the nearest tenth.

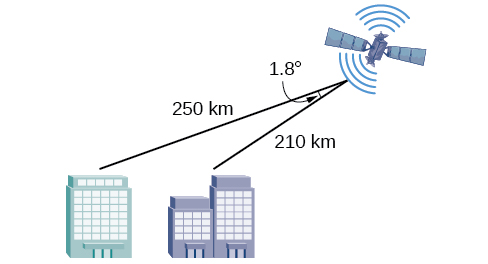
Answer

\(40.6\) km

8.4: Polar Coordinates

1) Plot the point with polar coordinates \(\left ( 3,\dfrac{\pi }{6} \right )\).

2) Plot the point with polar coordinates \(\left ( 5,\dfrac{-2\pi }{3} \right )\).

Answer

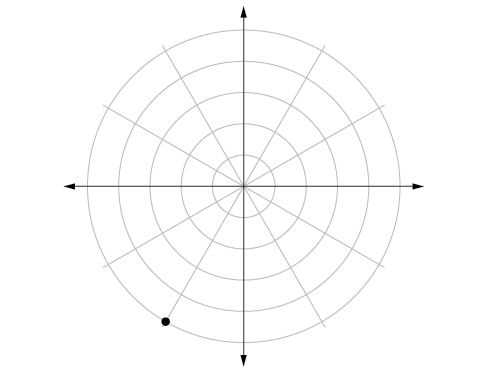
3) Convert \(\left ( 6,\dfrac{-3\pi }{4} \right )\) to rectangular coordinates.

4) Convert \(\left ( -2,\dfrac{3\pi }{2} \right )\) to rectangular coordinates.

Answer

\((0,2)\)

5) Convert \((7,-2)\) to polar coordinates.

6) Convert \((-9,-4)\) to polar coordinates.

Answer

\((9.8489,203.96^{\circ})\)

For the exercises 7-9, convert the given Cartesian equation to a polar equation.

7) \(x=-2\)

8) \(x^2+y^2=64\)

Answer

\(r=8\)

9) \(x^2+y^2=-2y\)

For the exercises 10-11, convert the given polar equation to a Cartesian equation.

10) \(r=7\cos \theta\)

Answer

\(x^2+y^2=7x\)

11) \(r=\dfrac{-2}{4\cos \theta +\sin \theta }\)

For the exercises 12-13, convert to rectangular form and graph.

12) \(\theta =\dfrac{3\pi }{4}\)

Answer

\(y=-x\)

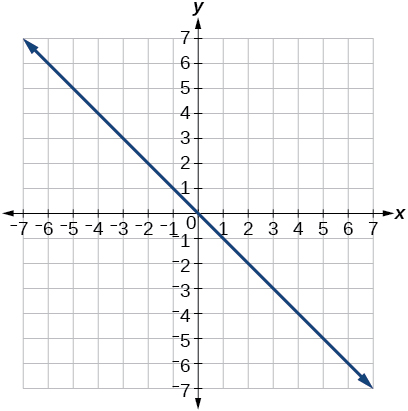
13) \(r=5\sec \theta\)

8.5: Polar Coordinates - Graphs

For the exercises 1-5, test each equation for symmetry.

1) \(r=4+4\sin \theta\)

Answer

symmetric with respect to the line \(\theta =\dfrac{\pi }{2}\)

2) \(r=7\)

3) Sketch a graph of the polar equation \(r=1-5\sin \theta\). Label the axis intercepts.

Answer

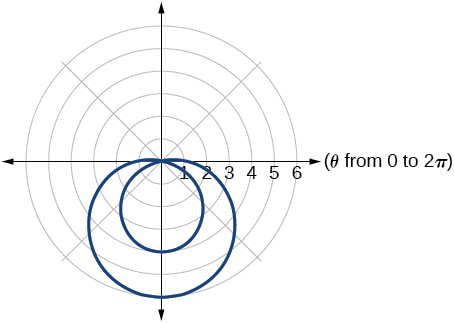
4) Sketch a graph of the polar equation \(r=5\sin (7\theta )\).

5) Sketch a graph of the polar equation \(r=3-3\cos \theta\)

Answer

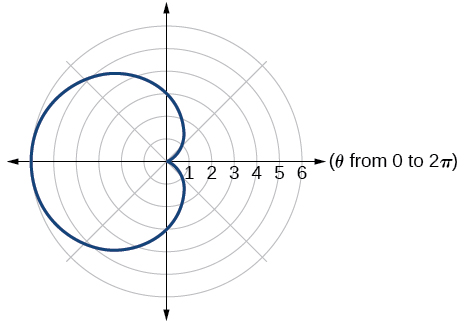
8.6: Polar Form of Complex Numbers

For the exercises 1-2, find the absolute value of each complex number.

1) \(-2+6i\)

2) \(4-3i\)

Answer

\(5\)

Write the complex number in polar form.

3) \(5+9i\)

4) \(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i\)

Answer

\(\mathrm{cis}\left (-\dfrac{\pi }{3} \right )\)

For the exercises 5-6, convert the complex number from polar to rectangular form.

5) \(z=5\mathrm{cis}\left (\dfrac{5\pi }{6} \right )\)

6) \(z=3\mathrm{cis}(40^{\circ})\)

Answer

\(2.3+1.9i\)

For the exercises 7-8, find the product \(z_1 z_2\) in polar form.

7) \(\begin{align*} z_1 &= 2\mathrm{cis}(89^{\circ})\\ z_2 &= 5\mathrm{cis}(23^{\circ}) \end{align*}\)

8) \(\begin{align*} z_1 &= 10\mathrm{cis}\left ( \dfrac{\pi }{6} \right )\\ z_2 &= 6\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}\)

Answer

\(60\mathrm{cis}\left ( \dfrac{\pi }{2} \right )\)

For the exercises 9-10, find the quotient \(\dfrac{z_1}{z_2}\) in polar form.

9) \(\begin{align*} z_1 &= 12\mathrm{cis}(55^{\circ})\\ z_2 &= 3\mathrm{cis}(18^{\circ}) \end{align*}\)

10) \(\begin{align*} z_1 &= 27\mathrm{cis}\left ( \dfrac{5\pi }{3} \right )\\ z_2 &= 9\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}\)

Answer

\(3\mathrm{cis}\left ( \dfrac{4\pi }{3} \right )\)

For the exercises 11-12, find the powers of each complex number in polar form.

11) Find \(z^4\) when \(z=2\mathrm{cis}(70^{\circ})\)

12) Find \(z^2\) when \(z=5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )\)

Answer

\(25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )\)

For the exercises 13-14, evaluate each root.

13) Evaluate the cube root of \(z\) when \(z=64\mathrm{cis}(210^{\circ})\).

14) Evaluate the square root of \(z\) when \(z=25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )\).

Answer

\(5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )\), \(5\mathrm{cis}\left ( \dfrac{7\pi }{4} \right )\)

For the exercises 15-16, plot the complex number in the complex plane.

15) \(6-2i\)

16) \(-1+3i\)

Answer

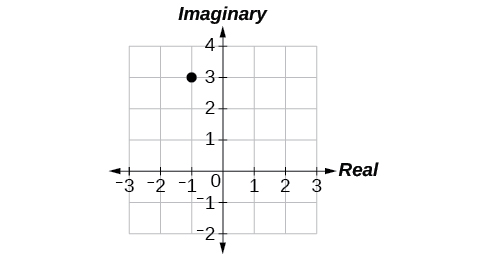
8.7: Parametric Equations

1) \(\begin{cases} & x(t)= 3t-1\\ & y(t)= \sqrt{t} \end{cases}\)

2) \(\begin{cases} & x(t)= -\cos t\\ & y(t)= 2\sin ^2t \end{cases}\)

Answer

\(x^2+\dfrac{1}{2}y=1\)

3) Parameterize (write a parametric equation for) each Cartesian equation by using \(x(t)=a\cos t\) and \(y(t)=b\sin t\) for \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\).

4) Parameterize the line from \((-2,3)\) to \((4,7)\) so that the line is at \((-2,3)\) at \(t=0\) and \((4,7)\) at \(t=1\).

Answer

\(\begin{cases} & x(t)= -2+6t\\ & y(t)= 3+4t \end{cases}\)

8.8: Parametric Equations - Graphs

For the exercises 1-, make a table of values for each set of parametric equations, graph the equations, and include an orientation; then write the Cartesian equation.

1) \(\begin{cases} & x(t)= 3t^2\\ & y(t)= 2t-1 \end{cases}\)

2) \(\begin{cases} & x(t)= e^t\\ & y(t)= -2e^{5t} \end{cases}\)

Answer

\(y=-2x^5\)

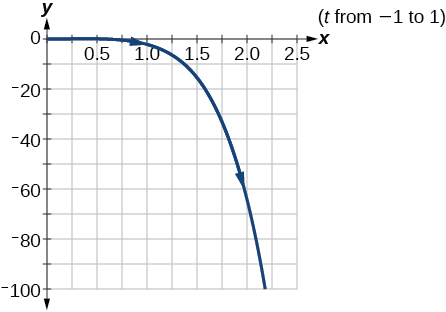
3) \(\begin{cases} & x(t)= 3\cos t\\ & y(t)= 2\sin t \end{cases}\)

4) A ball is launched with an initial velocity of \(80\) feet per second at an angle of \(40^{\circ}\) to the horizontal. The ball is released at a height of \(4\) feet above the ground.

1. Where is the ball after \(3\) seconds?
2. How long is the ball in the air?

Answer

1. \(\begin{cases} & x(t)= (80\cos (40^{\circ}))t\\ & y(t)= -16t^2+(80\sin (40^{\circ}))t+4 \end{cases}\)
2. The ball is 14 feet high and 184 feet from where it was launched.
3. \(3.3\) seconds

 

Practice Test

1) Assume \(\alpha \) is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). Solve the triangle, if possible, and round each answer to the nearest tenth, given \(\beta =68^{\circ},b=21,c=16\).

Answer

\(\alpha =67.1^{\circ}, \gamma =44.9^{\circ}, a=20.9\)

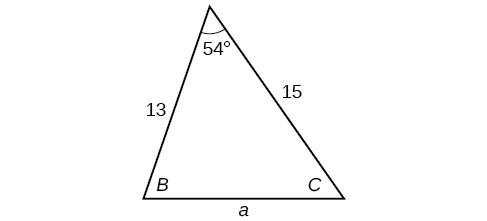
2) Find the area of the triangle in the Figure below (from chapter 8). Round each answer to the nearest tenth.

 

 

 

 

 

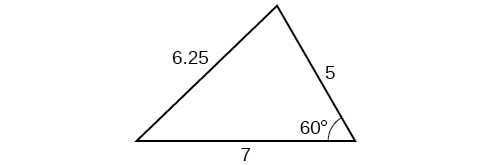
3) A pilot flies in a straight path for \(2\) hours. He then makes a course correction, heading \(15^{\circ}\) to the right of his original course, and flies \(1\) hour in the new direction. If he maintains a constant speed of \(575\) miles per hour, how far is he from his starting position?

Answer

\(1712\) miles

4) Convert \((2,2)\) to polar coordinates, and then plot the point.

 

5) Convert \(\left ( 2,\dfrac{\pi }{3} \right )\) to rectangular coordinates.

Answer

\((1,\sqrt{3})\)

 

6) Convert the polar equation to a Cartesian equation: \(x^2+y^2=5y\).

7) Convert to rectangular form and graph:\(r=-3\csc θ\).

Answer

\(y=-3\)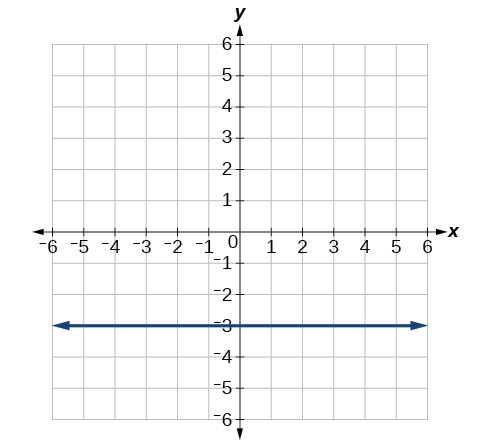

8) Test the equation for symmetry: \(r=-4\sin(2\theta )\).

 

9) Graph \(r=3+3\cos \theta\).

Answer

 

10) Graph \(r=3-5\sin \theta\).

 

11) Find the absolute value of the complex number \(5-9i\).

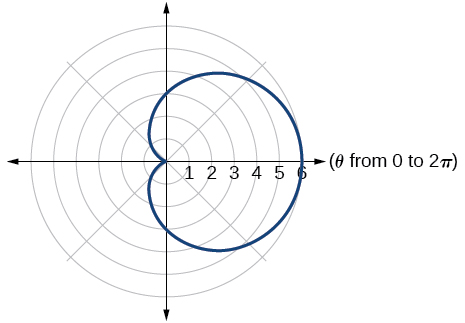
Answer

\(\sqrt{106}\)

12) Write the complex number in polar form: \(4+i\).

13) Convert the complex number from polar to rectangular form: \(z=5\mathrm{cis}\left ( \dfrac{2\pi }{3} \right )\)

Answer

\(\dfrac{-5}{2}+i\dfrac{5\sqrt{3}}{2}\)

14) \(z_1 z_2\)

15) \(\dfrac{z_1}{z_2}\)

Answer

\(4\mathrm{cis}(21^{\circ})\)

16) \((z_2)^3\)

17) \(\sqrt{z_1}\)

Answer

\(2\sqrt{2}\mathrm{cis}(18^{\circ}), 2\sqrt{2}\mathrm{cis}(198^{\circ})\)

18) Plot the complex number \(-5-i\) in the complex plane.

19) Eliminate the parameter \(t\) to rewrite the following parametric equations as a Cartesian equation: \(\begin{cases} & x(t)= t+1\\ & y(t)= 2t^2 \end{cases}\)

Answer

\(y=2(x-1)^2\)

20) Parameterize (write a parametric equation for) the following Cartesian equation by using \(x(t)=a\cos t\) and \(y(t)=b\sin t : \dfrac{x^2}{36}+\dfrac{y^2}{100}=1\)

21) Graph the set of parametric equations and find the Cartesian equation: \(\begin{cases} & x(t)= -2\sin t\\ & y(t)= 5\cos t \end{cases}\)

Answer

 

22) A ball is launched with an initial velocity of \(95\) feet per second at an angle of \(52^{\circ}\) to the horizontal. The ball is released at a height of \(3.5\) feet above the ground.

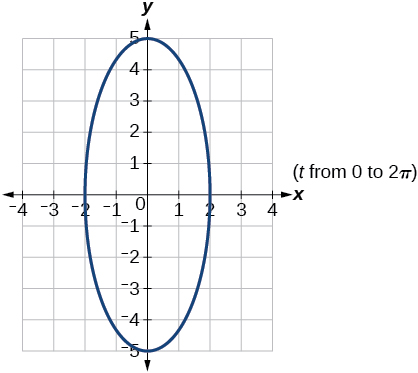
1. Where is the ball after \(2\) seconds?
2. How long is the ball in the air?

 

Contributors and Attributions

 

 

 

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

 

 

 

 

 

 

 

 

 

 

 

 

 

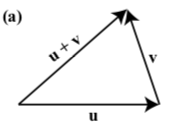
In each of the following diagrams, one of the vectors \(\textbf{u}\), \(\textbf{v}\), and \(\textbf{u} + \textbf{v}\) is labeled.

NOTE: In each diagram \(\textbf{u}\), \(\textbf{v}\), and \(\textbf{u} + \textbf{v}\) may represent different vectors.

TASK: Label the other two vectors to make the diagram a valid representation of \(\textbf{u} + \textbf{v}\)

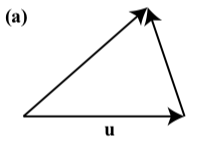
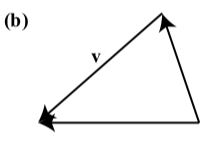
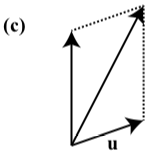
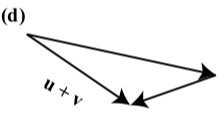
Answer

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

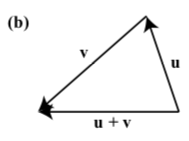
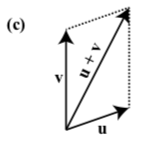
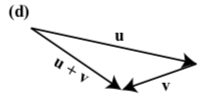
Exercise \(\PageIndex{2}\)

On the following diagram, draw the vectors \(\textbf{u} + \textbf{v}\), \(\textbf{u} - \textbf{v}\), \(2\textbf{u} + \textbf{v}\), and \(2\textbf{u} - \textbf{v}\).

Figure \(\PageIndex{11}\)

Answer

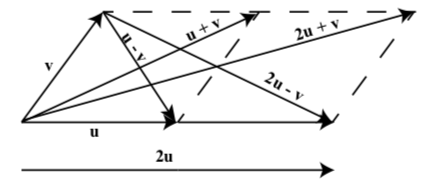
Figure \(\PageIndex{12}\)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{3}\)

In the following diagram, \(|\textbf{a}| = 10\) and \(|\textbf{a}| + |\textbf{b}| = 14\). In addition, the angle \(\theta\) between the vectors \(\textbf{a}\) and \(\textbf{b}\) is \(30^\circ\). Determine the magnitude of the vector \(\textbf{b}\) and the angle between the vectors \(\textbf{a}\) and \(\textbf{a} + \textbf{b}\).

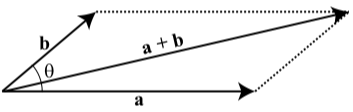
Figure \(\PageIndex{13}\)

Answer

The angle between the vectors \(\textbf{a}\) and \(\textbf{a} + \textbf{b}\) is approximately \(9.075^\circ\). In addition, \(|\textbf{b}| \approx 4.416\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{4}\)

Suppose that vectors \(\textbf{a}\) and \(\textbf{b}\) have magnitudes of 125 and 180, respectively. Also assume that the angle between these two vectors is \(35^\circ\). Determine the magnitude of the vector \(\textbf{a} + \textbf{b}\) and the measure of the angle between the vectors \(\textbf{a}\) and \(\textbf{a} + \textbf{b}\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{5}\)

A car that weighs \(3250\) pounds is on an inclined plane that makes an angle of \(4.5^\circ\) with the horizontal. Determine the magnitude of the force of the car on the inclined plane, and determine the magnitude of the force on the car down the plane due to gravity. What is the magnitude of the smallest force necessary to keep the car from rolling down the plane?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{6}\)

An experiment determined that a force of \(45\) pounds is necessary to keep a \(250\) pound object from sliding down an inclined plane. Determine the angle the inclined plane makes with the horizontal.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{7}\)

A cable that can withstand a force of \(4500\) pounds is used to pull an object up an inclined plane that makes an angle of 15 degrees with the horizontal. What is the heaviest object that can be pulled up this plane with the cable? (Assume that friction can be ignored.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{8}\)

Determine the magnitude and the direction angle of each of the following vectors.

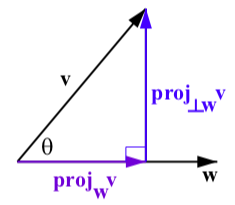
Figure \(\PageIndex{14}\): The Projection of \(\textbf{v}\) onto \(\textbf{w}\)

1. \[\textbf{v} = 3\textbf{i} + 5\textbf{j}\]
2. \[\textbf{w} = \langle -3, 6 \rangle\]
3. \[\textbf{a} = 4\textbf{i} - 7\textbf{j}\]
4. \[\textbf{u} = \langle -3, -5 \rangle\]

Answer

1. \(|\textbf{v}| = \sqrt{34}\). The direction angle is approximately \(59.036^\circ\).
2. \(|\textbf{w}| = \sqrt{45}\). The direction angle is approximately \(116.565^\circ\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{9}\)

Determine the horizontal and vertical components of each of the following vectors. Write each vector in \(\textbf{i}\), \(\textbf{j}\) form.

The vector \(\textbf{v}\) with magnitude 12 and direction angle \(50^\circ\)?

The vector \(\textbf{u}\) with \(\textbf{u} = \sqrt{20}\) and direction angle \(125^\circ\).

The vector \(\textbf{w}\) with magnitude \(5.25\) and direction angle \(200^\circ\).

Answer

1. \(\textbf{v} = 12\cos(50^\circ) + 12\sin(50^\circ) \approx 7.713\textbf{i} + 9.193\textbf{j}\).
2. \(\textbf{u} = \sqrt{20}\cos(125^\circ) + \sqrt{20}\sin(125^\circ) \approx -2.565\textbf{i} + 3.663\textbf{j}\)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{10}\)

Let \(\textbf{u} = 2\textbf{i} + 3\textbf{j}\), \(\textbf{v} = -\textbf{i} + 5\textbf{j}\), and \(\textbf{w} = 4\textbf{i} - 2\textbf{j}\). Determine the \(\textbf{i}\), \(\textbf{j}\) form of each of the following:

1. \[5\textbf{u} - \textbf{v}\]
2. \[2\textbf{v} + 7\textbf{w}\]
3. \[\textbf{u} + \textbf{v} + \textbf{w}\]
4. \[3\textbf{u} + 5\textbf{w}\]

Answer

1. \(5\textbf{u} - \textbf{v} = 11\textbf{i} + 10\textbf{j}\)

3. \(\textbf{u} + \textbf{v} + \textbf{w} = 5\textbf{i} + 6\textbf{j}\)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{11}\)

Determine the value of the dot product for each of the following pairs of vectors.

1. \(\textbf{v} = 2\textbf{i} + 5\textbf{j}\) and \(\textbf{w} = 3\textbf{i} - 2\textbf{j}\)
2. \(\textbf{a}\) and \(\textbf{b}\) where \(|\textbf{a}| = 6\), \(|\textbf{w}| = 3\), and the angle between \(\textbf{v}\) and \(\textbf{w}\) is \(30^\circ\)
3. \(\textbf{a}\) and \(\textbf{b}\) where \(|\textbf{a}| = 6\), \(|\textbf{w}| = 3\), and the angle between \(\textbf{v}\) and \(\textbf{w}\) is \(150^\circ\)
4. \(\textbf{a}\) and \(\textbf{b}\) where \(|\textbf{a}| = 6\), \(|\textbf{w}| = 3\), and the angle between \(\textbf{v}\) and \(\textbf{w}\) is \(50^\circ\)
5. \(\textbf{a} = 5\textbf{i} - 2\textbf{j}\) and \(\textbf{b} = 2\textbf{i} + 5\textbf{j}\)

Answer

1. \(\textbf{v}\cdot\textbf{w} = -4\).

2. \(\textbf{a}\cdot\textbf{b} = 9\sqrt{3}\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{12}\)

Determine the angle between each of the following pairs of vectors.

1. \[\textbf{v} = 2\textbf{i} + 5\textbf{j}\] and \[\textbf{w} = 3\textbf{i} - 2\textbf{j}\]
2. \[\textbf{a} = 5\textbf{i} - 2\textbf{j}\] and \[\textbf{b} = 2\textbf{i} + 5\textbf{j}\]
3. \[\textbf{v} = 3\textbf{i} - 2\textbf{j}\] and \[\textbf{w} = -\textbf{i} + 4\textbf{j}\]

Answer

1. The angle between \(\textbf{v}\) and \(\textbf{w}\) is \(\cos^{-1}(\dfrac{-4}{\sqrt{29}\sqrt{13}}) \approx 101.89^\circ\).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercise \(\PageIndex{13}\)

For each pair of vectors, determine \(\textbf{proj}_{\textbf{v}}\textbf{w}\), \(\textbf{proj}_{\perp\textbf{v}}\textbf{w}\) and verify that

\(\textbf{w} = \textbf{proj}_{\perp\textbf{w}}\textbf{v} + \textbf{proj}_{\textbf{w}}\textbf{v}\). Draw a picture showing all of the vectors involved in this.

1. \[\textbf{v} = 2\textbf{i} + 5\textbf{j}\] and \[\textbf{w} = 3\textbf{i} - 2\textbf{j}\]
2. \[\textbf{v} = \langle -2, 3 \rangle\] and \[\textbf{w} = \langle 1, 1 \rangle\]

Answer

1. \[\textbf{proj}_{v}\textbf{w} = \dfrac{\textbf{w}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v} = \dfrac{-4}{29}(2\textbf{i} + 5\textbf{j}) = -\dfrac{8}{29}\textbf{i} - \dfrac{20}{29}\textbf{j}\]

\[\textbf{proj}_{\perp_\textbf{v}}\textbf{w} = \textbf{w} - \textbf{proj}_{v}\textbf{w} = \dfrac{95}{29}\textbf{i} - \dfrac{38}{29}\textbf{j}\]

 

 

 

 

 

 

 

Contributor

 

 

 

 

 

 

 

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.