1.3: Introduction to the Integers
- Last updated
- Save as PDF
- Page ID
- 30965
As we saw in the introduction to the chapter, negative numbers have a rich and storied history. One of the earliest applications of negative numbers had to do with credits and debits. For example, if $5 represents a credit or profit, then −$5 represents a debit or loss. Of course, the ancients had a different monetary system than ours, but you get the idea. Note that if a vendor experiences a profit of $5 on a sale, then a loss of −$5 on a second sale, the vendor breaks even. That is, the sum of $5 and −$5 is zero. In much the same way, every whole number has an opposite or negative counterpart.
The Opposite or Negative of a Whole Number
For every whole number a, there is a unique number −a, called the opposite or negative of a, such that a + (−a) = 0.
The opposite or negative of any whole number is easily located on the number line.
Number Line Locations
To locate the opposite (or negative) of any whole number, first locate the whole number on the number line. The opposite is the reflection of the whole number through the origin (zero).
Example 1
Locate the whole number 5 and its opposite (negative) on the number line.
Solution
Draw a number line, then plot the whole number 5 on the line as a shaded dot.
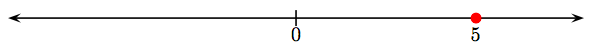
To find its opposite, reflect the number 5 through the origin. This will be the location of the opposite (negative) of the whole number 5, which we indicate by the symbol −5.
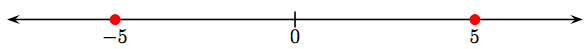
Note the symmetry. The whole number 5 is located five units to the right of zero. Its negative is located five units to the left of zero.
Exercise
Locate the number -7 and its opposite on the number line.
Important Pronunciation
The symbol −5 is pronounced in one of two ways: (1) “negative five,” or (2) “the opposite of five.”
In similar fashion, we can locate the opposite or negative of any whole number by reflecting the whole number through the origin (zero), which leads to the image shown in Figure 2.1.
The Integers
The collection of numbers arranged on the number line in Figure 2.1 extend indefinitely to the right, and because the numbers on the left are reflections through the origin, the numbers also extend indefinitely to the left. This collection of numbers is called the set of integers.
The Integers
The infinite collection of numbers
{..., −7, −6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6, 7, ...}
is called the set of integers.
The ellipsis . . . at each end of this infinite collection means “etcetera,” as the integers continue indefinitely to the right and left. Thus, for example, both 23,456 and −117, 191 are elements of this set and are therefore integers.
Ordering the Integers
As we saw with the whole numbers, as you move to the right on the number line, the numbers get larger; as you move to the left, the numbers get smaller.
Order on the Number Line
Let a and b be integers located on the number line so that the point representing the integer a lies to the left of the point representing the integer b.

Then the integer a is “less than” the integer b and we write
\[ a < b\nonumber \]
Alternatively, we can also say that the integer b is “larger than” the integer a and write
\[ b > a.\nonumber \]
Example 3
Replace each shaded box with < (less than) or > (greater than) so the resulting inequality is a true statement.

Solution
For the first case, locate −3 and 5 on the number line as shaded dots.
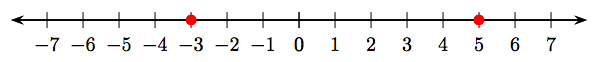
Note that −3 lies to the left of 5, so:
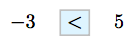
That is, −3 is “less than” 5.
In the second case, locate −2 and −4 as shaded dots on the number line.
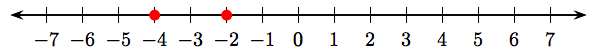
Note that −2 lies to the right of −4, so:

That is, −2 is “greater than” −4.
Exercise
Compare −12 and −11.
- Answer
-
−12 < −11
Important Observation
In Example 3, note that the “pointy end” of the inequality symbol always points towards the smaller number.
We stated earlier that every integer has a unique number called its “opposite” or “negative.” Thus, the integer −5 is the opposite (negative) of the integer 5. Thus, we can say that the pair −5 and 5 are opposites. Each is the opposite of the other. Logically, this leads us to the conclusion that the opposite of −5 is 5. In symbols, we would write
\[ -(-5) = 5.\nonumber \]
Opposites of Opposites
Let a be an integer. Then the “opposite of the opposite of a is a.” In symbols, we write
\[ -(-a) = a.\nonumber \]
We can also state that the “negative of a negative a is a.
Example 4
Simplify −(−13) and −(−119).
Solution
The opposite of the opposite of a number returns the original number. That is,
−(−13) = 13 and − (−119) = 11.
Exercise
Simplify: −(−50).
- Answer
-
50
Positive and Negative
We now define the terms positive integer and negative integer.
Positive Integer
If a is an integer that lies to the right of zero (the origin) on the number line, then a is a positive integer. This means that a is a positive integer if and only if a > 0.
Thus, 2, 5, and 117 are positive integers.
Negative Integer
If a is an integer that lies to the left of zero (the origin) on the number line, then a is a negative integer. This means that a is a negative integer if and only if a < 0.
Thus, −4, −8, and −1, 123 are negative integers.
Zero
The integer zero is neither positive nor negative.
Example 5
Classify each of the following numbers as negative, positive, or neither: 4, −6, and 0.
Solution
Locate 4, −6, and 0 on the number line.

Thus:
- 4 lies to the right of zero. That is, 4 > 0, making 4 a positive integer.
- −6 lies to the left of zero. That is, −6 < 0, making −6 a negative integer.
- The number 0 is neutral. It is neither negative nor positive.
Exercise
Classify −11 as positive, negative, or neither.
- Answer
-
Negative
Absolute Value
We define the absolute value of an integer.
Absolute Value
The absolute value of an integer is defined as its distance from the origin (zero).
It is important to note that distance is always a nonnegative quantity (not negative); i.e., distance is either positive or zero. As an example, we’ve shaded the integers −4 and 4 on a number line.
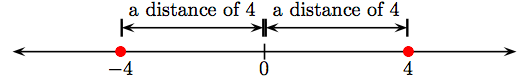
The number line above shows two cases:
- The integer −4 is 4 units from zero. Because absolute value measures the distance from zero, | − 4| = 4.
- The integer 4 is also 4 units from zero. Again, absolute value measures the distance from zero, so |4| = 4.
Let’s look at another example.
Example 6
Determine the value of each expression: a) | − 7|, b) |3|, and c) |0|.
Solution
The absolute value of any integer is equal to the distance that number is from the origin (zero) on the number line. Thus:
a) The integer −7 is 7 units from the origin; hence, | − 7| = 7.
b) The integer 3 is 3 units from the origin; hence, |3| = 3.
c) The integer 0 is 0 units from the origin; hence, |0| =0.
Exercise
Simplify: | − 33|.
- Answer
-
33
Example 7
Determine the value of each expression: a) −(−8) and b) −| − 8|
Solution
These are distinctly different problems.
a) The opposite of −8 is 8. That is, −(−8) = 8.
b) However, in this case, we take the absolute value of −8 first, which is 8, then the opposite of that result to get −8. That is,
\[ \begin{aligned} - | -8 | = -(8) & \textcolor{red}{ \text{ First: } |-8| = 8.} \\ = -8 ~ & \textcolor{red}{ \text{ Second: The opposite of 8 is } -8.} \end{aligned}\nonumber \]
Exercise
Simplify: −| − 50|.
- Answer
-
50
Applications
There are a number of applications that benefit from the use of integers.
Example 8
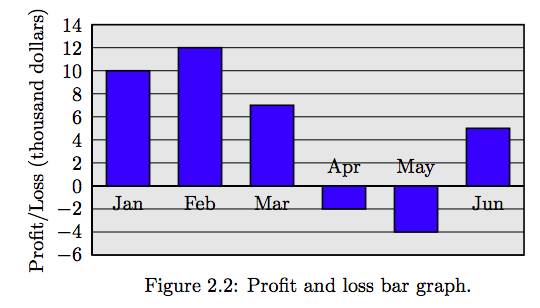
Profits and losses for the first six months of the fiscal year for a small business are shown in Table 2.1. Profits and losses are measured in thousands of dollars. A positive number represents a profit, while a negative number represents a loss. Create a bar graph representing the profits and losses for this small business for each month of the first half of the fiscal year.
| Month | Jan | Feb | Mar | Apr | May | Jun |
| Profit/Loss | 10 | 12 | 7 | -2 | -4 | 5 |
Table 2.1: Profit and loss are measured in thousands of dollars.
Solution
Start by labeling the horizontal axis with the months of the fiscal year. Once you’ve completed that task, scale the vertical axis to accommodate the Profit/Loss values recorded in Table 2.1. Finally, starting at the 0 level on the horizontal axis, sketch bars having heights equal to the profit and loss for each month.
Exercise
The following table contains record low temperatures (degrees Fahrenheit) for Jackson Hole, Wyoming for the indicated months.
| Month | Temp |
| Sept. | 14 |
| Oct. | 2 |
| Nov. | −27 |
| Dec. | −49 |
| Jan. | −50 |
Create a bar graphs of temperature versus months.
Example 9
Table 2.2 contains the low temperature recordings (degrees Fahrenheit) on five consecutive days in Fairbanks, Alaska, 1995. Create a line graph for the data in Table 2.2.
| Date | Jan 21 | Jan 22 | Jan 23 | Jan 24 | Jan 25 |
| Low Temp | 1 | 10 | 5 | −20 | −28 |
Solution
Start by labeling the horizontal axis with the days in January that the temperatures occurred. Scale the vertical axis to accommodate the temperatures given in Table 2.2. Finally, plot points on each day at a height that equals the temperature for that given day. Connect consecutive pairs of points with line segments to produce the line graph shown in Figure 2.3.
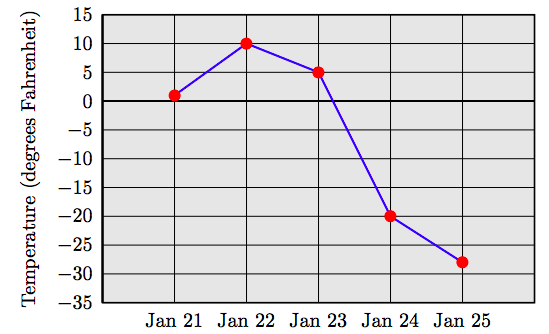
Note that the points in Figure 2.3 have heights greater than zero for January 21-23, representing temperatures greater than zero. The points representing January 24-45 have negative heights corresponding to the negative temperatures of Table 2.2.
Exercise
A man stands on the roof of a multistory building and throws a baseball vertically upward. The height (in feet) of the ball above the edge of the roof at measured times (in seconds) is given in the following table.
| Time | Height |
| 0 | 0 |
| 1 | 24 |
| 2 | 16 |
| 3 | −24 |
| 4 | −96 |
Create a line graph of the height of the ball versus time in the air.
Exercises
In Exercises 1-12, for each of the following questions, provide a number line sketch with your answer.
1. What number lies three units to the left of 4 on the number line?
2. What number lies three units to the left of 1 on the number line?
3. What number lies three units to the left of 6 on the number line?
4. What number lies four units to the left of −2 on the number line?
5. What number lies two units to the right of 0 on the number line?
6. What number lies four units to the right of −2 on the number line?
7. What number lies two units to the right of 1 on the number line?
8. What number lies two units to the right of −4 on the number line?
9. What number lies four units to the left of 6 on the number line?
10. What number lies two units to the left of 0 on the number line?
11. What number lies two units to the right of −5 on the number line?
12. What number lies three units to the right of −6 on the number line?
In Exercises 13-24, for each of the following sets of integers, perform the following tasks:
- Plot each of the integers on a numberline.
- List the numbers in order, from smallest to largest.
13. 6, 1, −3, and −5
14. 5, −3, −5, and 2
15. 5, −6, 0, and 2
16. 4, 2, 6, and −4
17. −3, −5, 3, and 5
18. −4, 5, 2, and −6
19. −5, 4, 2, and −3
20. 6, 1, −3, and −1
21. 3, 5, −5, and −1
22. −4, 6, −2, and 3
23. −2, −4, 3, and −6
24. 2, −6, −4, and 5
In Exercises 25-36, in each of the following exercises, enter the inequality symbol < or the symbol > in the box in order that the resulting inequality is a true statement.
25. \( -4 \square 0\)
26. \(-4 \square 3\)
27. \(-2 \square -1\)
28. \(3 \square 0\)
29. \(-3 \square -1\)
30. \(6 \square 5\)
31. \(3 \square 6\)
32. \(-4 \square -2\)
33. \(-3 \square -6\)
34. \(0 \square -3\)
35. \(-1 \square 4\)
36. \(1 \square -4\)
In Exercises 37-52, simplify each of the following expressions.
37. −(−4).
38. −(−6).
39. |7|.
40. |1|.
41. |5|.
42. |3|.
43. −| − 11|.
44. −| − 1|.
45. | − 5|.
46. | − 1|.
47. −| − 20|.
48. −| − 8|.
49. | − 4|.
50. | − 3|.
51. −(−2).
52. −(−17).
In Exercises 53-64, for each of the following exercises, provide a number line sketch with your answer.
53. Find two integers on the number line that are 2 units away from the integer 2.
54. Find two integers on the number line that are 2 units away from the integer −3.
55. Find two integers on the number line that are 4 units away from the integer −3.
56. Find two integers on the number line that are 2 units away from the integer −2.
57. Find two integers on the number line that are 3 units away from the integer −2.
58. Find two integers on the number line that are 4 units away from the integer 1.
59. Find two integers on the number line that are 2 units away from the integer 3.
60. Find two integers on the number line that are 3 units away from the integer 3.
61. Find two integers on the number line that are 3 units away from the integer 0.
62. Find two integers on the number line that are 4 units away from the integer 2.
63. Find two integers on the number line that are 2 units away from the integer 0.
64. Find two integers on the number line that are 3 units away from the integer 1.
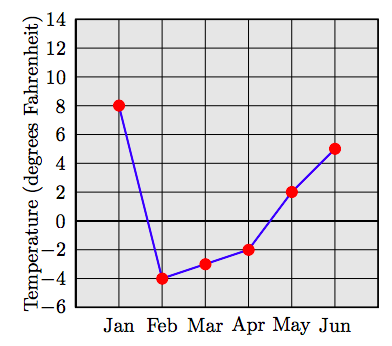
65. Dam. Utah’s lowest point of elevation is 2,350 feet above sea level and occurs at Beaver Dam Wash. Express the height as an integer. 66. Underwater Glider. The National Oceanic and Atmospheric Administration’s underwater glider samples the bottom of the Atlantic Ocean at 660 feet below sea level. Express that depth as an integer. Associated Press Times-Standard 4/19/09 67. Profits and losses for the first six months of the fiscal year for a small business are shown in the following bar chart.
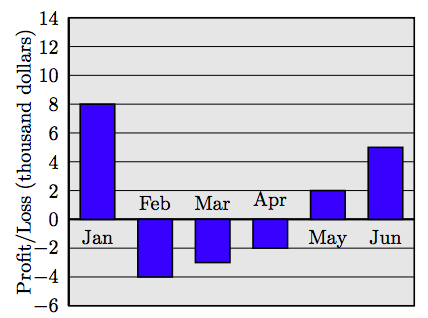
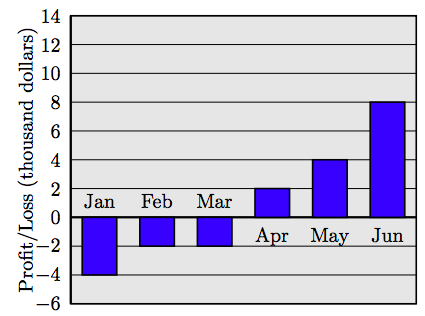
Create a table showing the profit and loss for each month. Use positive integers for the profit and negative integers for the loss. Create a line graph using the data in your table. 68. Profits and losses for the first six months of the fiscal year for a small business are shown in the following bar chart.
Create a table showing the profit and loss for each month. Use positive integers for the profit and negative integers for the loss. Create a line graph using the data in your table. 69. The following line graph displays the low temperature recordings (degrees Fahrenheit) on five consecutive days in Big Bear, California. What was the lowest temperature reading for the week and on what date did it occur?
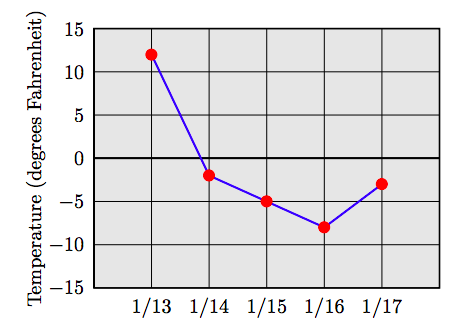
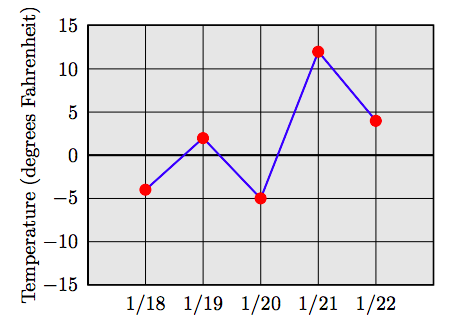
70. The following line graph displays the low temperature recordings (degrees Fahrenheit) on five consecutive days in Ogden, Utah. What was the lowest temperature reading for the week and on what date did it occur?
71. The following table contains the low temperature recordings (degrees Fahrenheit) on five consecutive days in Littletown, Ohio. Create a line graph for the data.
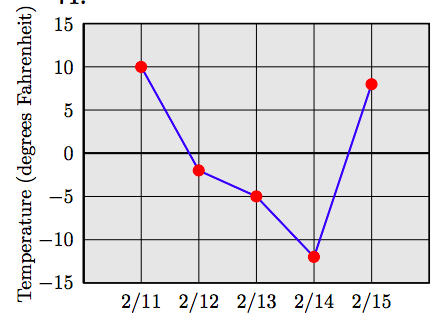
| Date | Feb 11 | Feb 12 | Feb 13 | Feb 14 | Feb 15 |
| Low Temp | 10 | -2 | -5 | -12 | 8 |
72. The following table contains the low temperature recordings (degrees Fahrenheit) on five consecutive days in MyTown, Ottawa. Create a line graph for the data.
| Date | Apr 20 | Apr 21 | Apr 22 | Apr 23 | Apr 24 |
| Low Temp | -10 | -2 | 8 | 5 | -5 |
Answers
1.
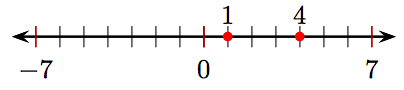
3.
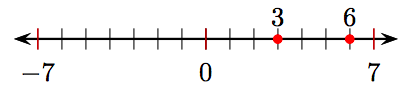
5.
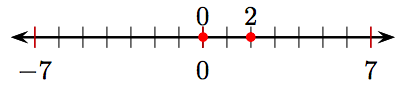
7.
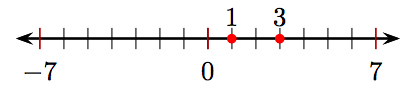
9.
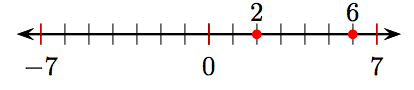
11.
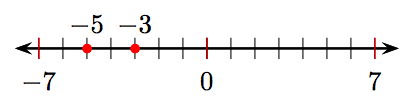
13.
i) Arrange the integers 6, 1, −3, and −5 on a number line.
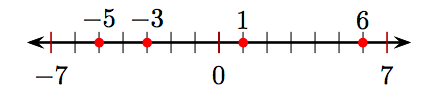
ii) −5, −3, 1, 6
15.
i) Arrange the integers 5, −6, 0, and 2 on a number line.
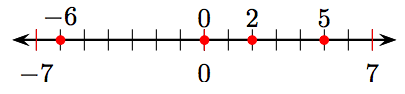
ii) −6, 0, 2, 5
17.
i) Arrange the integers −3, −5, 3, and 5 on a number line.
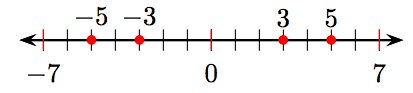
ii) −5, −3, 3, 5
19.
i) Arrange the integers −5, 4, 2, and −3 on a number line.
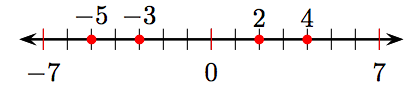
ii) −5, −3, 2, 4
21.
i) Arrange the integers 3, 5, −5 and −1 on a number line.
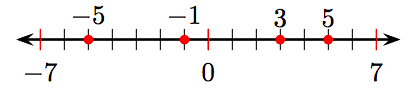
ii) −5, −1, 3, 5
23.
i) Arrange the integers −2, −4, 3, and −6 on a number line.
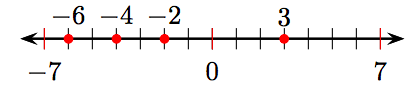
ii) −6, −4, −2, 3
25. −4 <0
27. −2 < −1
29. −3 < −1
31. 3 < 6
33. −3 > −6
35. −1 < 4
37. 4
39. 7
41. 5
43. −11
45. 5
47. −20
49. 4
51. 2
53. 0 and 4.
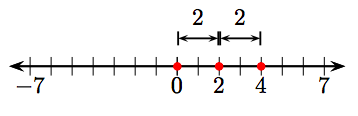
55. −7 and 1.
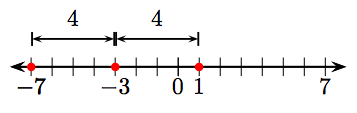
57. −5 and 1.
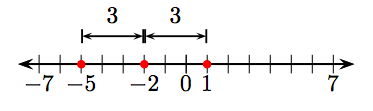
59. 1 and 5.
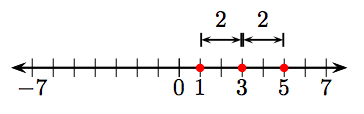
61. −3 and 3.
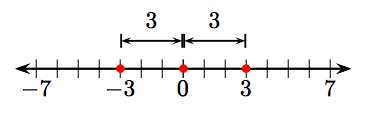
63. −2 and 2.
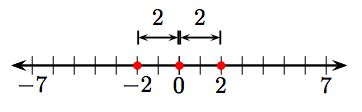
65. 2,350 feet
67.
| Month | Profit/Loss |
| Jan | 8 |
| Feb | −4 |
| Mar | −3 |
| Apr | −2 |
| May | 2 |
| Jun | 5 |
69. Approximately −8◦ Fahrenheit on January 16.
71.