2.3.1: Adding and Subtracting Fractions
- Page ID
- 30978
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)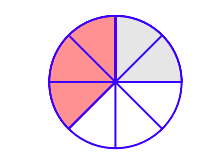Paul and Tony order a pizza which has been cut into eight equal slices. Thus, each slice is 1/8 of the whole pizza. Paul eats two slices (shaded in light gray in Figure \(\PageIndex{1}\)), or 2/8 of the whole pizza. Tony eats three slices (shaded in light red (or a darker shade of gray in black-and-white printing) in Figure \(\PageIndex{1}\)), or 3/8 of the whole pizza.
It should be clear that together Paul and Tony eat five slices, or 5/8 of the whole pizza. This reflects the fact that
\[ \frac{2}{8} + \frac{3}{8} = \frac{5}{8}.\nonumber \]
This demonstrates how to add two fractions with a common (same) denominator. Keep the common denominator and add the numerators. That is,
\[ \begin{align*} \frac{2}{8} + \frac{3}{8} &= \frac{2 + 3}{8} ~ && \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{5}{8} ~ && \textcolor{red}{ \text{ Simplify numerator.}} \end{align*} \]
Let a/c and b/c be two fractions with a common (same) denominator. Their sum is defined as
\[ \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\nonumber \]
That is, to add two fractions having common denominators, keep the common denominator and add their numerators.
A similar rule holds for subtraction.
Let a/c and b/c be two fractions with a common (same) denominator. Their difference is defined as
\[ \frac{a}{c} - \frac{b}{c} = \frac{a-b}{c}.\nonumber \]
That is, to subtract two fractions having common denominators, keep the common denominator and subtract their numerators.
Find the sum of 4/9 and 3/9.
Solution
Keep the common denominator and add the numerators.
\[ \begin{aligned} \frac{4}{9} + \frac{3}{9} &= \frac{4+3}{9} ~ & \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{7}{9} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Add:
\[ \frac{1}{8} + \frac{2}{8}\nonumber \]
- Answer
-
3/8
Subtract 5/16 from 13/16.
Solution
Keep the common denominator and subtract the numerators.
\[ \begin{aligned} \frac{13}{16} - \frac{5}{16} &= \frac{13-5}{16} ~ & \textcolor{red}{ \text{ Keep denominator; subtract numerators.}} \\ &=\frac{8}{16} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Of course, as we learned in Section 4.1, we should always reduce our final answer to lowest terms. One way to accomplish that in this case is to divide numerator and denominator by 8, the greatest common divisor of 8 and 16.
\[ \begin{aligned} = \frac{8 \div 8}{16 \div 8} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 8.}} \\ = \frac{1}{2} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Subtract:
\[ \frac{11}{12} - \frac{7}{12}\nonumber \]
- Answer
-
1/3
Simplify:
\[ \frac{3}{x} - \left( - \frac{7}{x} \right) .\nonumber \]
Solution
Both fractions share a common denominator.
\[ \begin{aligned} \frac{3}{x} - \left( - \frac{7}{x} \right) &= \frac{3}{x} + \frac{7}{x} ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ &= \frac{3+7}{x} ~ & \textcolor{red}{ \text{ Keep denominator, add numerators.}} \\ &= \frac{10}{x} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Adding Fractions with Different Denominators
Consider the sum
\[ \frac{4}{9} + \frac{1}{6}.\nonumber \]
We cannot add these fractions because they do not have a common denominator. So, what to do?
In order to add two fractions with different denominators, we need to:
- Find a common denominator for the given fractions.
- Make fractions with the common denominator that are equivalent to the original fractions.
If we accomplish the two items in the “Goal,” we will be able to find the sum of the given fractions.
So, how to start? We need to find a common denominator, but not just any common denominator. Let’s agree that we want to keep the numbers as small as possible and find a least common denominator.
The least common denominator (LCD) for a set of fractions is the smallest number divisible by each of the denominators of the given fractions.
Consider again the sum we wish to find:
\[ \frac{4}{9} + \frac{1}{6} .\nonumber \]
The denominators are 9 and 6. We wish to find a least common denominator, the smallest number that is divisible by both 9 and 6. A number of candidates come to mind: 36, 54, and 72 are all divisible by 9 and 6, to name a few. But the smallest number that is divisible by both 9 and 6 is 18. This is the least common denominator for 9 and 6.
We now proceed to the second item in “Goal.” We need to make fractions having 18 as a denominator that are equivalent to 4/9 and 1/6. In the case of 4/9, if we multiply both numerator and denominator by 2, we get
\[ \begin{aligned} \frac{4}{9} &= \frac{4 \cdot 2}{9 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 2.}} \\ &= \frac{8}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
In the case of 1/6, if we multiply both numerator and denominator by 3, we get
\[ \begin{aligned} \frac{1}{6} &= \frac{1 \cdot 3}{6 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 3.}} \\ &= \frac{3}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Typically, we’ll arrange our work as follows.
\[ \begin{aligned} \frac{4} + \frac{1}{6} &= \frac{4 \cdot \textcolor{red}{2}}{9 \cdot \textcolor{red}{2}} + \frac{1 \cdot \textcolor{red}{3}}{6 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 18.}} \\ &= \frac{8}{18} + \frac{3}{18} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{8+3}{18} ~ & \textcolor{red}{ \text{ Keep common denominator; add numerators.}} \\ &= \frac{11}{18} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Let’s summarize the procedure.
- Find the LCD, the smallest number divisible by all the denominators of the given fractions.
- Create fractions using the LCD as the denominator that are equivalent to the original fractions.
- Add or subtract the resulting equivalent fractions. Simplify, including reducing the final answer to lowest terms.
Simplify: \( \displaystyle \frac{3}{5} - \frac{2}{3}\).
Solution
The smallest number divisible by both 5 and 3 is 15.
\[ \begin{aligned} \frac{3}{5} - \frac{2}{3} &= \frac{3 \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} - \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ &= \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{9-10}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-1}{15} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Although this answer is perfectly acceptable, negative divided by positive gives us a negative answer, so we could also write
\[ = - \frac{1}{15}.\nonumber \]
Subtract:
\[ \frac{3}{4} - \frac{7}{5}\nonumber \]
- Answer
-
-13/20
Simplify: \(-\frac{1}{4} - \frac{5}{6}\).
Solution
The smallest number divisible by both 4 and 6 is 12.
\[ \begin{aligned} -\frac{1}{4} - \frac{5}{6} &= - \frac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} - \frac{5 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD =12.}} \\ &= - \frac{3}{12} - \frac{10}{12} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{-3-10}{12} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-13}{12} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Subtract: \(-\frac{3}{8} - \frac{1}{12}\)
- Answer
-
-11/24
Simplify: \(\frac{5}{x} + \frac{3}{4}\).
Solution
The smallest number divisible by both 4 and x is 4x.
\[ \begin{aligned} \frac{5}{x} + \frac{3}{4} = \frac{5 \cdot \textcolor{red}{4}}{x \cdot \textcolor{red}{4}} + \frac{3 \cdot \textcolor{red}{x}}{4 \cdot \textcolor{red}{x}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = }4x.} \\ = = \frac{20}{4x} + \frac{3x}{4x} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{20 + 3x}{4x} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]
Add:
\[ \frac{5}{z} + \frac{2}{3}\nonumber \]
- Answer
-
\[ \frac{15+2z}{3z}\nonumber \]
Simplify: \(\frac{2}{3}- \frac{x}{5}\).
Solution
The smallest number divisible by both 3 and 5 is 15.
\[ \begin{aligned} \frac{2}{3} - \frac{x}{5} = \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} - \frac{x \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ = \frac{10}{15} - \frac{3x}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{10 - 3x}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \end{aligned}\nonumber \]
Least Common Multiple
First we define the multiple of a number.
The multiples of a number d are 1d, 2d, 3d, 4d, etc. That is, the multiples of d are the numbers nd, where n is a natural number.
For example, the multiples of 8 are 1 · 8, 2 · 8, 3 · 8, 4 · 8, etc., or equivalently, 8, 16, 24, 32, etc.
The least common multiple (LCM) of a set of numbers is the smallest number that is a multiple of each number of the given set. The procedure for finding an LCM follows:
- List all of the multiples of each number in the given set of numbers.
- List the multiples that are in common.
- Pick the least of the multiples that are in common.
Find the least common multiple (LCM) of 12 and 16.
Solution
List the multiples of 12 and 16.
Multiples of 12 : 12, 24, 36, 48, 60, 72, 84, 96,...
Multiples of 16 : 16, 32, 48, 64, 80, 96, 112,...
Pick the common multiples.
Common Multiples : 48, 96,...
The LCM is the least of the common multiples.
LCM(12,16) = 48
Find the least common denominator of 6 and 9.
- Answer
-
18
The least common denominator is the least common multiple of the denominators.
For example, suppose your problem is 5/12 + 5/16. The LCD is the smallest number divisible by both 12 and 16. That number is 48, which is also the LCM of 12 and 16. Therefore, the procedure for finding the LCM can also be used to find the LCD.
Least Common Multiple Using Prime Factorization
You can also find the LCM using prime factorization.
To find an LCM for a set of numbers, follow this procedure:
- Write down the prime factorization for each number in compact form using exponents.
- The LCM is found by writing down every factor that appears in step 1 to the highest power of that factor that appears.
Use prime factorization to find the least common multiple find the least common denominator of 18 and 24. (LCM) of 12 and 16.
Solution
Prime factor 12 and 16.
\[ \begin{aligned} 12 = 2 \cdot 2 \cdot 3 \\ 16 = 2 \cdot 2 \cdot 2 \cdot 2 \end{aligned}\nonumber \]
Write the prime factorizations in compact form using exponents.
\[ \begin{aligned} 12 = 2^2 \cdot 3^1 \\ 16 = 2^4 \end{aligned}\nonumber \]
To find the LCM, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2 and 3. The highest power of 2 that appears is 24. The highest power of 3 that appears is 31.
\[ \begin{aligned} \text{LCM} = 2^4 \cdot 3^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \end{aligned}\nonumber \]
Now we expand this last expression to get our LCM.
\[ \begin{aligned} = 16 \cdot 3 ~ & \textcolor{red}{ \text{ Expand: } 2^4 = 16 \text{ and } 3^1 = 3.} \\ = 48. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Note that this answer is identical to the LCM found in Example 8 that was found by listing multiples and choosing the smallest multiple in common.
Use prime factorization to find the least common denominator of 18 and 24.
- Answer
-
72
Simplify: \(\frac{5}{28} + \frac{11}{42}\).
Solution
Prime factor the denominators in compact form using exponents.
28 = 2 · 2 · 7=22 · 7
42 = 2 · 3 · 7=21 · 31 · 71
To find the LCD, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2, 3, and 7. The highest power of 2 that appears is 22. The highest power of 3 that appears is 31. The highest power of 7 that appears is 71.
\[ \begin{aligned} \text{LCM} = 2^2 \cdot 3^1 \cdot 7^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 4 \cdot 3 \cdot 7 ~ & \textcolor{red}{ \text{ Expand: } 2^2 = 4, ~ 3^1 = 3, ~ 7^1 = 7.} \\ = 84 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Create equivalent fractions with the new LCD, then add.
\[ \begin{aligned} \frac{5}{28} + \frac{11}{42} = \frac{5 \cdot \textcolor{red}{3}}{28 \cdot \textcolor{red}{3}} + \frac{11 \cdot \textcolor{red}{2}}{42 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 84.}} \\ = \frac{15}{84} + \frac{22}{84} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{37}{84} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]
Simplify: \( \frac{5}{24} + \frac{5}{36}\)
- Answer
-
25/72
Simplify: \(- \frac{11}{24} - \frac{1}{18}\).
Solution
Prime factor the denominators in compact form using exponents.
24 = 2 · 2 · 2 · 3=23 · 31
18 = 2 · 3 · 3=21 · 32
To find the LCD, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2 and 3. The highest power of 2 that appears is 23. The highest power of 3 that appears is 32.
\[ \begin{aligned} \text{LCM} = 2^3 \cdot 3^2 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 8 \cdot 9 ~ & \textcolor{red}{ \text{ Expand: } 2^3 = 8 \text{ and } 3^2 = 9.} \\ = 72. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Create equivalent fractions with the new LCD, then subtract.
\[ \begin{aligned} - \frac{11}{24} - \frac{1}{18} = - \frac{11 \cdot \textcolor{red}{3}}{24 \cdot \textcolor{red}{3}} - \frac{1 \cdot \textcolor{red}{4}}{18 \cdot \textcolor{red}{4}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 72.}} \\ = - \frac{33}{72} - \frac{4}{72} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{-33-4}{72} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ = \frac{-37}{72} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]
Of course, negative divided by positive yields a negative answer, so we can also write our answer in the form
\[ - \frac{11}{24} - \frac{1}{18} = - \frac{37}{72}.\nonumber \]
Simplify: \( - \frac{5}{24} - \frac{11}{36}\)
- Answer
-
−37/72
Comparing Fractions
The simplest way to compare fractions is to create equivalent fractions.
Arrange the fractions −1/2 and −4/5 on a number line, then compare them by using the appropriate inequality symbol.
Solution
The least common denominator for 2 and 5 is the number 10. First, make equivalent fractions with a LCD equal to 10.
\[ \begin{array}{c} - \frac{1}{2} = - \frac{1 \cdot \textcolor{red}{5}}{2 \cdot \textcolor{red}{5}} = - \frac{5}{10} \\ - \frac{4}{5} = - \frac{4 \cdot \textcolor{red}{2}}{5 \cdot \textcolor{red}{2}} = - \frac{8}{10} \end{array}\nonumber \]
To plot tenths, subdivide the interval between −1 and 0 into ten equal increments.
Because −4/5 lies to the left of −1/2, we have that −4/5 is less than −1/2, so we write
\[ - \frac{4}{5} < - \frac{1}{2}.\nonumber \]
Compare −3/8 and −1/2.
- Answer
-
\[ - \frac{1}{2} < - \frac{3}{8}\nonumber \]
Exercises
In Exercises 1-10, list the multiples the given numbers, then list the common multiples. Select the LCM from the list of common multiples.
1. 9 and 15
2. 15 and 20
3. 20 and 8
4. 15 and 6
5. 16 and 20
6. 6 and 10
7. 20 and 12
8. 12 and 8
9. 10 and 6
10. 10 and 12
In Exercises 11-20, for the given numbers, calculate the LCM using prime factorization.
11. 54 and 12
12. 108 and 24
13. 18 and 24
14. 36 and 54
15. 72 and 108
16. 108 and 72
17. 36 and 24
18. 18 and 12
19. 12 and 18
20. 12 and 54
In Exercises 21-32, add or subtract the fractions, as indicated, and simplify your result.
21. \(\frac{7}{12} − \frac{1}{12}\)
22. \(\frac{3}{7} − \frac{5}{7}\)
23. \(\frac{1}{9} + \frac{1}{9}\)
24. \(\frac{1}{7} + \frac{3}{7}\)
25. \(\frac{1}{5} − \frac{4}{5}\)
26. \(\frac{3}{5} − \frac{2}{5}\)
27. \(\frac{3}{7} − \frac{4}{7}\)
28. \(\frac{6}{7} − \frac{2}{7}\)
29. \(\frac{4}{11} + \frac{9}{11}\)
30. \(\frac{10}{11} + \frac{4}{11}\)
31. \(\frac{3}{11} + \frac{4}{11}\)
32. \(\frac{3}{7} + \frac{2}{7}\)
In Exercises 33-56, add or subtract the fractions, as indicated, and simplify your result.
33. \(\frac{1}{6} − \frac{1}{8}\)
34. \(\frac{7}{9} − \frac{2}{3}\)
35. \(\frac{1}{5} + \frac{2}{3}\)
36. \(\frac{7}{9} + \frac{2}{3}\)
37. \(\frac{2}{3} + \frac{5}{8}\)
38. \(\frac{3}{7} + \frac{5}{9}\)
39. \(\frac{4}{7} − \frac{5}{9}\)
40. \(\frac{3}{5} − \frac{7}{8}\)
41. \(\frac{2}{3} − \frac{3}{8}\)
42. \(\frac{2}{5} − \frac{1}{8\)
43. \(\frac{6}{7} − \frac{1}{6}\)
44. \(\frac{1}{2} − \frac{1}{4}\)
45. \(\frac{1}{6} + \frac{2}{3}\)
46. \(\frac{4}{9} + \frac{7}{8}\)
47. \(\frac{7}{9} + \frac{1}{8}\)
48. \(\frac{1}{6} + \frac{1}{7}\)
49. \(\frac{1}{3} + \frac{1}{7}\)
50. \(\frac{5}{6} + \frac{1}{4}\)
51. \(\frac{1}{2} − \frac{2}{7}\)
52. \(\frac{1}{3} − \frac{1}{8}\)
53. \(\frac{5}{6} − \frac{4}{5}\)
54. \(\frac{1}{2} − \frac{1}{9}\)
55. \(\frac{1}{3} + \frac{1}{8}\)
56. \(\frac{1}{6} + \frac{7}{9}\)
In Exercises 57-68, add or subtract the fractions, as indicated, by first using prime factorization to find the least common denominator.
57. \(\frac{7}{36} + \frac{11}{54}\)
58. \(\frac{7}{54} + \frac{7}{24}\)
59. \(\frac{7}{18} − \frac{5}{12}\)
60. \(\frac{5}{54} − \frac{7}{12}\)
61. \(\frac{7}{36} + \frac{7}{54}\)
62. \(\frac{5}{72} + \frac{5}{108}\)
63. \(\frac{7}{24} − \frac{5}{36}\)
64. \(\frac{11}{54} + \frac{7}{72}\)
65. \(\frac{11}{12} + \frac{5}{18}\)
66. \(\frac{11}{24} + \frac{11}{108}\)
67. \(\frac{11}{54} − \frac{5}{24}\)
68. \(\frac{7}{54} − \frac{5}{24}\)
In Exercises 69-80, add or subtract the fractions, as indicated, and simplify your result.
69. \(\frac{−3}{7} + \left( \frac{−3}{7} \right)\)
70. \(\frac{−5}{9} + \left( \frac{−1}{9} \right)\)
71. \(\frac{7}{9} − \left( \frac{−1}{9} \right) \)
72. \(\frac{8}{9} − \left( \frac{−4}{9} \right)\)
73. \(\frac{7}{9} + \left( \frac{−2}{9} \right)\)
74. \( \frac{2}{3} + \left( \frac{−1}{3} \right)\)
75. \(\frac{−3}{5} − \frac{4}{5}\)
76. \(\frac{−7}{9} − \frac{1}{9}\)
77. \(\frac{−7}{8} + \frac{1}{8}\)
78. \(\frac{−2}{3} + \(\frac{1}{3}\)
79. \(\frac{−1}{3} − \left( \frac{−2}{3} \right)\)
80. \(\frac{−7}{8} − \left( \frac{−5}{8} \right)\)
In Exercises 81-104, add or subtract the fractions, as indicated, and simplify your result.
81. \(\frac{−2}{7}\) + \frac{4}{5}\)
82. \(\frac{−1}{4} + \frac{2}{7}\)
83. \(\frac{−1}{4} − \left( \frac{−4}{9} \right)\)
84. \(\frac{−3}{4} −left( \frac{−1}{8} \right)\)
85. \(\frac{−2}{7} + \frac{3}{4}\)
86. \(\frac{−1}{3} + \frac{5}{8}\)
87. \(\frac{−4}{9} − \frac{1}{3}\)
88. \(\frac{−5}{6} − \frac{1}{3}\)
89. \(\frac{−5}{7} − \left( \frac{−1}{5} \right)\)
90. \(\frac{−6}{7} − \left( \frac{−1}{8} \right)\)
91. \(\frac{1}{9} + \left( \frac{−1}{3} \right)\)
92. \(\frac{1}{8} + \left( \frac{−1}{2} \right)\)
93. \(\frac{2}{3} + \left( \frac{−1}{9} \right)\)
94. \(\frac{3}{4} + \left( \frac{−2}{3} \right)\)
95. \(\frac{−1}{2} + \left( \frac{−6}{7} \right)\)
96. \(\frac{−4}{5} + \left( \frac{−1}{2} \right)\)
97. \(\frac{−1}{2} + \left( \frac{−3}{4} \right)\)
98. \(\frac{−3}{5} + \left( \frac{−1}{2} \right)\)
99. \(\frac{−1}{4} − \frac{1}{2}\)
100. \(\frac{−8}{9} − \frac{2}{3}\)
101. \(\frac{5}{8} − \left( \frac{−3}{4} \right)\)
102. \(\frac{3}{4} − \left( \frac{−3}{8} \right)\)
103. \(\frac{1}{8} − \left( \frac{−1}{3} \right)\)
104. \(\frac{1}{2} − \left( \frac{−4}{9} \right)\)
In Exercises 105-120, add or subtract the fractions, as indicated, and write your answer is lowest terms.
105. \(\frac{1}{2} + \frac{3q}{5}\)
106. \(\frac{4}{7} − \frac{b}{3}\)
107. \(\frac{4}{9} − \frac{3a}{4}\)
108. \(\frac{4}{9} − \frac{b}{2}\)
109. \(\frac{2}{s} + \frac{1}{3}\)
110. \(\frac{2}{s} + \frac{3}{7}\)
111. \(\frac{1}{3} − \frac{7}{b}\)
112. \(\frac{1}{2} − \frac{9}{s}\)
113. \(\frac{4b}{7} + \frac{2}{3}\)
114. \(\frac{2a}{5} + \frac{5}{8}\)
115. \(\frac{2}{3} − \frac{9}{t}\)
116. \(\frac{4}{7} − \frac{1}{y}\)
117. \(\frac{9}{s} + \frac{7}{8}\)
118. \(\frac{6}{t} − \frac{1}{9}\)
119. \(\frac{7b}{8} − \frac{5}{9}\)
120. \(\frac{3p}{4} − \frac{1}{8}\)
In Exercises 121-132, determine which of the two given statements is true.
121. \(\frac{−2}{3} < \frac{−8}{7}\) or \(\frac{− 2}{3} > \frac{−8}{7}\)
122. \(\frac{−1}{7} < \frac{−8}{9}\) or \(\frac{− 1}{7} > \frac{−8}{9}\)
123. \(\frac{6}{7} < \frac{7}{3}\) or \(\frac{6}{7} > \frac{7}{3}\)
124. \(\frac{1}{2} < \frac{2}{7}\) or \(\frac{1}{2} > \frac{2}{7}\)
125. \(\frac{−9}{4} < \frac{−2}{3}\) or \frac{− 9}{4} > \frac{−2}{3}\)
126. \(\frac{−3}{7} < \frac{−9}{2}\) or \(\frac{− 3}{7} > \frac{−9}{2}\)
127. \(\frac{5}{7} < \frac{5}{9}\) or \frac{5}{7} > \frac{5}{9}\)
128. \(\frac{1}{2} < \frac{1}{3}\) or \(\frac{1}{2} > \frac{1}{3}\)
129. \(\frac{−7}{2} < \frac{−1}{5}\) or \(\frac{− 7}{2} > \frac{−1}{5}\)
130. \(\frac{−3}{4} < \frac{−5}{9}\) or \(\frac{− 3}{4} > \frac{−5}{9}\)
131. \(\frac{5}{9} < \frac{6}{5}\) or \(\frac{5}{9} > \frac{6}{5}\)
132. \(\frac{3}{2} < \frac{7}{9}\) or \(\frac{3}{2} > \frac{7}{9}\)
Answers
1. 45
3. 40
5. 80
7. 60
9. 30
11. 108
13. 72
15. 216
17. 72
19. 36
21. \(\frac{1}{2}\)
23. \(\frac{2}{9}\)
25. \(\frac{−3}{5}\)
27. \(\frac{−1}{7}\)
29. \(\frac{13}{11}\)
31. \(\frac{7}{11}\)
33. \(\frac{1}{24}\)
35. \(\frac{13}{15}\)
37. \(\frac{31}{24}\)
39. \(\frac{1}{63}\)
41. \(\frac{7}{24}\)
43. \(\frac{29}{42}\)
45. \(\frac{5}{6}\)
47. \(\frac{65}{72}\)
49. \(\frac{10}{21}\)
51. \(\frac{3}{14}\)
53. \(\frac{1}{30}\)
55. \(\frac{11}{24}\)
57. \(\frac{43}{108}\)
59. \(\frac{−1}{36}\)
61. \(\frac{35}{108}\)
63. \(\frac{11}{72}\)
65. \(\frac{43}{36}\)
67. \(\frac{−1}{216}\)
69. \(\frac{−6}{7}\)
71. \(\frac{8}{9}\)
73. \(\frac{5}{9}\)
75. \(\frac{− 7}{5}\)
77. \(\frac{− 3}{4}\)
79. \(\frac{1}{3}\)
81. \(\frac{18}{35}\)
83. \(\frac{7}{36}\)
85. \(\frac{13}{28}\)
87. \(\frac{− 7}{9}\)
89. \(\frac{−18}{35}\)
91. \(\frac{− 2}{9}\)
93. \(\frac{5}{9}\)
95. \(\frac{−19}{14}\)
97. \(\frac{− 5}{4}\)
99. \(\frac{− 3}{4}\)
101. \(\frac{11}{8}\)
103. \(\frac{11}{24}\)
105. \(\frac{5+6 q}{10}\)
107. \(\frac{16 − 27 a}{36}\)
109. \(\frac{6 + s}{3 s}\)
111. \(\frac{b − 21}{3b}\)
113. \(\frac{12 b + 14}{21}\)
115. \(\frac{2 t − 27}{3t}\)
117. \(\frac{72 + 7 s}{8 s}\)
119. \(\frac{63 b − 40}{72}\)
121. \(\frac{− 2}{3} > \(\frac{− 8}{7}\)
123. \(\frac{6}{7} < \frac{7}{3}\)
125. \(\frac{− 9}{4} < \frac{− 2}{3}\)
127. \(\frac{5}{7} > \frac{5}{9}\)
129. \(\frac{− 7}{2 } < \frac{− 1}{5}\)
131. \(\frac{5}{9} < \frac{6}{5}\)