Multiplying decimal numbers involves two steps: (1) multiplying the numbers as whole numbers, ignoring the decimal point, and (2) placing the decimal point in the correct position in the product or answer.
For example, consider (0.7)(0.08), which asks us to find the product of “seven tenths” and “eight hundredths.” We could change these decimal numbers to fractions, then multiply.
\[ \begin{aligned} (0.7)(0.8) & = \frac{7}{10} \cdot \frac{8}{100} \\ & = \frac{56}{100} \\ & = 0.056 \end{aligned}\nonumber \]
The product is 56/1000, or “fifty six thousandths,” which as a decimal is written 0.056.
Important Observations
There are two very important observations to be made about the example (0.7)(0.08).
1. In fractional form
\[\frac{7}{10} \cdot \frac{8}{100} = \frac{56}{1000},\nonumber \]
note that the numerator of the product is found by taking the product of the whole numbers 7 and 8. That is, you ignore the decimal points in 0.7 and 0.08 and multiply 7 and 8 as if they were whole numbers.
2. The first factor, 0.7, has one digit to the right of the decimal point. Its fractional equivalent, 7/10, has one zero in its denominator. The second factor, 0.08, has two digits to the right of the decimal point. Its fractional equivalent, 8/100, has two zeros in its denominator. Therefore, the product 56/1000 is forced to have three zeros in its denominator and its decimal equivalent, 0.056, must therefore have three digits to the right of the decimal point.
Let’s look at another example.
Example 1
Simplify: (2.34)(1.2).
Solution
Change the decimal numbers “two and thirty four hundredths” and “one and two tenths” to fractions, then multiply.
\[ \begin{aligned} (2.34)(1.2) = 2 \frac{34}{100} \cdot 1 \frac{2}{10} ~ & \textcolor{red}{ \text{ Change decimals to fractions.}} \\ = \frac{234}{100 \cdot \frac{12}{10} ~ & \textcolor{red}{ \text{ Change mixed to improper fractions.}} \\ = \frac{2808}{1000} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 2 \frac{808}{1000} ~ & \textcolor{red}{ \text{ Change to mixed fraction.}} \\ = 2.808 ~ & \textcolor{red}{ \text{ Change back to decimal form.}} \end{aligned}\nonumber \]
Exercise
Multiply: (1.86)(9.5)
- Answer
-
17.67
The Circumference of a Circle
When we work with polygons, the perimeter of the polygon is found by summing the lengths of its edges. The circle uses a different name for its perimeter.
The Circumference of a Circle
The length of the circle is called its circumference. We usually use the variable C to denote the circumference of a circle
That is, if one were to walk along the circle, the total distance traveled in one revolution is the circumference of the circle.
The ancient mathematicians of Egypt and Greece noted a striking relation between the circumference of a circle and its diameter. They discovered that whenever you divide a circle’s circumference by its diameter, you get a constant. That is, if you take a very large circle and divide its circumference by its diameter, you get exactly the same number if you take a very small circle and divide its circumference by its diameter. This common constant was named π (“pi”).
Relating the Circumference and Diameter
Whenever a circle’s circumference is divided by its diameter, the answer is the constant π. That is, if C is the circumference of the circle and d is the circle’s diameter, then
\[\frac{C}{d} = \pi.\nonumber \]
In modern times, we usually multiply both sides of this equation by d to obtain the formula for the circumference of a circle.
\[C = \pi d\nonumber \]
Because the diameter of a circle is twice the length of its radius, we can substitute d = 2r in the last equation to get an alternate form of the circumference equation.
\[C = \pi (2r) = 2 \pi r\nonumber \]
The number π has a rich and storied history. Ancient geometers from Egypt, Babylonia, India, and Greece knew that π was slightly larger than 3. The earliest known approximations date from around 1900 BC (Wikipedia); they are 25/8 (Babylonia) and 256/81 (Egypt). The Indian text Shatapatha Brahmana gives π as 339/108 ≈ 3.139. Archimedes (287-212 BC) was the first to estimate π rigorously, approximating the circumference of a circle with inscribed and circumscribed polygons. He was able to prove that 223/71 < π < 22/7. Taking the average of these values yields π ≈ 3.1419. Modern mathematicians have proved that π is an irrational number, an infinite decimal that never repeats any pattern. Mathematicians, with the help of computers, routinely produce approximations of π with billions of digits after the decimal point.
Digits of Pi
Here is π, correct to the first fifty digits.
π = 3.14159265358979323846264338327950288419716939937510 ...
The number of digits of π used depends on the application. Working at very small scales, one might keep many digits of π, but if you are building a circular garden fence in your backyard, then fewer digits of π are needed.
Example 9
Find the circumference of a circle given its radius is 12 feet.
Solution
The circumference of the circle is given by the formula C = πd, or, because d = 2r,
\[C = 2πr.\nonumber \]
Substitute 12 for r.
\[C = 2πr = 2π(12) = 24π\nonumber \]
Therefore, the circumference of the circle is exactly C = 24π feet.
We can approximate the circumference by entering an approximation for π. Let’s use π ≈ 3.14. Note: The symbol ≈ is read “approximately equal to.”
\[C = 24π ≈ 24(3.14) ≈ 75.36 \text{ feet}\nonumber \]
It is important to understand that the solution C = 24π feet is the exact circumference, while C ≈ 75.36 feet is only an approximation.
Exercise
Find the radius of a circle having radius 14 inches. Use π ≈ 3.14
- Answer
-
87.92 inches
The Area of a Circle
Here’s a reasonable argument used to help develop a formula for the area of a circle. Start with a circle of radius r and divide it into 8 equal wedges, as shown in the figure that follows.
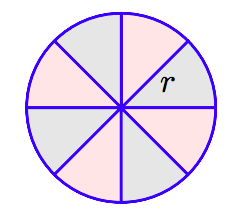
Rearrange the pieces as shown in the following figure.
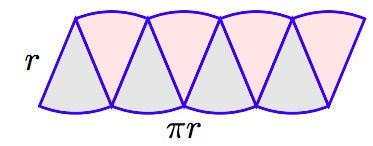
Note that the rearranged pieces almost form a rectangle with length approximately half the circumference of the circle, πr, and width approximately r. The area would be approximately A ≈ (length)(width) ≈ (πr)(r) ≈ πr2. This approximation would be even better if we doubled the number of wedges of the circle.
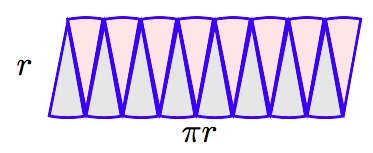
If we doubled the number of wedges again, the resulting figure would even more closely resemble a rectangle with length πr and width r. This leads to the following conclusion.
The Area of a Circle
The area of a circle of radius r is given by the formula
\[A = \pi r^2.\nonumber \]
Example 10
Find the area of a circle having a diameter of 12.5 meters. Use 3.14 for π and round the answer for the area to the nearest tenth of a square meter.
Solution
The diameter is twice the radius.
\[d = 2r\nonumber \]
Substitute 12.5 for d and solve for r.
\[ \begin{aligned} 12.5 = 2r ~ & \textcolor{red}{ \text{ Substitute 12.5 for } d.} \\ \frac{12.5}{2} = \frac{2r}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 6.25 = r ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, the radius is 6.25 meters. To find the area, use the formula
\[A = \pi r^2\nonumber \]
and substitute: 3.14 for π and 6.25 for r.
\[ \begin{aligned} A = (3.14)(6.25)^2 ~ & \textcolor{red}{ \text{ Substitute: 3.14 for } \pi, \text{ 6.25 for } r.} \\ = (3.14)(39.0625) ~ & \textcolor{red}{ \text{ Square first: } (6.25)^2 = 39.0625} \\ =122.65625 ~ & \textcolor{red}{ \text{ Multiply: } (3.14)(39.0625) = 122.65625} \end{aligned}\nonumber \]
Hence, the approximate area of the circle is A = 122.65625 square meters. To round to the nearest tenth of a square meter, identify the rounding digit and the test digit.
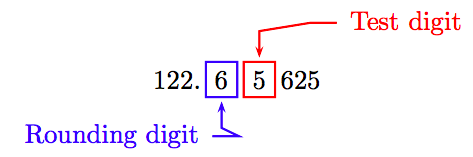
Because the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate. Thus, correct to the nearest tenth of a square meter, the area of the circle is approximately
\[A ≈ 122.7 \text{ m}^2.\nonumber \]
Exercise
Find the area of a circle having radius 12.2 centimeters. Use π ≈ 3.14
- Answer
-
467.3576 cm2
Exercises
In Exercises 1-28, multiply the decimals.
1. (6.7)(0.03)
2. (2.4)(0.2)
3. (28.9)(5.9)
4. (33.5)(2.1)
5. (4.1)(4.6)
6. (2.6)(8.2)
7. (75.3)(0.4)
8. (21.4)(0.6)
9. (6.98)(0.9)
10. (2.11)(0.04)
11. (57.9)(3.29)
12. (3.58)(16.3)
13. (47.3)(0.9)
14. (30.7)(0.4)
15. (9.9)(6.7)
16. (7.2)(6.1)
17. (19.5)(7.9)
18. (43.4)(8.9)
19. (6.9)(0.3)
20. (7.7)(0.7)
21. (35.3)(3.81)
22. (5.44)(9.58)
23. (2.32)(0.03)
24. (4.48)(0.08)
25. (3.02)(6.7)
26. (1.26)(9.4)
27. (4.98)(6.2)
28. (3.53)(2.9)
In Exercises 29-56, multiply the decimals.
29. (−9.41)(0.07)
30. (4.45)(−0.4)
31. (−7.4)(−0.9)
32. (−6.9)(0.05)
33. (−8.2)(3.7)
34. (−7.5)(−6.6)
35. (9.72)(−9.1)
36. (6.22)(−9.4)
37. (−6.4)(2.6)
38. (2.3)(−4.4)
39. (−39.3)(−0.8)
40. (57.7)(−0.04)
41. (63.1)(−0.02)
42. (−51.1)(−0.8)
43. (−90.8)(3.1)
44. (−74.7)(2.9)
45. (47.5)(−82.1)
46. (−14.8)(−12.7)
47. (−31.1)(−4.8)
48. (−28.7)(−6.8)
49. (−2.5)(−0.07)
50. (−1.3)(−0.05)
51. (1.02)(−0.2)
52. (−7.48)(−0.1)
53. (7.81)(−5.5)
54. (−1.94)(4.2)
55. (−2.09)(37.9)
56. (20.6)(−15.2)
In Exercises 57-68, multiply the decimal by the given power of 10.
57. 24.264 · 10
58. 65.722 · 100
59. 53.867 · 104
60. 23.216 · 104
61. 5.096 · 103
62. 60.890 · 103
63. 37.968 · 103
64. 43.552 · 103
65. 61.303 · 100
66. 83.837 · 1000
67. 74.896 · 1000
68. 30.728 · 100
In Exercises 69-80, simplify the given expression.
69. (0.36)(7.4) − (−2.8)2
70. (−8.88)(−9.2) − (−2.3)2
71. 9.4 − (−7.7)(1.2)2
72. 0.7 − (−8.7)(−9.4)2
73. 5.94 − (−1.2)(−1.8)2
74. −2.6 − (−9.8)(9.9)2
75. 6.3 − 4.2(9.3)2
76. 9.9 − (−4.1)(8.5)2
77. (6.3)(1.88) − (−2.2)2
78. (−4.98)(−1.7) − 3.52
79. (−8.1)(9.4) − 1.82
80. (−3.63)(5.2) − 0.82
81. Given a = −6.24, b = 0.4, and c = 7.2, evaluate the expression a − bc2.
82. Given a = 4.1, b = −1.8, and c = −9.5, evaluate the expression a − bc2.
83. Given a = −2.4, b = −2.1, and c = −4.6, evaluate the expression ab − c2.
84. Given a = 3.3, b = 7.3, and c = 3.4, evaluate the expression ab − c2.
85. Given a = −3.21, b = 3.5, and c = 8.3, evaluate the expression a − bc2.
86. Given a = 7.45, b = −6.1, and c = −3.5, evaluate the expression a − bc2.
87. Given a = −4.5, b = −6.9, and c = 4.6, evaluate the expression ab − c2.
88. Given a = −8.3, b = 8.2, and c = 5.4, evaluate the expression ab − c2.
89. A circle has a diameter of 8.56 inches. Using π ≈ 3.14, find the circumference of the circle, correct to the nearest tenth of an inch.
90. A circle has a diameter of 14.23 inches. Using π ≈ 3.14, find the circumference of the circle, correct to the nearest tenth of an inch.
91. A circle has a diameter of 12.04 inches. Using π ≈ 3.14, find the circumference of the circle, correct to the nearest tenth of an inch.
92. A circle has a diameter of 14.11 inches. Using π ≈ 3.14, find the circumference of the circle, correct to the nearest tenth of an inch.
93. A circle has a diameter of 10.75 inches. Using π ≈ 3.14, find the area of the circle, correct to the nearest hundredth of a square inch.
94. A circle has a diameter of 15.49 inches. Using π ≈ 3.14, find the area of the circle, correct to the nearest hundredth of a square inch.
95. A circle has a diameter of 13.96 inches. Using π ≈ 3.14, find the area of the circle, correct to the nearest hundredth of a square inch.
96. A circle has a diameter of 15.95 inches. Using π ≈ 3.14, find the area of the circle, correct to the nearest hundredth of a square inch.
97. Sue has decided to build a circular fish pond near her patio. She wants it to be 15 feet in diameter and 1.5 feet deep. What is the volume of water it will hold? Use π ≈ 3.14. Hint: The volume of a cylinder is given by the formula V = πr2h, which is the area of the circular base times the height of the cylinder.
98. John has a decision to make regarding his employment. He currently has a job at Taco Loco in Fortuna. After taxes, he makes about $9.20 per hour and works about 168 hours a month. He currently pays $400 per month for rent. He has an opportunity to move to Santa Rosa and take a job at Mi Ultimo Refugio which would pay $10.30 per hour after taxes for 168 hours a month, but his rent would cost $570 per month.
a) After paying for housing in Fortuna, how much does he have left over each month for other expenditures?
b) After paying for housing in Santa Rosa, how much would he have left over each month for other expenditures?
c) For which job would he have more money left after paying rent and how much would it be?
99. John decided to move to Santa Rosa and take the job at Mi Ultimo Refugio (see Exercise 98). He was able to increase his income because he could work 4 Sundays a month at time-and-a half. So now he worked 32 hours a month at time-and-a-half and 136 hours at the regular rate of $10.30 (all after taxes were removed). Note: He previously had worked 168 hours per month at $10.30 per hour.
a) What was his new monthly income?
b) How much did his monthly income increase?
100. Electric Bill. On a recent bill, PGE charged $0.11531 per Kwh for the first 333 Kwh of electrical power used. If a household used 312 Kwh of power, what was their electrical bill?
101. Cabernet. In Napa Valley, one acre of good land can produce about 3.5 tons of quality grapes. At an average price of $3,414 per ton for premium cabernet, how much money could you generate on one acre of cabernet farming? Associated Press-Times-Standard 03/11/10 Grape moth threatens Napa Valley growing method.
102. Fertilizer. Using the 2008 Ohio Farm Custom Rates, the average cost for spreading dry bulk fertilizer is about $4.50 per acre. What is the cost to fertilize 50 acres?
103. Agribusiness. Huge corporate agribarns house 1000 pigs each.
a) If each pig weighs approximately 100 pounds, how many pounds of pig is in each warehouse?
b) At an average $1.29 per pound, what is the total cash value for a corporate agribarn? Associated Press-Times-Standard 12/29/09 Pressure rises to stop antibiotics in agriculture.
104. Shipwrecks. A dozen centuries-old shipwrecks were found in the Baltic Sea by a gas company building an underwater pipeline between Russia and Germany. The 12 wrecks were found in a 30-mile-long and 1.2-mile-wide corridor at a depth of 430 feet. Model the corridor with a rectangle and find the approximate area of the region where the ships were found. Associated Press-Times-Standard 03/10/10 Centuries-old shipwrecks found in Baltic Sea.
105. Radio dish. The diameter of the “workhorse fleet” of radio telescopes, like the one in Goldstone, California, is 230 feet. What is the circumference of the radio telescope dish to the nearest tenth? Associated Press-Times-Standard 03/09/2010 NASA will repair deep space antenna in California desert.