4.4.2: Combining Like Terms
- Last updated
- Jan 8, 2020
- Save as PDF
- Page ID
- 31005
( \newcommand{\kernel}{\mathrm{null}\,}\)
We begin our discussion with the definition of a term.
Definition: Term
A term is a single number or variable, or it can be the product of a number (called its coefficient) and one or more variables (called its variable part). The terms in an algebraic expression are separated by addition symbols.
Example 1
Identify the terms in the algebraic expression
For each term, identify its coefficient and variable part.
Solution
In tabular form, we list each term of the expression 3x^2 + 5xy + 9y^2 + 12, its coefficient, and its variable part.
| Term | Coefficient | Variable Part |
|---|---|---|
| 3x2 | 3 | x2 |
| 5xy | 5 | xy |
| 9y2 | 9 | y2 |
| 12 | 12 | None |
Exercise
How many terms are in the algebraic expression 3x2 + 2xy − 3y2?
- Answer
-
3
Example 2
Identify the terms in the algebraic expression
For each term, identify its coefficient and variable part.
Solution
The first step is to write each difference as a sum, because the terms of an expression are defined above to be those items separated by addition symbols.
In tabular form, we list each term of the expression
| Term | Coefficient | Variable Part |
|---|---|---|
| a3 | 1 | a3 |
| -3a2b | −3 | a2b |
| 3ab2 | 3 | ab2 |
| −b3 | −1 | b3 |
Exercise
How many terms are in the algebraic expression
- Answer
-
4
Like Terms
We define what is meant by “like terms” and “unlike terms.”
Definition
Like and Unlike Terms. The variable parts of two terms determine whether the terms are like terms or unlike terms.
Like Terms. Two terms are called like terms if they have identical variable parts, which means that the terms must contain the same variables raised to the same exponential powers.
Unlike Terms. Two terms are called unlike terms if their variable parts are different.
Example 3
Classify each of the following pairs as either like terms or unlike terms: (a) 3x and −7x, (b) 2y and 3y2, (c) −3t and 5u, and (d) −4a3 and 3a3.
Solution
Like terms must have identical variable parts.
- 3x and −7x have identical variable parts. They are “like terms.”
- 2y and 3y2 do not have identical variable parts (the exponents differ). They are “unlike terms.”
- −3t and 5u do not have identical variable parts (different variables). They are “unlike terms.”
- −4a3 and 3a3 have identical variable parts. They are “like terms.”
Exercise
Are −3xy and 11xy like or unlike terms?
- Answer
-
Like terms
Combining Like Terms
When using the distributive property, it makes no difference whether the multiplication is on the left or the right, one still distributes the multiplication times each term in the parentheses.
Distributive Property
If a, b, and c are integers, then
a(b + c) = ab + ac and (b + c)a = ba + ca.
In either case, you distribute a times each term of the sum.
“Like terms” can be combined and simplified. The tool used for combining like terms is the distributive property. For example, consider the expression 3y + 7y, composed of two “like terms” with a common variable part. We can use the distributive property and write
Note that we are using the distributive property in reverse, “factoring out” the common variable part of each term. Checking our work, note that if we redistribute the variable part y times each term in the parentheses, we are returned to the original expression 3y + 7y.
Example 4
Use the distributive property to combine like terms (if possible) in each of the following expressions: (a) −5x2 − 9x2, (b) −5ab + 7ab, (c) 4y3 − 7y2, and (d) 3xy2 − 7xy2.
Solution
If the terms are “like terms,” you can use the distributive property to “factor out” the common variable part.
a) Factor out the common variable part x2.
b) Factor out the common variable part ab.
c) The terms in the expression 4y3 − 7y2 have different variable parts (the exponents are different). These are “unlike terms” and cannot be combined.
d) Factor out the common variable part xy2.
Exercise
Simplify: −8z − 11z
- Answer
-
−19z
Speeding Things Up a Bit
Once you’ve written out all the steps for combining like terms, like those shown in Example 4, you can speed things up a bit by following this rule:
Combining Like Terms
To combine like terms, simply add their coefficients and keep the common variable part.
Thus for example, when presented with the sum of two like terms, such as in 5x+ 8x, simply add the coefficients and repeat the common variable part; that is, 5x + 8x = 13x.
Example 5
Combine like terms:
- −9y − 8y,
- −3y5 + 4y5 and
- −3u2 + 2u2.
Solution
a) Add the coefficients and repeat the common variable part. Therefore,
b) Add the coefficients and repeat the common variable part. Therefore,
However, note that 1y5 = y5. Following the rule that the final answer should use as few symbols as possible, a better answer is −3y5 + 4y5 = y5.
c) Add the coefficients and repeat the common variable part. Therefore,
However, note that (−1)u2 = −u2. Following the rule that the final answer should use as few symbols as possible, a better answer is −3u2+ 2u2 = −u2.
Exercise
Combine: −3x, and − 4x2
- Answer
-
−7x2
Simplify
A frequently occurring instruction asks the reader to simplify an expression.
Simplify
The instruction simplify is a generic term that means “try to write the expression in its most compact form, using the fewest symbols possible.”
One way you can accomplish this goal is by combining like terms when they are present.
Example 6
Simplify: 2x + 3y − 5x + 8y.
Solution
Use the commutative property to reorder terms and the associative and distributive properties to regroup and combine like terms.
Alternate solution
Of course, you do not need to show the regrouping step. If you are more comfortable combining like terms in your head, you are free to present your work as follows:
Exercise
Simplify: −3a + 4b − 7a − 9b
- Answer
-
−10a − 5b
Example 7
Simplify: −2x − 3 − (3x + 4).
Solution
First, distribute the negative sign.
Next, use the commutative property to reorder, then the associative property to regroup. Then combine like terms.
Alternate solution
You may skip the second step if you wish, simply combining like terms mentally. That is, it is entirely possible to order your work as follows:
Exercise
Simplify: −9a − 4 − (4a − 8)
- Answer
-
−13a + 4
Example 8
Simplify: 2(5 − 3x) − 4(x + 3).
Solution
Use the distributive property to expand, then use the commutative and associative properties to group the like terms and combine them.
\[ \begin{aligned} 2(5-3x)-4(x+3) = 10-6x-4x-12 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \ =(-6x-4x)+(10-12) ~ & \textcolor{red}{ \text{ Group like terms.}} \ =-10x-2 ~ & \textcolor{red}{ \text{ Combine like terms: }} \ ~ & \textcolor{red}{-6x-4x=-10x \text{ and} \ ~ & \textcolor{red}{10-12=-2.} \end{aligned}\nonumber \]
Alternate solution
You may skip the second step if you wish, simply combining like terms mentally. That is, it is entirely possible to order your work as follows:
Exercise
Simplify: −2(3a − 4) − 2(5 − a)
- Answer
-
−4a − 2
Example 9
Simplify: −8(3x2y − 9xy) − 8(−7x2 − 8xy)
Solution
We will proceed a bit quicker with this solution, using the distributive property to expand, then combining like terms mentally.
Exercise
Simplify: (a2 − 2ab) − 2(3ab + a2)
- Answer
-
−a2 − 8ab
Applications
We can simplify a number of useful formulas by combining like terms.
Example 10
Find the perimeter P of the (a) rectangle and (b) square pictured below. Simplify your answer as much as possible.
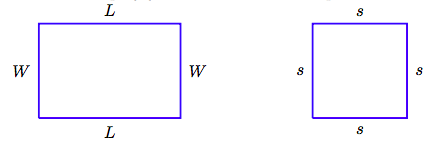
Solution
The perimeter of any polygonal figure is the sum of the lengths of its sides.
a) To find the perimeter P of the rectangle, sum its four sides.
Combine like terms.
b) To find the perimeter P of the square, sum its four sides.
Combine like terms.
Exercise
A regular hexagon has six equal sides, each with length x. Find its perimeter in terms of x.
- Answer
-
P = 6x
Sometimes it is useful to replace a variable with an expression containing another variable.
Example 11
The length of a rectangle is three feet longer than twice its width. Find the perimeter P of the rectangle in terms of its width alone.
Solution
From the previous problem, the perimeter of the rectangle is given by
where L and W are the length and width of the rectangle, respectively. This equation gives the perimeter in terms of its length and width, but we’re asked to get the perimeter in terms of the width alone. However, we’re also given the fact that the length is three feet longer than twice the width.
Because L = 3+2W, we can replace L with 3+2W in the perimeter equation 3.1.
Use the distributive property, then combine like terms.
This last equation gives the perimeter P in terms of the width W alone.
Exercise
The length L of a rectangle is 5 meters longer than twice its width W. Find the perimeter P of the rectangle in terms of its width W.
- Answer
-
Answer: P = 6W + 10
Example 12
The width of a rectangle is two feet less than its length. Find the perimeter P of the rectangle in terms of its length alone.
Solution
Again, the perimeter of a rectangle is given by the equation
where L and W are the length and width of the rectangle, respectively. This equation gives the perimeter in terms of its length and width, but we’re asked to get the perimeter in terms of the length alone.
However, we’re also given the fact that the width is two feet less than the length.
Because W = L−2, we can replace W with L−2 in the perimeter equation 3.2.
Use the distributive property, then combine like terms.
This last equation gives the perimeter P in terms of the length L alone.
Exercise
The width W of a rectangle is 5 feet less than twice its width L. Find the perimeter P of the rectangle in terms of its length L.
- Answer
-
P = 6L − 10
Exercises
In Exercises 1-16, combine like terms by first using the distributive property to factor out the common variable part, and then simplifying.
1. 17xy2 + 18xy2 + 20xy2
2. 13xy − 3xy + xy
3. −8xy2 − 3xy2 − 10xy2
4. −12xy − 2xy + 10xy
5. 4xy − 20xy
6. −7y3 + 15y3
7. 12r − 12r
8. 16s − 5s
9. −11x − 13x + 8x
10. −9r − 10r + 3r
11. −5q + 7q
12. 17n + 15n
13. r − 13r − 7r
14. 19m + m + 15m
15. 3x3 − 18x3
16. 13x2y + 2x2y
In Exercises 17-32, combine like terms by first rearranging the terms, then using the distributive property to factor out the common variable part, and then simplifying.
17. −8 + 17n + 10 + 8n
18. 11 + 16s − 14 − 6s
19. −2x3 − 19x2y − 15x2y + 11x3
20. −9x2y − 10y3 − 10y3 + 17x2y
21. −14xy − 2x3 − 2x3 − 4xy
22. −4x3 + 12xy + 4xy − 12x3
23. −13 + 16m + m + 16
24. 9 − 11x − 8x + 15
25. −14x2y − 2xy2 + 8x2y + 18xy2
26. −19y2 + 18y3 − 5y2 − 17y3
27. −14x3 + 16xy + 5x3 + 8xy
28. −16xy + 16y2 + 7xy + 17y2
29. 9n + 10 + 7 + 15n
30. −12r + 5 + 17 + 17r
31. 3y +1+6y + 3
32. 19p +6+8p + 13
In Exercises 33-56, simplify the expression by first using the distributive property to expand the expression, and then rearranging and combining like terms mentally.
33. −4(9x2y + 8) + 6(10x2y − 6)
34. −4(−4xy + 5y3) + 6(−5xy − 9y3)
35. 3(−4x2 + 10y2) + 10(4y2 − x2)
36. −7(−7x3 + 6x2) − 7(−10x2 − 7x3)
37. −s + 7 − (−1 − 3s)
38. 10y − 6 − (−10 − 10y)
39. −10q − 10 − (−3q + 5)
40. −2n + 10 − (7n − 1)
41. 7(8y + 7) − 6(8 − 7y)
42. −6(−5n − 4) − 9(3 + 4n)
43. 7(10x2 − 8xy2) − 7(9xy2 + 9x2)
44. 10(8x2y − 10xy2) + 3(8xy2 + 2x2y)
45. −2(6 + 4n) + 4(−n − 7)
46. −6(−2 − 6m) + 5(−9m + 7)
47. 8 − (4 + 8y)
48. −1 − (8 + s)
49. −8(−n + 4) − 10(−4n + 3)
50. 3(8r − 7) − 3(2r − 2)
51. −5 − (10p + 5)
52. −1 − (2p − 8)
53. 7(1 + 7r) + 2(4 − 5r)
54. (5 − s) + 10(9 + 5s)
55. −2(−5 − 8x2) − 6(6)
56. 8(10y2 + 3x3) − 5(−7y2 − 7x3)
57. The length L of a rectangle is 2 feet longer than 6 times its width W. Find the perimeter of the rectangle in terms of its width alone.
58. The length L of a rectangle is 7 feet longer than 6 times its width W. Find the perimeter of the rectangle in terms of its width alone.
59. The width W of a rectangle is 8 feet shorter than its length L. Find the perimeter of the rectangle in terms of its length alone.
60. The width W of a rectangle is 9 feet shorter than its length L. Find the perimeter of the rectangle in terms of its length alone.
61. The length L of a rectangle is 9 feet shorter than 4 times its width W. Find the perimeter of the rectangle in terms of its width alone.
62. The length L of a rectangle is 2 feet shorter than 6 times its width W. Find the perimeter of the rectangle in terms of its width alone.
Answers
1. 55xy2
3. −21xy2
5. −16xy
7. 0
9. −16x
11. 2q
13. −19r
15. −15x3
17. 2 + 25n
19. 9x3 − 34x2y
21. −18xy − 4x3
23. 3 + 17m
25. −6x2y + 16xy2
27. −9x3 + 24xy
29. 24n + 17
31. 9y + 4
33. 24x2y − 68
35. −22x2 + 70y2
37. 2s + 8
39. −7q − 15
41. 98y + 1
43. 7x2 − 119xy2
45. −40 − 12n
47. 4 − 8y
49. 48n − 62
51. −10 − 10p
53. 15 + 39r
55. −26 + 16x2
57. 4 + 14W
59. 4L − 16
61. 10W − 18


