1.5: Solve Linear Inequalities

Last updated
Save as PDF

Page ID: 109045

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Graph inequalities on the number line
Solve linear inequalities
Translate words to an inequality and solve
Solve applications with linear inequalities

Warm-up

Solve

$x+3=5$
$-x+3=5$
$-2x-3=-9$

Solution

2
-2
3

Graph Inequalities on the Number Line

What number would make the inequality $x>3$ true? Are you thinking, "$x$ could be four"? That’s correct, but $x$ could be 6, too, or 37, or even 3.001. Any number greater than three is a solution to the inequality $x>3$. We show all the solutions to the inequality $x>3$ on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can also represent inequalities using interval notation. There is no upper end to the solution to this inequality. In interval notation, we express $x>3$ as $(3,\infty)$. The symbol $\infty$ is read as “infinity.” It is not an actual number. Figure $\PageIndex{1}$ shows both the number line and the interval notation.

The figure shows the inquality, x is greater than 3, graphed on a number line from negative 5 to 5. There is shading that starts at 3 and extends to numbers to its right. The solution for the inequality is written in interval notation. It is the interval from 3 to infinity, not including 3. — Figure $\PageIndex{1}$: The inequality $x>3$ is graphed on this number line and written in interval notation.

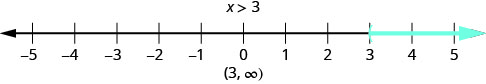
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, shows that the endpoint is included.

The inequality $x\leq 1$ means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at $x=1$. We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure $\PageIndex{2}$). There is no lower end to those numbers. We write $x\leq 1 $in interval notation as $(−\infty,1]$. The symbol $−\infty$ is read as “negative infinity.”

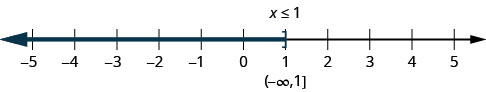
The figure shows the inquality, x is less than or equal to l, graphed on a number line from negative 5 to 5. There is shading that starts at 1 and extends to numbers to its left. The solution for the inequality is written in interval notation. It is the interval from negative infinity to one, including 1. — Figure $\PageIndex{2}$: The inequality $x\leq 1$ is graphed on this number line and written in interval notation.

Figure $\PageIndex{3}$ shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

$The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.$

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.

Example $\PageIndex{1}$

Graph each inequality on the number line and write in interval notation.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Answer

ⓐ

Solution to a.
	$ x \geq -3 $
Shade to the right of $−3$, and put a bracket at $−3$.	$.$
Write in interval notation.	$ [-3, \infty) $

ⓑ

Solution to b.
	$ x < 2.5 $
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	$ (-\infty, 2.5) $

ⓒ

Solution to c.
	$ x \leq -\dfrac{3}{5} $
Shade to the left of $−\frac{3}{5}$, and put a bracket at $−\frac{3}{5}$.	$.$
Write in interval notation.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

Graph each inequality on the number line and write in interval notation:

$x>2$
$x\leq −1.5$
$x\geq \frac{3}{4}$.

Answer

ⓐ

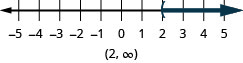
$The graph of the inequality x is greater than 2 is indicated on a number line with a left parenthesis at 2 and shading to the right. The solution in interval notation is the interval from 2 to infinity enclosed within parentheses.$

ⓑ

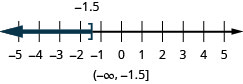
$The graph of the inequality x is less than or equal to negative 1.5 is indicated on a number line with a right bracket at negative 1.5 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 1.5 enclosed within a left parenthesis and right bracket.$

ⓒ

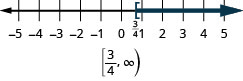
$The graph of the inequality x is greater than or rqual to three-fourths is indicated on a number line with a left bracket at three-fourths and shading to the right. The solution in interval notation is the interval from three-fourths to infinity enclosed within a left bracket and left parentheses.$

Example $\PageIndex{3}$

Graph each inequality on the number line and write in interval notation:

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$.

Answer

ⓐ

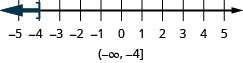
$The graph of the inequality x is less than or equal to negative 4 is indicated on a number line with a right bracket at negative 4 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 4 enclosed within an left parenthesis and right bracket.$

ⓑ

$The graph of the inequality x is greater than or equal to 0.5 is indicated on a number line with a left bracket at 0.5 and shading to the right. The solution in interval notation is the interval from 0.5 to infinity enclosed within a left bracket and right parenthesis.$

ⓒ

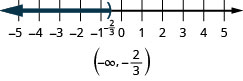
$The graph of the inequality x is less than negative two-thirds is indicated on a number line with a right parenthesis at negative two-thirds and shading to the left. The solution in interval notation is the interval from negative infinity to negative two-thirds enclosed within parentheses.$

What numbers are greater than two but less than five? Are you thinking say, $2.5,\space 3,\space 3\frac{2}{3},\space 4$? We can represent all the numbers between two and five with the inequality $2<x<5$. We can show $2<x<5$ on the number line by shading all the numbers between two and five. Again, we use the parentheses to show the numbers two and five are not included. See Figure.

The graph of the inequality 2 is less than x which is less than 5 shows open circles a 2 and 5 and shading in between. — Figure $\PageIndex{3}$

Graph each inequality on the number line and write in interval notation.

ⓐ $−3<x<4$ ⓑ $−6\leq x<−1$ ⓒ $0\leq x\leq 2.5$

Answer

ⓐ

Solution to a.
		$-3 < x < 4$
Shade between $−3$ and 4. Put a parentheses at $−3$ and 4.		$.$
Write in interval notation.		$ (-3,4) $

ⓑ

Solution to b.
			$ -6 \leq x < -1 $
Shade between $−6$ and −1. Put a bracket at $−6$, and a parenthesis at −1.			$.$
Write in interval notation.			$ [-6,1) $

ⓒ

Solution to c.
			$ 0 \leq x \leq 2.5 $
Shade between 0 and 2.5. Put a bracket at 0 and at 2.5.			$.$
Write in interval notation.			$ [0, 2.5] $

Example $\PageIndex{5}$

Graph each inequality on the number line and write in interval notation:

ⓐ $−2<x<1$ ⓑ $−5\leq x<−4$ ⓒ $1\leq x\leq 4.25$

Answer

ⓐ

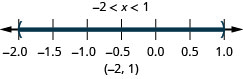
$Negative 2 is less x which is less than 1. There are open circles at negative 2 and 1 and shading between negative 2 and 1 on the number line. Put parentheses at negative 2 and 1. Write in interval notation.$

ⓑ

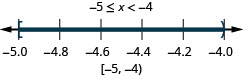
$Negative 5 is less than or equal to x which is less than negative 4. There is a closed circle at negative 6 and an open circle at negative 4 and shading between negative 5 and negative 4 on the number line. Put a bracket at negative 5 and a parenthesis at negative 4. Write in interval notation.$

ⓒ

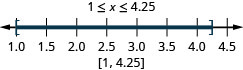
$1 is less than or equal to x which is less than 4.25. There is closed circle at 1 and a closed circle at 4.25 and shading between 1 and 4.25 on the number line. Put brackets at 1 and 4.25. Write in interval notation.$

Example $\PageIndex{6}$

Graph each inequality on the number line and write in interval notation:

ⓐ $−6<x<2$ ⓑ $−3\leq x< −1$ ⓒ $2.5\leq x\leq 6$

Answer

ⓐ

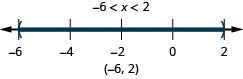
$Negative 6 is less than x which is less than 2. There is an open circle at negative 6 and an open circle at 2 and shading between negative 6 and 2 on the number line. Put parentheses at negative 6 and 2. Write in interval notation.$

ⓑ

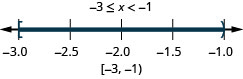
$Negative 3 is less than or equal to x which is less than negative 1. There is a closed circle at negative 3 and an open circle at negative 1 and shading between negative 3 and negative 1 on the number line. Put a bracket at negative 3 and a parenthesis at negative 1. Write in interval notation.$

ⓒ

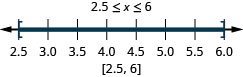
$2.5 is less than or equal to x which is less thanor equal to 6. There is a closed circle at 2.5 and a closed circle at 6 and shading between 2.5 and 6 on the number line. Put brackets at 2.5 and 6. Write in interval notation.$

Solve Linear Inequalities

A linear inequality is much like a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that can be written in one of the forms, $ax+b<c$, $ax+b\leq c$, $ax+b>c$, or $ax+b\geq c$.

Definition: LINEARE INEQUALITY

A linear inequality is an inequality in one variable that can be written in one of the following forms where $a, \, b,$ and $c$ are real numbers and $a≠0$:

\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still keep the equality. Similar properties hold true for inequalities.

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality. For example:

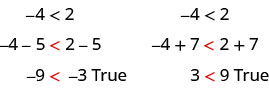
$Negative 4 is less than 2. Negative 4 minus 5 is less than 2 minus 5. Negative 9 is less than negative 3, which is true. Negative 4 is less than 2. Negative 4 plus 7 is less than 2 plus 7. 3 is less than 9, which is true.$

Notice that the inequality sign stayed the same.

This leads us to the Addition and Subtraction Properties of Inequality.

Definition: ADDITION AND SUBTRACTION PROPERTY OF INEQUALITY

For any numbers $a, \, b,$ and $c,$ if $a<b$, then

\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality

What happens to an inequality when we divide or multiply both sides by a constant?

Let’s first multiply and divide both sides by a positive number.

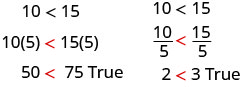
$10 is less than 15. 10 times 5 is less than 15 times 5. 50 is less than 75 is true. 10 is less than 15. 10 divided by 5 is less than 15 divided by 5. 2 is less than 3 is true.$

The inequality signs stayed the same.

Does the inequality stay the same when we divide or multiply by a negative number?

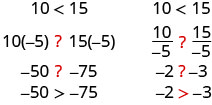
$10 is less than 15 10 times negative 5 is blank 15 times negative 5? Negative 50 is blank negative 75. Negative 50 is greater than negative 75. 10 is less than 15. 10 divided by negative 5 is blank 15 divided by negative 5. Negative 2 is blank negative 3. Negative 2 is blank negative 3.$

Notice that when we filled in the inequality signs, the inequality signs reversed their direction.

When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.

This gives us the Multiplication and Division Property of Inequality.

Definition: MULTIPLICATION AND DIVISION PROPERTY OF INEQUALITY

For any numbers $a, \, b,$ and $c,$

\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

When we divide or multiply an inequality by $a$:

positive number, the inequality stays the same.
negative number, the inequality reverses.

Sometimes when solving an inequality, as in the next example, the variable ends upon the right. We can rewrite the inequality in reverse to get the variable to the left.

\[x>a \text{ has the same meaning as } a<x \nonumber \]

Think about it as “If Xander is taller than Andy, then Andy is shorter than Xander.”

Example $\PageIndex{7}$

Solve each inequality. Graph the solution on the number line, and write the solution in interval notation.

ⓐ $x−\frac{3}{8}\leq \frac{3}{4}$ ⓑ $9y<54$ ⓒ $−15<\frac{3}{5}z$

Answer

ⓐ

Solution to a.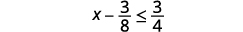
	$.$
Add 3838 to both sides of the inequality.	$.$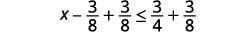
Simplify.	$.$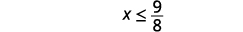
Graph the solution on the number line.	$.$
Write the solution in interval notation.	$.$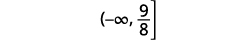

ⓑ

Solution to b.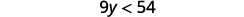
	$.$
Divide both sides of the inequality by 9; since 9 is positive, the inequality stays the same.	$.$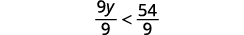
Simplify.	$.$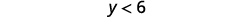
Graph the solution on the number line.	$.$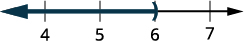
Write the solution in interval notation.	$.$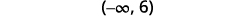

ⓒ

Solution to c.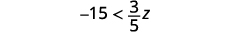
	$.$
Multiply both sides of the inequality by $\frac{5}{3}$. Since $\frac{5}{3}$ is positive, the inequality stays the same.	$.$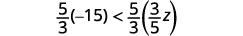
Simplify.	$.$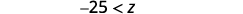
Rewrite with the variable on the left.	$.$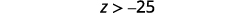
Graph the solution on the number line.	$.$
Write the solution in interval notation.	$.$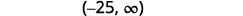

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $p−\frac{3}{4}\geq \frac{1}{6}$ ⓑ $9c>72$ ⓒ $24\leq \frac{3}{8}m$

Answer

ⓐ

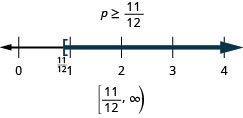
$p is less than eleven-twelfths. The solution on the number line has a right bracket at eleven-twelfths with shading to the right. The solution in interval notation is, eleven-twelfths to infinity within a bracket and parenthesis.$

ⓑ

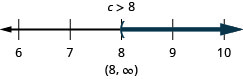
$c is less than 8. The solution on the number line has a left bracket at 8 with shading to the right. The solution in interval notation is, 8 to infinity within parentheses.$

ⓒ

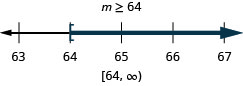
$m is greater than or equal to 8. The solution on the number line has a right bracket at 64 with shading to the right. The solution in interval notation is, 64 to infinity within a bracket and parentheses.$

Example $\PageIndex{9}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $r−\frac{1}{3}\leq \frac{7}{12}$ ⓑ $12d\leq 60$ ⓒ $−24<\frac{4}{3}n$

Answer

ⓐ

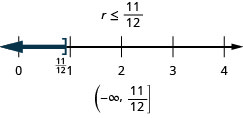
$r is less than or equal to eleven-twelfths. The solution on the number line has a left bracket at eleven-twelfths with shading to the left. The solution in interval notation is negative infinity to eleven-twelfths within a parenthesis and a bracket.$

ⓑ

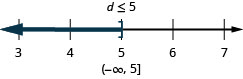
$c is less than or equal to 5. The solution on the number line has a right bracket at 5 with shading to the left. The solution in interval notation is negative infinity to 5 within a parentheses and a bracket.$

ⓒ

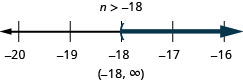
$n is greater than negative 18. The solution on the number line has a left parenthesis at negative 18 with shading to the right. The solution in interval notation is negative 18 to infinity within parentheses.$

Be careful when you multiply or divide by a negative number—remember to reverse the inequality sign.

Example $\PageIndex{10}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation.

ⓐ $−\frac{1}{3}m\geq \frac{6}{5}$ ⓑ $\frac{n}{−2} \geq 8$

Answer

ⓐ

Solution to a.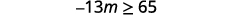
	$.$
Divide both sides of the inequality by $−\frac{1}{3}$. Since $−\frac{1}{3}$ is a negative, the inequality reverses.	$.$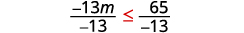
Simplify.	$.$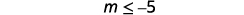
Graph the solution on the number line.	$.$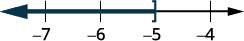
Write the solution in interval notation.	$.$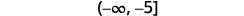

ⓑ

Solution to b.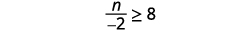
	$.$
Multiply both sides of the inequality by $−2$. Since $−2$ is a negative, the inequality reverses.	$.$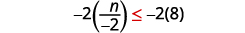
Simplify.	$.$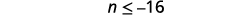
Graph the solution on the number line.	$.$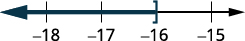
Write the solution in interval notation.	$.$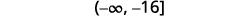

Example $\PageIndex{11}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $−8q<32$ ⓑ $\frac{k}{−12} \leq 15$.

Answer

ⓐ

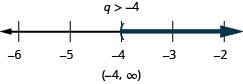
$q is greater than or equal to negative 4. The solution on the number line has a left parenthesis at negative 4 with shading to the right. The solution in interval notation is negative 4 to infinity within parentheses.$

ⓑ

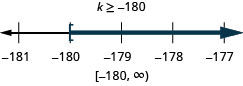
$k is greater than or equal to negative 180. The solution on the number line has a left bracket at negative 180 with shading to the right. The solution in interval notation is negative 180 to infinity within a bracket and a parenthesis.$

Example $\PageIndex{12}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $−7r\leq −70$ ⓑ $\frac{u}{−4}\geq −16$.

Answer

ⓐ

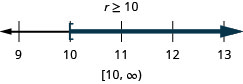
$r is greater than or equal to 10. The solution on the number line has a left bracket at 10 with shading to the right. The solution in interval notation is 10 to infinity within a bracket and parenthesis.$

ⓑ

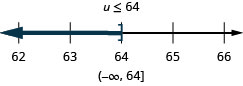
$u is less than or equal to 64. The solution on the number line has a right bracket at 64 with shading to the left. The solution in interval notation is negative infinity to 64 within parenthesis and a bracket.$

Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but make sure to pay close attention when we multiply or divide to isolate the variable.

Example $\PageIndex{13}$

Solve the inequality $6y\leq 11y+17$, graph the solution on the number line, and write the solution in interval notation.

Solution

Solution to the example.
	$.$
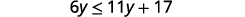Subtract 11y from both sides to collect the variables on the left.	$.$
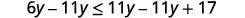Simplify.	$.$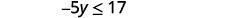
Divide both sides of the inequality by −5, and reverse the inequality.	$.$
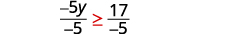Simplify.	$.$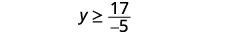
Graph the solution on the number line.	$.$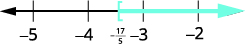
Write the solution in interval notation.	$.$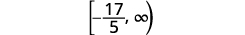

Exercise $\PageIndex{14}$

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: $3q\geq 7q−23$.

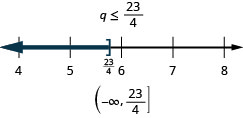
Answer: $q is less than or equal to 23 divided by 4. The solution on the number line has a right bracket at 23 divided by 4 with shading to the left. The solution in interval notation is negative infinity to 23 divided by 4 within a parenthesis and a bracket.$

Example $\PageIndex{15}$

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: $6x<10x+19$.

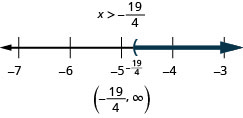
Answer: $x is greater than negative 19 divided by 4. The solution on the number line has a left parenthesis at negative 19 divided by 4 with shading to the right. The solution in interval notation is negative 19 divided by 4 to infinity within parentheses.$

When solving inequalities, it is usually easiest to collect the variables on the side where the coefficient of the variable is largest. This eliminates negative coefficients and so we don’t have to multiply or divide by a negative—which means we don’t have to remember to reverse the inequality sign.

Example $\PageIndex{16}$

Solve the inequality $8p+3(p−12)>7p−28$, graph the solution on the number line, and write the solution in interval notation.

Answer

Solution to the example.
	$8p+3(p−12)>7p−28$
Simplify each side as much as possible.
Distribute.	$8p+3p−36>7p−28$
Combine like terms.	$11p−36>7p−28$
Subtract $7p$ from both sides to collect the variables on the left, since $11>7$.	$11p−36−7p>7p−28−7p$
Simplify.	$4p−36>−28$
Add $36$ to both sides to collect the constants on the right.	$4p−36+36>−28+36$
Simplify.	$4p>8$
Divide both sides of the inequality by $4$; the inequality stays the same.	$\dfrac{4p}{4}>\dfrac{8}{4}$
Simplify.	$p>2$
Graph the solution on the number line.	$.$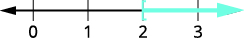
Write the solution in interval notation.	$(2,\infty)$

Example $\PageIndex{17}$

Solve the inequality $9y+2(y+6)>5y−24$, graph the solution on the number line, and write the solution in interval notation.

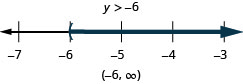
Answer: $y is greater than negative 6. The solution on the number line has a left parenthesis at negative 6 with shading to the right. The solution in interval notation is negative 6 to infinity within parentheses.$

Example $\PageIndex{18}$

Solve the inequality $6u+8(u−1)>10u+32$, graph the solution on the number line, and write the solution in interval notation.

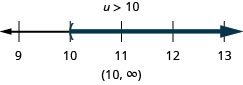
Answer: $u is greater than negative 10. The solution on the number line has a left parenthesis at 10 with shading to the right. The solution in interval notation is 10 to infinity within parentheses.$

Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.

Example $\PageIndex{19}$

Solve the inequality $8x−2(5−x)<4(x+9)+6x$, graph the solution on the number line, and write the solution in interval notation.

Answer

Solution to the example.
Simplify each side as much as possible.		$8x−2(5−x)<4(x+9)+6x$
Distribute.		$8x−10+2x<4x+36+6x$
Combine like terms.		$10x−10<10x+36$
Subtract ${\color{red}{10x}}$ from both sides to collect the variables on the left.		$10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}$
Simplify.		$−10<36$
The $x$'s are gone, and we have a true statement.		The inequality is an identity. The solution is all real numbers.
Graph the solution on the number line.		$.$
Write the solution in interval notation.		$(−\infty,\infty)$

Example $\PageIndex{20}$

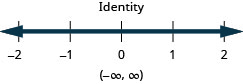
Solve the inequality $4b−3(3−b)>5(b−6)+2b$, graph the solution on the number line, and write the solution in interval notation.

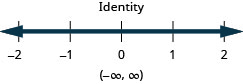
Answer: $The inequality is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

Example $\PageIndex{21}$

Solve the inequality $9h−7(2−h)<8(h+11)+8h$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

We can clear fractions in inequalities much as we did in equations. Again, be careful with the signs when multiplying or dividing by a negative.

Example $\PageIndex{22}$

Solve the inequality $\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$, graph the solution on the number line, and write the solution in interval notation.

Answer

Solution to the example.
	$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$
Multiply both sides by the LCD, 24, to clear the fractions.	${\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)$
Simplify.	$ 8a - 3a > 5a + 18 $
Combine like terms.	$ 5a > 5a + 18$
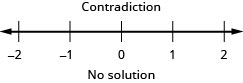
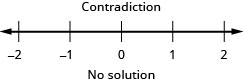
Subtract $5a$ from both sides to collect the variables on the left.	$ 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18$
Simplify.	$0 > 18 $
The statement is false.	The inequality is a contradiction. There is no solution.
Graph the solution on the number line.	$.$
Write the solution in interval notation.	There is no solution.

Example $\PageIndex{23}$

Solve the inequality $\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.$

Example $\PageIndex{24}$

Solve the inequality $\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.$

Key Concepts

Inequalities, Number Lines, and Interval Notation
$x>a \quad x\geq a\quad x<a\quad x\leq a$
$The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.$
Linear Inequality
- A linear inequality is an inequality in one variable that can be written in one of the following forms where a, b, and care real numbers and $a\neq 0$:
  \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
Addition and Subtraction Property of Inequality
- For any numbers a, b, and c, if a<b,thena<b,then
  \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- We can add or subtract the same quantity from both sides of an inequality and still keep the inequality.
Multiplication and Division Property of Inequality
- For any numbers a, b, and c,
  $\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}$

	\( x \geq -3 \)
Shade to the right of \(−3\), and put a bracket at \(−3\).	$.$
Write in interval notation.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Shade to the left of \(−\frac{3}{5}\), and put a bracket at \(−\frac{3}{5}\).	$.$
Write in interval notation.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

		\(-3 < x < 4\)
Shade between \(−3\) and 4. Put a parentheses at \(−3\) and 4.		$.$
Write in interval notation.		\( (-3,4) \)

			\( -6 \leq x < -1 \)
Shade between \(−6\) and −1. Put a bracket at \(−6\), and a parenthesis at −1.			$.$
Write in interval notation.			\( [-6,1) \)

	\(8p+3(p−12)>7p−28\)
Simplify each side as much as possible.
Distribute.	\(8p+3p−36>7p−28\)
Combine like terms.	\(11p−36>7p−28\)
Subtract \(7p\) from both sides to collect the variables on the left, since \(11>7\).	\(11p−36−7p>7p−28−7p\)
Simplify.	\(4p−36>−28\)
Add \(36\) to both sides to collect the constants on the right.	\(4p−36+36>−28+36\)
Simplify.	\(4p>8\)
Divide both sides of the inequality by \(4\); the inequality stays the same.	\(\dfrac{4p}{4}>\dfrac{8}{4}\)
Simplify.	\(p>2\)
Graph the solution on the number line.	$.$
Write the solution in interval notation.	\((2,\infty)\)

Search

Solution

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

Example \(\PageIndex{1}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Definition: LINEARE INEQUALITY

Definition: ADDITION AND SUBTRACTION PROPERTY OF INEQUALITY

Definition: MULTIPLICATION AND DIVISION PROPERTY OF INEQUALITY

Example \(\PageIndex{7}\)

Example \(\PageIndex{9}\)

Example \(\PageIndex{10}\)

Example \(\PageIndex{11}\)

Example \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Solution

Exercise \(\PageIndex{14}\)

Example \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Example \(\PageIndex{17}\)

Example \(\PageIndex{18}\)

Example \(\PageIndex{19}\)

Example \(\PageIndex{20}\)

Example \(\PageIndex{21}\)

Example \(\PageIndex{22}\)

Example \(\PageIndex{23}\)

Example \(\PageIndex{24}\)

	\( x < 2.5 \)
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	\( (-\infty, 2.5) \)

			\( 0 \leq x \leq 2.5 \)
Shade between 0 and 2.5. Put a bracket at 0 and at 2.5.			$.$
Write in interval notation.			\( [0, 2.5] \)

	$.$
Divide both sides of the inequality by \(−\frac{1}{3}\). Since \(−\frac{1}{3}\) is a negative, the inequality reverses.	$.$
Simplify.	$.$
Graph the solution on the number line.	$.$
Write the solution in interval notation.	$.$

Simplify each side as much as possible.		\(8x−2(5−x)<4(x+9)+6x\)
Distribute.		\(8x−10+2x<4x+36+6x\)
Combine like terms.		\(10x−10<10x+36\)
Subtract \({\color{red}{10x}}\) from both sides to collect the variables on the left.		\(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
Simplify.		\(−10<36\)
The \(x\)'s are gone, and we have a true statement.		The inequality is an identity. The solution is all real numbers.
Graph the solution on the number line.		$.$
Write the solution in interval notation.		\((−\infty,\infty)\)

	\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
Multiply both sides by the LCD, 24, to clear the fractions.	\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
Simplify.	\( 8a - 3a > 5a + 18 \)
Combine like terms.	\( 5a > 5a + 18\)
Subtract \(5a\) from both sides to collect the variables on the left.	\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
Simplify.	\(0 > 18 \)
The statement is false.	The inequality is a contradiction. There is no solution.
Graph the solution on the number line.	$.$
Write the solution in interval notation.	There is no solution.