3.1: Use a General Strategy to Solve Linear Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Solve linear equations with integer coefficients
- Solve linear equations with fraction and decimal coefficients
- Determine whether the values are solutions to the equation: 6x−2=4x+8.
- x=5
- x=2
- Solve for x: 3x−4+6x=22
- Find the LCD of 56 and 14.
- Answer
-
- For the equation 6x−2=4x+8
- x=5 is a solution
- x=2 is not a solution
- x=2
- 12
- For the equation 6x−2=4x+8
Solve Linear Equations Using a General Strategy
In the first chapter, we did a quick introduction to the basics of solving equations. Before diving into the world of linear functions (as well as other kinds of functions) in depth, it is worth revisiting these skills and discussing a general strategy we can use to solve equations. This section will be a little shorter than usual because we've already covered (and used!) some of the necessary skills already; it's just time to bring them all together so we can solve more complicated problems!
There are many types of equations that we will learn to solve. In this section we will focus on a linear equation. You've already worked with linear equations, so we are just formalizing some information we already have.
A linear equation is an equation in one variable that can be written, where a and b are real numbers and a≠0, as:
ax+b=0.
An easy way to think about linear equations is that these are the equations where the variable appears by itself, and has been multiplied by a constant or has a constant added to it, but there are no exponents attached to it, no absolute values, no square roots, etc. We will see later that these equations are closely related to the linear functions that we looked at in the last chapter.
To solve a linear equation it is a good idea to have an overall strategy that can be used to solve any linear equation. In the next example, we will give the steps of a general strategy for solving any linear equation. Simplifying each side of the equation as much as possible first makes the rest of the steps easier.
Solve: 7(n−3)−8=−15
- Answer
-




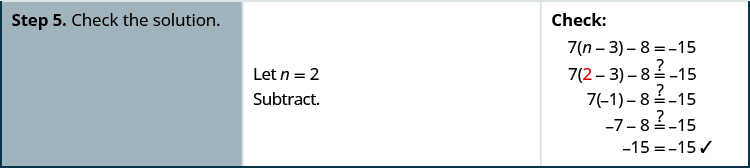
Solve: 2(m−4)+3=−1.
- Answer
-
m=2
Solve: 5(a−3)+5=−10.
- Answer
-
a=0
These steps are summarized in the General Strategy for Solving Linear Equations below.
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality.
- Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality.
- Make the coefficient of the variable term equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation.
- Check the solution.
Substitute the solution into the original equation to make sure the result is a true statement.
Solve: 23(3m−6)=5−m.
- Answer
-
23(3m−6)=5−m Distribute. 2m−4=5−m Add m to both sides to get the variables only on the left. 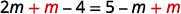
Simplify. 3m−4=5 Add 4 to both sides to get constants only on the right. 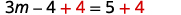
Simplify. 3m=9 Divide both sides by three. 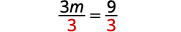
Simplify. m=3
| Check: | 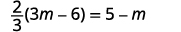 |
| Let m=3. | 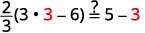 |
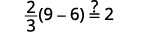 |
|
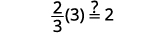 |
|
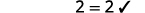 |
Solve: 13(6u+3)=7−u.
- Answer
-
u=2
Solve: 23(9x−12)=8+2x.
- Answer
-
x=4
We can solve equations by getting all the variable terms to either side of the equal sign. By collecting the variable terms on the side where the coefficient of the variable is larger, we avoid working with some negatives. This will be a good strategy when we solve inequalities later in this chapter. It also helps us prevent errors with negatives.
Solve: 4(x−1)−2=5(2x+3)+6.
- Answer
-
4(x−1)−2=5(2x+3)+6 Distribute. 4x−4−2=10x+15+6
Combine like terms. 4x−6=10x+21 Subtract 4x from each side to get the variables only on the right since 10>4. 4x−4x−6=10x−4x+21 Simplify. −6=6x+21 Subtract 21 from each side to get the constants on left. −6−21=6x+21−21
Simplify. −27=6x Divide both sides by 6. −276=6x6 Simplify. −92=x Check: 4(x−1)−2=5(2x+3)+6\) Let x=−92. 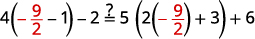
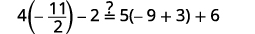
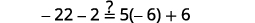
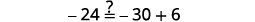
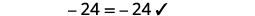
Solve: 6(p−3)−7=5(4p+3)−12.
- Answer
-
p=−2
Solve: 8(q+1)−5=3(2q−4)−1.
- Answer
-
q=−8
Solve: 10[3−8(2s−5)]=15(40−5s).
- Answer
-
10[3−8(2s−5)]=15(40−5s) Simplify from the innermost parentheses first. 10[3−16s+40]=15(40−5s) Combine like terms in the brackets. 10[43−16s]=15(40−5s) Distribute. 430−160s=600−75s Add 160s to both sides to get the 160s to both sides to get the variables to the right. 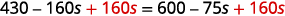
Simplify. 430=600+85s Subtract 600 from both sides to get the constants to the left. 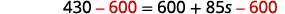
Simplify. −170=85s Divide both sides by 85. 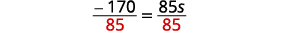
Simplify. −2=s, so s=−2 Check: 10[3−8(2s−5)]=15(40−5s) Let s=−2. 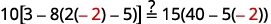
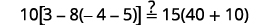
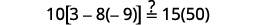
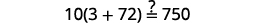
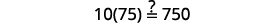
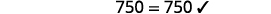
Solve: 6[4−2(7y−1)]=8(13−8y).
- Answer
-
y=−175
Solve: 12[1−5(4z−1)]=3(24+11z).
- Answer
-
z=0
Solve Equations with Fraction or Decimal Coefficients
We could use the General Strategy to solve the next example. This method would work fine, but working with the fractions can get a bit tedious, and also increases the number of opportunities for making a mistake. So, we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.
We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator (LCD) of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but without fractions. This process is called clearing the equation of fractions.
To clear an equation of decimals, we think of all the decimals in their fraction form and then find the LCD of those denominators.
Solve: 112x+56=34.
- Answer
-



Solve: 14x+12=58.
- Answer
-
x=12
Solve: 18x+12=14.
- Answer
-
x=−2
Notice in the previous example, once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve. We then used the General Strategy for Solving Linear Equations.
- Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
- Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
- Solve using the General Strategy for Solving Linear Equations.
Solve: 5=12y+23y−34y.
- Answer
-
We want to clear the fractions by multiplying both sides of the equation by the LCD of all the fractions in the equation.
Find the LCD of all fractions in the equation. 5=12y+23y−34y The LCD is 12. Multiply both sides of the equation by 12. 12(5)=12⋅(12y+23y−34y) Distribute. 12(5)=12⋅12y+12⋅23y−12⋅34y Simplify—notice, no more fractions. 60=6y+8y−9y Combine like terms. 60=5y Divide by five. 605=5y5 Simplify. 12=y Check: 5=12y+23y−34y Let y=12. 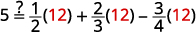
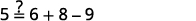

Solve: 7=12x+34x−23x.
- Answer
-
x=12
Solve: −1=12u+14u−23u.
- Answer
-
u=−12
In the next example, we’ll distribute before we clear the fractions.
Solve: 12(y−5)=14(y−1).
- Answer
-
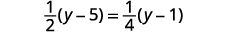
Distribute. 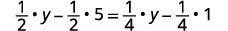
Simplify. 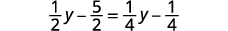
Multiply by the LCD, four. 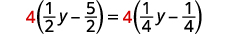
Distribute. 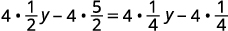
Simplify. 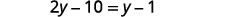
Collect the variables to the left. 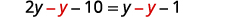
Simplify. 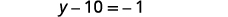
Collect the constants to the right. 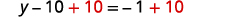
Simplify. 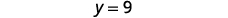
An alternate way to solve this equation is to clear the fractions without distributing first. If you multiply the factors correctly, this method will be easier. 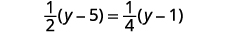
Multiply by the LCD, 4. 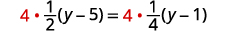
Multiply four times the fractions. 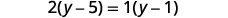
Distribute. 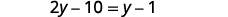
Collect the variables to the left. 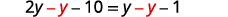.jpg?revision=1&size=bestfit&width=228&height=17)
Simplify. 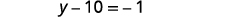
Collect the constants to the right. 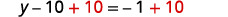
Simplify. 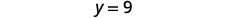
Check: 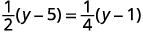
Let y=9. 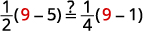
Finish the check on your own.
Solve: 15(n+3)=14(n+2).
- Answer
-
n=2
Solve: 12(m−3)=14(m−7).
- Answer
-
m=−1
When you multiply both sides of an equation by the LCD of the fractions, make sure you multiply each term by the LCD—even if it does not contain a fraction.
Solve: 4q+32+6=3q+54
- Answer
-
4q+32+6=3q+54 Multiply both sides by the LCD, 4. 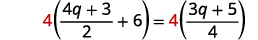
Distribute. 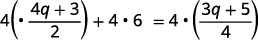
Simplify. 2(4q+3)+24=3q+5 8q+6+24=3q+5 8q+30=3q+5 Collect the variables to the left. 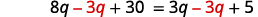
Simplify. 5q+30=5 Collect the constants to the right. 
Simplify. 5q=−25 Divide both sides by five. 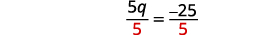
Simplify. q=−5 Check: 4q+32+6=3q+54 Let q=−5. 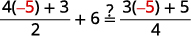
Finish the check on your own.
Solve: 2s+32+1=3s+24.
- Answer
-
s=−8
Solve: 3r+56+1=4r+33.
- Answer
-
r=3
Some equations have decimals in them. This kind of equation may occur when we solve problems dealing with money or percentages. But decimals can also be expressed as fractions. For example, 0.7=710 and 0.29=29100. So, with an equation with decimals, we can use the same method we used to clear fractions—multiply both sides of the equation by the least common denominator.
The next example uses an equation that is typical of the ones we will see in the money applications in a later section. Notice that we will clear all decimals by multiplying by the LCD of their fraction form.
Solve: 0.25x+0.05(x+3)=2.85.
- Answer
-
Look at the decimals and think of the equivalent fractions:
0.25=25100,0.05=5100,2.85=285100.
Notice, the LCD is 100. By multiplying by the LCD we will clear the decimals from the equation.
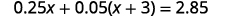
Distribute first. 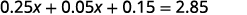
Combine like terms. 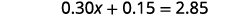
To clear decimals, multiply by 100. 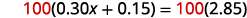
Distribute. 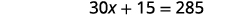
Subtract 15 from both sides. 
Simplify. 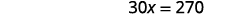
Divide by 30. 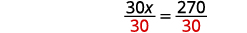
Simplify. 
Check it yourself by substituting x=9 into the original equation.
Solve: 0.25n+0.05(n+5)=2.95.
- Answer
-
n=9
Solve: 0.10d+0.05(d−5)=2.15.
- Answer
-
d=16
Key Concepts
- How to Solve Linear Equations Using a General Strategy
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms.
- Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality.
- Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality.
- Make the coefficient of the variable term equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation.
- Check the solution.
Substitute the solution into the original equation to make sure the result is a true statement.
- Simplify each side of the equation as much as possible.
- How to Solve Equations with Fraction or Decimal Coefficients
- Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
- Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
- Solve using the General Strategy for Solving Linear Equations.

