3.3: Slope Intercept Form
- Page ID
- 109443
By the end of this section, you will be able to:
- Find the slope of a line
- Graph a line given a point and the slope
- Graph a line using its slope and intercept
- Choose the most convenient method to graph a line
- Graph and interpret applications of slope–intercept
- Use slopes to identify parallel and perpendicular lines
- Simplify: \(\frac{1-4}{8-2}\)
- Divide: \(\frac{0}{4}\), \(\frac{4}{0}\).
- Simplify: \(\frac{15}{-3}\), \(\frac{-15}{3}\), \(\frac{-15}{-3}\).
- Answer
-
- -2
- 0, undefined
- -5, -5, 5
Find the Slope of a Line
When you graph linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter.
In mathematics, the measure of the steepness of a line is called the slope of the line.
The concept of slope has many applications in the real world. In construction the pitch of a roof, the slant of the plumbing pipes, and the steepness of the stairs are all applications of slope. and as you ski or jog down a hill, you definitely experience slope.
We can assign a numerical value to the slope of a line by finding the ratio of the rise and run. The rise is the amount the vertical distance changes while the run measures the horizontal change, as shown in this illustration. Slope is a rate of change.
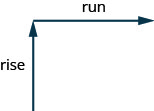
The slope of a line is \(m=\frac{\text{rise}}{\text{run}}\).
The rise measures the vertical change and the run measures the horizontal change.
To find the slope of a line, we locate two points on the line whose coordinates are integers. Then we sketch a right triangle where the two points are vertices and one side is horizontal and one side is vertical.
To find the slope of the line, we measure the distance along the vertical and horizontal sides of the triangle. The vertical distance is called the rise and the horizontal distance is called the run.
- Locate two points on the line whose coordinates are integers.
- Starting with one point, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope: \(m=\frac{\text{rise}}{\text{run}}\).
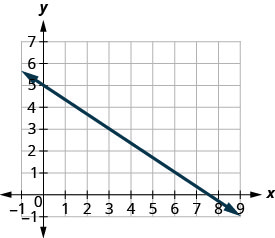
Find the slope of the line shown.
- Answer
-
Locate two points on the graph whose
coordinates are integers.\((0,5)\) and \((3,3)\) Starting at \((0,5)\), sketch a right triangle to
\((3,3)\) as shown in this graph.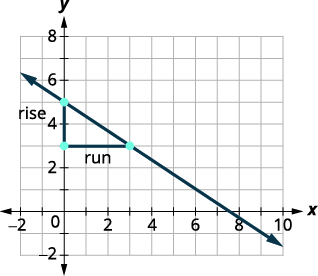
Count the rise— since it goes down, it is negative. The rise is \(−2\). Count the run. The run is 3. Use the slope formula. \(m=\frac{\text{rise}}{\text{run}}\) Substitute the values of the rise and run. \(m=−23\) Simplify. \(m=−23\) The slope of the line is \(−23\). So y decreases by 2 units as x increases by 3 units.
Find the slope of the line shown.
- Answer
-
\(-\frac{4}{3}\)
Find the slope of the line shown.
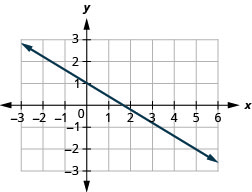
- Answer
-
\(-\frac{3}{5}\)
How do we find the slope of horizontal and vertical lines? To find the slope of the horizontal line, \(y=4\), we could graph the line, find two points on it, and count the rise and the run. Let’s see what happens when we do this, as shown in the graph below.
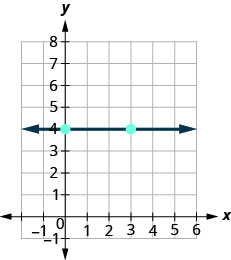
\( \begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{0}{3}} \\ {} &{m=0} \\{}&{\text{The slope of the horizontal line } y=4 \text{ is }0.} \\ \end{array} \nonumber\)
Let’s also consider a vertical line, the line \(x=3\), as shown in the graph.
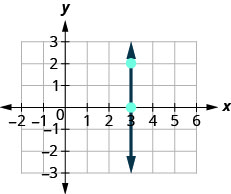
\( \begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{2}{0}} \\ \end{array} \nonumber\)
The slope is undefined since division by zero is undefined. So we say that the slope of the vertical line \(x=3\) is undefined.
All horizontal lines have slope 0. When the y-coordinates are the same, the rise is 0.
The slope of any vertical line is undefined. When the x-coordinates of a line are all the same, the run is 0.
The slope of a horizontal line, \(y=b\), is 0.
The slope of a vertical line, \(x=a\), is undefined.
Find the slope of each line: ⓐ \(x=8\) ⓑ \(y=−5\).
- Answer
-
ⓐ \(x=8\)
This is a vertical line. Its slope is undefined.
ⓑ \(y=−5\)
This is a horizontal line. It has slope 0.
Find the slope of the line: \(x=−4\).
- Answer
-
undefined
Find the slope of the line: \(y=7\).
- Answer
-
0
Sometimes we’ll need to find the slope of a line between two points when we don’t have a graph to count out the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but as we’ll see, there is a way to find the slope without graphing. Before we get to it, we need to introduce some algebraic notation.
We have seen that an ordered pair (x,y)(x,y) gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol (x,y)(x,y) be used to represent two different points? Mathematicians use subscripts to distinguish the points.
\( \begin{array} {ll} {(x_1, y_1)} &{\text{read “} x \text{ sub } 1, \space y \text{ sub } 1 \text{”}} \\ {(x_2, y_2)} &{\text{read “} x \text{ sub } 2, \space y \text{ sub } 2 \text{”}} \\ \end{array} \nonumber\)
We will use \((x_1,y_1)\) to identify the first point and \((x_2,y_2)\) to identify the second point.
If we had more than two points, we could use \((x_3,y_3)\), \((x_4,y_4)\), and so on.
Let’s see how the rise and run relate to the coordinates of the two points by taking another look at the slope of the line between the points \((2,3)\) and \((7,6)\), as shown in this graph.
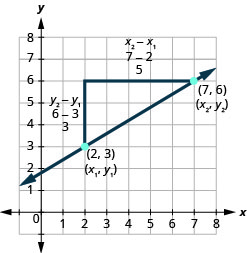
\( \begin{array} {ll} {\text{Since we have two points, we will use subscript notation.}} &{ \begin{pmatrix} x_1, & y_1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ 6 & 6 \end{pmatrix}} \\ {} &{m=\frac{\text{rise}}{\text{run}}} \\ {\text{On the graph, we counted the rise of 3 and the run of 5.}} &{m=\frac{3}{5}} \\ {\text{Notice that the rise of 3 can be found by subtracting the}} &{} \\ {y\text{-coordinates, 6 and 3, and the run of 5 can be found by}} &{} \\ {\text{subtracting the x-coordinates 7 and 2.}} &{} \\ {\text{We rewrite the rise and run by putting in the coordinates.}} &{m=\frac{6-3}{7-2}} \\ {} &{} \\ {\text{But 6 is } y_2 \text{, the y-coordinate of the second point and 3 is }y_1 \text{, the y-coordinate}} &{} \\ {\text{of the first point. So we can rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{7-2}} \\ {\text{Also 7 is the x-coordinate of the second point and 2 is the x-coordinate}} &{} \\ {\text{of the first point. So again we rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ \end{array} \nonumber\)
We’ve shown that \(m=\frac{y_2−y_1}{x_2−x_1}\) is really another version of \(m=\frac{\text{rise}}{\text{run}}\). We can use this formula to find the slope of a line when we have two points on the line.
The slope of the line between two points \((x_1,y_1)\) and \((x_2,y_2)\) is:
\(m=\frac{y_2−y_1}{x_2−x_1}\).
The slope is:
\[y\text{ of the second point minus }y\text{ of the first point} \nonumber\] \[\text{over} \nonumber\] \[x\text{ of the second point minus }x\text{ of the first point} \nonumber\]
Use the slope formula to find the slope of the line through the points \((−2,−3)\) and \((-7,4)\).
- Answer
-
\( \begin{array} {ll} {\text{We’ll call (−2,−3) point #1and (−7,4) point #2.}} &{ \begin{pmatrix} x_1, & y_1 \\ -2 & -3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ -7 & 4 \end{pmatrix}} \\ {\text{Use the slope formula.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{} \\ {\text{x of the second point minus x of the first point}} &{m=\frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify}}&{m=\frac{7}{-5}} \\ {} &{m=\frac{-7}{5}} \\ \end{array} \nonumber\)
Let’s verify this slope on the graph shown.
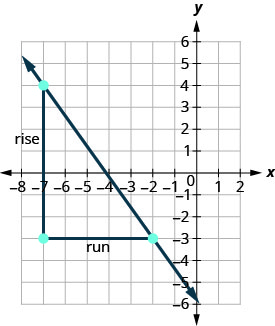
\[m=\frac{\text{rise}}{\text{run}} \nonumber\] \[m=\frac{7}{−5} \nonumber\] \[m=\frac{−7}{5} \nonumber\]
Use the slope formula to find the slope of the line through the pair of points: \((−3,4)\) and \((2,−1)\).
- Answer
-
\(-1\)
Use the slope formula to find the slope of the line through the pair of points: \((−2,6)\)and \((−3,−4)\).
- Answer
-
10
Graph a Line Given a Point and the Slope
Up to now, in this chapter, we have graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
We can also graph a line when we know one point and the slope of the line. We will start by plotting the point and then use the definition of slope to draw the graph of the line.
Graph the line passing through the point \((1,−1)\) whose slope is \(m=\frac{3}{4}\).
- Answer
-




You can check your work by finding a third point. Since the slope is \(m=\frac{3}{4}\), it can also be written as \(m=\frac{−3}{−4}\) (negative divided by negative is positive!). Go back to \((1,−1)\) and count out the rise, \(−3\), and the run, \(−4\).
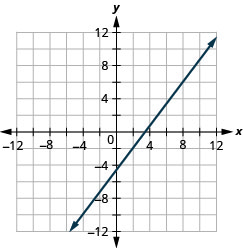
Graph the line passing through the point \((2,−2\) with the slope \(m=\frac{4}{3}\).
- Answer
-
.
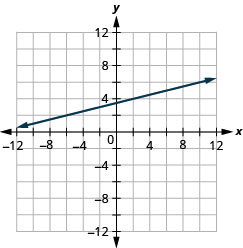
Graph the line passing through the point \((−2,3)\) with the slope \(m=\frac{1}{4}\).
- Answer
-
.
- Plot the given point.
- Use the slope formula \(m=\frac{\text{rise}}{\text{run}}\) to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
Graph a Line Using its Slope and Intercept
We have graphed linear equations by plotting points, using intercepts, recognizing horizontal and vertical lines, and using one point and the slope of the line. Once we see how an equation in slope–intercept form and its graph are related, we’ll have one more method we can use to graph lines.
Let’s look at the graph of the equation \(y=12x+3\) and find its slope and y-intercept.
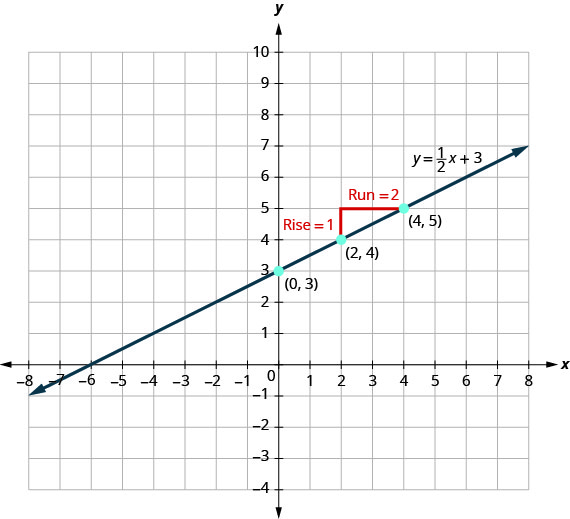
The red lines in the graph show us the rise is 1 and the run is 2. Substituting into the slope formula:
\[m=\frac{\text{rise}}{\text{run}} \nonumber\] \[m=\frac{1}{2} \nonumber\]
The y-intercept is \((0,3)\).
Look at the equation of this line.
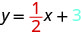
Look at the slope and y-intercept.

When a linear equation is solved for y, the coefficient of the x term is the slope and the constant term is the y-coordinate of the y-intercept. We say that the equation \(y=12x+3\) is in slope–intercept form. Sometimes the slope–intercept form is called the “y-form.”
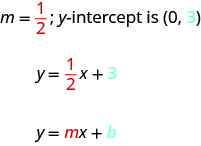
The slope–intercept form of an equation of a line with slope m and y-intercept, \((0,b)\) is \(y=mx+b\).
Let’s practice finding the values of the slope and y-intercept from the equation of a line.
Identify the slope and y-intercept of the line from the equation:
ⓐ \(y=−\frac{4}{7}x−2\) ⓑ \(x+3y=9\)
- Answer
-
ⓐ We compare our equation to the slope–intercept form of the equation.
Write the slope–intercept form of the equation of the line. 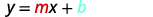
Write the equation of the line. 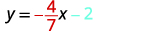
Identify the slope. 
Identify the y-intercept. 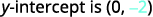
ⓑ When an equation of a line is not given in slope–intercept form, our first step will be to solve the equation for y.
Solve for y. x+3y=9x+3y=9 Subtract x from each side. 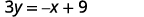
Divide both sides by 3. 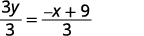
Simplify. 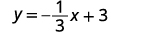
Write the slope–intercept form of the equation of the line. 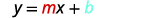
Write the equation of the line. 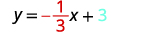
Identify the slope. 
Identify the y-intercept. 
Identify the slope and y-intercept from the equation of the line.
ⓐ \(y=\frac{2}{5}x−1\) ⓑ \(x+4y=8\)
- Answer
-
ⓐ \(m=\frac{2}{5}\); \((0,−1)\)
ⓑ \(m=−\frac{1}{4}\); \((0,2)\)
Identify the slope and y-intercept from the equation of the line.
ⓐ \(y=−\frac{4}{3} x+1\) ⓑ \(3x+2y=12\)
- Answer
-
ⓐ \(m=−\frac{4}{3}\); \((0,1)\)
ⓑ \(m=−\frac{3}{2}\); \((0,6)\)
We have graphed a line using the slope and a point. Now that we know how to find the slope and y-intercept of a line from its equation, we can use the y-intercept as the point, and then count out the slope from there.
Graph the line of the equation \(y=−x+4\) using its slope and y-intercept.
- Answer
-
\(y=mx+b\) The equation is in slope–intercept form. \(y=−x+4\) Identify the slope and y-intercept. \(m=−1\)
y-intercept is \((0,4)\)Plot the y-intercept. See the graph. Identify the rise over the run. \(m=−11\) Count out the rise and run to mark the second point. rise \(-1\), run \(1\)
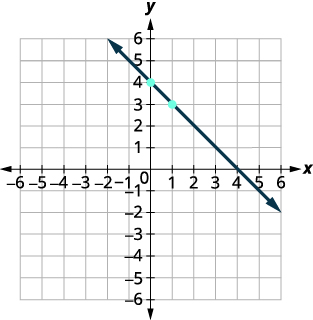
Draw the line as shown in the graph.
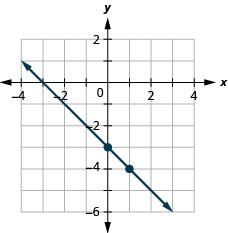
Graph the line of the equation \(y=−x−3\) using its slope and y-intercept.
- Answer
-
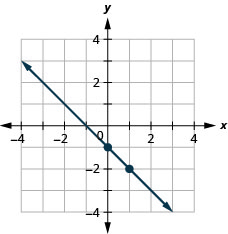
Graph the line of the equation \(y=−x−1\) using its slope and y-intercept.
- Answer
-
Now that we have graphed lines by using the slope and y-intercept, let’s summarize all the methods we have used to graph lines.

Choose the Most Convenient Method to Graph a Line
Now that we have seen several methods we can use to graph lines, how do we know which method to use for a given equation?
While we could plot points, use the slope–intercept form, or find the intercepts for any equation, if we recognize the most convenient way to graph a certain type of equation, our work will be easier.
Generally, plotting points is not the most efficient way to graph a line. Let’s look for some patterns to help determine the most convenient method to graph a line.
Here are five equations we graphed in this chapter, and the method we used to graph each of them.
\[ \begin{array} {lll} {} &{\textbf{Equation}} &{\textbf{Method}} \\ {\text{#1}} &{x=2} &{\text{Vertical line}} \\ {\text{#2}} &{y=−1} &{\text{Horizontal line}} \\ {\text{#3}} &{−x+2y=6} &{\text{Intercepts}} \\ {\text{#4}} &{4x−3y=12} &{\text{Intercepts}} \\ {\text{#5}} &{y=−x+4} &{\text{Slope–intercept}} \\ \end{array} \nonumber\]
Equations #1 and #2 each have just one variable. Remember, in equations of this form the value of that one variable is constant; it does not depend on the value of the other variable. Equations of this form have graphs that are vertical or horizontal lines.
In equations #3 and #4, both x and y are on the same side of the equation. These two equations are of the form Ax+By=C.Ax+By=C. We substituted y=0y=0 to find the x- intercept and x=0x=0 to find the y-intercept, and then found a third point by choosing another value for x or y.
Equation #5 is written in slope–intercept form. After identifying the slope and y-intercept from the equation we used them to graph the line.
This leads to the following strategy.
Consider the form of the equation.
- If it only has one variable, it is a vertical or horizontal line.
- \(x=a\) is a vertical line passing through the x-axis at a.
- \(y=b\) is a horizontal line passing through the y-axis at b.
- If y is isolated on one side of the equation, in the form \(y=mx+b\), graph by using the slope and y-intercept.
- Identify the slope and y-intercept and then graph.
- If the equation is of the form \(Ax+By=C\), find the intercepts.
- Find the x- and y-intercepts, a third point, and then graph.
Determine the most convenient method to graph each line:
ⓐ \(y=5\) ⓑ \(4x−5y=20\) ⓒ \(x=−3\) ⓓ \(y=−\frac{5}{9}x+8\)
- Answer
-
ⓐ \(y=5\)
This equation has only one variable, y. Its graph is a horizontal line crossing the y-axis at \(5\).
ⓑ \(4x−5y=20\)
This equation is of the form \(Ax+By=C\). The easiest way to graph it will be to find the intercepts and one more point.
ⓒ \(x=−3\)
There is only one variable, x. The graph is a vertical line crossing the x-axis at \(−3\).
ⓓ \(y=−\frac{5}{9}x+8\)
Since this equation is in \(y=mx+b\) form, it will be easiest to graph this line by using the slope and y-intercepts.
Determine the most convenient method to graph each line:
ⓐ \(3x+2y=12\) ⓑ \(y=4\) ⓒ \(y=\frac{1}{5}x−4\) ⓓ \(x=−7\).
- Answer
-
ⓐ intercepts ⓑ horizontal line ⓒ slope-intercept ⓓ vertical line
Determine the most convenient method to graph each line:
ⓐ \(x=6\) ⓑ \(y=−\frac{3}{4}x+1\) ⓒ \(y=−8\) ⓓ \(4x−3y=−1\).
- Answer
-
ⓐ vertical line ⓑ slope-intercept ⓒ horizontal line
ⓓ intercepts
Key Concepts
- Slope of a Line
- The slope of a line is \(m=\frac{\text{rise}}{\text{run}}\).
- The rise measures the vertical change and the run measures the horizontal change.
- How to find the slope of a line from its graph using \(m=\frac{\text{rise}}{\text{run}}\).
- Locate two points on the line whose coordinates are integers.
- Starting with one point, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope: \(m=\frac{\text{rise}}{\text{run}}\).
- Slope of a line between two points.
- The slope of the line between two points \((x_1,y_1)\) and \((x_2,y_2)\) is:
\[m=\frac{y_2−y_1}{x_2−x_1} \nonumber\].
- The slope of the line between two points \((x_1,y_1)\) and \((x_2,y_2)\) is:
- How to graph a line given a point and the slope.
- Plot the given point.
- Use the slope formula \(m=\frac{\text{rise}}{\text{run}}\) to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
- Slope Intercept Form of an Equation of a Line
- The slope–intercept form of an equation of a line with slope m and y-intercept, \((0,b)\) is \(y=mx+b\)


