2.4E: Exercises for Section 2.4

Taylor Polynomials

In exercises 1 - 8, find the Taylor polynomials of degree two approximating the given function centered at the given point.

1) \( f(x)=1+x+x^2\) at \( a=1\)

2) \( f(x)=1+x+x^2\) at \( a=−1\)

Answer

\( f(−1)=1;\;f′(−1)=−1;\;f''(−1)=2;\quad p_2(x)=1−(x+1)+(x+1)^2\)

3) \( f(x)=\cos(2x)\) at \( a=π\)

4) \( f(x)=\sin(2x)\) at \( a=\frac{π}{2}\)

Answer

\( f′(x)=2\cos(2x);\;f''(x)=−4\sin(2x);\quad p_2(x)=−2(x−\frac{π}{2})\)

5) \( f(x)=\sqrt{x}\) at \( a=4\)

6) \( f(x)=\ln x\) at \( a=1\)

Answer

\( f′(x)=\dfrac{1}{x};\; f''(x)=−\dfrac{1}{x^2};\quad p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2\)

7) \( f(x)=\dfrac{1}{x}\) at \( a=1\)

8) \( f(x)=e^x\) at \( a=1\)

Answer

\( p_2(x)=e+e(x−1)+\dfrac{e}{2}(x−1)^2\)

Taylor Remainder Theorem

In exercises 9 - 14, verify that the given choice of \(n\) in the remainder estimate \( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), where \(M\) is the maximum value of \( ∣f^{(n+1)}(z)∣\) on the interval between \(a\) and the indicated point, yields \( |R_n|≤\frac{1}{1000}\). Find the value of the Taylor polynomial \( p_n\) of \( f\) at the indicated point.

9) [T] \( \sqrt{10};\; a=9,\; n=3\)

10) [T] \( (28)^{1/3};\; a=27,\; n=1\)

Answer

\( \dfrac{d^2}{dx^2}x^{1/3}=−\dfrac{2}{9x^{5/3}}≥−0.00092…\) when \( x≥28\) so the remainder estimate applies to the linear approximation \( x^{1/3}≈p_1(27)=3+\dfrac{x−27}{27}\), which gives \( (28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}\), while \( (28)^{1/3}≈3.03658.\)

11) [T] \( \sin(6);\; a=2π,\; n=5\)

12) [T] \( e^2; \; a=0,\; n=9\)

Answer

Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the Taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). as \( e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887\)… whereas \( e^2≈7.3891.\)

13) [T] \( \cos(\frac{π}{5});\; a=0,\; n=4\)

14) [T] \( \ln(2);\; a=1,\; n=1000\)

Answer

Since \( \dfrac{d^n}{dx^n}(\ln x)=(−1)^{n−1}\dfrac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}\). One has \(\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\dfrac{(−1)^{n−1}}{n}≈0.6936\) whereas \( \ln(2)≈0.6931⋯.\)

Approximating Definite Integrals Using Taylor Series

15) Integrate the approximation \(\sin t≈t−\dfrac{t^3}{6}+\dfrac{t^5}{120}−\dfrac{t^7}{5040}\) evaluated at \( π\)t to approximate \(\displaystyle ∫^1_0\frac{\sin πt}{πt}\,dt\).

16) Integrate the approximation \( e^x≈1+x+\dfrac{x^2}{2}+⋯+\dfrac{x^6}{720}\) evaluated at \( −x^2\) to approximate \(\displaystyle ∫^1_0e^{−x^2}\,dx.\)

Answer

\(\displaystyle ∫^1_0\left(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720}\right)\,dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683\) whereas \(\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.\)

More Taylor Remainder Theorem Problems

In exercises 17 - 20, find the smallest value of \(n\) such that the remainder estimate \( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), where \(M\) is the maximum value of \( ∣f^{(n+1)}(z)∣\) on the interval between \(a\) and the indicated point, yields \( |R_n|≤\frac{1}{1000}\) on the indicated interval.

17) \( f(x)=\sin x\) on \( [−π,π],\; a=0\)

18) \( f(x)=\cos x\) on \( [−\frac{π}{2},\frac{π}{2}],\; a=0\)

Answer

Since \( f^{(n+1)}(z)\) is \(\sin z\) or \(\cos z\), we have \( M=1\). Since \( |x−0|≤\frac{π}{2}\), we seek the smallest \(n\) such that \( \dfrac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001\). The smallest such value is \( n=7\). The remainder estimate is \( R_7≤0.00092.\)

19) \( f(x)=e^{−2x}\) on \( [−1,1],a=0\)

20) \( f(x)=e^{−x}\) on \( [−3,3],a=0\)

Answer

Since \( f^{(n+1)}(z)=±e^{−z}\) one has \( M=e^3\). Since \( |x−0|≤3\), one seeks the smallest \(n\) such that \( \dfrac{3^{n+1}e^3}{(n+1)!}≤0.001\). The smallest such value is \( n=14\). The remainder estimate is \( R_{14}≤0.000220.\)

In exercises 21 - 24, the maximum of the right-hand side of the remainder estimate \( |R_1|≤\dfrac{max|f''(z)|}{2}R^2\) on \( [a−R,a+R]\) occurs at \(a\) or \( a±R\). Estimate the maximum value of \(R\) such that \( \dfrac{max|f''(z)|}{2}R^2≤0.1\) on \( [a−R,a+R]\) by plotting this maximum as a function of \(R\).

21) [T] \( e^x\) approximated by \( 1+x,\; a=0\)

22) [T] \( \sin x\) approximated by \( x,\; a=0\)

Answer

Since \( \sin x\) is increasing for small \( x\) and since \( \frac{d^2}{dx^2}\left(\sin x\right)=−\sin x\), the estimate applies whenever \( R^2\sin(R)≤0.2\), which applies up to \( R=0.596.\)

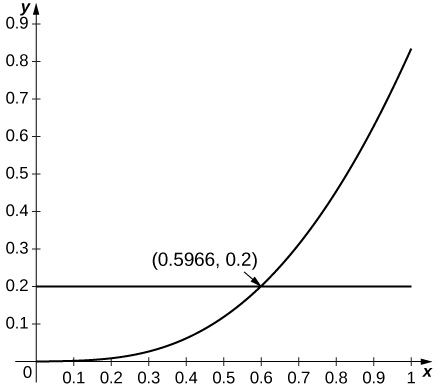
23) [T] \( \ln x\) approximated by \( x−1,\; a=1\)

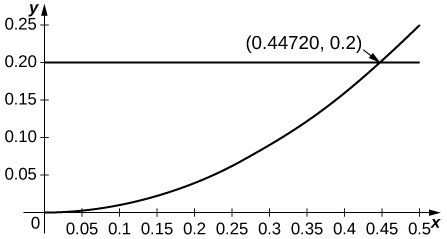
24) [T] \( \cos x\) approximated by \( 1,\; a=0\)

Answer

Since the second derivative of \( \cos x\) is \( −\cos x\) and since \( \cos x\) is decreasing away from \( x=0\), the estimate applies when \( R^2\cos R≤0.2\) or \( R≤0.447\).

Taylor Series

In exercises 25 - 35, find the Taylor series of the given function centered at the indicated point.

25) \(f(x) = x^4\) at \( a=−1\)

26) \(f(x) = 1+x+x^2+x^3\) at \( a=−1\)

Answer

\( (x+1)^3−2(x+1)^2+2(x+1)\)

27) \(f(x) = \sin x\) at \( a=π\)

28) \(f(x) = \cos x\) at \( a=2π\)

Answer

Values of derivatives are the same as for \( x=0\) so \(\displaystyle \cos x=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}\)

29) \(f(x) = \sin x\) at \( x=\frac{π}{2}\)

30) \(f(x) = \cos x\) at \( x=\frac{π}{2}\)

Answer

\( \cos(\frac{π}{2})=0,\;−\sin(\frac{π}{2})=−1\) so \(\displaystyle \cos x=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}\), which is also \( −\cos(x−\frac{π}{2})\).

31) \(f(x) = e^x\) at \( a=−1\)

32) \(f(x) = e^x\) at \( a=1\)

Answer

The derivatives are \( f^{(n)}(1)=e,\) so \(\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.\)

33) \(f(x) = \dfrac{1}{(x−1)^2}\) at \( a=0\) (Hint: Differentiate the Taylor Series for\( \dfrac{1}{1−x}\).)

34) \(f(x) = \dfrac{1}{(x−1)^3}\) at \( a=0\)

Answer

\(\displaystyle \frac{1}{(x−1)^3}=−\frac{1}{2}\frac{d^2}{dx^2}\left(\frac{1}{1−x}\right)=−\sum_{n=0}^∞\left(\frac{(n+2)(n+1)x^n}{2}\right)\)

35) \(\displaystyle F(x)=∫^x_0\cos(\sqrt{t})\,dt;\quad \text{where}\; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}\) at a=0 (Note: \( f\) is the Taylor series of \(\cos(\sqrt{t}).)\)

In exercises 36 - 44, compute the Taylor series of each function around \( x=1\).

36) \( f(x)=2−x\)

Answer

\( 2−x=1−(x−1)\)

37) \( f(x)=x^3\)

38) \( f(x)=(x−2)^2\)

Answer

\( ((x−1)−1)^2=(x−1)^2−2(x−1)+1\)

39) \( f(x)=\ln x\)

40) \( f(x)=\dfrac{1}{x}\)

Answer

\(\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n\)

41) \( f(x)=\dfrac{1}{2x−x^2}\)

42) \( f(x)=\dfrac{x}{4x−2x^2−1}\)

Answer

\(\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}\)

43) \( f(x)=e^{−x}\)

44) \( f(x)=e^{2x}\)

Answer

\(\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}\)

Maclaurin Series

[T] In exercises 45 - 48, identify the value of \(x\) such that the given series \(\displaystyle \sum_{n=0}^∞a_n\) is the value of the Maclaurin series of \( f(x)\) at \( x\). Approximate the value of \( f(x)\) using \(\displaystyle S_{10}=\sum_{n=0}^{10}a_n\).

45) \(\displaystyle \sum_{n=0}^∞\frac{1}{n!}\)

46) \(\displaystyle \sum_{n=0}^∞\frac{2^n}{n!}\)

Answer

\( x=e^2;\quad S_{10}=\dfrac{34,913}{4725}≈7.3889947\)

47) \(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}\)

48) \(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}\)

Answer

\(\sin(2π)=0;\quad S_{10}=8.27×10^{−5}\)

In exercises 49 - 52 use the functions \( S_5(x)=x−\dfrac{x^3}{6}+\dfrac{x^5}{120}\) and \( C_4(x)=1−\dfrac{x^2}{2}+\dfrac{x^4}{24}\) on \( [−π,π]\).

49) [T] Plot \(\sin^2x−(S_5(x))^2\) on \( [−π,π]\). Compare the maximum difference with the square of the Taylor remainder estimate for \( \sin x.\)

50) [T] Plot \(\cos^2x−(C_4(x))^2\) on \( [−π,π]\). Compare the maximum difference with the square of the Taylor remainder estimate for \( \cos x\).

Answer

The difference is small on the interior of the interval but approaches \( 1\) near the endpoints. The remainder estimate is \( |R_4|=\frac{π^5}{120}≈2.552.\)

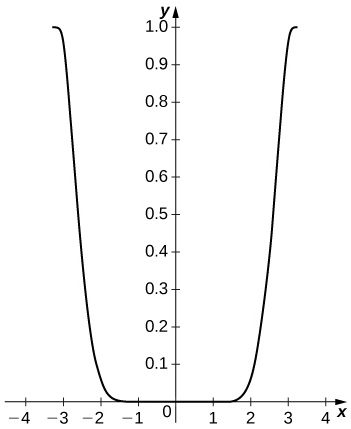
51) [T] Plot \( |2S_5(x)C_4(x)−\sin(2x)|\) on \( [−π,π]\).

52) [T] Compare \( \dfrac{S_5(x)}{C_4(x)}\) on \( [−1,1]\) to \( \tan x\). Compare this with the Taylor remainder estimate for the approximation of \( \tan x\) by \( x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}\).

Answer

The difference is on the order of \( 10^{−4}\) on \( [−1,1]\) while the Taylor approximation error is around \( 0.1\) near \( ±1\). The top curve is a plot of \(\tan^2x−\left(\dfrac{S_5(x)}{C_4(x)}\right)^2\) and the lower dashed plot shows \( t^2−\left(\dfrac{S_5}{C_4}\right)^2\).

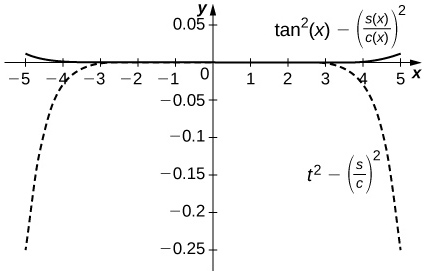
53) [T] Plot \( e^x−e_4(x)\) where \( e_4(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}\) on \( [0,2]\). Compare the maximum error with the Taylor remainder estimate.

54) (Taylor approximations and root finding.) Recall that Newton’s method \( x_{n+1}=x_n−\dfrac{f(x_n)}{f'(x_n)}\) approximates solutions of \( f(x)=0\) near the input \( x_0\).

a. If \( f\) and \( g\) are inverse functions, explain why a solution of \( g(x)=a\) is the value \( f(a)\) of \( f\).

b. Let \( p_N(x)\) be the \( N^{\text{th}}\) degree Maclaurin polynomial of \( e^x\). Use Newton’s method to approximate solutions of \( p_N(x)−2=0\) for \( N=4,5,6.\)

c. Explain why the approximate roots of \( p_N(x)−2=0\) are approximate values of \(\ln(2).\)

Answer

a. Answers will vary.
b. The following are the \( x_n\) values after \( 10\) iterations of Newton’s method to approximation a root of \( p_N(x)−2=0\): for \( N=4,x=0.6939...;\) for \( N=5,x=0.6932...;\) for \( N=6,x=0.69315...;.\) (Note: \( \ln(2)=0.69314...\))
c. Answers will vary.

Evaluating Limits using Taylor Series

In exercises 55 - 58, use the fact that if \(\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n\) converges in an interval containing \( c\), then \(\displaystyle \lim_{x→c}q(x)=a_0\) to evaluate each limit using Taylor series.

55) \(\displaystyle \lim_{x→0}\frac{\cos x−1}{x^2}\)

56) \(\displaystyle \lim_{x→0}\frac{\ln(1−x^2)}{x^2}\)

Answer

\( \dfrac{\ln(1−x^2)}{x^2}→−1\)

57) \(\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}\)

58) \(\displaystyle \lim_{x→0^+}\frac{\cos(\sqrt{x})−1}{2x}\)

Answer

\(\displaystyle \frac{\cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}\)