2.6E: Exercises
- Page ID
- 84739
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 8, evaluate the triple integrals ∭Ef(x,y,z)dV over the solid E.
1. f(x,y,z)=z,B={(x,y,z)|x2+y2≤9,x≤0,y≤0,0≤z≤1}
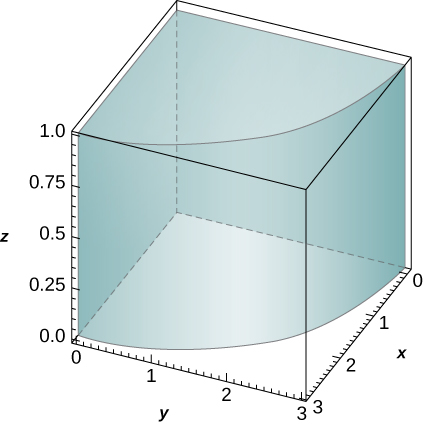
- Answer
- 9π8
2. f(x,y,z)=xz2, B={(x,y,z)|x2+y2≤16, x≥0, y≤0, −1≤z≤1}
3. f(x,y,z)=xy, B={(x,y,z)|x2+y2≤1, x≥0, x≥y, −1≤z≤1}
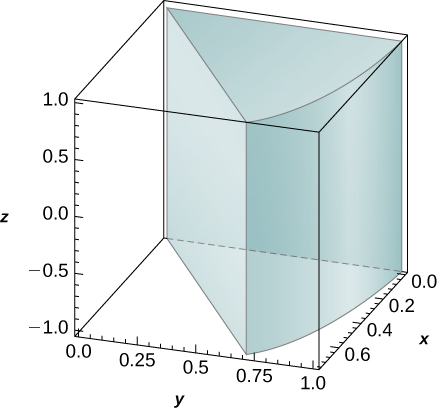
- Answer
- 18
4. f(x,y,z)=x2+y2, B={(x,y,z)|x2+y2≤4, x≥0, x≤y, 0≤z≤3}
5. f(x,y,z)=e√x2+y2, B={(x,y,z)|1≤x2+y2≤4, y≤0, x≤y√3, 2≤z≤3}
- Answer
- πe26
6. f(x,y,z)=√x2+y2, B={(x,y,z)|1≤x2+y2≤9, y≤0, 0≤z≤1}
7. a. Let B be a cylindrical shell with inner radius a outer radius b, and height c where 0<a<b and c>0. Assume that a function F defined on B can be expressed in cylindrical coordinates as F(x,y,z)=f(r)+h(z), where f and h are differentiable functions. If ∫baˉf(r)dr=0 and ˉh(0)=0, where ˉf and ˉh are antiderivatives of f and h, respectively, show that ∭BF(x,y,z)dV=2πc(bˉf(b)−aˉf(a))+π(b2−a2)ˉh(c).
b. Use the previous result to show that ∭B(z+sin√x2+y2)dx dy dz=6π2(π−2), where B is a cylindrical shell with inner radius π outer radius 2π, and height 2.
8. a. Let B be a cylindrical shell with inner radius a outer radius b and height c where 0<a<b and c>0. Assume that a function F defined on B can be expressed in cylindrical coordinates as F(x,y,z)=f(r)g(θ)f(z), where f, g, and h are differentiable functions. If ∫ba˜f(r)dr=0, where ˜f is an antiderivative of f, show that ∭BF(x,y,z)dV=[b˜f(b)−a˜f(a)][˜g(2π)−˜g(0)][˜h(c)−˜h(0)], where ˜g and ˜h are antiderivatives of g and h, respectively.
b. Use the previous result to show that ∭Bzsin√x2+y2dx dy dz=−12π2, where B is a cylindrical shell with inner radius π outer radius 2π, and height 2.
In exercises 9 - 12, the boundaries of the solid E are given in cylindrical coordinates.
a. Express the region E in cylindrical coordinates.
b. Convert the integral ∭Ef(x,y,z)dV to cylindrical coordinates.
9. E is bounded by the right circular cylinder r=4sinθ, the rθ-plane, and the sphere r2+z2=16.
- Answer
-
a. E={(r,θ,z)|0≤θ≤π, 0≤r≤4sinθ, 0≤z≤√16−r2}
b. ∫π0∫4sinθ0∫√16−r20f(r,θ,z)rdz dr dθ
10. E is bounded by the right circular cylinder r=cosθ, the rθ-plane, and the sphere r2+z2=9.
11. E is located in the first octant and is bounded by the circular paraboloid z=9−3r2, the cylinder r=√3, and the plane r(cosθ+sinθ)=20−z.
- Answer
-
a. E={(r,θ,z)|0≤θ≤π2, 0≤r≤√3, 9−r2≤z≤10−r(cosθ+sinθ)}
b. ∫π/20∫√30∫10−r(cosθ+sinθ)9−r2f(r,θ,z)r dz dr dθ
12. E is located in the first octant outside the circular paraboloid z=10−2r2 and inside the cylinder r=√5 and is bounded also by the planes z=20 and θ=π4.
In exercises 13 - 16, the function f and region E are given.
a. Express the region E and the function f in cylindrical coordinates.
b. Convert the integral ∭Bf(x,y,z)dV into cylindrical coordinates and evaluate it.
13. f(x,y,z)=x2+y2, E={(x,y,z)|0≤x2+y2≤9, x≥0, y≥0, 0≤z≤x+3}
- Answer
-
a. E={(r,θ,z)|0≤r≤3, 0≤θ≤π2, 0≤z≤r cosθ+3},
f(r,θ,z)=1r cosθ+3b. ∫30∫π/20∫r cosθ+30rr cosθ+3dz dθ dr=9π4
14. f(x,y,z)=x2+y2, E={(x,y,z)|0≤x2+y2≤4, y≥0, 0≤z≤3−x}
15. f(x,y,z)=x, E={(x,y,z)|1≤y2+z2≤9, 0≤x≤1−y2−z2}
- Answer
-
a. y=r cosθ, z=r sinθ, x=z, E={(r,θ,z)|1≤r≤3, 0≤θ≤2π, 0≤z≤1−r2}, f(r,θ,z)=z;
b. ∫31∫2π0∫1−r20zr dz dθ dr=356π3
16. f(x,y,z)=y, E={(x,y,z)|1≤x2+z2≤9, 0≤y≤1−x2−z2}
In exercises 17 - 24, find the volume of the solid E whose boundaries are given in rectangular coordinates.
17. E is above the xy-plane, inside the cylinder x2+y2=1, and below the plane z=1.
- Answer
- π
18. E is below the plane z=1 and inside the paraboloid z=x2+y2.
19. E is bounded by the circular cone z=√x2+y2 and z=1.
- Answer
- π3
20. E is located above the xy-plane, below z=1, outside the one-sheeted hyperboloid x2+y2−z2=1, and inside the cylinder x2+y2=2.
21. E is located inside the cylinder x2+y2=1 and between the circular paraboloids z=1−x2−y2 and z=x2+y2.
- Answer
- π
22. E is located inside the sphere x2+y2+z2=1, above the xy-plane, and inside the circular cone z=√x2+y2.
23. E is located outside the circular cone x2+y2=(z−1)2 and between the planes z=0 and z=2.
- Answer
- 4π3
24. E is located outside the circular cone z=1−√x2+y2, above the xy-plane, below the circular paraboloid, and between the planes z=0 and z=2.
25. [T] Use a computer algebra system (CAS) to graph the solid whose volume is given by the iterated integral in cylindrical coordinates ∫π/2−π/2∫10∫rr2rdzdrdθ. Find the volume V of the solid. Round your answer to four decimal places.
- Answer
-
V=pi12≈0.2618
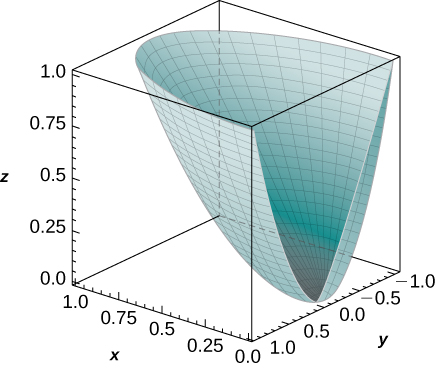
26. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates ∫π/20∫10∫rr4rdzdrdθ. Find the volume E of the solid. Round your answer to four decimal places.
27. Convert the integral ∫10∫√1−y2−√1−y2∫√x2+y2x2+y2xz dz dx dy into an integral in cylindrical coordinates.
- Answer
- ∫10∫π0∫rr2zr2 cosθdz dθ dr
28. Convert the integral ∫20∫y0∫10(xy+z)dz dx dy into an integral in cylindrical coordinates.
In exercises 29 - 32, evaluate the triple integral ∭Bf(x,y,z)dV over the solid B.
29. f(x,y,z)=1, B={(x,y,z)|x2+y2+z2≤90, z≥0}
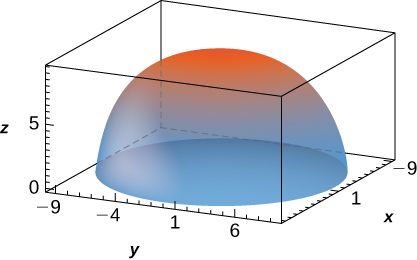
[Hide Solution]
- Answer
- 180π√10
30. f(x,y,z)=1−√x2+y2+z2, B={(x,y,z)|x2+y2+z2≤9, y≥0, z≥0}
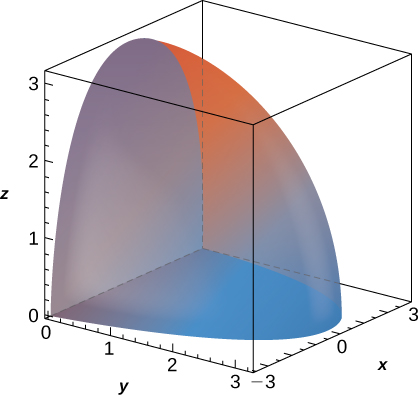
31. f(x,y,z)=√x2+y2, B is bounded above by the half-sphere x2+y2+z2=9 with z≥0 and below by the cone 2z2=x2+y2.
- Answer
- 81π(π−2)16
32. f(x,y,z)=√x2+y2, B is bounded above by the half-sphere x2+y2+z2=16 with z≥0 and below by the cone 2z2=x2+y2.
33. Show that if F(ρ,θ,φ)=f(ρ)g(θ)h(φ) is a continuous function on the spherical box B={(ρ,θ,φ)|a≤ρ≤b, α≤θ≤β, γ≤φ≤ψ}, then ∭BF dV=(∫baρ2f(ρ) dr)(∫βαg(θ) dθ)(∫ψγh(φ) sinφ dφ).
34. A function F is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as F(x,y,z)=f(ρ), where ρ=√x2+y2+z2. Show that ∭BF(x,y,z)dV=2π∫baρ2f(ρ)dρ, where B is the region between the upper concentric hemispheres of radii a and b centered at the origin, with 0<a<b and F a spherical function defined on B.
Use the previous result to show that ∭B(x2+y2+z2)√x2+y2+z2dV=21π, where B={(x,y,z)|1≤x2+y2+z2≤2, z≥0}.
35. Let B be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where 0<a<b. Consider F a function defined on B whose form in spherical coordinates (ρ,θ,φ) is F(x,y,z)=f(ρ)cosφ. Show that if g(a)=g(b)=0 and ∫bah(ρ)dρ=0, then ∭BF(x,y,z)dV=π24[ah(a)−bh(b)], where g is an antiderivative of f and h is an antiderivative of g.
Use the previous result to show that ∭B=zcos√x2+y2+z2√x2+y2+z2dV=3π22, where B is the region between the upper concentric hemispheres of radii π and 2π centered at the origin and situated in the first octant.
In exercises 36 - 39, the function f and region E are given.
a. Express the region E and function f in cylindrical coordinates.
b. Convert the integral ∭Bf(x,y,z)dV into cylindrical coordinates and evaluate it.
36. f(x,y,z)=z; E={(x,y,z)|0≤x2+y2+z2≤1, z≥0}
37. f(x,y,z)=x+y; E={(x,y,z)|1≤x2+y2+z2≤2, z≥0, y≥0}
- Answer
-
a. f(ρ,θ,φ)=ρ sinφ (cosθ+sinθ), E={(ρ,θ,φ)|1≤ρ≤2, 0≤θ≤π, 0≤φ≤π2};
b. ∫π0∫π/20∫21ρ3cosφ sinφ dρ dφ dθ=15π8
38. f(x,y,z)=2xy; E={(x,y,z)|√x2+y2≤z≤√1−x2−y2, x≥0, y≥0}
39. f(x,y,z)=z; E={(x,y,z)|x2+y2+z2−2x≤0, √x2+y2≤z}
- Answer
-
a. f(ρ,θ,φ)=ρ cosφ; E={(ρ,θ,φ)|0≤ρ≤2 cosφ, 0≤θ≤π2, 0≤φ≤π4};
b. ∫π/20∫π/40∫2 cosφ0ρ3sinφ cosφ dρ dφ dθ=7π24
In exercises 40 - 41, find the volume of the solid E whose boundaries are given in rectangular coordinates.
40. E={(x,y,z)|√x2+y2≤z≤√16−x2−y2, x≥0, y≥0}
41. E={(x,y,z)|x2+y2+z2−2z≤0, √x2+y2≤z}
- Answer
- π4
42. Use spherical coordinates to find the volume of the solid situated outside the sphere ρ=1 and inside the sphere ρ=cosφ, with φ∈[0,π2].
43. Use spherical coordinates to find the volume of the ball ρ≤3 that is situated between the cones φ=π4 and φ=π3.
- Answer
- 9π(√2−1)
44. Convert the integral ∫4−4∫√16−y2−√16−y2∫√16−x2−y2−√16−x2−y2(x2+y2+z2)dzdxdy into an integral in spherical coordinates.
45. Convert the integral ∫40∫√16−x20∫√16−x2−y2−√16−x2−y2(x2+y2+z2)2dz dy dx into an integral in spherical coordinates.
- Answer
- ∫π/20∫π/20∫40ρ6sinφdρdϕdθ
47. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates ∫ππ/2∫π/65π∫20ρ2sinφ dρ dφ dθ. Find the volume V of the solid. Round your answer to three decimal places.
- Answer
-
V=4π√33≈7.255
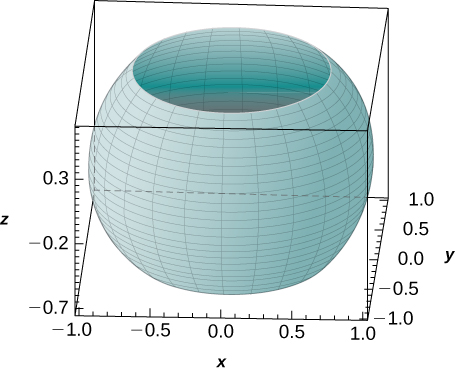
48. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates as ∫2π0∫π/43π/4∫10ρ2sinφ dρ dφ dθ. Find the volume V of the solid. Round your answer to three decimal places.
49. [T] Use a CAS to evaluate the integral ∭E(x2+y2)dV where E lies above the paraboloid z=x2+y2 and below the plane z=3y.
- Answer
- 343π32
50. [T]
a. Evaluate the integral ∭Ee√x2+y2+z2dV, where E is bounded by spheres 4x2+4y2+4z2=1 and x2+y2+z2=1.
b. Use a CAS to find an approximation of the previous integral. Round your answer to two decimal places.
51. Express the volume of the solid inside the sphere x2+y2+z2=16 and outside the cylinder x2+y2=4 as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
- Answer
- \displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ and \displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi
52. Express the volume of the solid inside the sphere x^2 + y^2 + z^2 = 16 and outside the cylinder x^2 + y^2 = 4 that is located in the first octant as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
53. The power emitted by an antenna has a power density per unit volume given in spherical coordinates by p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} \cos^2 \theta \space \sin^4 \varphi, where P_0 is a constant with units in watts. The total power within a sphere B of radius r meters is defined as \displaystyle P = \iiint_B p(\rho,\theta,\varphi) \, dV. Find the total power P.
- Answer
- P = \frac{32P_0 \pi}{3} watts
54. Use the preceding exercise to find the total power within a sphere B of radius 5 meters when the power density per unit volume is given by p(\rho, \theta,\varphi) = \frac{30}{\rho^2} \cos^2 \theta \sin^4 \varphi.
55. A charge cloud contained in a sphere B of radius r centimeters centered at the origin has its charge density given by q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}, where k > 0. The total charge contained in B is given by \displaystyle Q = \iiint_B q(x,y,z) \, dV. Find the total charge Q.
- Answer
- Q = kr^4 \pi \mu C
56. Use the preceding exercise to find the total charge cloud contained in the unit sphere if the charge density is q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

