2.8E: Exercises
- Last updated
- Sep 14, 2021
- Save as PDF
- Page ID
- 84743
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 6, the function T:S→R, T(u,v)=(x,y) on the region S={(u,v)|0≤u≤1, 0≤v≤1} bounded by the unit square is given, where R∈R2 is the image of S under T.
a. Justify that the function T is a C1 transformation.
b. Find the images of the vertices of the unit square S through the function T.
c. Determine the image R of the unit square S and graph it.
1. x=2u, y=3v
2. x=u2, y=v3
- Answer
-
a. T(u,v)=(g(u,v), h(u,v), x=g(u,v)=u2 and y=h(u,v)=v3. The functions g and h are continuous and differentiable, and the partial derivatives gu(u,v)=12, gv(u,v)=0, hu(u,v)=0 and hv(u,v)=13 are continuous on S;
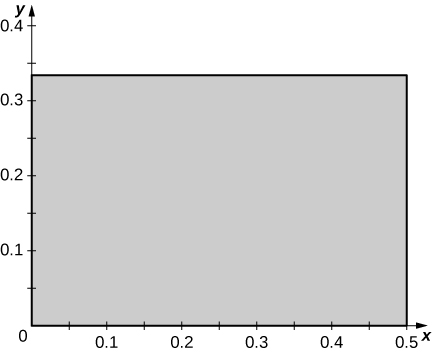
b. T(0,0)=(0,0), T(1,0)=(12,0), T(0,1)=(0,13), and T(1,1)=(12,13);
c. R is the rectangle of vertices (0,0), (0,13), (12,13), and (0,13) in the xy-plane; the following figure.
3. x=u−v, y=u+v
4. x=2u−v, y=u+2v
- Answer
-
a. T(u,v)=(g(u,v), h(u,v), x=g(u,v)=2u−v and y=h(u,v)=u+2v. The functions g and h are continuous and differentiable, and the partial derivatives gu(u,v)=2, gv(u,v)=−1, hu(u,v)=1 and hv(u,v)=2 are continuous on S;
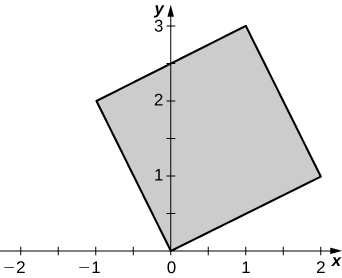
b. T(0,0)=(0,0), T(1,0)=(2,1), T(0,1)=(−1,2), and T(1,1)=(1,3);
c. R is the parallelogram of vertices (0,0), (2,1) (1,3), and (−1,2) in the xy-plane; the following figure.
5. x=u2, y=v2
6. x=u3, y=v3
- Answer
-
a. T(u,v)=(g(u,v), h(u,v), x=g(u,v)=u3 and y=h(u,v)=v3. The functions g and h are continuous and differentiable, and the partial derivatives gu(u,v)=3u2, gv(u,v)=0, hu(u,v)=0 and hv(u,v)=3v2 are continuous on S;
b. T(0,0)=(0,0), T(1,0)=(1,0), T(0,1)=(0,1), and T(1,1)=(1,1);
c. R is the unit square in the xy-plane see the figure in the answer to the previous exercise.
In exercises 7 - 12, determine whether the transformations T:S→R are one-to-one or not.
7. x=u2, y=v2, where S is the rectangle of vertices (−1,0), (1,0), (1,1), and (−1,1).
8. x=u4, y=u2+v, where S is the triangle of vertices (−2,0), (2,0), and (0,2).
- Answer
- T is not one-to-one: two points of S have the same image. Indeed, T(−2,0)=T(2,0)=(16,4).
9. x=2u, y=3v, where S is the square of vertices (−1,1), (−1,−1), (1,−1), and (1,1).
10. T(u,v)=(2u−v,u), where S is the triangle with vertices (−1,1),(−1,−1), and (1,−1).
- Answer
- T is one-to-one: We argue by contradiction. T(u1,v1)=T(u2,v2) implies 2u1−v1=2u2−v2 and u1=u2. Thus, u1=u+2 and v1=v2.
11. x=u+v+w, y=u+v, z=w, where S=R=R3.
12. x=u2+v+w, y=u2+v, z=w, where S=R=R3.
- Answer
- T is not one-to-one: T(1,v,w)=(−1,v,w)
In exercises 13 - 18, the transformations T:R→S are one-to-one. Find their related inverse transformations T−1:R→S.
13. x=4u, y=5v, where S=R=R2.
14. x=u+2v, y=−u+v, where S=R=R2.
- Answer
- u=x−2y3, v=x+y3
15. x=e2u+v, y=eu−v, where S=R2 and R={(x,y)|x>0, y>0}
16. x=lnu, y=ln(uv), where S={(u,v)|u>0, v>0} and R=R2.
- Answer
- u=ex, v=e−x+y
17. x=u+v+w, y=3v, z=2w, where S=R=R3.
18. x=u+v, y=v+w, z=u+w, where S=R=R3.
- Answer
- u=x−y+z2, v=x+y−z2, w=−x+y+z2
In exercises 19 - 22, the transformation T:S→R, T(u,v)=(x,y) and the region R⊂R2 are given. Find the region S⊂R2.
19. x=au, y=bv, R={(x,y)|x2+y2≤a2b2} where a,b>0
20. x=au, y=bc, R={(x,y)|x2a2+y2b2≤1}, where a,b>0
- Answer
- S={(u,v)|u2+v2≤1}
21. x=ua, y=vb, z=wc, R={(x,y)|x2+y2+z2≤1}, where a,b,c>0
22. x=au, y=bv, z=cw, R={(x,y)|x2a2−y2b2−z2c2≤1, z>0}, where a,b,c>0
- Answer
- R={(u,v,w)|u2−v2−w2≤1, w>0}
In exercises 23 - 32, find the Jacobian J of the transformation.
23. x=u+2v, y=−u+v
24. x=u32, y=vu2
- Answer
- 32
25. x=e2u−v, y=eu+v
26. x=uev, y=e−v
- Answer
- −1
27. x=u cos(ev), y=u sin(ev)
28. x=v sin(u2), y=v cos(u2)
- Answer
- 2uv
29. x=u coshv, y=u sinhv, z=w
30. x=v cosh(1u), y=v sinh(1u), z=u+w2
- Answer
- vu2
31. x=u+v, y=v+w, z=u
32. x=u−v, y=u+v, z=u+v+w
- Answer
- 2
33. The triangular region R with the vertices (0,0), (1,1), and (1,2) is shown in the following figure.
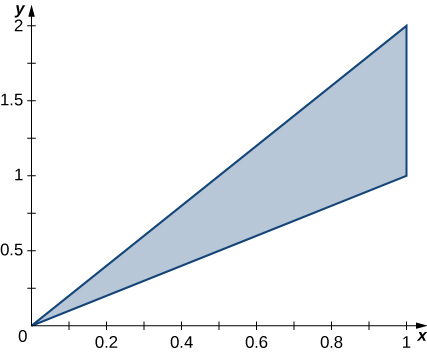
a. Find a transformation T:S→R, T(u,v)=(x,y)=(au+bv+dv), where a,b,c, and d are real numbers with ad−bc≠0 such that T−1(0,0)=(0,0), T−1(1,1)=(1,0), and T−1(1,2)=(0,1).
b. Use the transformation T to find the area A(R) of the region R.
34. The triangular region R with the vertices (0,0), (2,0), and (1,3) is shown in the following figure.
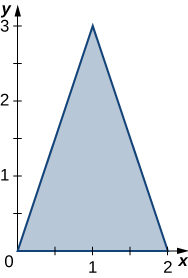
a. Find a transformation T:S→R, T(u,v)=(x,y)=(au+bv+dv), where a,b,c, and d are real numbers with ad−bc≠0 such that T−1(0,0)=(0,0), T−1(2,0)=(1,0), and T−1(1,3)=(0,1).
b. Use the transformation T to find the area A(R) of the region R.
- Answer
-
a. T(u,v)=(2u+v, 3v)
b. The area of R is A(R)=∫30∫(6−y)/3y/3dxdy=∫10∫1−u0|∂(x,y)∂(u,v)|dv du=∫10∫1−u06dvdu=3.
In exercises 35 - 36, use the transformation u=y−x, v=y, to evaluate the integrals on the parallelogram R of vertices (0,0), (1,0), (2,1), and (1,1) shown in the following figure.
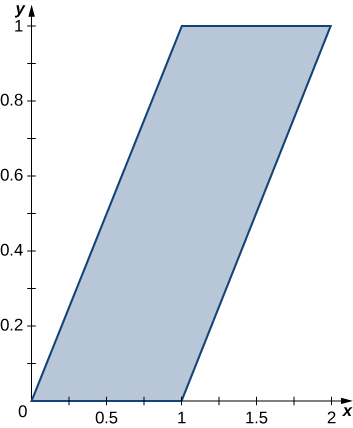
35. ∬R(y−x)dA
36. ∬R(y2−xy)dA
- Answer
- −14
In exercises 37 - 38, use the transformation y=x=u, x+y=v to evaluate the integrals on the square R determined by the lines y=x, y=−x+2, y=x+2, and y=−x shown in the following figure.
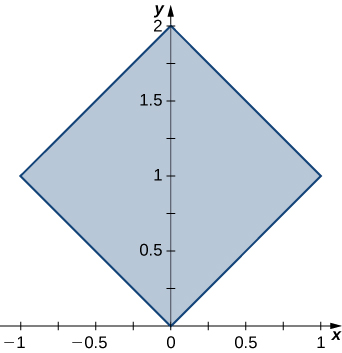
37. ∬Rex+ydA
38. ∬Rsin(x−y)dA
- Answer
- −1+cos2
In exercises 39 - 40, use the transformation x=u, 5y=v to evaluate the integrals on the region R bounded by the ellipse x2+25y2=1 shown in the following figure.
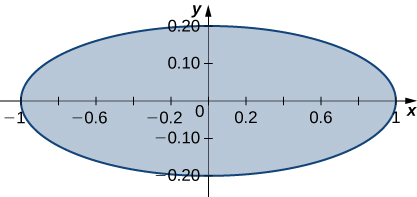
39. ∬R√x2+25y2dA
40. ∬R(x2+25y2)2dA
- Answer
- π15
In exercises 41 - 42, use the transformation u=x+y, v=x−y to evaluate the integrals on the trapezoidal region R determined by the points (1,0), (2,0), (0,2), and (0,1) shown in the following figure.
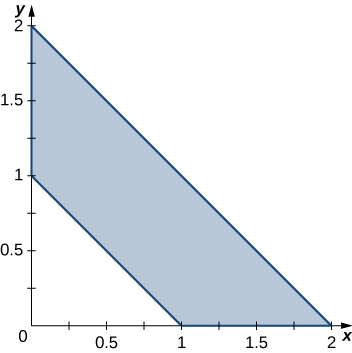
41. ∬R(x2−2xy+y2) ex+ydA
42. ∬R(x3+3x2y+3xy2+y3)dA
- Answer
- 315
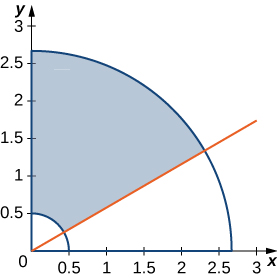
43. The circular annulus sector R bounded by the circles 4x2+4y2=1 and 9x2+9y2=64, the line x=y√3, and the y-axis is shown in the following figure. Find a transformation T from a rectangular region S in the rθ-plane to the region R in the xy-plane. Graph S.
44. The solid R bounded by the circular cylinder x2+y2=9 and the planes z=0, z=1, x=0, and y=0 is shown in the following figure. Find a transformation T from a cylindrical box S in rθz-space to the solid R in xyz-space.
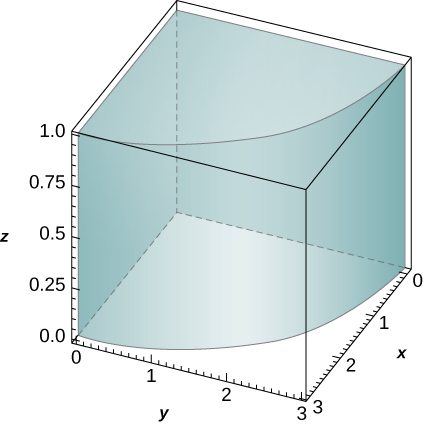
- Answer
- T(r,θ,z)=(r cosθ, r sinθ, z); S=[0,3]×[0,π2]×[0,1] in the rθz-space
45. Show that ∬Rf(√x23+y23)dA=2π√15∫10f(ρ)ρ dρ, where f is a continuous function on [0,1] and R is the region bounded by the ellipse 5x2+3y2=15.
46. Show that ∭Rf(√16x2+4y2+z2)dV=π2∫10f(ρ)ρ2dρ, where f is a continuous function on [0,1] and R is the region bounded by the ellipsoid 16x2+4y2+z2=1.
47. [T] Find the area of the region bounded by the curves xy=1, xy=3, y=2x, and y=3x by using the transformation u=xy and v=yx. Use a computer algebra system (CAS) to graph the boundary curves of the region R.
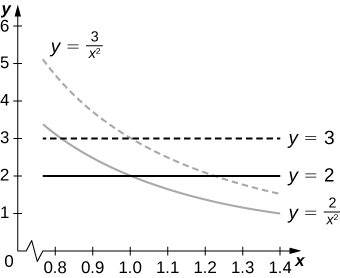
48. [T] Find the area of the region bounded by the curves x2y=2, x2y=3, y=x, and y=2x by using the transformation u=x2y and v=yx. Use a CAS to graph the boundary curves of the region R.
- Answer
-
The area of R is 10−4√6; the boundary curves of R are graphed in the following figure.
49. Evaluate the triple integral ∫10∫21∫z+1z(y+1) dx dy dz by using the transformation u=x−z, v=3y, and w=z2.
50. Evaluate the triple integral ∫20∫64∫3z+23z(5−4y) dx dy dz by using the transformation u=x−3z, v=4y, and w=z.
- Answer
- 8
51. A transformation T:R2→R2, T(u,v)=(x,y) of the form x=au+bv, y=cu+dv, where a,b,c, and d are real numbers, is called linear. Show that a linear transformation for which ad−bc≠0 maps parallelograms to parallelograms.
52. A transformation Tθ:R2→R2, Tθ(u,v)=(x,y) of the form x=u cosθ−v sinθ, y=u sinθ+v cosθ, is called a rotation angle θ. Show that the inverse transformation of Tθ satisfies T−1θ=T−θ where T−θ is the rotation of angle −θ.
53. [T] Find the region S in the uv-plane whose image through a rotation of angle π4 is the region R enclosed by the ellipse x2+4y2=1. Use a CAS to answer the following questions.
a. Graph the region S.
b. Evaluate the integral ∬Se−2uvdudv. Round your answer to two decimal places.
54. [T] The transformations Ti:R2→R2, i=1,...,4, defined by T1(u,v)=(u,−v), T2(u,v)=(−u,v), T3(u,v)=(−u,−v), and T4(u,v)=(v,u) are called reflections about the x-axis, y-axis origin, and the line y=x, respectively.
a. Find the image of the region S={(u,v)|u2+v2−2u−4v+1≤0} in the xy-plane through the transformation T1∘T2∘T3∘T4.
b. Use a CAS to graph R.
c. Evaluate the integral ∬Ssin(u2)dudv by using a CAS. Round your answer to two decimal places.
- Answer
-
a. R={(x,y)|y2+x2−2y−4x+1≤0};
b. R is graphed in the following figure;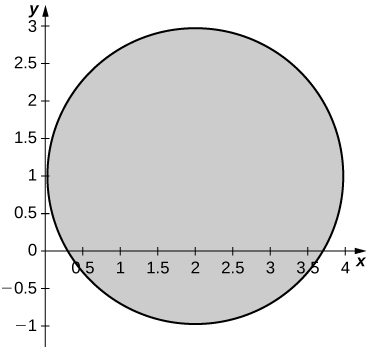
c. 3.16
55. [T] The transformations Tk,1,1:R3→R3, Tk,1,1(u,v,w)=(x,y,z) of the form x=ku, y=v, z=w, where k≠1 is a positive real number, is called a stretch if k>1 and a compression if 0<k<1 in the x-direction. Use a CAS to evaluate the integral ∭Se−(4x2+9y2+25z2)dxdydz on the solid S={(x,y,z)|4x2+9y2+25z2≤1} by considering the compression T2,3,5(u,v,w)=(x,y,z) defined by x=u2, y=v3, and z=w5. Round your answer to four decimal places.
56. [T] The transformation Ta,0:R2→R2, Ta,0(u,v)=(u+av,v), where a≠0 is a real number, is called a shear in the x-direction. The transformation, Tb,0:R2→R2, To,b(u,v)=(u,bu+v), where b≠0 is a real number, is called a shear in the y-direction.
a. Find transformations T0,2∘T3,0.
b. Find the image R of the trapezoidal region S bounded by u=0, v=0, v=1, and v=2−u through the transformation T0,2∘T3,0.
c. Use a CAS to graph the image R in the xy-plane.
d. Find the area of the region R by using the area of region S.
- Answer
-
a. T0,2∘T3,0(u,v)=(u+3v,2u+7v);
b. The image S is the quadrilateral of vertices (0,0), (3,7), (2,4), and (4,9);
c. S is graphed in the following figure;
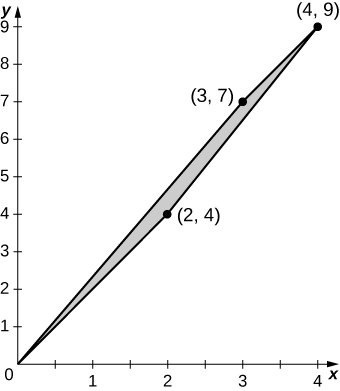
d. 32
57. Use the transformation, x=au, y=av, z=cw and spherical coordinates to show that the volume of a region bounded by the spheroid x2+y2a2+z2c2=1 is 4πa2c3.
58. Find the volume of a football whose shape is a spheroid x2+y2a2+z2c2=1 whose length from tip to tip is 11 inches and circumference at the center is 22 inches. Round your answer to two decimal places.
- Answer
- 26623π≈282.45 in3
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

