3.4E: Exercises

1. True or False? If vector field $\vecs F$ is conservative on the open and connected region $D$, then line integrals of $\vecs F$ are path independent on $D$, regardless of the shape of $D$.

Answer

True

2. True or False? Function $\vecs r(t)=\vecs a+t(\vecs b−\vecs a)$, where $0≤t≤1$, parameterizes the straight-line segment from $\vecs a$ to $\vecs b$.

Answer

True

3. True or False? Vector field $\vecs F(x,y,z)=(y\sin z)\,\mathbf{\hat i}+(x\sin z)\,\mathbf{\hat j}+(xy\cos z)\,\mathbf{\hat k}$ is conservative.

Answer

True

4. True or False? Vector field $\vecs F(x,y,z)=y\,\mathbf{\hat i}+(x+z)\,\mathbf{\hat j}−y\,\mathbf{\hat k}$ is conservative.

5. Justify the Fundamental Theorem of Line Integrals for $\displaystyle \int _C\vecs F·d\vecs r$ in the case when $\vecs{F}(x,y)=(2x+2y)\,\mathbf{\hat i}+(2x+2y)\,\mathbf{\hat j}$ and $C$ is a portion of the positively oriented circle $x^2+y^2=25$ from $(5, 0)$ to $(3, 4).$

Answer

$\displaystyle \int _C \vecs F·d\vecs r=24$ units of work

6. [T] Find $\displaystyle \int _C\vecs F·d\vecs r,$ where $\vecs{F}(x,y)=(ye^{xy}+\cos x)\,\mathbf{\hat i}+\left(xe^{xy}+\frac{1}{y^2+1}\right)\,\mathbf{\hat j}$ and $C$ is a portion of curve $y=\sin x$ from $x=0$ to $x=\frac{π}{2}$.

7. [T] Evaluate line integral $\displaystyle \int _C\vecs F·d\vecs r$, where $\vecs{F}(x,y)=(e^x\sin y−y)\,\mathbf{\hat i}+(e^x\cos y−x−2)\,\mathbf{\hat j}$, and $C$ is the path given by $\vecs r(t)=(t^3\sin\frac{πt}{2})\,\mathbf{\hat i}−(\frac{π}{2}\cos(\frac{πt}{2}+\frac{π}{2}))\,\mathbf{\hat j}$ for $0≤t≤1$.

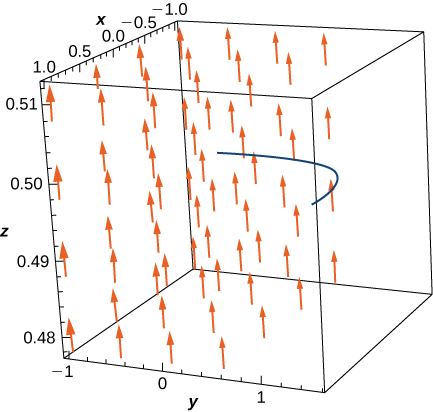
Answer

$\displaystyle \int _C\vecs F·d\vecs r=\left(e−\frac{3π}{2}\right)$ units of work

For the following exercises, determine whether the vector field is conservative and, if it is, find the potential function.

8. $\vecs{F}(x,y)=2xy^3\,\mathbf{\hat i}+3y^2x^2\,\mathbf{\hat j}$

9. $\vecs{F}(x,y)=(−y+e^x\sin y)\,\mathbf{\hat i}+((x+2)e^x\cos y)\,\mathbf{\hat j}$

Answer

Not conservative

10. $\vecs{F}(x,y)=(e^{2x}\sin y)\,\mathbf{\hat i}+(e^{2x}\cos y)\,\mathbf{\hat j}$

11. $\vecs{F}(x,y)=(6x+5y)\,\mathbf{\hat i}+(5x+4y)\,\mathbf{\hat j}$

Answer

Conservative, $f(x,y)=3x^2+5xy+2y^2+k$

12. $\vecs{F}(x,y)=(2x\cos(y)−y\cos(x))\,\mathbf{\hat i}+(−x^2\sin(y)−\sin(x))\,\mathbf{\hat j}$

13. $\vecs{F}(x,y)=(ye^x+\sin(y))\,\mathbf{\hat i}+(e^x+x\cos(y))\,\mathbf{\hat j}$

Answer

Conservative, $f(x,y)=ye^x+x\sin(y)+k$

For the following exercises, evaluate the line integrals using the Fundamental Theorem of Line Integrals.

14. $\displaystyle ∮_C(y\,\mathbf{\hat i}+x\,\mathbf{\hat j})·d\vecs r,$ where $C$ is any path from $(0, 0)$ to $(2, 4)$

15. $\displaystyle ∮_C(2y\,dx+2x\,dy),$ where $C$ is the line segment from $(0, 0)$ to $(4, 4)$

Answer

$\displaystyle ∮_C(2y\,dx+2x\,dy)=32$ units of work

16. [T] $\displaystyle ∮_C\left[\arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}\right]\,dx+\left[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)\right]\,dy$, where $C$ is any smooth curve from $(1, 1)$ to $(−1,2).$

17. Find the conservative vector field for the potential function $f(x,y)=5x^2+3xy+10y^2.$

Answer

$\vecs{F}(x,y)=(10x+3y)\,\mathbf{\hat i}+(3x+20y)\,\mathbf{\hat j}$

For the following exercises, determine whether the vector field is conservative and, if so, find a potential function.

18. $\vecs{F}(x,y)=(12xy)\,\mathbf{\hat i}+6(x^2+y^2)\,\mathbf{\hat j}$

19. $\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}$

Answer

$\vecs F$ is not conservative.

20. $\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}$

21. $\vecs F(x,y,z)=(ye^z)\,\mathbf{\hat i}+(xe^z)\,\mathbf{\hat j}+(xye^z)\,\mathbf{\hat k}$

Answer

$\vecs F$ is conservative and a potential function is $f(x,y,z)=xye^z+k$.

22. $\vecs F(x,y,z)=(\sin y)\,\mathbf{\hat i}−(x\cos y)\,\mathbf{\hat j}+\,\mathbf{\hat k}$

23. $\vecs F(x,y,z)=\dfrac{1}{y}\,\mathbf{\hat i}-\dfrac{x}{y^2}\,\mathbf{\hat j}+(2z−1)\,\mathbf{\hat k}$

Answer

$\vecs F$ is conservative and a potential function is $f(x,y,z)=\dfrac{x}{y}+z^2-z+k.$

24. $\vecs F(x,y,z)=3z^2\,\mathbf{\hat i}−\cos y\,\mathbf{\hat j}+2xz\,\mathbf{\hat k}$

25. $\vecs F(x,y,z)=(2xy)\,\mathbf{\hat i}+(x^2+2yz)\,\mathbf{\hat j}+y^2\,\mathbf{\hat k}$

Answer

$\vecs F$ is conservative and a potential function is $f(x,y,z)=x^2y+y^2z+k.$

For the following exercises, determine whether the given vector field is conservative and find a potential function.

26. $\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}$

27. $\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+(x^2e^{x^2y})\,\mathbf{\hat j}$

Answer

$\vecs F$ is conservative and a potential function is $f(x,y)=e^{x^2y}+k$

For the following exercises, evaluate the integral using the Fundamental Theorem of Line Integrals.

28. Evaluate $\displaystyle \int _C\vecs ∇f·d\vecs r$, where $f(x,y,z)=\cos(πx)+\sin(πy)−xyz$ and $C$ is any path that starts at $(1,12,2)$ and ends at $(2,1,−1)$.

29. [T] Evaluate $\displaystyle \int _C\vecs ∇f·d\vecs r$, where $f(x,y)=xy+e^x$ and $C$ is a straight line from $(0,0)$ to $(2,1)$.

Answer

$\displaystyle \int _C\vecs F·d\vecs r=\left(e^2+1\right)$ units of work

30. [T] Evaluate $\displaystyle \int _C\vecs ∇f·d\vecs r,$ where $f(x,y)=x^2y−x$ and $C$ is any path in a plane from (1, 2) to (3, 2).

31. Evaluate $\displaystyle \int _C\vecs ∇f·d\vecs r,$ where $f(x,y,z)=xyz^2−yz$ and $C$ has initial point $(1, 2, 3)$ and terminal point $(3, 5, 2).$

Answer

$\displaystyle \int _C\vecs F·d\vecs r=38$ units of work

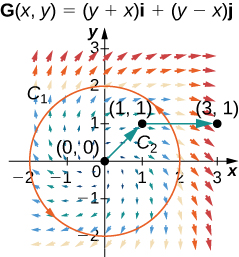
For the following exercises, let $\vecs{F}(x,y)=2xy^2\,\mathbf{\hat i}+(2yx^2+2y)\,\mathbf{\hat j}$ and $G(x,y)=(y+x)\,\mathbf{\hat i}+(y−x)\,\mathbf{\hat j}$, and let $C_1$ be the curve consisting of the circle of radius 2, centered at the origin and oriented counterclockwise, and $C_2$ be the curve consisting of a line segment from $(0, 0)$ to $(1, 1)$ followed by a line segment from $(1, 1)$ to $(3, 1)$.

              

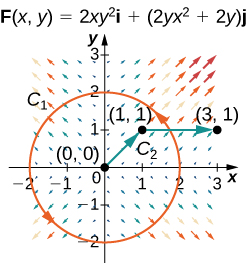
32. Calculate the line integral of $\vecs F$ over $C_1$.

33. Calculate the line integral of $\vecs G$ over $C_1$.

Answer

$\displaystyle ∮_{C_1}\vecs G·d\vecs r=−8π$ units of work

34. Calculate the line integral of $\vecs F$ over $C_2$.

35. Calculate the line integral of $\vecs G$ over $C_2$.

Answer

$\displaystyle ∮_{C_2}\vecs F·d\vecs r=7$ units of work

36. [T] Let $\vecs F(x,y,z)=x^2\,\mathbf{\hat i}+z\sin(yz)\,\mathbf{\hat j}+y\sin(yz)\,\mathbf{\hat k}$. Calculate $\displaystyle ∮_C\vecs F·d\vecs{r}$, where $C$ is a path from $A=(0,0,1)$ to $B=(3,1,2)$.

37. [T] Find line integral $\displaystyle ∮_C\vecs F·dr$ of vector field $\vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k}$ along curve $C$ parameterized by $\vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+t\cos(πt),1≤t≤4.$

Answer

$\displaystyle \int _C\vecs F·d\vecs r=159$ units of work

For exercises 38 - 40, show that the following vector fields are conservative. Then calculate $\displaystyle \int _C\vecs F·d\vecs r$ for the given curve.

38. $\vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}$; $C$ is the curve consisting of line segments from $(1,1)$ to $(0,2)$ to $(3,0).$

39. $\vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}$; $C$ is parameterized by $x=t^3−1,\;y=t^6−t$, for $0≤t≤1.$

Answer

$\displaystyle \int _C\vecs F·d\vecs r=−1$ units of work

40. [T] $\vecs{F}(x,y)=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}$; $C$ is the curve $\langle e^t,e^{t+1}\rangle,$ for $−1≤t≤0$.

41. The mass of Earth is approximately $6×10^{27}g$ and that of the Sun is 330,000 times as much. The gravitational constant is $6.7×10^{−8}cm^3/s^2·g$. The distance of Earth from the Sun is about $1.5×10^{12}cm$. Compute, approximately, the work necessary to increase the distance of Earth from the Sun by $1\;cm$.

Answer

$4×10^{31}$ erg

42. [T] Let $\vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}$. Evaluate the integral $\displaystyle \int _C\vecs F·d\vecs r$, where $\vecs r(t)=\langle\sqrt{t},t^3,e^{\sqrt{t}}\rangle,$ for $0≤t≤1.$

43. [T] Let $C:[1,2]→ℝ^2$ be given by $x=e^{t−1},y=\sin\left(\frac{π}{t}\right)$. Use a computer to compute the integral $\displaystyle \int _C\vecs F·d\vecs r=\int _C 2x\cos y\,dx−x^2\sin y\,dy$, where $\vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.$

Answer

$\displaystyle \int _C\vecs F·d\vecs s=0.4687$ units of work

44. [T] Use a computer algebra system to find the mass of a wire that lies along the curve $\vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k},$ where $0≤t≤1$, if the density is given by $d(t) = \dfrac{3}{2}t$.

45. Find the circulation and flux of field $\vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}$ around and across the closed semicircular path that consists of semicircular arch $\vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π$, followed by line segment $\vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.$

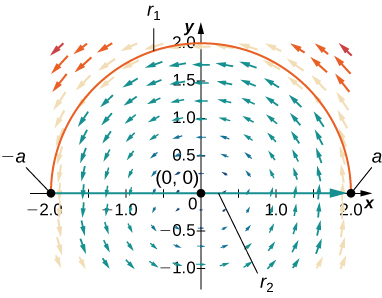
Answer

$\text{circulation}=πa^2$ and $\text{flux}=0$

46. Compute $\displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy,$ where $\vecs r(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.$

47. Complete the proof of the theorem titled THE PATH INDEPENDENCE TEST FOR CONSERVATIVE FIELDS by showing that $f_y=Q(x,y).$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.