3.7E: Exercises

Last updated
Save as PDF

Page ID: 84758

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 4, determine whether the statements are true or false.

1. If surface $S$ is given by $\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}$, then $\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx \, dy.$

Answer: True

2. If surface $S$ is given by $\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}$, then $\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx \, dy.$

3. Surface $\vecs r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle,$ for $ 0 \leq u \leq \pi, \, 0 \leq v \leq 2$ is the same surface $\vecs r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle,$ for $ 0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4$.

Answer: True

4. Given the standard parameterization of a sphere, normal vectors $\vecs t_u \times \vecs t_v$ are outward normal vectors.

In exercises 5 - 10, find parametric descriptions for the following surfaces.

5. Plane $3x - 2y + z = 2$

Answer: $\vecs r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle $ for $-\infty \leq u < \infty$ and $ - \infty \leq v < \infty$.

6. Paraboloid $z = x^2 + y^2$, for $0 \leq z \leq 9$.

7. Plane $2x - 4y + 3z = 16$

Answer: $\vecs r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle $ for $|u| < \infty$ and $|v| < \infty$.

8. The frustum of cone $z^2 = x^2 + y^2$, for $2 \leq z \leq 8$

9. The portion of cylinder $x^2 + y^2 = 9$ in the first octant, for $0 \leq z \leq 3$

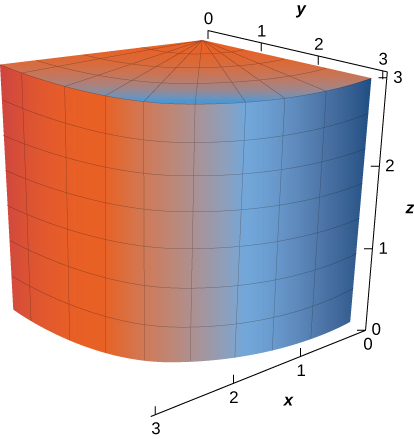
$A diagram in three dimensions of a section of a cylinder with radius 3. The center of its circular top is (0,0,3). The section exists for x, y, and z between 0 and 3.$

Answer: $\vecs r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle $ for $0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3$

10. A cone with base radius $r$ and height $h,$ where $r$ and $h$ are positive constants.

For exercises 11 - 12, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.

11. [T] Half cylinder $\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}$

Answer: $A = 87.9646$

12. [T] Plane $z = 10 - z - y$ above square $|x| \leq 2, \, |y| \leq 2$

In exercises 13 - 15, let $S$ be the hemisphere $x^2 + y^2 + z^2 = 4$, with $z \geq 0$, and evaluate each surface integral, in the counterclockwise direction.

13. $\displaystyle \iint_S z\, dS$

Answer: $\displaystyle \iint_S z \, dS = 8\pi$

14. $\displaystyle \iint_S (x - 2y) \, dS$

15. $\displaystyle \iint_S (x^2 + y^2) \, dS$

Answer: $\displaystyle \iint_S (x^2 + y^2) \, dS = 16 \pi$

In exercises 16 - 18, evaluate $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS$ for vector field $\vecs F$ where $\vecs N$ is an outward normal vector to surface $S$.

16. $\vecs F(x,y,z) = x\,\mathbf{\hat i}+ 2y\,\mathbf{\hat j} = 3z\,\mathbf{\hat k}$, and $S$ is that part of plane $15x - 12y + 3z = 6$ that lies above unit square $0 \leq x \leq 1, \, 0 \leq y \leq 1$.

17. $\vecs F(x,y) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j}$, and $S$ is hemisphere $z = \sqrt{1 - x^2 - y^2}$.

Answer: $\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{4\pi}{3}$

18. $\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}$, and $S$ is the portion of plane $z = y + 1$ that lies inside cylinder $x^2 + y^2 = 1$.

$A cylinder and an intersecting plane shown in three-dimensions. S is the portion of the plane z = y + 1 inside the cylinder x^2 + y ^2 = 1.$

In exercises 19 - 20, approximate the mass of the homogeneous lamina that has the shape of given surface $S$. Round to four decimal places.

19. [T] $S$ is surface $z = 4 - x - 2y$, with $z \geq 0, \, x \geq 0, \, y \geq 0; \, \xi = x.$

Answer: $m \approx 13.0639$

20. [T] $S$ is surface $z = x^2 + y^2$, with $z \leq 1; \, \xi = z$.

21. [T] $S$ is surface $x^2 + y^2 + x^2 = 5$, with $z \geq 1; \, \xi = \theta^2$.

Answer: $m \approx 228.5313$

22. Evaluate $\displaystyle \iint_S (y^2 z\,\mathbf{\hat i}+ y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}) \cdot dS,$ where $S$ is the surface of cube $-1 \leq x \leq 1, \, -1 \leq y \leq 1$, and $0 \leq z \leq 2$ in a counterclockwise direction.

23. Evaluate surface integral $\displaystyle \iint_S g \, dS,$ where $g(x,y,z) = xz + 2x^2 - 3xy$ and $S$ is the portion of plane $2x - 3y + z = 6$ that lies over unit square $R: 0 \leq x \leq 1, \, 0 \leq y \leq 1$.

Answer: $\displaystyle \iint_S g\,dS = 3 \sqrt{4}$

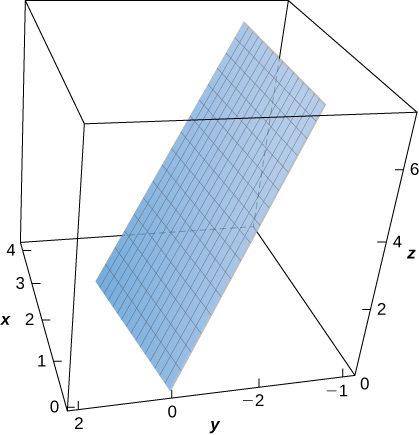
24. Evaluate $\displaystyle \iint_S (x + y + z)\, dS,$ where $S$ is the surface defined parametrically by $\vecs R(u,v) = (2u + v)\,\mathbf{\hat i} + (u - 2v)\,\mathbf{\hat j} + (u + 3v)\,\mathbf{\hat k}$ for $0 \leq u \leq 1$, and $0 \leq v \leq 2$.

$A three-dimensional diagram of the given surface, which appears to be a steeply sloped plane stretching through the (x,y) plane.$

25. [T] Evaluate $\displaystyle \iint_S (x - y^2 + z)\, dS,$ where $S$ is the surface defined parametrically by $\vecs R(u,v) = u^2\,\mathbf{\hat i} + v\,\mathbf{\hat j} + u\,\mathbf{\hat k}$ for $0 \leq u \leq 1, \, 0 \leq v \leq 1$.

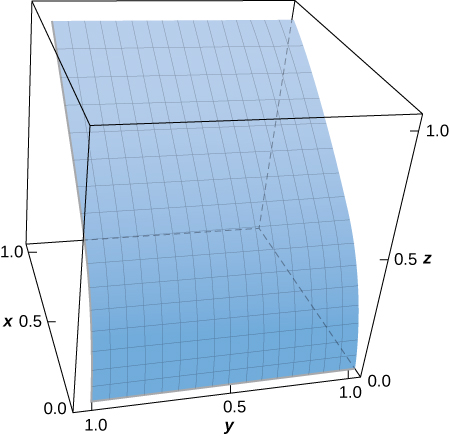
$A three-dimensional diagram of the given surface, which appears to be a curve with edges parallel to the y-axis. It increases in x components and decreases in z components the further it is from the y axis.$

Answer: $\displaystyle \iint_S (x^2 + y - z) \, dS \approx 0.9617$

26. [T] Evaluate where $S$ is the surface defined by $\vecs R(u,v) = u\,\mathbf{\hat i} - u^2\,\mathbf{\hat j} + v\,\mathbf{\hat k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1$ for $0 \leq u \leq 1, \, 0 \leq v \leq 2$.

27. Evaluate $\displaystyle \iint_S (x^2 + y^2) \, dS,$ where $S$ is the surface bounded above hemisphere $z = \sqrt{1 - x^2 - y^2}$, and below by plane $z = 0$.

Answer: $\displaystyle \iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}$

28. Evaluate $\displaystyle \iint_S (x^2 + y^2 + z^2) \, dS,$ where $S$ is the portion of plane that lies inside cylinder $x^2 + y^2 = 1$.

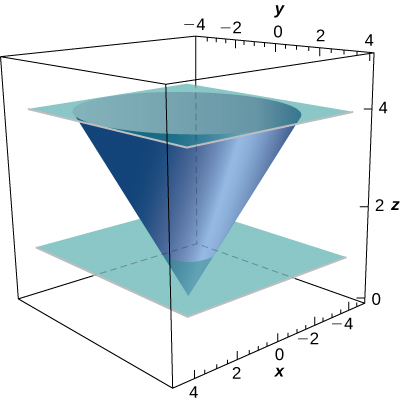
29. [T] Evaluate $\displaystyle \iint_S x^2 z \, dS,$ where $S$ is the portion of cone $z^2 = x^2 + y^2$ that lies between planes $z = 1$ and $z = 4$.

$A diagram of the given upward opening cone in three dimensions. The cone is cut by planes z=1 and z=4.$

Answer: $\text{div}\,\vecs F = a + b$

$\displaystyle \iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}$

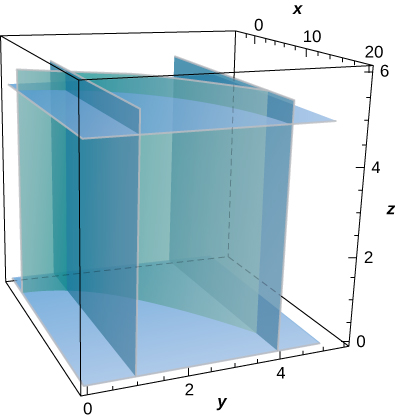
30. [T] Evaluate $\displaystyle \iint_S \frac{xz}{y} \, dS,$ where $S$ is the portion of cylinder $x = y^2$ that lies in the first octant between planes $z = 0, \, z = 5$, and $y = 4$.

$A diagram of the given cylinder in three-dimensions. It is cut by the planes z=0, z=5, y=1, and y=4.$

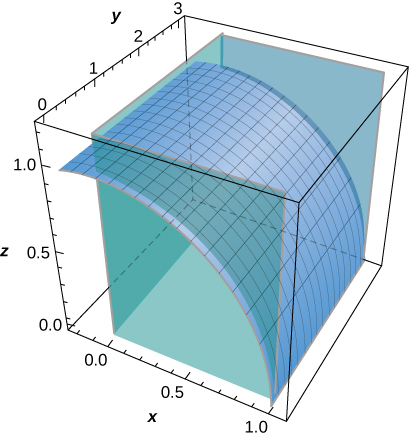
31. [T] Evaluate $\displaystyle \iint_S (z + y) \, dS,$ where $S$ is the part of the graph of $ z = \sqrt{1 - x^2}$ in the first octant between the $xy$-plane and plane $y = 3$.

$A diagram of the given surface in three dimensions in the first octant between the xz-plane and plane y=3. The given graph of z= the square root of (1-x^2) stretches down in a concave down curve from along (0,y,1) to along (1,y,0). It looks like a portion of a horizontal cylinder with base along the xz-plane and height along the y axis.$

Answer: $\displaystyle \iint_S (z + y) \, dS \approx 10.1$

32. Evaluate $\displaystyle \iint_S xyz\, dS$ if $S$ is the part of plane $z = x + y$ that lies over the triangular region in the $xy$-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).

33. Find the mass of a lamina of density $\xi (x,y,z) = z$ in the shape of hemisphere $z = (a^2 - x^2 - y^2)^{1/2}$.

Answer: $m = \pi a^3$

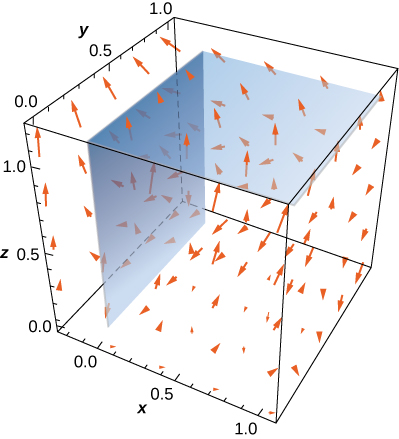
34. Compute $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ where $\vecs F(x,y,z) = x\,\mathbf{\hat i} - 5y\,\mathbf{\hat j} + 4z\,\mathbf{\hat k}$ and $\vecs N$ is an outward normal vector $S,$ where $S$ is the union of two squares $S_1$ : $x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ and $S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1$.

$A diagram in three dimensions. It shows the square formed by the components x=0, 0 <= y <= 1, and 0 <= z <= 1. It also shows the square formed by the components z=1, 0 <= x <= 1, and 0 <= y <= 1.$

35. Compute $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ where $\vecs F(x,y,z) = xy\,\mathbf{\hat i} + z\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}$ and $\vecs N$ is an outward normal vector $S,$ where $S$ is the triangular region cut off from plane $x + y + z = 1$ by the positive coordinate axes.

Answer: $\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{13}{24}$

36. Compute $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ where $\vecs F(x,y,z) = 2yz\,\mathbf{\hat i} + (\tan^{-1}xz)\,\mathbf{\hat j} + e^{xy}\,\mathbf{\hat k}$ and $\vecs N$ is an outward normal vector $S,$ where $S$ is the surface of sphere $x^2 + y^2 + z^2 = 1$.

37. Compute $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ where $\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + xyz\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}$ and $\vecs N$ is an outward normal vector $S,$ where $S$ is the surface of the five faces of the unit cube $0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ missing $z = 0$.

Answer: $\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{3}{4}$

For exercises 38 - 39, express the surface integral as an iterated double integral by using a projection on $S$ on the $yz$-plane.

38. $\displaystyle \iint_S xy^2 z^3 \, dS;$ $S$ is the first-octant portion of plane $2x + 3y + 4z = 12$.

39. $\displaystyle \iint_S (x^2 - 2y + z) \, dS;$ $S$ is the portion of the graph of $4x + y = 8$ bounded by the coordinate planes and plane $z = 6$.

Answer: $\displaystyle \int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz \, dy$

For exercises 40 - 41, express the surface integral as an iterated double integral by using a projection on $S$ on the $xz$-plane.

40. $\displaystyle \iint_S xy^2z^3 \, dS;$ $S$ is the first-octant portion of plane $2x + 3y + 4z = 12$.

41. $\displaystyle \iint_S (x^2 - 2y + z) \, dS;$ is the portion of the graph of $4x + y = 8$ bounded by the coordinate planes and plane $z = 6$.

Answer: $\displaystyle \int_0^2 \int_0^6 \big[x^2 - 2 (8 - 4x) + z\big] \sqrt{17} \, dz \, dx$

42. Evaluate surface integral $\displaystyle \iint_S yz \, dS,$ where $S$ is the first-octant part of plane $x + y + z = \lambda$, where $\lambda$ is a positive constant.

43. Evaluate surface integral $\displaystyle \iint_S (x^2 z + y^2 z) \, dS,$ where $S$ is hemisphere $x^2 + y^2 + z^2 = a^2, \, z \geq 0.$

Answer: $\displaystyle \iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}$

44. Evaluate surface integral $\displaystyle \iint_S z \, dA,$ where $S$ is surface $z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2$.

45. Evaluate surface integral $\displaystyle \iint_S x^2 yz \, dS,$ where $S$ is the part of plane $z = 1 + 2x + 3y$ that lies above rectangle $0 \leq x \leq 3$ and $0 \leq y \leq 2$.

Answer: $\displaystyle \iint_S x^2 yz \, dS = 171 \sqrt{14}$

46. Evaluate surface integral $\displaystyle \iint_S yz \, dS,$ where $S$ is plane $x + y + z = 1$ that lies in the first octant.

47. Evaluate surface integral $\displaystyle \iint_S yz \, dS,$ where $S$ is the part of plane $z = y + 3$ that lies inside cylinder $x^2 + y^2 = 1$.

Answer: $\displaystyle \iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}$

For exercises 48 - 50, use geometric reasoning to evaluate the given surface integrals.

48. $\displaystyle \iint_S \sqrt{x^2 + y^2 + z^2} \, dS,$ where $S$ is surface $x^2 + y^2 + z^2 = 4, \, z \geq 0$

49. $\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS,$ where $S$ is surface $x^2 + y^2 = 4, \, 1 \leq z \leq 3$, oriented with unit normal vectors pointing outward

Answer: $\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS = 16 \pi$

50. $\displaystyle \iint_S (z\,\mathbf{\hat k}) \cdot dS,$ where $S$ is disc $x^2 + y^2 \leq 9$ on plane $z = 4$ oriented with unit normal vectors pointing upward

51. A lamina has the shape of a portion of sphere $x^2 + y^2 + z^2 = a^2$ that lies within cone $z = \sqrt{x^2 + y^2}$. Let $S$ be the spherical shell centered at the origin with radius a, and let $C$ be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the $z$-axis. Determine the mass of the lamina if $\delta(x,y,z) = x^2 y^2 z$.

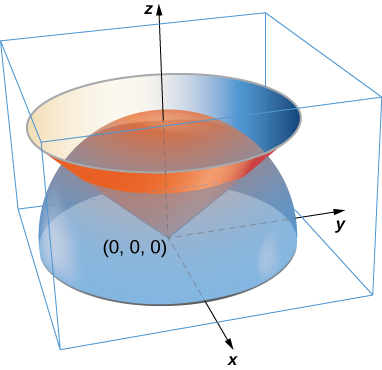
$A diagram in three dimensions. A cone opens upward with point at the origin and an asic of symmetry that coincides with the z-axis. The upper half of a hemisphere with center at the origin opens downward and is cut off by the xy-plane.$

Answer: $m = \dfrac{\pi a^7}{192}$

52. A lamina has the shape of a portion of sphere $x^2 + y^2 + z^2 = a^2$ that lies within cone $z = \sqrt{x^2 + y^2}$. Let $S$ be the spherical shell centered at the origin with radius a, and let $C$ be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is $\phi_0$, with $0 \leq \phi_0 < \dfrac{\pi}{2}$. Determine the mass of that portion of the shape enclosed in the intersection of $S$ and $C.$ Assume $\delta(x,y,z) = x^2y^2z.$

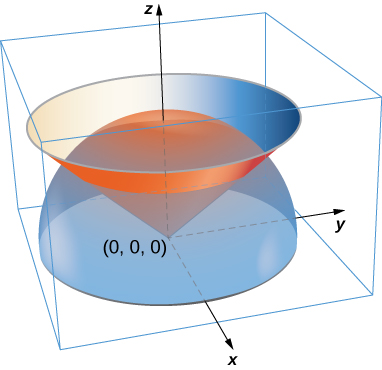
53. A paper cup has the shape of an inverted right circular cone of height 6 in. and radius of top 3 in. If the cup is full of water weighing $62.5 \, lb/ft^3$, find the magnitude of the total force exerted by the water on the inside surface of the cup.

Answer: $F \approx 4.57 \, lb$

For exercises 54 - 55, the heat flow vector field for conducting objects is $\vecs F = - k\vecs\nabla T$, where $T(x,y,z)$ is the temperature in the object and $k > 0$ is a constant that depends on the material. Find the outward flux of $\vecs F$ across the following surfaces $S$ for the given temperature distributions and assume $k = 1$.

54. $T(x,y,z) = 100 e^{-x-y}$; $S$ consists of the faces of cube $|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1$.

55. $T(x,y,z) = - \ln (x^2 + y^2 + z^2)$; $S$ is sphere $x^2 + y^2 + z^2 = a^2$.

Answer: $8\pi a$

For exercises 56 - 57, consider the radial fields $\vecs F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{p/2}} = \dfrac{r}{|r|^p}$, where $p$ is a real number. Let $S$ consist of spheres $A$ and $B$ centered at the origin with radii $0 < a < b$. The total outward flux across $S$ consists of the outward flux across the outer sphere $B$ less the flux into $S$ across inner sphere $A$.

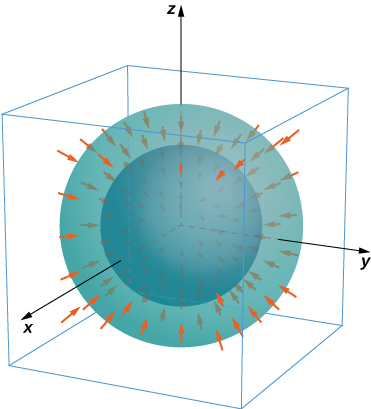
$A diagram in three dimensions of two spheres, one contained completely inside the other. Their centers are both at the origin. Arrows point in toward the origin from outside both spheres.$

56. Find the total flux across $S$ with $p = 0$.

57. Show that for $p = 3$ the flux across $S$ is independent of $a$ and $b.$

Answer: The net flux is zero.

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors