5.3: The Fundamental Theorem of Calculus

Learning Objectives

• Describe the meaning of the Mean Value Theorem for Integrals.
• State the meaning of the Fundamental Theorem of Calculus, Part 1.
• Use the Fundamental Theorem of Calculus, Part 1, to evaluate derivatives of integrals.
• State the meaning of the Fundamental Theorem of Calculus, Part 2.
• Use the Fundamental Theorem of Calculus, Part 2, to evaluate definite integrals.
• Explain the relationship between differentiation and integration.

In the previous two sections, we looked at the definite integral and its relationship to the area under the curve of a function. Unfortunately, so far, the only tools we have available to calculate the value of a definite integral are geometric area formulas and limits of Riemann sums, and both approaches are extremely cumbersome. In this section we look at some more powerful and useful techniques for evaluating definite integrals.

These new techniques rely on the relationship between differentiation and integration. This relationship was discovered and explored by both Sir Isaac Newton and Gottfried Wilhelm Leibniz (among others) during the late 1600s and early 1700s, and it is codified in what we now call the Fundamental Theorem of Calculus, which has two parts that we examine in this section. Its very name indicates how central this theorem is to the entire development of calculus.

Isaac Newton’s contributions to mathematics and physics changed the way we look at the world. The relationships he discovered, codified as Newton’s laws and the law of universal gravitation, are still taught as foundational material in physics today, and his calculus has spawned entire fields of mathematics.

Before we get to this crucial theorem, however, let’s examine another important theorem, the Mean Value Theorem for Integrals, which is needed to prove the Fundamental Theorem of Calculus.

The Mean Value Theorem for Integrals

The Mean Value Theorem for Integrals states that a continuous function on a closed interval takes on its average value at the same point in that interval. The theorem guarantees that if $f(x)$ is continuous, a point $c$ exists in an interval $[a,b]$ such that the value of the function at $c$ is equal to the average value of $f(x)$ over $[a,b]$. We state this theorem mathematically with the help of the formula for the average value of a function that we presented at the end of the preceding section.

The Mean Value Theorem for Integrals, Part 1

If $f(x)$ is continuous over an interval $[a,b]$, then there is at least one point $c∈[a,b]$ such that

$$f(c)=\dfrac{1}{b−a}∫^b_af(x)\,dx.$$

This formula can also be stated as

$$∫^b_af(x)\,dx=f(c)(b−a). \label{meanvaluetheorem}$$

Proof

Since $f(x)$ is continuous on $[a,b]$, by the extreme value theorem (see section on Maxima and Minima), it assumes minimum and maximum values—$m$ and $M$, respectively—on $[a,b]$. Then, for all $x$ in $[a,b]$, we have $m≤f(x)≤M.$ Therefore, by the comparison theorem (see Section on The Definite Integral), we have

$$m(b−a)≤∫^b_af(x)\,dx≤M(b−a).$$

Dividing by $b−a$ gives us

$$m≤\frac{1}{b−a}∫^b_af(x)\,dx≤M.$$

Since $\displaystyle \frac{1}{b−a}∫^b_a f(x)\,dx$ is a number between $m$ and $M$, and since $f(x)$ is continuous and assumes the values $m$ and $M$ over $[a,b]$, by the Intermediate Value Theorem, there is a number $c$ over $[a,b]$ such that

$$f(c)=\frac{1}{b−a}∫^b_a f(x)\,dx,$$

and the proof is complete.□

Average Value Visualization

The graph of a function will be given.  You can change $a$ and $b$ and see the average value for that function between $a$ and $b$.

a = 2.25

b = 6.75

$f(x) = \sqrt{x}$

$f(x) = \sin(x)$

$f(x) = \ln(x)$

$f(x) = \arctan(x)$

$f(x) = x e^{-x^{2}}$

New Function

 

 

Example $\PageIndex{1}$: Finding the Average Value of a Function

Find the average value of the function $f(x)=8−2x$ over the interval $[0,4]$ and find $c$ such that $f(c)$ equals the average value of the function over $[0,4].$

Solution

The formula states the mean value of $f(x)$ is given by

$$\displaystyle \frac{1}{4−0}∫^4_0(8−2x)\,dx. \nonumber$$

We can see in Figure $\PageIndex{1}$ that the function represents a straight line and forms a right triangle bounded by the $x$- and $y$-axes. The area of the triangle is $A=\frac{1}{2}(base)(height).$ We have

$$A=\dfrac{1}{2}(4)(8)=16. \nonumber$$

The average value is found by multiplying the area by $1/(4−0).$ Thus, the average value of the function is

$$\dfrac{1}{4}(16)=4 \nonumber$$

Set the average value equal to $f(c)$ and solve for $c$.

$$\begin{align*} 8−2c =4 \nonumber \\[4pt] c =2 \end{align*}$$

At $c=2,f(2)=4$.

Figure $\PageIndex{1}$: By the Mean Value Theorem, the continuous function $f(x)$ takes on its average value at $c$ at least once over a closed interval.

Exercise $\PageIndex{1}$

Find the average value of the function $f(x)=\dfrac{x}{2}$ over the interval $[0,6]$ and find c such that $f(c)$ equals the average value of the function over $[0,6].$

Hint

Use the procedures from Example $\PageIndex{1}$ to solve the problem

Answer

The average value is $1.5$ and $c=3$.

Example $\PageIndex{2}$: Finding the Point Where a Function Takes on Its Average Value

Given $\displaystyle ∫^3_0x^2\,dx=9$, find $c$ such that $f(c)$ equals the average value of $f(x)=x^2$ over $[0,3]$.

Solution

We are looking for the value of $c$ such that

$$f(c)=\frac{1}{3−0}∫^3_0x^2\,\,dx=\frac{1}{3}(9)=3. \nonumber$$

Replacing $f(c)$ with $c^2$, we have

$$\begin{align*} c^2 &=3 \\[4pt] c &= ±\sqrt{3}. \end{align*}$$

Since $−\sqrt{3}$ is outside the interval, take only the positive value. Thus, $c=\sqrt{3}$ (Figure $\PageIndex{2}$).

Figure $\PageIndex{2}$: Over the interval $[0,3]$, the function $f(x)=x^2$ takes on its average value at $c=\sqrt{3}$.

Exercise $\PageIndex{2}$

Given $\displaystyle ∫^3_0(2x^2−1)\,dx=15$, find $c$ such that $f(c)$ equals the average value of $f(x)=2x^2−1$ over $[0,3]$.

Hint

Use the procedures from Example $\PageIndex{2}$ to solve the problem.

Answer

$c=\sqrt{3}$

Fundamental Theorem of Calculus Part 1: Integrals and Antiderivatives

As mentioned earlier, the Fundamental Theorem of Calculus is an extremely powerful theorem that establishes the relationship between differentiation and integration, and gives us a way to evaluate definite integrals without using Riemann sums or calculating areas. The theorem is comprised of two parts, the first of which, the Fundamental Theorem of Calculus, Part 1, is stated here. Part 1 establishes the relationship between differentiation and integration.

Fundamental Theorem of Calculus, part 1

If $f(x)$ is continuous over an interval $[a,b]$, and the function $F(x)$ is defined by

$$F(x)=∫^x_af(t)\,dt,$$

then $F′(x)=f(x)$ over $[a,b]$.

Before we delve into the proof, a couple of subtleties are worth mentioning here. First, a comment on the notation. Note that we have defined a function, $F(x)$, as the definite integral of another function, $f(t)$, from the point a to the point $x$. At first glance, this is confusing, because we have said several times that a definite integral is a number, and here it looks like it’s a function. The key here is to notice that for any particular value of $x$, the definite integral is a number. So the function $F(x)$ returns a number (the value of the definite integral) for each value of $x$.

Second, it is worth commenting on some of the key implications of this theorem. There is a reason it is called the Fundamental Theorem of Calculus. Not only does it establish a relationship between integration and differentiation, but also it guarantees that any integrable function has an antiderivative. Specifically, it guarantees that any continuous function has an antiderivative.

Proof: Fundamental Theorem of Calculus, Part 1

Applying the definition of the derivative, we have

$$\begin{align*} F′(x) &=\lim_{h→0}\frac{F(x+h)−F(x)}{h} \\[4pt] &=\lim_{h→0}\frac{1}{h} \left[∫^{x+h}_af(t)dt−∫^x_af(t)\,dt \right] \\[4pt] &=\lim_{h→0}\frac{1}{h}\left[∫^{x+h}_af(t)\,dt+∫^a_xf(t)\,dt \right] \\[4pt] &=\lim_{h→0}\frac{1}{h}∫^{x+h}_xf(t)\,dt. \end{align*}$$

Looking carefully at this last expression, we see $\displaystyle \frac{1}{h}∫^{x+h}_x f(t)\,dt$ is just the average value of the function $f(x)$ over the interval $[x,x+h]$. Therefore, by Equation $\ref{meanvaluetheorem}$, there is some number $c$ in $[x,x+h]$ such that

$$\frac{1}{h}∫^{x+h}_x f(t)\,dt=f(c). \nonumber$$

In addition, since $c$ is between $x$ and $h$, $c$ approaches $x$ as $h$ approaches zero. Also, since $f(x)$ is continuous, we have

$$\lim_{h→0}f(c)=\lim_{c→x}f(c)=f(x) \nonumber$$

Putting all these pieces together, we have

$$F′(x)=\lim_{h→0}\frac{1}{h}∫^{x+h}_x f(t)\,dt=\lim_{h→0}f(c)=f(x), \nonumber$$

and the proof is complete.

□

Example $\PageIndex{3}$: Finding a Derivative with the Fundamental Theorem of Calculus

Use the Fundamental Theorem of Calculus, Part 1 to find the derivative of

$$g(x)=∫^x_1\frac{1}{t^3+1}\,dt. \nonumber$$

Solution

According to the Fundamental Theorem of Calculus, the derivative is given by

$$g′(x)=\frac{1}{x^3+1}. \nonumber$$

Exercise $\PageIndex{3}$

Use the Fundamental Theorem of Calculus, Part 1 to find the derivative of $\displaystyle g(r)=∫^r_0\sqrt{x^2+4}\,dx$.

Hint

Follow the procedures from Example $\PageIndex{3}$ to solve the problem.

Answer

$g′(r)=\sqrt{r^2+4}$

Example $\PageIndex{4}$: Using the Fundamental Theorem and the Chain Rule to Calculate Derivatives

Let $\displaystyle F(x)=∫^{\sqrt{x}}_1 \sin t \,dt.$ Find $F′(x)$.

Solution

Letting $u(x)=\sqrt{x}$, we have $\displaystyle F(x)=∫^{u(x)}_1 \sin t \,dt$.

Thus, by the Fundamental Theorem of Calculus and the chain rule,

$$F′(x)=\sin(u(x))\frac{du}{\,dx}=\sin(u(x))⋅\left(\dfrac{1}{2}x^{−1/2}\right)=\dfrac{\sin\sqrt{x}}{2\sqrt{x}}. \nonumber$$

Exercise $\PageIndex{4}$

Let $\displaystyle F(x)=∫^{x^3}_1 \cos t\,dt$. Find $F′(x)$.

Hint

Use the chain rule to solve the problem.

Answer

$F′(x)=3x^2\cos x^3$

Example $\PageIndex{5}$: Using the Fundamental Theorem of Calculus with Two Variable Limits of Integration

Let $\displaystyle F(x)=∫^{2x}_x t^3\,dt$. Find $F′(x)$.

Solution

We have $\displaystyle F(x)=∫^{2x}_x t^3\,dt$. Both limits of integration are variable, so we need to split this into two integrals. We get

$$\begin{align*} F(x) &=∫^{2x}_xt^3\,dt =∫^0_xt^3\,dt+∫^{2x}_0t^3\,dt \\[4pt] &=−∫^x_0t^3\,dt+∫^{2x}_0t^3\,dt. \end{align*}$$

Differentiating the first term, we obtain

$$\frac{d}{\,dx} \left[−∫^x_0t^3\, dt\right]=−x^3 . \nonumber$$

Differentiating the second term, we first let $(x)=2x.$ Then,

$$\begin{align*} \frac{d}{dx} \left[∫^{2x}_0t^3\,dt\right] &=\frac{d}{dx} \left[∫^{u(x)}_0t^3\,dt \right] \\[4pt] &=(u(x))^3\,du\,\,dx \\[4pt] &=(2x)^3⋅2=16x^3.\end{align*}$$

Thus,

$$\begin{align*} F′(x) &=\frac{d}{dx} \left[−∫^x_0t^3\,dt \right]+\frac{d}{dx} \left[∫^{2x}_0t^3\,dt\right] \\[4pt] &=−x^3+16x^3=15x^3 \end{align*}$$

Exercise $\PageIndex{5}$

Let $\displaystyle F(x)=∫^{x^2}_x \cos t \, dt.$ Find $F′(x)$.

Hint

Use the procedures from Example $\PageIndex{5}$ to solve the problem

Answer

$F′(x)=2x\cos x^2−\cos x$

Fundamental Theorem of Calculus, Part 2: The Evaluation Theorem

The Fundamental Theorem of Calculus, Part 2, is perhaps the most important theorem in calculus. After tireless efforts by mathematicians for approximately 500 years, new techniques emerged that provided scientists with the necessary tools to explain many phenomena. Using calculus, astronomers could finally determine distances in space and map planetary orbits. Everyday financial problems such as calculating marginal costs or predicting total profit could now be handled with simplicity and accuracy. Engineers could calculate the bending strength of materials or the three-dimensional motion of objects. Our view of the world was forever changed with calculus.

After finding approximate areas by adding the areas of n rectangles, the application of this theorem is straightforward by comparison. It almost seems too simple that the area of an entire curved region can be calculated by just evaluating an antiderivative at the first and last endpoints of an interval.

The Fundamental Theorem of Calculus, Part 2

If $f(x)$ is continuous over the interval $[a,b]$ and $F(x)$ is any antiderivative of $f(x),$ then

$$∫^b_af(x)\,dx=F(b)−F(a). \label{FTC2}$$

We often see the notation $\displaystyle F(x)|^b_a$ to denote the expression $F(b)−F(a)$. We use this vertical bar and associated limits $a$ and $b$ to indicate that we should evaluate the function $F(x)$ at the upper limit (in this case, $b$), and subtract the value of the function $F(x)$ evaluated at the lower limit (in this case, $a$).

The Fundamental Theorem of Calculus, Part 2 (also known as the evaluation theorem) states that if we can find an antiderivative for the integrand, then we can evaluate the definite integral by evaluating the antiderivative at the endpoints of the interval and subtracting.

Proof

Let $P={x_i},i=0,1,…,n$ be a regular partition of $[a,b].$ Then, we can write

$$\begin{align*} F(b)−F(a) &=F(x_n)−F(x_0) \\[4pt] &=[F(x_n)−F(x_{n−1})]+[F(x_{n−1})−F(x_{n−2})] + … + [F(x_1)−F(x_0)] \\[4pt] &=\sum^n_{i=1}[F(x_i)−F(x_{i−1})]. \end{align*}$$

Now, we know $F$ is an antiderivative of $f$ over $[a,b],$ so by the Mean Value Theorem (see The Mean Value Theorem) for $i=0,1,…,n$ we can find $c_i$ in $[x_{i−1},x_i]$ such that

$$F(x_i)−F(x_{i−1})=F′(c_i)(x_i−x_{i−1})=f(c_i)\,Δx.$$

Then, substituting into the previous equation, we have

$$F(b)−F(a)=\sum_{i=1}^nf(c_i)\,Δx.$$

Taking the limit of both sides as $n→∞,$ we obtain

$$F(b)−F(a)=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=∫^b_af(x)\,dx.$$

□

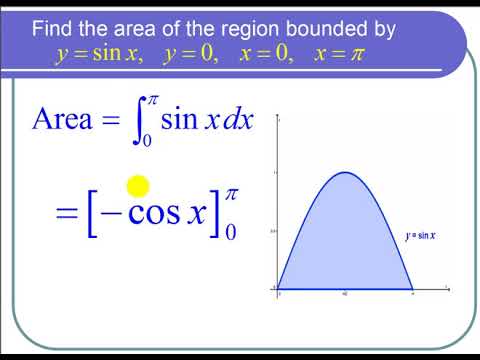
Example $\PageIndex{6}$: Evaluating an Integral with the Fundamental Theorem of Calculus

Use Equation $\ref{FTC2}$ to evaluate

$$∫^2_{−2}(t^2−4)\,dt. \nonumber$$

Solution

Recall the power rule for Antiderivatives:

If $y=x^n$,

$$∫x^n\,dx=\frac{x^{n+1}}{n+1}+C. \nonumber$$

Use this rule to find the antiderivative of the function and then apply the theorem. We have

$$\begin{align*} ∫^2_{−2}(t^2−4)dt &=\left( \frac{t^3}{3}−4t \right)∣^2_{−2} \\[4pt] &=\left[\frac{(2)^3}{3}−4(2)\right]−\left[\frac{(−2)^3}{3}−4(−2)\right] \\[4pt] &=\left[\frac{8}{3}−8\right] − \left[−\frac{8}{3}+8 \right] \\[4pt] &=\frac{8}{3}−8+\frac{8}{3}−8 \\[4pt] &=\frac{16}{3}−16=−\frac{32}{3}.\end{align*}$$

Analysis

Notice that we did not include the “$+ C$” term when we wrote the antiderivative. The reason is that, according to the Fundamental Theorem of Calculus, Part 2 (Equation $\ref{FTC2}$), any antiderivative works. So, for convenience, we chose the antiderivative with $C=0$. If we had chosen another antiderivative, the constant term would have canceled out. This always happens when evaluating a definite integral.

The region of the area we just calculated is depicted in Figure $\PageIndex{3}$. Note that the region between the curve and the $x$-axis is all below the $x$-axis. Area is always positive, but a definite integral can still produce a negative number (a net signed area). For example, if this were a profit function, a negative number indicates the company is operating at a loss over the given interval.

Figure $\PageIndex{3}$: The evaluation of a definite integral can produce a negative value, even though area is always positive.

Example $\PageIndex{7}$: Evaluating a Definite Integral Using the Fundamental Theorem of Calculus, Part 2

Evaluate the following integral using the Fundamental Theorem of Calculus, Part 2 (Equation $\ref{FTC2}$):

$$∫^9_1\frac{x−1}{\sqrt{x}}dx. \nonumber$$

Solution

First, eliminate the radical by rewriting the integral using rational exponents. Then, separate the numerator terms by writing each one over the denominator:

$$∫^9_1\frac{x−1}{x^{1/2}}\,dx=∫^9_1 \left(\frac{x}{x^{1/2}}−\frac{1}{x^{1/2}} \right)\,dx. \nonumber$$

Use the properties of exponents to simplify:

$$∫^9_1 \left(\frac{x}{x^{1/2}}−\frac{1}{x^{1/2}}\right)\,dx=∫^9_1(x^{1/2}−x^{−1/2})\,dx. \nonumber$$

Now, integrate using the power rule:

$$\begin{align*} ∫^9_1(x^{1/2}−x^{−1/2})\,dx &= \left(\frac{x^{3/2}}{\frac{3}{2}}−\frac{x^{1/2}}{\frac{1}{2}}\right)∣^9_1 \\[4pt] &= \left[\frac{(9)^{3/2}}{\frac{3}{2}}−\frac{(9)^{1/2}}{\frac{1}{2}}\right]− \left[\frac{(1)^{3/2}}{\frac{3}{2}}−\frac{(1)^{1/2}}{\frac{1}{2}} \right] \\[4pt] &= \left[\frac{2}{3}(27)−2(3)\right]−\left[\frac{2}{3}(1)−2(1)\right] \\[4pt] &=18−6−\frac{2}{3}+2=\frac{40}{3}. \end{align*}$$

See Figure $\PageIndex{4}$.

Figure $\PageIndex{4}$: The area under the curve from $x=1$ to $x=9$ can be calculated by evaluating a definite integral.

Exercise $\PageIndex{6}$

Use Note to evaluate $\displaystyle ∫^2_1x^{−4}\,dx.$

Hint

Use the power rule.

Answer

$\frac{7}{24}$

Using Calculus to Make a Basket

You are a coach for a basketball team and need to advise your player how fast, in meters per second, the player needs to throw the basketball so that it lands in the basket when the player is a given number of meters away.  The vertical acceleration is 9.8 meters per second squared and the player will release the ball at an angle of $\frac{\pi}{4}$ radians, so that the initial upward velocity will be $\frac{\sqrt{2}}{2}s_0$ meters per second and the horizontal velocity will be a constant $\frac{\sqrt{2}}{2}s_0$ meters per second where $s_0$ is the initial speed of the ball in meters per second.  The basketball hoop is 3 meters high and the player will release the ball when it is 1.8 meters from the ground.  You will be given the horizontal distance $x$ meters from the basket the player will be releasing the ball, and you must instruct the player at what initial speed the ball should be released.  Then you will watch the player shoot the ball and see if the player makes the basket.

   

The horizontal distance from the basket = 3.5 meters.

Initial speed:  s =   

Shoot

Basketball players and Cinematographers:  Alize Reyes Hernandez and Alberto Morales Cesar

 

Example $\PageIndex{8}$: A Roller-Skating Race

James and Kathy are racing on roller skates. They race along a long, straight track, and whoever has gone the farthest after 5 sec wins a prize. If James can skate at a velocity of $f(t)=5+2t$ ft/sec and Kathy can skate at a velocity of $g(t)=10+\cos\left(\frac{π}{2}t\right)$ ft/sec, who is going to win the race?

Solution

We need to integrate both functions over the interval $[0,5]$ and see which value is bigger. For James, we want to calculate

$$∫^5_0(5+2t)\,dt. \nonumber$$

Using the power rule, we have

$$\begin {align*} ∫^5_0(5+2t)\,dt &= \left(5t+t^2\right)∣^5_0 \\[4pt] &=(25+25) \\[4pt] &=50. \end{align*}$$

Thus, James has skated 50 ft after 5 sec. Turning now to Kathy, we want to calculate

$$∫^5_010 + \cos \left(\frac{π}{2}t\right)\, dt. \nonumber$$

We know $\sin t$ is an antiderivative of $\cos t$, so it is reasonable to expect that an antiderivative of $\cos\left(\frac{π}{2}t\right)$ would involve $\sin\left(\frac{π}{2}t\right)$. However, when we differentiate $\sin \left(π^2t\right)$, we get $π^2 \cos\left(π^2t\right)$ as a result of the chain rule, so we have to account for this additional coefficient when we integrate. We obtain

$$\begin{align*} ∫^5_010+\cos \left(\frac{π}{2}t\right)\,dt &= \left(10t+\frac{2}{π} \sin \left(\frac{π}{2}t\right)\right)∣^5_0 \\[4pt] &=\left(50+\frac{2}{π}\right)−\left(0−\frac{2}{π} \sin 0\right )≈50.6. \end{align*}$$

Kathy has skated approximately 50.6 ft after 5 sec. Kathy wins, but not by much!

Exercise $\PageIndex{7}$

Suppose James and Kathy have a rematch, but this time the official stops the contest after only 3 sec. Does this change the outcome?

Hint

Change the limits of integration from those in Example $\PageIndex{7}$.

Answer

Kathy still wins, but by a much larger margin: James skates 24 ft in 3 sec, but Kathy skates 29.3634 ft in 3 sec.

A Parachutist in Free Fall

Julie is an avid skydiver with more than 300 jumps under her belt and has mastered the art of making adjustments to her body position in the air to control how fast she falls. If she arches her back and points her belly toward the ground, she reaches a terminal velocity of approximately 120 mph (176 ft/sec). If, instead, she orients her body with her head straight down, she falls faster, reaching a terminal velocity of 150 mph (220 ft/sec).

Figure $\PageIndex{5}$: Skydivers can adjust the velocity of their dive by changing the position of their body during the free fall. (credit: Jeremy T. Lock)

Since Julie will be moving (falling) in a downward direction, we assume the downward direction is positive to simplify our calculations. Julie executes her jumps from an altitude of 12,500 ft. After she exits the aircraft, she immediately starts falling at a velocity given by $v(t)=32t.$

She continues to accelerate according to this velocity function until she reaches terminal velocity. After she reaches terminal velocity, her speed remains constant until she pulls her ripcord and slows down to land.

On her first jump of the day, Julie orients herself in the slower “belly down” position (terminal velocity is 176 ft/sec). Using this information, answer the following questions.

1. How long after she exits the aircraft does Julie reach terminal velocity?
2. Based on your answer to question 1, set up an expression involving one or more integrals that represents the distance Julie falls after 30 sec.
3. If Julie pulls her ripcord at an altitude of 3000 ft, how long does she spend in a free fall?
4. Julie pulls her ripcord at 3000 ft. It takes 5 sec for her parachute to open completely and for her to slow down, during which time she falls another 400 ft. After her canopy is fully open, her speed is reduced to 16 ft/sec. Find the total time Julie spends in the air, from the time she leaves the airplane until the time her feet touch the ground. On Julie’s second jump of the day, she decides she wants to fall a little faster and orients herself in the “head down” position. Her terminal velocity in this position is 220 ft/sec. Answer these questions based on this velocity:
5. How long does it take Julie to reach terminal velocity in this case?
6. Before pulling her ripcord, Julie reorients her body in the “belly down” position so she is not moving quite as fast when her parachute opens. If she begins this maneuver at an altitude of 4000 ft, how long does she spend in a free fall before beginning the reorientation?

Some jumpers wear “wingsuits” (Figure $\PageIndex{6}$). These suits have fabric panels between the arms and legs and allow the wearer to glide around in a free fall, much like a flying squirrel. (Indeed, the suits are sometimes called “flying squirrel suits.”) When wearing these suits, terminal velocity can be reduced to about 30 mph (44 ft/sec), allowing the wearers a much longer time in the air. Wingsuit flyers still use parachutes to land; although the vertical velocities are within the margin of safety, horizontal velocities can exceed 70 mph, much too fast to land safely.

Figure $\PageIndex{6}$: The fabric panels on the arms and legs of a wingsuit work to reduce the vertical velocity of a skydiver’s fall. (credit: Richard Schneider)

Answer the following question based on the velocity in a wingsuit.

7. If Julie dons a wingsuit before her third jump of the day, and she pulls her ripcord at an altitude of 3000 ft, how long does she get to spend gliding around in the air

Key Concepts

• The Mean Value Theorem for Integrals states that for a continuous function over a closed interval, there is a value c such that $f(c)$ equals the average value of the function.
• The Fundamental Theorem of Calculus, Part 1 shows the relationship between the derivative and the integral.
• The Fundamental Theorem of Calculus, Part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The total area under a curve can be found using this formula.

Key Equations

• Mean Value Theorem for Integrals

If $f(x)$ is continuous over an interval $[a,b]$, then there is at least one point $c∈[a,b]$ such that $$f(c)=\frac{1}{b−a}∫^b_af(x)\,dx.\nonumber$$

• Fundamental Theorem of Calculus, Part 1

If $f(x)$ is continuous over an interval $[a,b]$, and the function $F(x)$ is defined by $$F(x)=∫^x_af(t)\,dt,\nonumber$$

then $$F′(x)=f(x).\nonumber$$

• Fundamental Theorem of Calculus, Part 2

If $f$ is continuous over the interval $[a,b]$ and $F(x)$ is any antiderivative of $f(x)$, then $$∫^b_af(x)\,dx=F(b)−F(a).\nonumber$$

Glossary

fundamental theorem of calculus

the theorem, central to the entire development of calculus, that establishes the relationship between differentiation and integration

fundamental theorem of calculus, part 1

uses a definite integral to define an antiderivative of a function

fundamental theorem of calculus, part 2

(also, evaluation theorem) we can evaluate a definite integral by evaluating the antiderivative of the integrand at the endpoints of the interval and subtracting

mean value theorem for integrals

guarantees that a point $c$ exists such that $f(c)$ is equal to the average value of the function

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.