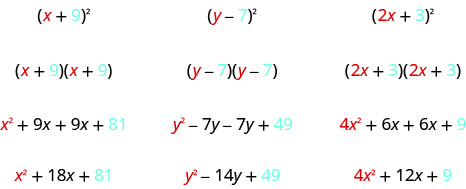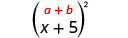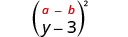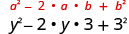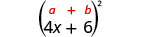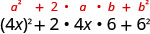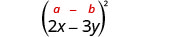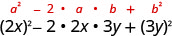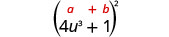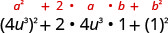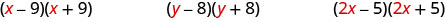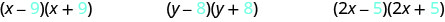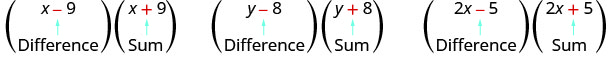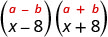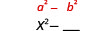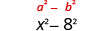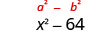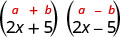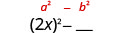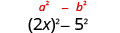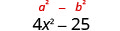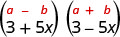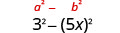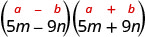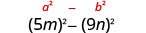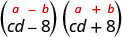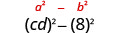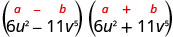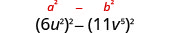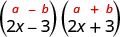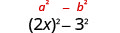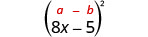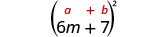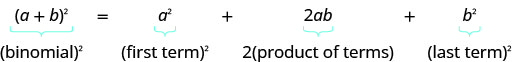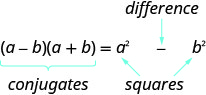Square a Binomial Using the Binomial Squares Pattern
Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials. While you can always get the product by writing the binomial twice and using the methods of the last section, there is less work to do if you learn to use a pattern.
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
Look at these results. Do you see any patterns?
What about the number of terms? In each example we squared a binomial and the result was a trinomial.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
Now look at the first term in each result. Where did it come from?
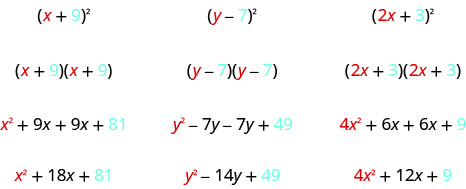
The first term is the product of the first terms of each binomial. Since the binomials are identical, it is just the square of the first term!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
To get the first term of the product, square the first term.
Where did the last term come from? Look at the examples and find the pattern.
The last term is the product of the last terms, which is the square of the last term.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
To get the last term of the product, square the last term.
Finally, look at the middle term. Notice it came from adding the “outer” and the “inner” terms—which are both the same! So the middle term is double the product of the two terms of the binomial.
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
To get the middle term of the product, multiply the terms and double their product.
Putting it all together:
Binomial Square Pattern
If \(a\) and \(b\) are real numbers, the binomial square pattern is
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
Applying this to two binomial types:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
To square a binomial:
- square the first term
- square the last term
- double their product
A number example helps verify the pattern.
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
To multiply \((10+4)^2\) usually you’d follow the Order of Operations.
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
The pattern works!
Try It! \(\PageIndex{1}\)
Multiply: \((x+9)^{2}\)
- Answer
-
\(x^{2}+18 x+81\)
Try It! \(\PageIndex{2}\)
Multiply: \((y+11)^{2}\)
- Answer
-
\(y^{2}+22 y+121\)
Try It! \(\PageIndex{3}\)
Multiply: \((x-9)^{2}\)
- Answer
-
\(x^{2}-18 x+81\)
Try It! \(\PageIndex{4}\)
Multiply: \((p-13)^{2}\)
- Answer
-
\(p^{2}-26 p+169\)
Example \(\PageIndex{3}\)
Multiply: \((4 x+6)^{2}\)
Solution:
| |
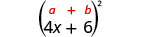 |
| Use the pattern. |
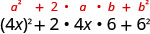 |
| Simplify. |
\(16 x^{2}+48 x+36\) |
Try It! \(\PageIndex{5}\)
Multiply: \((6 x+3)^{2}\)
- Answer
-
\(36 x^{2}+36 x+9\)
Try It! \(\PageIndex{6}\)
Multiply: \((4 x+9)^{2}\)
- Answer
-
\(16 x^{2}+72 x+81\)
Example \(\PageIndex{4}\)
Multiply:\((2 x-3 y)^{2}\)
Solution:
| |
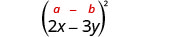 |
| Use the pattern. |
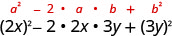 |
| Simplify. |
\(4 x^{2}-12 x y+9 y^{2}\) |
Try It! \(\PageIndex{7}\)
Multiply: \((2 c-d)^{2}\)
- Answer
-
\(4 c^{2}-4 c d+d^{2}\)
Try It! \(\PageIndex{8}\)
Multiply: \((4 x-5 y)^{2}\)
- Answer
-
\(16 x^{2}-40 x y+25 y^{2}\)
Example \(\PageIndex{5}\)
Multiply: \(\left(4 u^{3}+1\right)^{2}\)
Solution:
| |
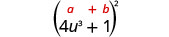 |
| Use the pattern. |
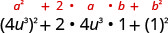 |
| Simplify. |
\(16 u^{6}+8 u^{3}+1\) |
Try It! \(\PageIndex{9}\)
Multiply: \(\left(2 x^{2}+1\right)^{2}\)
- Answer
-
\(4 x^{4}+4 x^{2}+1\)
Try It! \(\PageIndex{10}\)
Multiply: \(\left(3 y^{3}+2\right)^{2}\)
- Answer
-
\(9 y^{6}+12 y^{3}+4\)
Multiply Conjugates Using the Product of Conjugates Pattern
We just saw a pattern for squaring binomials that we can use to make multiplying some binomials easier. Similarly, there is a pattern for another product of binomials. But before we get to it, we need to introduce some vocabulary.
What do you notice about these pairs of binomials?
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
Look at the first term of each binomial in each pair.
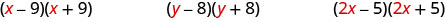
Notice the first terms are the same in each pair.
Look at the last terms of each binomial in each pair.
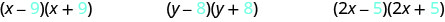
Notice the last terms are the same in each pair.
Notice how each pair has one sum and one difference.
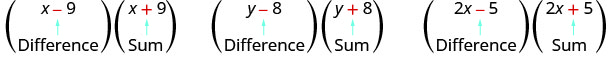
A pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference has a special name. It is called a conjugate pair and is of the form (a−b),(a+b).
Definition: Conjugate Pair
A conjugate pair is two binomials of the form
\[(a-b),(a+b)\nonumber \]
The pair of binomials each have the same first term and the same last term, but one binomial is a sum and the other is a difference.
There is a nice pattern for finding the product of conjugates. You could, of course, simply FOIL to get the product, but using the pattern makes your work easier.
Let’s look for the pattern by using FOIL to multiply some conjugate pairs.
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
Each first term is the product of the first terms of the binomials, and since they are identical it is the square of the first term.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
The last term came from multiplying the last terms, the square of the last term.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
What do you observe about the products?
The product of the two binomials is also a binomial! Most of the products resulting from FOIL have been trinomials.
Why is there no middle term? Notice the two middle terms you get from FOIL combine to 0 in every case, the result of one addition and one subtraction.
The product of conjugates is always of the form \(a^2-b^2\). This is called a difference of squares.
This leads to the pattern:
PRODUCT OF CONJUGATES PATTERN
If \(a\) and \(b\) are real numbers,

The product is called a difference of squares.
To multiply conjugates, square the first term, square the last term, and write the product as a difference of squares.
Let’s test this pattern with a numerical example.
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
Notice, the result is the same!
Example \(\PageIndex{6}\)
Multiply: \((x-8)(x+8)\)
Solution:
First, recognize this as a product of conjugates. The binomials have the same first terms, and the same last terms, and one binomial is a sum and the other is a difference.
| It fits the pattern. |
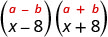 |
| Square the first term, x. |
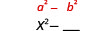 |
| Square the last term, 8. |
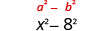 |
| The product is a difference of squares. |
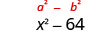 |
Try It! \(\PageIndex{11}\)
Multiply: \((x-5)(x+5)\)
- Answer
-
\(x^{2}-25\)
Try It! \(\PageIndex{12}\)
Multiply: \((w-3)(w+3)\)
- Answer
-
\(w^{2}-9\)
Example \(\PageIndex{7}\)
Multiply: \((2 x+5)(2 x-5)\)
Solution:
Are the binomials conjugates?
| It is the product of conjugates. |
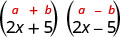 |
| Square the first term, 2x. |
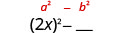 |
| Square the last term, 5. |
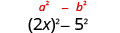 |
| Simplify. The product is a difference of squares. |
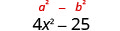 |
Try It! \(\PageIndex{13}\)
Multiply: \((6 x+5)(6 x-5)\)
- Answer
-
\(36 x^{2}-25\)
Try It! \(\PageIndex{14}\)
Multiply: \((2 x+7)(2 x-7)\)
- Answer
-
\(4 x^{2}-49\)
The binomials in the next example may look backwards – the variable is in the second term. But the two binomials are still conjugates, so we use the same pattern to multiply them.
Example \(\PageIndex{8}\)
Find the product:\((3+5 x)(3-5 x)\)
Solution:
| It is the product of conjugates. |
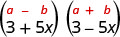 |
| Use the pattern. |
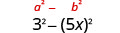 |
| Simplify. |
\(9-25 x^{2}\) |
Try It! \(\PageIndex{15}\)
Multiply: \((7+4 x)(7-4 x)\)
- Answer
-
\(49-16 x^{2}\)
Try It! \(\PageIndex{16}\)
Multiply: \((9-2 y)(9+2 y)\)
- Answer
-
\(81-4 y^{2}\)
Now we’ll multiply conjugates that have two variables.
Example \(\PageIndex{9}\)
Find the product: \((5 m-9 n)(5 m+9 n)\)
Solution:
| This fits the pattern. |
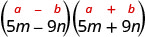 |
| Use the pattern. |
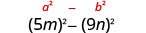 |
| Simplify. |
\(25 m^{2}-81 n^{2}\) |
Try It! \(\PageIndex{17}\)
Find the product: \((4 p-7 q)(4 p+7 q)\)
- Answer
-
\(16 p^{2}-49 q^{2}\)
Try It! \(\PageIndex{18}\)
Find the product: \((3 x-y)(3 x+y)\)
- Answer
-
\(9 x^{2}-y^{2}\)
Example \(\PageIndex{10}\)
Find the product: \((c d-8)(c d+8)\)
Solution:
| This fits the pattern. |
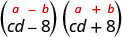 |
| Use the pattern. |
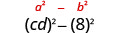 |
| Simplify. |
\(c^{2} d^{2}-64\) |
Try It! \(\PageIndex{19}\)
Find the product: \((x y-6)(x y+6)\)
- Answer
-
\(x^{2} y^{2}-36\)
Try It! \(\PageIndex{20}\)
Find the product: \((a b-9)(a b+9)\)
- Answer
-
\(a^{2} b^{2}-81\)
Example \(\PageIndex{11}\)
Find the product:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
Solution:
| This fits the pattern. |
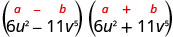 |
| Use the pattern. |
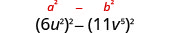 |
| Simplify. |
\(36 u^{4}-121 v^{10}\) |
Try It! \(\PageIndex{21}\)
Find the product:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- Answer
-
\(9 x^{4}-16 y^{6}\)
Try It! \(\PageIndex{22}\)
Find the product:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- Answer
-
\(4 m^{4}-25 n^{6}\)