4.6: Find the Equation of a Line
- Last updated
- May 3, 2019
- Save as PDF
- Page ID
- 18952
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Find an equation of the line given the slope and y-intercept
- Find an equation of the line given the slope and a point
- Find an equation of the line given two points
- Find an equation of a line parallel to a given line
- Find an equation of a line perpendicular to a given line
Note
Before you get started, take this readiness quiz.
- Solve: 23=x5.
If you missed this problem, review Exercise 2.2.4. - Simplify: −25(x−15).
If you missed this problem, review Exercise 1.10.34.
How do online retailers know that ‘you may also like’ a particular item based on something you just ordered? How can economists know how a rise in the minimum wage will affect the unemployment rate? How do medical researchers create drugs to target cancer cells? How can traffic engineers predict the effect on your commuting time of an increase or decrease in gas prices? It’s all mathematics.
You are at an exciting point in your mathematical journey as the mathematics you are studying has interesting applications in the real world.
The physical sciences, social sciences, and the business world are full of situations that can be modeled with linear equations relating two variables. Data is collected and graphed. If the data points appear to form a straight line, an equation of that line can be used to predict the value of one variable based on the value of the other variable.
To create a mathematical model of a linear relation between two variables, we must be able to find the equation of the line. In this section we will look at several ways to write the equation of a line. The specific method we use will be determined by what information we are given.
Find an Equation of the Line Given the Slope and y-Intercept
We can easily determine the slope and intercept of a line if the equation was written in slope–intercept form, y=mx+b. Now, we will do the reverse—we will start with the slope and y-intercept and use them to find the equation of the line.
Example 4.6.1
Find an equation of a line with slope −7 and y-intercept (0,−1).
Solution
Since we are given the slope and y-intercept of the line, we can substitute the needed values into the slope–intercept form, y=mx+b.
| Name the slope. |  |
| Name the y-intercept. | 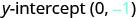 |
| Substitute the values into y=mx+b. | 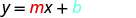 |
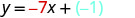 |
|
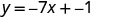 |
Try It 4.6.2
Find an equation of a line with slope 25 and y-intercept (0,4).
- Answer
-
y=25x+4
Try It 4.6.3
Find an equation of a line with slope −1 and y-intercept (0,−3).
- Answer
-
y=−x−3
Sometimes, the slope and intercept need to be determined from the graph.
Example 4.6.4
Find the equation of the line shown.
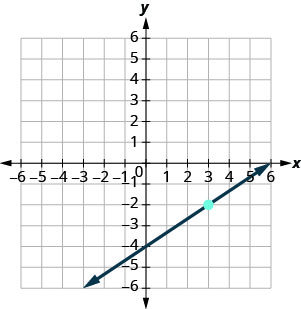
Solution
We need to find the slope and y-intercept of the line from the graph so we can substitute the needed values into the slope–intercept form, y=mx+b.
To find the slope, we choose two points on the graph.
The y-intercept is (0,−4) and the graph passes through (3,−2).
| Find the slope by counting the rise and run. | 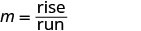 |
 |
|
| Find the y-intercept. | 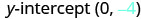 |
| Substitute the values into y=mx+b. | 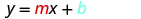 |
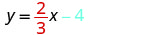 |
Try It 4.6.5
Find the equation of the line shown in the graph.
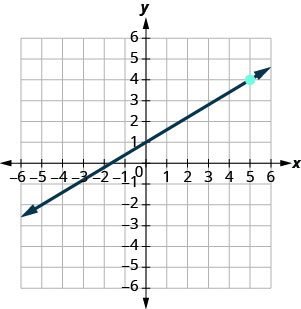
- Answer
-
y=35x+1
Try It 4.6.6
Find the equation of the line shown in the graph.
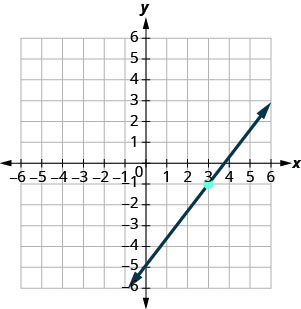
- Answer
-
y=43x−5
Find an Equation of the Line Given the Slope and a Point
Finding an equation of a line using the slope–intercept form of the equation works well when you are given the slope and y-intercept or when you read them off a graph. But what happens when you have another point instead of the y-intercept?
We are going to use the slope formula to derive another form of an equation of the line. Suppose we have a line that has slope mm and that contains some specific point (x1,y1) and some other point, which we will just call (x,y). We can write the slope of this line and then change it to a different form.
m=y−y1x−x1Multiply both sides of the equation by x−x1.m(x−x1)=(y−y1x−x1)(x−x1)Simplify.m(x−x1)=y−y1Rewrite the equation with the y terms on the left.y−y1=m(x−x1)
This format is called the point–slope form of an equation of a line.
POINT–SLOPE FORM OF AN EQUATION OF A LINE
The point–slope form of an equation of a line with slope m and containing the point (x1,y1) is
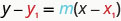
We can use the point–slope form of an equation to find an equation of a line when we are given the slope and one point. Then we will rewrite the equation in slope–intercept form. Most applications of linear equations use the the slope–intercept form.
Example 4.6.7: Find an Equation of a Line Given the Slope and a Point
Find an equation of a line with slope m=25 that contains the point (10,3). Write the equation in slope–intercept form.
Solution




Try It 4.6.8
Find an equation of a line with slope m=56 and containing the point (6,3).
- Answer
-
y=56x−2
Try It 4.6.9
Find an equation of a line with slope m=23 and containing the point (9,2).
- Answer
-
y=23x−4
FIND AN EQUATION OF A LINE GIVEN THE SLOPE AND A POINT.
- Identify the slope.
- Identify the point.
- Substitute the values into the point-slope form, y−y1=m(x−x1).
- Write the equation in slope–intercept form.
Example 4.6.10
Find an equation of a line with slope m=−13 that contains the point (6,−4). Write the equation in slope–intercept form.
Solution
Since we are given a point and the slope of the line, we can substitute the needed values into the point–slope form, y−y1=m(x−x1).
| Identify the slope. | 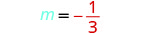 |
| Identify the point. | 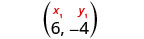 |
| Substitute the values into y−y1=m(x−x1). | 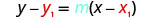 |
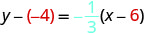 |
|
| Simplify. | 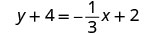 |
| Write in slope–intercept form. | 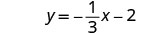 |
Try It 4.6.11
Find an equation of a line with slope m=−25 and containing the point (10,−5).
- Answer
-
y=−25x−1
Try It 4.6.12
Find an equation of a line with slope m=−34, and containing the point (4,−7).
- Answer
-
y=−34x−4
Example 4.6.13
Find an equation of a horizontal line that contains the point (−1,2). Write the equation in slope–intercept form.
Solution
Every horizontal line has slope 0. We can substitute the slope and points into the point–slope form, y−y1=m(x−x1).
| Identify the slope. |  |
| Identify the point. | 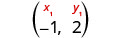 |
| Substitute the values into y−y1=m(x−x1). | 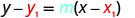 |
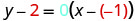 |
|
| Simplify. | 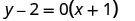 |
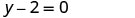 |
|
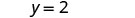 |
|
| Write in slope–intercept form. | It is in y-form, but could be written y=0x+2. |
Try It 4.6.14
Find an equation of a horizontal line containing the point (−3,8).
- Answer
-
y = 8
Try It 4.6.15
Find an equation of a horizontal line containing the point (−1,4).
- Answer
-
y = 4
Find an Equation of the Line Given Two Points
When real-world data is collected, a linear model can be created from two data points. In the next example we’ll see how to find an equation of a line when just two points are given.
We have two options so far for finding an equation of a line: slope–intercept or point–slope. Since we will know two points, it will make more sense to use the point–slope form.
But then we need the slope. Can we find the slope with just two points? Yes. Then, once we have the slope, we can use it and one of the given points to find the equation.
Example 4.6.16: Find an Equation of a Line Given Two Points
Find an equation of a line that contains the points (5,4) and (3,6). Write the equation in slope–intercept form.
Solution




Use the point (3,6) and see that you get the same equation.
Try It 4.6.17
Find an equation of a line containing the points (3,1) and (5,6).
- Answer
-
y=52x−132
Try It 4.6.18
Find an equation of a line containing the points (1,4) and (6,2).
- Answer
-
y=−25x+225
FIND AN EQUATION OF A LINE GIVEN TWO POINTS.
- Find the slope using the given points.
- Choose one point.
- Substitute the values into the point-slope form, y−y1=m(x−x1).
- Write the equation in slope–intercept form.
Example 4.6.19
Find an equation of a line that contains the points (−3,−1) and (2,−2). Write the equation in slope–intercept form.
Solution
Since we have two points, we will find an equation of the line using the point–slope form. The first step will be to find the slope.
| Find the slope of the line through (−3, −1) and (2, −2). | 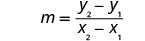 |
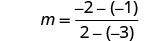 |
|
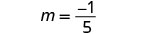 |
|
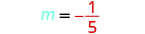 |
|
| Choose either point. | 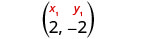 |
| Substitute the values into y−y1=m(x−x1). | 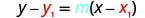 |
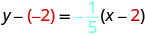 |
|
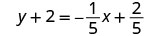 |
|
| Write in slope–intercept form. | 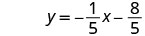 |
Try It 4.6.20
Find an equation of a line containing the points (−2,−4) and (1,−3).
- Answer
-
y=13x−103
Try It 4.6.21
Find an equation of a line containing the points (−4,−3) and (1,−5).
- Answer
-
y=−25x−235
Example 4.6.22
Find an equation of a line that contains the points (−2,4) and (−2,−3). Write the equation in slope–intercept form.
Solution
Again, the first step will be to find the slope.
Find the slope of the line through (−2,4) and (−2,−3)m=y2−x1x2−x1m=−3−4−2−(−2)m=−70 The slope is undefined.
This tells us it is a vertical line. Both of our points have an x-coordinate of −2. So our equation of the line is x=−2. Since there is no yy, we cannot write it in slope–intercept form.
You may want to sketch a graph using the two given points. Does the graph agree with our conclusion that this is a vertical line?
Try It 4.6.23
Find an equation of a line containing the points (5,1) and (5,−4).
- Answer
-
x = 5
Try It 4.6.24
Find an equation of a line containing the points (−4,4) and (−4,3).
- Answer
-
x=−4
We have seen that we can use either the slope–intercept form or the point–slope form to find an equation of a line. Which form we use will depend on the information we are given. This is summarized in Table 4.6.1.
| To Write an Equation of a Line | ||
| If given: | Use: | Form: |
| Slope and y-intercept | slope–intercept | y=mx+b |
| Slope and a point | point–slope | y−y1=m(x−x1) |
| Two points | point–slope | y−y1=m(x−x1) |
Find an Equation of a Line Parallel to a Given Line
Suppose we need to find an equation of a line that passes through a specific point and is parallel to a given line. We can use the fact that parallel lines have the same slope. So we will have a point and the slope—just what we need to use the point–slope equation.
First let’s look at this graphically.
The graph shows the graph of y=2x−3. We want to graph a line parallel to this line and passing through the point (−2,1).
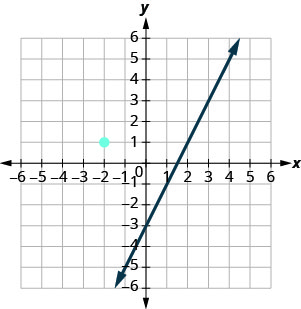
We know that parallel lines have the same slope. So the second line will have the same slope as y=2x−3. That slope is m‖. We’ll use the notation m_{\|} to represent the slope of a line parallel to a line with slope m. (Notice that the subscript ∥ looks like two parallel lines.)
The second line will pass through (−2,1) and have m=2. To graph the line, we start at (−2,1) and count out the rise and run. With m=2 (or m=\frac{2}{1}), we count out the rise 2 and the run 1. We draw the line.
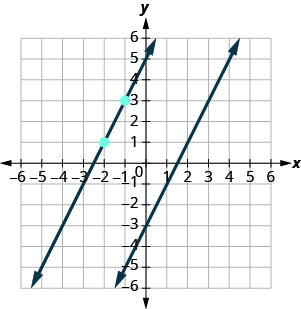
Do the lines appear parallel? Does the second line pass through (−2,1)?
Now, let’s see how to do this algebraically.
We can use either the slope–intercept form or the point–slope form to find an equation of a line. Here we know one point and can find the slope. So we will use the point–slope form.
Example \PageIndex{25}: How to Find an Equation of a Line Parallel to a Given Line
Find an equation of a line parallel to y=2x−3 that contains the point (−2,1). Write the equation in slope–intercept form.
Solution
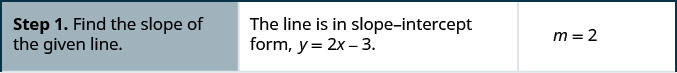




Does this equation make sense? What is the y-intercept of the line? What is the slope?
Try It \PageIndex{26}
Find an equation of a line parallel to the line y=3x+1 that contains the point (4,2). Write the equation in slope–intercept form.
- Answer
-
y=3x−10
Try It \PageIndex{27}
Find an equation of a line parallel to the line y=\frac{1}{2}x−3 that contains the point (6,4).
- Answer
-
y=\frac{1}{2}x+1
FIND AN EQUATION OF A LINE PARALLEL TO A GIVEN LINE.
- Find the slope of the given line.
- Find the slope of the parallel line.
- Identify the point.
- Substitute the values into the point–slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope–intercept form.
Find an Equation of a Line Perpendicular to a Given Line
Now, let’s consider perpendicular lines. Suppose we need to find a line passing through a specific point and which is perpendicular to a given line. We can use the fact that perpendicular lines have slopes that are negative reciprocals. We will again use the point–slope equation, like we did with parallel lines.
The graph shows the graph of y=2x−3. Now, we want to graph a line perpendicular to this line and passing through (−2,1).

We know that perpendicular lines have slopes that are negative reciprocals. We’ll use the notation m_{\perp} to represent the slope of a line perpendicular to a line with slope m. (Notice that the subscript _{\perp} looks like the right angles made by two perpendicular lines.)
\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}
We now know the perpendicular line will pass through (−2,1) with m_{\perp}=−\frac{1}{2}.
To graph the line, we will start at (−2,1) and count out the rise −1 and the run 2. Then we draw the line.
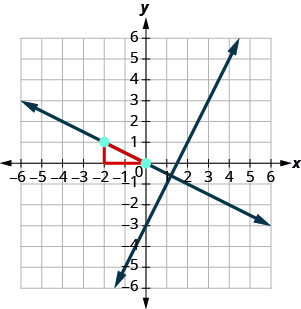
Do the lines appear perpendicular? Does the second line pass through (−2,1)?
Now, let’s see how to do this algebraically. We can use either the slope–intercept form or the point–slope form to find an equation of a line. In this example we know one point, and can find the slope, so we will use the point–slope form.
Example \PageIndex{28}
Find an equation of a line perpendicular to y=2x−3 that contains the point (−2,1). Write the equation in slope–intercept form.
Solution





Try It \PageIndex{29}
Find an equation of a line perpendicular to the line y=3x+1 that contains the point (4,2). Write the equation in slope–intercept form.
- Answer
-
y=−\frac{1}{3}x+\frac{10}{3}
Try It \PageIndex{30}
Find an equation of a line perpendicular to the line y=\frac{1}{2}x−3 that contains the point (6,4).
- Answer
-
y=−2x+16
FIND AN EQUATION OF A LINE PERPENDICULAR TO A GIVEN LINE.
- Find the slope of the given line.
- Find the slope of the perpendicular line.
- Identify the point.
- Substitute the values into the point–slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope–intercept form.
Example \PageIndex{31}
Find an equation of a line perpendicular to x=5 that contains the point (3,−2). Write the equation in slope–intercept form.
Solution
Again, since we know one point, the point–slope option seems more promising than the slope–intercept option. We need the slope to use this form, and we know the new line will be perpendicular to x=5. This line is vertical, so its perpendicular will be horizontal. This tells us the m_{\perp}=0.
\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}
Sketch the graph of both lines. Do they appear to be perpendicular?
Try It \PageIndex{32}
Find an equation of a line that is perpendicular to the line x=4 that contains the point (4,−5). Write the equation in slope–intercept form.
- Answer
-
y=−5
Try It \PageIndex{33}
Find an equation of a line that is perpendicular to the line x=2 that contains the point (2,−1). Write the equation in slope–intercept form.
- Answer
-
y=−1
In Example \PageIndex{31}, we used the point–slope form to find the equation. We could have looked at this in a different way.
We want to find a line that is perpendicular to x=5 that contains the point (3,−2). The graph shows us the line x=5 and the point (3,−2).
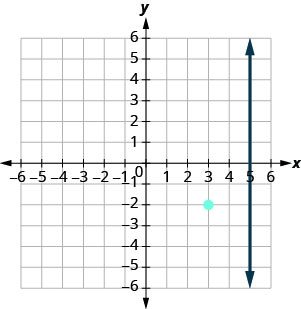
We know every line perpendicular to a vertical line is horizontal, so we will sketch the horizontal line through (3,−2).
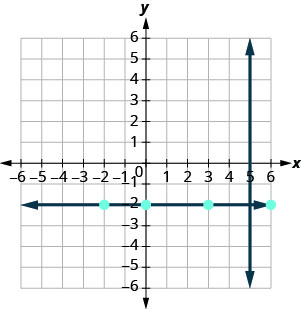
Do the lines appear perpendicular?
If we look at a few points on this horizontal line, we notice they all have y-coordinates of −2. So, the equation of the line perpendicular to the vertical line x=5 is y=−2.
Example \PageIndex{34}
Find an equation of a line that is perpendicular to y=−4 that contains the point (−4,2). Write the equation in slope–intercept form.
Solution
The line y=−4 is a horizontal line. Any line perpendicular to it must be vertical, in the form x=a. Since the perpendicular line is vertical and passes through (−4,2), every point on it has an x-coordinate of −4. The equation of the perpendicular line is x=−4. You may want to sketch the lines. Do they appear perpendicular?
Try It \PageIndex{35}
Find an equation of a line that is perpendicular to the line y=1 that contains the point (−5,1). Write the equation in slope–intercept form.
- Answer
-
x=−5
Try It \PageIndex{36}
Find an equation of a line that is perpendicular to the line y=−5 that contains the point (−4,−5).
- Answer
-
x=−4
Note
Access this online resource for additional instruction and practice with finding the equation of a line.
Key Concepts
- To Find an Equation of a Line Given the Slope and a Point
- Identify the slope.
- Identify the point.
- Substitute the values into the point-slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope-intercept form.
- To Find an Equation of a Line Given Two Points
- Find the slope using the given points.
- Choose one point.
- Substitute the values into the point-slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope-intercept form.
- To Write an Equation of a Line
- If given slope and y-intercept, use slope–intercept form y=mx+b.
- If given slope and a point, use point–slope form y−y_{1}=m(x−x_{1}).
- If given two points, use point–slope form y−y_{1}=m(x−x_{1}).
- To Find an Equation of a Line Parallel to a Given Line
- Find the slope of the given line.
- Find the slope of the parallel line.
- Identify the point.
- Substitute the values into the point-slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope-intercept form.
- To Find an Equation of a Line Perpendicular to a Given Line
- Find the slope of the given line.
- Find the slope of the perpendicular line.
- Identify the point.
- Substitute the values into the point-slope form, y−y_{1}=m(x−x_{1}).
- Write the equation in slope-intercept form.
Glossary
- point–slope form
- The point–slope form of an equation of a line with slope mm and containing the point \left(x_{1}, y_{1}\right) is y-y_{1}=m\left(x-x_{1}\right).


