Skip to main content
Mathematics LibreTexts

1.3: Real Numbers

  1. Last updated
  2. Save as PDF
  • Page ID
    51436

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Learning Objectives

    • Add and subtract real numbers
      • Add real numbers with the same and different signs
      • Subtract real numbers with the same and different signs
      • Simplify combinations that require both addition and subtraction of real numbers.
    • Multiply and divide real numbers
      • Multiply two or more real numbers.
      • Divide real numbers
      • Simplify expressions with both multiplication and division
      • Simplify expressions with real numbers
    • Recognize and combine like terms in an expression
      • Use the order of operations to simplify expressions
    • Simplify compound expressions with real numbers
      • Simplify expressions with fraction bars, brackets, and parentheses
      • Use the distributive property to simplify expressions with grouping symbols
      • Simplify expressions containing absolute values

    Some important terminology to remember before we begin is as follows:

    • integers: counting numbers like 1, 2, 3, etc., including negatives and zero
    • real number: fractions, negative umbers, decimals, integers, and zero are all real numbers
    • absolute value: a number’s distance from zero; it’s always positive. \(|-7| = 7\)
    • sign: this refers to whether a number is positive or negative, we use \(-\) for negative (to the left of zero on the number line)
    • difference: the result of subtraction
    • sum: the result of addition

    The ability to work comfortably with negative numbers is essential to success in algebra. For this reason we will do a quick review of adding, subtracting, multiplying and dividing integers. Integers are all the positive whole numbers, zero, and their opposites (negatives). As this is intended to be a review of integers, the descriptions and examples will not be as detailed as a normal lesson.

    Adding and Subtracting Real Numbers

    When adding integers we have two cases to consider. The first case is whether the signs match (both positive or both negative). If the signs match, we will add the numbers together and keep the sign.

    If the signs don’t match (one positive and one negative number) we will subtract the numbers (as if they were all positive) and then use the sign from the larger number. This means if the larger number is positive, the answer is positive. If the larger number is negative, the answer is negative.

    To add two numbers with the same sign (both positive or both negative)

    • Add their absolute values (without the \(-\) sign)
    • Give the sum the same sign.

    To add two numbers with different signs (one positive and one negative)

    • Find the difference of their absolute values. (Note that when you find the difference of the absolute values, you always subtract the lesser absolute value from the greater one.)
    • Give the sum the same sign as the number with the greater absolute value.

    Example

    Find \(23–73\).

    [reveal-answer q=”951238″]Show Solution[/reveal-answer]
    [hidden-answer a=”951238″]You can’t use your usual method of subtraction because 73 is greater than 23. Rewrite the subtraction as adding the opposite.

    \(23+\left(−73\right)\)

    The addends have different signs, so find the difference of their absolute values.

    \(\begin{array}{c}\left|23\right|=23\,\,\,\text{and}\,\,\,\left|−73\right|=73\\73-23=50\end{array}\)

    Since \(\left|−73\right|>\left|23\right|\), the final answer is negative.

    Answer

    \(23–73=−50\)

    [/hidden-answer]

    Another way to think about subtracting is to think about the distance between the two numbers on the number line. In the example below, \(382\) units, and \(382+93\).

    A number line from negative 93 to 382. Negative 93 is 93 units from 0 and 382 is 382 units from 0. The total distance from negative 93 to 382 can be found by adding them together. 382+93=475 units.

    Example

    Find \(382–\left(−93\right)\).

    [reveal-answer q=”342295″]Show Solution[/reveal-answer]
    [hidden-answer a=”342295″]You are subtracting a negative, so think of this as taking the negative sign away. This becomes an addition problem. \(+93\)

    \(382+93=475\)

    Answer

    \(382–(−93)=475\)

    [/hidden-answer]

    The following video explains how to subtract two signed integers.

    Thumbnail for the embedded element "Ex 2: Subtracting Integers (Two Digit Integers)"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Example

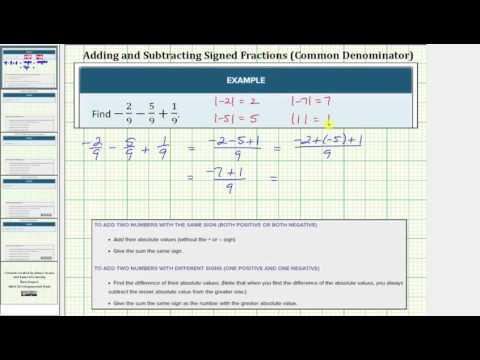
    Find \(-\frac{3}{7}-\frac{6}{7}+\frac{2}{7}\)

    [reveal-answer q=”11416″]Show Solution[/reveal-answer]
    [hidden-answer a=”11416″]Add the first two and give the result a negative sign:

    Since the signs of the first two are the same, find the sum of the absolute values of the fractions

    Since both numbers are negative, the sum is negative. If you owe money, then borrow more, the amount you owe becomes larger.

    \(\left| -\frac{6}{7} \right|=\frac{6}{7}\)

    \(\begin{array}{c}\frac{3}{7}+\frac{6}{7}=\frac{9}{7}\\\\-\frac{3}{7}-\frac{6}{7} =-\frac{9}{7}\end{array}\)

    Now add the third number. The signs are different, so find the difference of their absolute values.

    \(\left| \frac{2}{7} \right|=\frac{2}{7}\)

    \(\frac{9}{7}-\frac{2}{7}=\frac{7}{7}\)

    Since \(-\frac{9}{7}\).

    \(-\frac{9}{7}+\frac{2}{7}=-\frac{7}{7}\)

    Answer

    \(-\frac{3}{7}+\left(-\frac{6}{7}\right)+\frac{2}{7}=-\frac{7}{7}\)

    [/hidden-answer]

    In the following video you will see an example of how to add three fractions with a common denominator that have different signs.

    Thumbnail for the embedded element "Find the Sum and Difference of Three Signed Fractions (Common Denom)"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Example

    Evaluate \(27.832+(−3.06)\). When you add decimals, remember to line up the decimal points so you are adding tenths to tenths, hundredths to hundredths, and so on.

    [reveal-answer q=”545871″]Show Solution[/reveal-answer]
    [hidden-answer a=”545871″]Since the addends have different signs, subtract their absolute values.

    \(\begin{array}{r}\underline{\begin{array}{r}27.832\\-\text{ }3.06\,\,\,\end{array}}\\24.772\end{array}\)

    \(\left|-3.06\right|=3.06\)

    The sum has the same sign as 27.832 whose absolute value is greater.

    Answer

    \(27.832+\left(-3.06\right)=24.772\)

    [/hidden-answer]

    In the following video are examples of adding and subtracting decimals with different signs.

    Thumbnail for the embedded element "Ex: Adding Signed Decimals"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Multiplying and Dividing Real Numbers

    Multiplication and division are inverse operations, just as addition and subtraction are. You may recall that when you divide fractions, you multiply by the reciprocal. Inverse operations “undo” each other.

    Multiply Real Numbers

    Multiplying real numbers is not that different from multiplying whole numbers and positive fractions. However, you haven’t learned what effect a negative sign has on the product.

    With whole numbers, you can think of multiplication as repeated addition. Using the number line, you can make multiple jumps of a given size. For example, the following picture shows the product \(3\cdot4\) as 3 jumps of 4 units each.

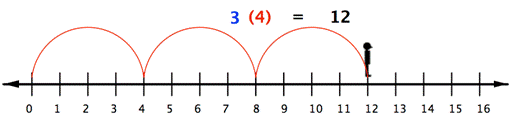
    A number line showing 3 times 4 is 12. From the 0, the right-facing person jumps 4 units at a time, and jumps 3 times. The person lands on 12.

    So to multiply \(3(−4)\), you can face left (toward the negative side) and make three “jumps” forward (in a negative direction).

    A number line representing 3 times negative 4 equals negative 12. A left-facing person jumps left 4 spaces 3 times so that the person lands on negative 12.

    The product of a positive number and a negative number (or a negative and a positive) is negative.

    The Product of a Positive Number and a Negative Number

    To multiply a positive number and a negative number, multiply their absolute values. The product is negative.

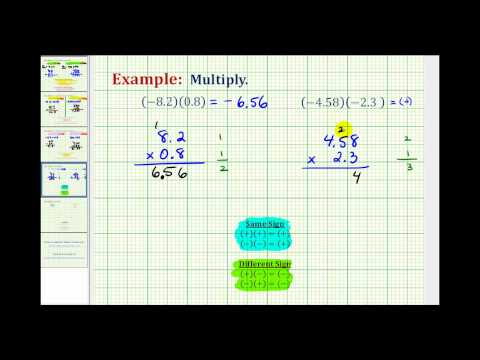
    Example

    Find \(1+1\) or 2 places after the decimal point.

    \(\begin{array}{r}3.8\\\underline{\times\,\,\,0.6}\\2.28\end{array}\)

    The product of a negative and a positive is negative.

    Answer

    \(−3.8(0.6)=−2.28\)

    [/hidden-answer]

    The following video contains examples of how to multiply decimal numbers with different signs.

    Thumbnail for the embedded element "Ex: Multiplying Signed Decimals"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    The Product of Two Numbers with the Same Sign (both positive or both negative)

    To multiply two positive numbers, multiply their absolute values. The product is positive.

    To multiply two negative numbers, multiply their absolute values. The product is positive.

    Example

    Find \(~\left( -\frac{3}{4} \right)\left( -\frac{2}{5} \right)\)

    [reveal-answer q=”322816″]Show Solution[/reveal-answer]
    [hidden-answer a=”322816″]Multiply the absolute values of the numbers. First, multiply the numerators together to get the product’s numerator. Then, multiply the denominators together to get the product’s denominator. Rewrite in lowest terms, if needed.

    \(\left( \frac{3}{4} \right)\left( \frac{2}{5} \right)=\frac{6}{20}=\frac{3}{10}\)

    The product of two negative numbers is positive.

    Answer

    \(\left( -\frac{3}{4} \right)\left( -\frac{2}{5} \right)=\frac{3}{10}\)

    [/hidden-answer]

    The following video shows examples of multiplying two signed fractions, including simplification of the answer.

    Thumbnail for the embedded element "Ex: Multiplying Signed Fractions"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    To summarize:

    • positive \(\cdot\) positive: The product is positive.
    • negative \(\cdot\) negative: The product is positive.
    • negative \(\cdot\) positive: The product is negative.
    • positive \(\cdot\) negative: The product is negative.

    You can see that the product of two negative numbers is a positive number. So, if you are multiplying more than two numbers, you can count the number of negative factors.

    Multiplying More Than Two Negative Numbers

    If there are an even number (0, 2, 4, …) of negative factors to multiply, the product is positive.
    If there are an odd number (1, 3, 5, …) of negative factors, the product is negative.

    Example

    Find \(3(−6)(2)(−3)(−1)\).

    [reveal-answer q=”149062″]Show Solution[/reveal-answer]
    [hidden-answer a=”149062″]Multiply the absolute values of the numbers.

    \(\begin{array}{l}3(6)(2)(3)(1)\\18(2)(3)(1)\\36(3)(1)\\108(1)\\108\end{array}\)

    Count the number of negative factors. There are three \(\left(−6,−3,−1\right)\).

    \(3(−6)(2)(−3)(−1)\)

    Since there are an odd number of negative factors, the product is negative.

    Answer

    \(3(−6)(2)(−3)(−1)=−108\)

    [/hidden-answer]

    The following video contains examples of multiplying more than two signed integers.

    Thumbnail for the embedded element "Ex: Multiplying Three or More Integers"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Divide Real Numbers

    You may remember that when you divided fractions, you multiplied by the reciprocal. Reciprocal is another name for the multiplicative inverse (just as opposite is another name for additive inverse).

    An easy way to find the multiplicative inverse is to just “flip” the numerator and denominator as you did to find the reciprocal. Here are some examples:

    • The reciprocal of \(\frac{9}{4}\)because \(\frac{4}{9}\left(\frac{9}{4}\right)=\frac{36}{36}=1\).
    • The reciprocal of 3 is \(\frac{3}{1}\left(\frac{1}{3}\right)=\frac{3}{3}=1\).
    • The reciprocal of \(\frac{-6}{5}\) because \(-\frac{5}{6}\left( -\frac{6}{5} \right)=\frac{30}{30}=1\).
    • The reciprocal of 1 is 1 as \(1(1)=1\).

    When you divided by positive fractions, you learned to multiply by the reciprocal. You also do this to divide real numbers.

    Think about dividing a bag of 26 marbles into two smaller bags with the same number of marbles in each. You can also say each smaller bag has one half of the marbles.

    \(26\div 2=26\left( \frac{1}{2} \right)=13\)

    Notice that 2 and \(\frac{1}{2}\) are reciprocals.

    Try again, dividing a bag of 36 marbles into smaller bags.

    Number of bags Dividing by number of bags Multiplying by reciprocal
    3 \(36\left( \frac{1}{3} \right)=\frac{36}{3}=\frac{12(3)}{3}=12\)
    4 \(36\left(\frac{1}{4}\right)=\frac{36}{4}=\frac{9\left(4\right)}{4}=9\)
    6 \(36\left(\frac{1}{6}\right)=\frac{36}{6}=\frac{6\left(6\right)}{6}=6\)

    Dividing by a number is the same as multiplying by its reciprocal. (That is, you use the reciprocal of the divisor, the second number in the division problem.)

    Example

    Find \(28\div \frac{4}{3}\)

    [reveal-answer q=”210216″]Show Solution[/reveal-answer]
    [hidden-answer a=”210216″]Rewrite the division as multiplication by the reciprocal. The reciprocal of \(\frac{3}{4}\).

    \(28\div \frac{4}{3}=28\left( \frac{3}{4} \right)\)

    Multiply.

    \(\frac{28}{1}\left(\frac{3}{4}\right)=\frac{28\left(3\right)}{4}=\frac{4\left(7\right)\left(3\right)}{4}=7\left(3\right)=21\)

    Answer

    \(28\div\frac{4}{3}=21\)
    [/hidden-answer]

    Now let’s see what this means when one or more of the numbers is negative. A number and its reciprocal have the same sign. Since division is rewritten as multiplication using the reciprocal of the divisor, and taking the reciprocal doesn’t change any of the signs, division follows the same rules as multiplication.

    Rules of Division

    When dividing, rewrite the problem as multiplication using the reciprocal of the divisor as the second factor.

    When one number is positive and the other is negative, the quotient is negative.

    When both numbers are negative, the quotient is positive.

    When both numbers are positive, the quotient is positive.

    Example

    Find \(24\div\left(-\frac{5}{6}\right)\).

    [reveal-answer q=”716581″]Show Solution[/reveal-answer]
    [hidden-answer a=”716581″]Rewrite the division as multiplication by the reciprocal.

    \(24\div \left( -\frac{5}{6} \right)=24\left( -\frac{6}{5} \right)\)

    Multiply. Since one number is positive and one is negative, the product is negative.

    \(\frac{24}{1}\left( -\frac{6}{5} \right)=-\frac{144}{5}\)

    Answer

    \(24\div \left( -\frac{5}{6} \right)=-\frac{144}{5}\)

    [/hidden-answer]

    Example

    Find \(4\,\left( -\frac{2}{3} \right)\,\div \left( -6 \right)\)

    [reveal-answer q=”557653″]Show Solution[/reveal-answer]
    [hidden-answer a=”557653″]Rewrite the division as multiplication by the reciprocal.

    \(\frac{4}{1}\left( -\frac{2}{3} \right)\left( -\frac{1}{6} \right)\)

    Multiply. There is an even number of negative numbers, so the product is positive.

    \(\frac{4\left(2\right)\left(1\right)}{3\left(6\right)}=\frac{8}{18}\)

    Write the fraction in lowest terms.

    Answer

    \(4\left( -\frac{2}{3} \right)\div \left( -6 \right)=\frac{4}{9}\)

    [/hidden-answer]

    The following video explains how to divide signed fractions.

    Thumbnail for the embedded element "Ex 1: Dividing Signed Fractions"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    traffic-sign-160659

    Remember that a fraction bar also indicates division, so a negative sign in front of a fraction goes with the numerator, the denominator, or the whole fraction: \(-\frac{3}{4}=\frac{-3}{4}=\frac{3}{-4}\).

    In each case, the overall fraction is negative because there’s only one negative in the division.

    The following video explains how to divide signed fractions.

    Thumbnail for the embedded element "Ex 1: Dividing Signed Fractions"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Simplify Expressions With Real Numbers

    Some important terminology before we begin:

    • operations/operators: In mathematics we call things like multiplication, division, addition, and subtraction operations. They are the verbs of the math world, doing work on numbers and variables. The symbols used to denote operations are called operators, such as \(+{, }-{, }\times{, }\div\). As you learn more math, you will learn more operators.
    • term: Examples of terms would be \(-\frac{3}{2}\) or \(a^3\). Even lone integers can be a term, like 0.
    • expression: A mathematical expression is one that connects terms with mathematical operators. For example \(\frac{1}{2}+\left(2^2\right)- 9\div\frac{6}{7}\) is an expression.

    Combining Like Terms

    One way we can simplify expressions is to combine like terms. Like terms are terms where the variables match exactly (exponents included). Examples of like terms would be \(-3xy\) or \(a^2b\) or \(8\). If we have like terms we are allowed to add (or subtract) the numbers in front of the variables, then keep the variables the same. As we combine like terms we need to interpret subtraction signs as part of the following term. This means if we see a subtraction sign, we treat the following term like a negative term. The sign always stays with the term.

    This is shown in the following examples:

    Example

    Combine like terms: \(5x-2y-8x+7y\)
    [reveal-answer q=”730653″]Show Solution[/reveal-answer]
    [hidden-answer a=”730653″]

    The like terms in this expression are:

    \(-8x\)

    \(-7y\)

    Note how we kept the sign in front of each term.

    Combine like terms:

    \(5x-8x = -3x\)

    \(-2y-7y = -9y\)

    Note how signs become operations when you combine like terms.

    Simplified Expression:

    \(5x-2y-8x+7y=-3x-9y\)

    [/hidden-answer]

    In the following video you will be shown how to combine like terms using the idea of the distributive property. Note that this is a different method than is shown in the written examples on this page, but it obtains the same result.

    Thumbnail for the embedded element "Ex 1: Combining Like Terms"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Example

    Combine like terms: \(x^2-3x+9-5x^2+3x-1\)

    [reveal-answer q=”730650″]Show Solution[/reveal-answer]
    [hidden-answer a=”730650″]

    The like terms in this expression are:

    \(-5x^2\)

    \(3x\)

    \(-1\)

    Combine like terms:

    \(\begin{array}{r}x^2-5x^2 = -4x^2\\-3x+3x=0\,\,\,\,\,\,\,\,\,\,\,\\9-1=8\,\,\,\,\,\,\,\,\,\,\,\end{array}\)

    [/hidden-answer]

    In the video that follows, you will be shown another example of combining like terms. Pay attention to why you are not able to combine all three terms in the example.

    Thumbnail for the embedded element "Ex 2: Combining Like Terms"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Order of Operations

    You may or may not recall the order of operations for applying several mathematical operations to one expression. Just as it is a social convention for us to drive on the right-hand side of the road, the order of operations is a set of conventions used to provide order when you are required to use several mathematical operations for one expression. The graphic below depicts the order in which mathematical operations are performed.

    steps of order of operations that say Perform all operations within grouping symbols first. Grouping symbols include {}, [], () Evaluate exponents or square roots Multiply or divide from left to right Add or subtract from left to right
    Order of operations

    Example

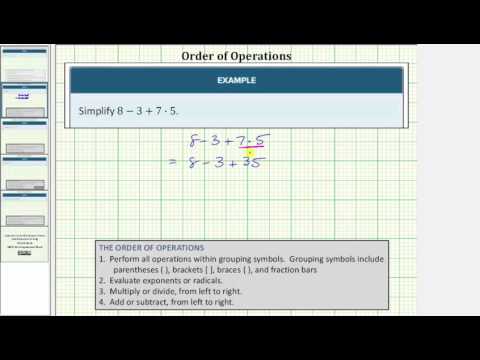
    Simplify \(7–5+3\cdot8\).

    [reveal-answer q=”987816″]Show Solution[/reveal-answer]
    [hidden-answer a=”987816″]According to the order of operations, multiplication comes before addition and subtraction.

    Multiply \(3\cdot8\).

    \(\begin{array}{c}7–5+3\cdot8\\7–5+24\end{array}\)

    Now, add and subtract from left to right. \(7–5\) comes first.

    \(2+24\).

    Finally, add.

    \(2+24=26\)

    Answer

    \(7–5+3\cdot8=26\)

    [/hidden-answer]

    In the following example, you will be shown how to simplify an expression that contains both multiplication and subtraction using the order of operations.

    Thumbnail for the embedded element "Simplify an Expression in the Form: a-b+c*d"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    When you are applying the order of operations to expressions that contain fractions, decimals, and negative numbers, you will need to recall how to do these computations as well.

    Example

    Simplify \(3\cdot\frac{1}{3}-8\div\frac{1}{4}\).

    [reveal-answer q=”265256″]Show Solution[/reveal-answer]
    [hidden-answer a=”265256″]According to the order of operations, multiplication and division come before addition and subtraction. Sometimes it helps to add parentheses to help you know what comes first, so let’s put parentheses around the multiplication and division since it will come before the subtraction.

    \(3\cdot\frac{1}{3}-8\div\frac{1}{4}\)

    Multiply \(3\cdot \frac{1}{3}\) first.

    \(\begin{array}{c}\left(3\cdot\frac{1}{3}\right)-\left(8\div\frac{1}{4}\right)\\\text{}\\=\left(1\right)-\left(8\div \frac{1}{4}\right)\end{array}\)

    Now, divide \(8\div\frac{1}{4}\).

    \(\begin{array}{c}8\div\frac{1}{4}=\frac{8}{1}\cdot\frac{4}{1}=32\\\text{}\\1-32\end{array}\)

    Subtract.

    \(1–32=−31\)

    Answer

    \(3\cdot \frac{1}{3}-8\div \frac{1}{4}=-31\)

    [/hidden-answer]

    In the following video you are shown how to use the order of operations to simplify an expression that contains multiplication, division, and subtraction with terms that contain fractions.

    hqdefault-13.jpg

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Exponents

    When you are evaluating expressions, you will sometimes see exponents used to represent repeated multiplication. Recall that an expression such as \(7\cdot7\). (Exponential notation has two parts: the base and the exponent or the power. In \(7^{2}\), 7 is the base and 2 is the exponent; the exponent determines how many times the base is multiplied by itself.)

    Exponents are a way to represent repeated multiplication; the order of operations places it before any other multiplication, division, subtraction, and addition is performed.

    Example

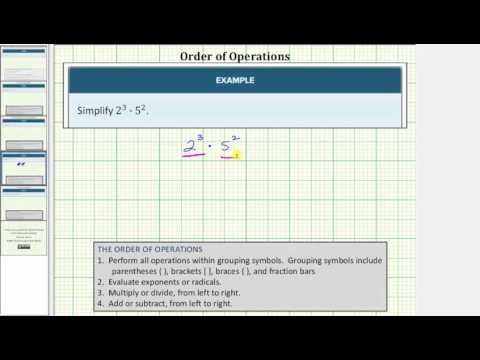
    Simplify \(3^{2}\cdot2^{3}\).

    [reveal-answer q=”360237″]Show Solution[/reveal-answer]
    [hidden-answer a=”360237″]This problem has exponents and multiplication in it. According to the order of operations, simplifying \(2^{3}\) comes before multiplication.

    \(3^{2}\cdot2^{3}\)

    \(3\cdot3\), which equals 9.

    \(9\cdot

    ParseError: EOF expected (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[10]/div/p[5]/span, line 1, column 2
    \)

    \(2\cdot2\cdot2\), which equals 8.

    \(9\cdot 8\)

    Multiply.

    \(9\cdot 8=72\)

    Answer

    \(

    ParseError: EOF expected (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[10]/div/div/p[1]/span[1], line 1, column 2
    \cdot
    ParseError: EOF expected (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[10]/div/div/p[1]/span[2], line 1, column 2
    =72\)

    [/hidden-answer]

    In the video that follows, an expression with exponents on its terms is simplified using the order of operations.

    Thumbnail for the embedded element "Simplify an Expression in the Form: a^n*b^m"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Grouping Symbols

    Grouping symbols such as parentheses ( ), brackets [ ], braces\(\displaystyle \left\{ {} \right\}\), and fraction bars can be used to further control the order of the four arithmetic operations. The rules of the order of operations require computation within grouping symbols to be completed first, even if you are adding or subtracting within the grouping symbols and you have multiplication outside the grouping symbols. After computing within the grouping symbols, divide or multiply from left to right and then subtract or add from left to right. When there are grouping symbols within grouping symbols, calculate from the inside to the outside. That is, begin simplifying within the innermost grouping symbols first.

    Remember that parentheses can also be used to show multiplication. In the example that follows, both uses of parentheses—as a way to represent a group, as well as a way to express multiplication—are shown.

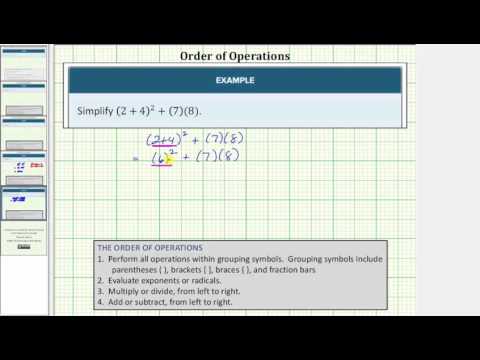
    Example

    Simplify \(\left(3+4\right)^{2}+\left(8\right)\left(4\right)\).

    [reveal-answer q=”548490″]Show Solution[/reveal-answer]
    [hidden-answer a=”548490″]This problem has parentheses, exponents, multiplication, and addition in it. The first set of parentheses is a grouping symbol. The second set indicates multiplication.

    Grouping symbols are handled first. Add numbers in parentheses.

    \(\begin{array}{c}(3+4)^{2}+(8)(4)\\(7)^{2}+(8)(4)\end{array}\)

    Simplify \(7^{2}\).

    \(\begin{array}{c}7^{2}+(8)(4)\\49+(8)(4)\end{array}\)

    Multiply.

    \(\begin{array}{c}49+(8)(4)\\49+(32)\end{array}\)

    Add.

    \(49+32=81\)

    Answer

    \((3+4)^{2}+(8)(4)=81\)

    [/hidden-answer]

    Example

    Simplify \(4\cdot{\frac{3[5+{(2 + 3)}^2]}{2}}\)
    [reveal-answer q=”358226″]Show Solution[/reveal-answer]
    [hidden-answer a=”358226″]

    There are brackets and parentheses in this problem. Compute inside the innermost grouping symbols first.

    \(\begin{array}{c}4\cdot{\frac{3[5+{(2 + 3)}^2]}{2}}\\\text{ }\\=4\cdot{\frac{3[5+{(5)}^2]}{2}}\end{array}\)

    Then apply the exponent

    \(\begin{array}{c}4\cdot{\frac{3[5+{(5)}^2]}{2}}\\\text{}\\=4\cdot{\frac{3[5+25]}{2}}\\\text{ }\\=4\cdot{\frac{3[30]}{2}}\end{array}\)

    Then simplify the fraction

    \(\begin{array}{c}4\cdot{\frac{3[30]}{2}}\\\text{}\\=4\cdot{\frac{90}{2}}\\\text{ }\\=4\cdot{45}\\\text{ }\\=180\end{array}\)

    Answer

    \(4\cdot{\frac{3[5+{(2 + 3)}^2]}{2}}=180\)

    [/hidden-answer]

    In the following video, you are shown how to use the order of operations to simplify an expression with grouping symbols, exponents, multiplication, and addition.

    Thumbnail for the embedded element "Simplify an Expression in the Form: (a+b)^2+c*d"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    Think About It

    These problems are very similar to the examples given above. How are they different and what tools do you need to simplify them?

    a) Simplify \(\left(1.5+3.5\right)–2\left(0.5\cdot6\right)^{2}\). This problem has parentheses, exponents, multiplication, subtraction, and addition in it, as well as decimals instead of integers.

    Use the box below to write down a few thoughts about how you would simplify this expression with decimals and grouping symbols.

    [practice-area rows=”2″][/practice-area]

    [reveal-answer q=”680970″]Show Solution[/reveal-answer]
    [hidden-answer a=”680970″]
    Grouping symbols are handled first. Add numbers in the first set of parentheses.

    \(\begin{array}{c}(1.5+3.5)–2(0.5\cdot6)^{2}\\5–2(0.5\cdot6)^{2}\end{array}\)

    Multiply numbers in the second set of parentheses.

    \(\begin{array}{c}5–2(0.5\cdot6)^{2}\\5–2(3)^{2}\end{array}\)

    Evaluate exponents.

    \(\begin{array}{c}5–2(3)^{2}\\5–2\cdot9\end{array}\)

    Multiply.

    \(\begin{array}{c}5–2\cdot9\\5–18\end{array}\)

    Subtract.

    \(5–18=−13\)

    Answer

    \((1.5+3.5)–2(0.5\cdot6)^{2}=−13\)

    [/hidden-answer]

    b) Simplify \(

    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[11]/div/div/div[3]/div/div[1]/p[3]/span[1], line 1, column 1
    +
    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[11]/div/div/div[3]/div/div[1]/p[3]/span[2], line 1, column 1
    \cdot \,32\).

    Use the box below to write down a few thoughts about how you would simplify this expression with fractions and grouping symbols.

    [practice-area rows=”2″][/practice-area]
    [reveal-answer q=”680972″]Show Solution[/reveal-answer]
    [hidden-answer a=”680972″]
    This problem has exponents, multiplication, and addition in it, as well as fractions instead of integers.

    According to the order of operations, simplify the terms with the exponents first, then multiply, then add.

    \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{4}\right)^{3}\cdot32\)

    Evaluate: \(\left(\frac{1}{2}\right)^{2}=\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\)

    \(\frac{1}{4}+\left(\frac{1}{4}\right)^{3}\cdot32\)

    Evaluate: \(\left(\frac{1}{4}\right)^{3}=\frac{1}{4}\cdot\frac{1}{4}\cdot\frac{1}{4}=\frac{1}{64}\)

    \(\frac{1}{4}+\frac{1}{64}\cdot32\)

    Multiply.

    \(\frac{1}{4}+\frac{32}{64}\)

    Simplify. \(\frac{1}{4}+\frac{1}{2}\).

    \(\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\)

    Answer

    \(

    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[11]/div/div/div[3]/div/div[2]/p/span[1], line 1, column 1
    +
    ParseError: invalid DekiScript (click for details)
    Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/00:_Review/1.03:_Real_Numbers), /content/body/div[11]/div/div/div[3]/div/div[2]/p/span[2], line 1, column 1
    \cdot 32=\frac{3}{4}\)[/hidden-answer]

    Simplify Compound Expressions With Real Numbers

    In this section, we will use the skills from the last section to simplify mathematical expressions that contain many grouping symbols and many operations. We are using the term compound to describe expressions that have many operations and many grouping symbols. More care is needed with these expressions when you apply the order of operations. Additionally, you will see how to handle absolute value terms when you simplify expressions.

    Example

    Simplify \(\frac{5-[3+(2\cdot (-6))]}{{{3}^{2}}+2}\)

    [reveal-answer q=”906386″]Show Solution[/reveal-answer]
    [hidden-answer a=”906386″]This problem has brackets, parentheses, fractions, exponents, multiplication, subtraction, and addition in it.

    Grouping symbols are handled first. The parentheses around the \((2\cdot(−6))\). Begin working out from there. (The fraction line acts as a type of grouping symbol, too; you simplify the numerator and denominator independently, and then divide the numerator by the denominator at the end.)

    \(\begin{array}{c}\frac{5-\left[3+\left(2\cdot\left(-6\right)\right)\right]}{3^{2}+2}\\\\\frac{5-\left[3+\left(-12\right)\right]}{3^{2}+2}\end{array}\)

    Add \(-12\), which are in brackets, to get \(-9\).

    \(\begin{array}{c}\frac{5-\left[3+\left(-12\right)\right]}{3^{2}+2}\\\\\frac{5-\left[-9\right]}{3^{2}+2}\end{array}\)

    Subtract \(5–\left[−9\right]=5+9=14\).

    \(\begin{array}{c}\frac{5-\left[-9\right]}{3^{2}+2}\\\\\frac{14}{3^{2}+2}\end{array}\)

    The top of the fraction is all set, but the bottom (denominator) has remained untouched. Apply the order of operations to that as well. Begin by evaluating \(3^{2}=9\).

    \(\begin{array}{c}\frac{14}{3^{2}+2}\\\\\frac{14}{9+2}\end{array}\)

    Now add. \(9+2=11\).

    \(\begin{array}{c}\frac{14}{9+2}\\\\\frac{14}{11}\end{array}\)

    Answer

    \(\frac{5-\left[3+\left(2\cdot\left(-6\right)\right)\right]}{3^{2}+2}=\frac{14}{11}\)

    [/hidden-answer]

    The video that follows contains an example similar to the written one above. Note how the numerator and denominator of the fraction are simplified separately.

    Thumbnail for the embedded element "Simplify an Expression in Fraction Form"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    The Distributive Property

    Parentheses are used to group or combine expressions and terms in mathematics. You may see them used when you are working with formulas, and when you are translating a real situation into a mathematical problem so you can find a quantitative solution.

    Combo Meal Distributive Property
    Combo Meal Distributive Property

    For example, you are on your way to hang out with your friends, and call them to ask if they want something from your favorite drive-through. Three people want the same combo meal of 2 tacos and one drink. You can use the distributive property to find out how many total tacos and how many total drinks you should take to them.

    \(\begin{array}{c}\,\,\,3\left(2\text{ tacos }+ 1 \text{ drink}\right)\\=3\cdot{2}\text{ tacos }+3\text{ drinks }\\\,\,=6\text{ tacos }+3\text{ drinks }\end{array}\)

    The distributive property allows us to explicitly describe a total that is a result of a group of groups. In the case of the combo meals, we have three groups of ( two tacos plus one drink). The following definition describes how to use the distributive property in general terms.

    The Distributive Property of Multiplication

    For all real numbers a, b, and c, \(a(b+c)=ab+ac\).
    What this means is that when a number multiplies an expression inside parentheses, you can distribute the multiplication to each term of the expression individually.

    To simplify \(3\left(3+y\right)-y+9\), it may help to see the expression translated into words:

    multiply three by (the sum of three and y), then subtract y, then add 9

    To multiply three by the sum of three and y, you use the distributive property –

    \(\begin{array}{c}\,\,\,\,\,\,\,\,\,3\left(3+y\right)-y+9\\\,\,\,\,\,\,\,\,\,=\underbrace{3\cdot{3}}+\underbrace{3\cdot{y}}-y+9\\=9+3y-y+9\end{array}\)

    Now you can subtract y from 3y and add 9 to 9.

    \(\begin{array}{c}9+3y-y+9\\=18+2y\end{array}\)

    The next example shows how to use the distributive property when one of the terms involved is negative.

    Example

    Simplify \(a+2\left(5-a\right)+3\left(a+4\right)\)
    [reveal-answer q=”233674″]Show Solution[/reveal-answer]
    [hidden-answer a=”233674″]

    This expression has two sets of parentheses with variables locked up in them. We will use the distributive property to remove the parentheses.

    \(\begin{array}{c}a+2\left(5-a\right)+3\left(a+4\right)\\=a+2\cdot{5}-2\cdot{a}+3\cdot{a}+3\cdot{4}\end{array}\)

    Note how we placed the negative sign that was on b in front of the 2 when we applied the distributive property. When you multiply a negative by a positive the result is negative, so \(2\cdot{-a}=-2a\). It is important to be careful with negative signs when you are using the distributive property.

    \(\begin{array}{c}a+2\cdot{5}-2\cdot{a}+3\cdot{a}+3\cdot{4}\\=a+10-2a+3a+12\\=2a+22\end{array}\)

    We combined all the terms we could to get our final result.

    Answer

    \(a+2\left(5-a\right)+3\left(a+4\right)=2a+22\)

    [/hidden-answer]

    Absolute Value

    Absolute value expressions are one final method of grouping that you may see. Recall that the absolute value of a quantity is always positive or 0.

    When you see an absolute value expression included within a larger expression, treat the absolute value like a grouping symbol and evaluate the expression within the absolute value sign first. Then take the absolute value of that expression. The example below shows how this is done.

    Example

    Simplify \(\frac{3+\left|2-6\right|}{2\left|3\cdot1.5\right|-\left(-3\right)}\).

    [reveal-answer q=”572632″]Show Solution[/reveal-answer]
    [hidden-answer a=”572632″]This problem has absolute values, decimals, multiplication, subtraction, and addition in it.

    Grouping symbols, including absolute value, are handled first. Simplify the numerator, then the denominator.

    Evaluate \(\left|2–6\right|\).

    \(\begin{array}{c}\frac{3+\left|2-6\right|}{2\left|3\cdot1.5\right|-\left(-3\right)}\\\\\frac{3+\left|-4\right|}{2\left|3\cdot1.5\right|-\left(-3\right)}\end{array}\)

    Take the absolute value of \(\left|−4\right|\).

    \(\begin{array}{c}\frac{3+\left|-4\right|}{2\left|3\cdot1.5\right|-\left(-3\right)}\\\\\frac{3+4}{2\left|3\cdot1.5\right|-\left(-3\right)}\end{array}\)

    Add the numbers in the numerator.

    \(\begin{array}{c}\frac{3+4}{2\left|3\cdot1.5\right|-\left(-3\right)}\\\\\frac{7}{2\left| 3\cdot 1.5 \right|-(-3)}\end{array}\)

    Now that the numerator is simplified, turn to the denominator.

    Evaluate the absolute value expression first. \(3 \cdot 1.5 = 4.5\), giving

    \(\begin{array}{c}\frac{7}{2\left|{3\cdot{1.5}}\right|-(-3)}\\\\\frac{7}{2\left|{ 4.5}\right|-(-3)}\end{array}\)

    The expression “\(2\left|4.5\right|\)” reads “2 times the absolute value of 4.5.” Multiply 2 times 4.5.

    \(\begin{array}{c}\frac{7}{2\left|4.5\right|-\left(-3\right)}\\\\\frac{7}{9-\left(-3\right)}\end{array}\)

    Subtract.

    \(\begin{array}{c}\frac{7}{9-\left(-3\right)}\\\\\frac{7}{12}\end{array}\)

    Answer

    \(\frac{3+\left|2-6\right|}{2\left|3\cdot1.5\right|-3\left(-3\right)}=\frac{7}{12}\)

    [/hidden-answer]

    The following video uses the order of operations to simplify an expression in fraction form that contains absolute value terms. Note how the absolute values are treated like parentheses and brackets when using the order of operations.

    Thumbnail for the embedded element "Simplify an Expression in Fraction Form with Absolute Values"

    A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=36

    CC licensed content, Original
    CC licensed content, Shared previously

    1.3: Real Numbers is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      OER program or Publisher
      Lumen
    2. Tags
      This page has no tags.