1.3: Multi-Step Linear Equations
- Page ID
- 51441
Learning Objectives
- Solve multi-step equations
- Use properties of equality to isolate variables and solve algebraic equations
- Solve equations containing absolute values
- Use the distributive property
- Use the properties of equality and the distributive property to solve equations containing parentheses
- Clear fractions and decimals from equations to make them easier to solve
- Classify solutions to linear equations
- Solve equations that have one solution, no solution, or an infinite number of solutions
- Recognize when a linear equation that contains absolute value does not have a solution
Use properties of equality to isolate variables and solve algebraic equations

There are some equations that you can solve in your head quickly. For example—what is the value of y in the equation \(y=3\). You only needed to do one thing to get the answer: divide 6 by 2.
Other equations are more complicated. Solving \(\displaystyle 4\left( \frac{1}{3}t+\frac{1}{2}\right)=6\) without writing anything down is difficult! That’s because this equation contains not just a variable but also fractions and terms inside parentheses. This is a multi-step equation, one that takes several steps to solve. Although multi-step equations take more time and more operations, they can still be simplified and solved by applying basic algebraic rules.
Remember that you can think of an equation as a balance scale, with the goal being to rewrite the equation so that it is easier to solve but still balanced. The addition property of equality and the multiplication property of equality explain how you can keep the scale, or the equation, balanced. Whenever you perform an operation to one side of the equation, if you perform the same exact operation to the other side, you’ll keep both sides of the equation equal.
If the equation is in the form \(ax+b=c\), where x is the variable, you can solve the equation as before. First “undo” the addition and subtraction, and then “undo” the multiplication and division.
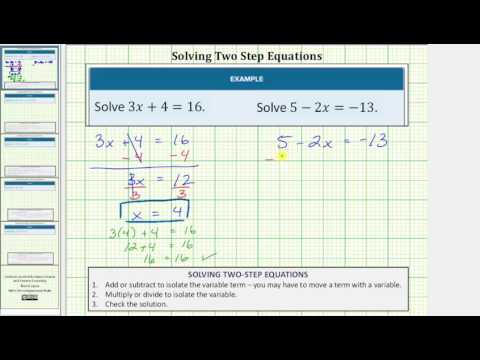
Example
Solve \(3y+2=11\).
[reveal-answer q=”843520″]Show Solution[/reveal-answer]
[hidden-answer a=”843520″]
Subtract 2 from both sides of the equation to get the term with the variable by itself.
\(\displaystyle \begin{array}{r}3y+2\,\,\,=\,\,11\\\underline{\,\,\,\,\,\,\,-2\,\,\,\,\,\,\,\,-2}\\3y\,\,\,\,=\,\,\,\,\,9\end{array}\)
Divide both sides of the equation by 3 to get a coefficient of 1 for the variable.
\(\begin{array}{r}\,\,\,\,\,\,\underline{3y}\,\,\,\,=\,\,\,\,\,\underline{9}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9\\\,\,\,\,\,\,\,\,\,\,y\,\,\,\,=\,\,\,\,3\end{array}\)
Answer
\(y=3\)[/hidden-answer]
In the following video we show examples of solving two step linear equations.
Example
Solve \(3x+5x+4-x+7=88\).
[reveal-answer q=”455516″]Show Solution[/reveal-answer]
[hidden-answer a=”455516″]
There are three like terms \(5x\), and \(–x\) involving a variable. Combine these like terms. 4 and 7 are also like terms and can be added.
\(\begin{array}{r}\,\,3x+5x+4-x+7=\,\,\,88\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7x+4+7=\,\,\,88\end{array}\)
The equation is now in the form \(ax+b=c\), so we can solve as before.
\(7x+11\,\,\,=\,\,\,88\)
Subtract 11 from both sides.
\(\begin{array}{r}7x+11\,\,\,=\,\,\,88\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-11\,\,\,\,\,\,\,-11}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7x\,\,\,=\,\,\,77\end{array}\)
Divide both sides by 7.
\(\begin{array}{r}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{7x}\,\,\,=\,\,\,\underline{77}\\7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,=\,\,\,11\end{array}\)
Answer
\(x=11\)[/hidden-answer]
In the following video, we show an example of solving a linear equation that requires combining like terms.
Some equations may have the variable on both sides of the equal sign, as in this equation: \(4x-6=2x+10\).
To solve this equation, we need to “move” one of the variable terms. This can make it difficult to decide which side to work with. It doesn’t matter which term gets moved, \(2x\), however, to avoid negative coefficients, you can move the smaller term.
Examples
Solve: \(4x-6=2x+10\)
[reveal-answer q=”457216″]Show Solution[/reveal-answer]
[hidden-answer a=”457216″]
Choose the variable term to move—to avoid negative terms choose \(2x\)
\(\,\,\,4x-6=2x+10\\\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x}\\\,\,\,4x-6=10\)
Now add 6 to both sides to isolate the term with the variable.
\(\begin{array}{r}4x-6=10\\\underline{\,\,\,\,+6\,\,\,+6}\\4x=16\end{array}\)
Now divide each side by 4 to isolate the variable x.
\(\begin{array}{c}\frac{4x}{4}=\frac{16}{4}\\\\x=4\end{array}\)
[/hidden-answer]
In this video, we show an example of solving equations that have variables on both sides of hte equal sign.
Solving Multi-Step Equations With Absolute Value
We can apply the same techniques we used for solving a one-step equation which contains absolute value to an equation that will take more than one step to solve. Let’s start with an example where the first step is to write two equations, one equal to positive 26 and one equal to negative 26.
Example
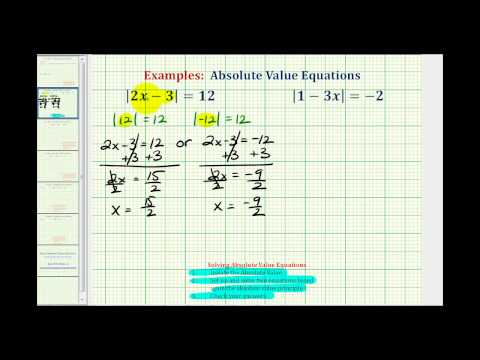
Solve for p. \(\left|2p–4\right|=26\)
[reveal-answer q=”371950″]Show Solution[/reveal-answer]
[hidden-answer a=”371950″]
Write the two equations that will give an absolute value of 26.
\(\displaystyle 2p-4=26\,\,\,\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,2p-4=\,-26\)
Solve each equation for p by isolating the variable.
\(\displaystyle \begin{array}{r}2p-4=26\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2p-4=\,-26\\\underline{\,\,\,\,\,\,+4\,\,\,\,+4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,+4\,\,\,\,\,\,\,+4}\\\underline{2p}\,\,\,\,\,\,=\underline{30}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{2p}\,\,\,\,\,=\,\underline{-22}\\2\,\,\,\,\,\,\,=\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,=\,\,\,\,\,\,\,\,2\\\,\,\,\,\,\,\,\,\,p=15\,\,\,\,\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,p=\,-11\end{array}\)
Check the solutions in the original equation.
\(\displaystyle \begin{array}{r}\,\,\,\,\,\left| 2p-4 \right|=26\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 2p-4 \right|=26\\\left| 2(15)-4 \right|=26\,\,\,\,\,\,\,\left| 2(-11)-4 \right|=26\\\,\,\,\,\,\left| 30-4 \right|=26\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -22-4 \right|=26\\\,\,\,\,\,\,\,\,\,\,\,\,\left| 26 \right|=26\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -26 \right|=26\end{array}\)
Both solutions check!
Answer
\(p=-11\)[/hidden-answer]
In the next video, we show more examples of solving a simple absolute value equation.
Now let’s look at an example where you need to do an algebraic step or two before you can write your two equations. The goal here is to get the absolute value on one side of the equation by itself. Then we can proceed as we did in the previous example.
Example
Solve for w. \(3\left|4w–1\right|–5=10\)
[reveal-answer q=”303228″]Show Solution[/reveal-answer]
[hidden-answer a=”303228″]
Isolate the term with the absolute value by adding 5 to both sides.
\(\begin{array}{r}3\left|4w-1\right|-5=10\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,+5\,\,\,+5}\\ 3\left|4w-1\right|=15\end{array}\)
Divide both sides by 3. Now the absolute value is isolated.
\(\begin{array}{r} \underline{3\left|4w-1\right|}=\underline{15}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\,\\\left|4w-1\right|=\,\,5\end{array}\)
Write the two equations that will give an absolute value of 5 and solve them.
\(\displaystyle \begin{array}{r}4w-1=5\,\,\,\,\,\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,\,\,\,4w-1=-5\\\underline{\,\,\,\,\,\,\,+1\,\,+1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,\,\,+1\,\,\,\,\,+1}\\\,\,\,\,\,\underline{4w}=\underline{6}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{4w}\,\,\,\,\,\,\,=\underline{-4}\\4\,\,\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4\,\,\\\,\,\,\,\,\,\,\,w=\frac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,w=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,w=\frac{3}{2}\,\,\,\,\,\text{or}\,\,\,\,\,-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Check the solutions in the original equation.
\(\displaystyle \begin{array}{r}\,\,\,\,\,3\left| 4w-1\, \right|-5=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\left| 4w-1\, \right|-5=10\\\\3\left| 4\left( \frac{3}{2} \right)-1\, \right|-5=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\left| 4w-1\, \right|-5=10\\\\\,\,\,\,\,\,3\left| \frac{12}{2}-1\, \right|-5=10\,\,\,\,\,\,\,3\left| 4(-1)-1\, \right|-5=10\\\\\,\,\,\,\,\,\,\,3\left| 6-1\, \right|-5=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\left| -4-1\, \right|-5=10\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\left(5\right)-5=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\left| -5 \right|-5=10\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15-5=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15-5=10\\10=10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,10=10\end{array}\)
Both solutions check
Answer
\(w=-1\,\,\,\,\text{or}\,\,\,\,w=\frac{3}{2}\)[/hidden-answer]
In the two videos that follow, we show examples of how to solve an absolute value equation that requires you to isolate the absolute value first using mathematical operations.
The Distributive Property
As we solve linear equations, we often need to do some work to write the linear equations in a form we are familiar with solving. This section will focus on manipulating an equation we are asked to solve in such a way that we can use the skills we learned for solving multi-step equations to ultimately arrive at the solution.
Parentheses can make solving a problem difficult, if not impossible. To get rid of these unwanted parentheses we have the distributive property. Using this property we multiply the number in front of the parentheses by each term inside of the parentheses.
The Distributive Property of Multiplication
For all real numbers a, b, and c, \(a(b+c)=ab+ac\).
What this means is that when a number multiplies an expression inside parentheses, you can distribute the multiplication to each term of the expression individually. Then, you can follow the steps we have already practiced to isolate the variable and solve the equation.
Example
Solve for \(4\left(2a+3\right)=28\)
[reveal-answer q=”372387″]Show Solution[/reveal-answer]
[hidden-answer a=”372387″]
Apply the distributive property to expand \(8a+12\)
\(\begin{array}{r}4\left(2a+3\right)=28\\ 8a+12=28\end{array}\)
Subtract 12 from both sides to isolate the variable term.
\(\begin{array}{r}8a+12\,\,\,=\,\,\,28\\ \underline{-12\,\,\,\,\,\,-12}\\ 8a\,\,\,=\,\,\,16\end{array}\)
Divide both terms by 8 to get a coefficient of 1.
\(\begin{array}{r}\underline{8a}=\underline{16}\\8\,\,\,\,\,\,\,\,\,\,\,\,8\\a\,=\,\,2\end{array}\)
Answer
\(a=2\)[/hidden-answer]
In the video that follows, we show another example of how to use the distributive property to solve a multi-step linear equation.
In the next example, you will see that there are parentheses on both sides of the equal sign, so you will need to use the distributive property twice. Notice that you are going to need to distribute a negative number, so be careful with negative signs!
Example
Solve for \(2\left(4t-5\right)=-3\left(2t+1\right)\)
[reveal-answer q=”302387″]Show Solution[/reveal-answer]
[hidden-answer a=”302387″]
Apply the distributive property to expand \(8t-10\) and \(-6t-3\). Be careful in this step—you are distributing a negative number, so keep track of the sign of each number after you multiply.
\(\begin{array}{r}2\left(4t-5\right)=-3\left(2t+1\right)\,\,\,\,\,\, \\ 8t-10=-6t-3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Add \(-6t\) to both sides to begin combining like terms.
\(\begin{array}{r}8t-10=-6t-3\\ \underline{+6t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+6t}\,\,\,\,\,\,\,\\ 14t-10=\,\,\,\,-3\,\,\,\,\,\,\,\end{array}\)
Add 10 to both sides of the equation to isolate t.
\(\begin{array}{r}14t-10=-3\\ \underline{+10\,\,\,+10}\\ 14t=\,\,\,7\,\end{array}\)
The last step is to divide both sides by 14 to completely isolate t.
\(\begin{array}{r}14t=7\,\,\,\,\\\frac{14t}{14}=\frac{7}{14}\end{array}\)
Answer
\(t=\frac{1}{2}\)
We simplified the fraction \(\frac{1}{2}\)[/hidden-answer]
In the following video, we solve another multi-step equation with two sets of parentheses.
Sometimes, you will encounter a multi-step equation with fractions. If you prefer not working with fractions, you can use the multiplication property of equality to multiply both sides of the equation by a common denominator of all of the fractions in the equation. This will clear all the fractions out of the equation. See the example below.
Example
Solve \(\frac{1}{2}x-3=2-\frac{3}{4}x\) by clearing the fractions in the equation first.
[reveal-answer q=”129951″]Show Solution[/reveal-answer]
[hidden-answer a=”129951″]
Multiply both sides of the equation by 4, the common denominator of the fractional coefficients.
\(\begin{array}{r}\frac{1}{2}x-3=2-\frac{3}{4}x\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\end{array}\)
Use the distributive property to expand the expressions on both sides. Multiply.
\(\begin{array}{r}4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)-4\left(-\frac{3}{4}x\right)\\\\ \frac{4}{2}x-12=8-\frac{12}{4}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\\\ 2x-12=8-3x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array}\)
Add 3x to both sides to move the variable terms to only one side. Add 12 to both sides to move the variable terms to only one side.
\(\begin{array}{r}2x-12=8-3x\, \\\underline{+3x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+3x}\\ 5x-12=8\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Add 12 to both sides to move the constant terms to the other side.
\(\begin{array}{r}5x-12=8\,\,\\ \underline{\,\,\,\,\,\,+12\,+12} \\5x=20\end{array}\)
Divide to isolate the variable.
\(\begin{array}{r}\underline{5x}=\underline{5}\\ 5\,\,\,\,\,\,\,\,\,5\\ x=4\end{array}\)
Answer
\(x=4\)[/hidden-answer]
Of course, if you like to work with fractions, you can just apply your knowledge of operations with fractions and solve.
In the following video, we show how to solve a multi-step equation with fractions.
Regardless of which method you use to solve equations containing variables, you will get the same answer. You can choose the method you find the easiest! Remember to check your answer by substituting your solution into the original equation.
Sometimes, you will encounter a multi-step equation with decimals. If you prefer not working with decimals, you can use the multiplication property of equality to multiply both sides of the equation by a a factor of 10 that will help clear the decimals. See the example below.
Example
Solve \(3y+10.5=6.5+2.5y\) by clearing the decimals in the equation first.
[reveal-answer q=”159951″]Show Solution[/reveal-answer]
[hidden-answer a=”159951″]
Since the smallest decimal place represented in the equation is 0.10, we want to multiply by 10 to make 1.0 and clear the decimals from the equation.
\(\begin{array}{r}3y+10.5=6.5+2.5y\,\,\,\,\,\,\,\,\,\,\,\,\\\\ 10\left(3y+10.5\right)=10\left(6.5+2.5y\right)\end{array}\)
Use the distributive property to expand the expressions on both sides.
\(\begin{array}{r}10\left(3y\right)+10\left(10.5\right)=10\left(6.5\right)+10\left(2.5y\right)\end{array}\)
Multiply.
\(30y+105=65+25y\)
Move the smaller variable term, \(25y\), by subtracting it from both sides.
\(\begin{array}{r}30y+105=65+25y\,\,\\ \underline{-25y\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-25y} \\5y+105=65\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Subtract 105 from both sides to isolate the term with the variable.
\(\begin{array}{r}5y+105=65\,\,\,\\ \underline{\,\,\,\,\,\,-105\,-105} \\5y=-40\end{array}\)
Divide both sides by 5 to isolate the y.
\(\begin{array}{l}\underline{5y}=\underline{-40}\\ 5\,\,\,\,\,\,\,\,\,\,\,\,\,5\\ \,\,\,x=-8\end{array}\)
Answer
\(x=-8\)[/hidden-answer]
In the following video, we show another example of clearing decimals first to solve a multi-step linear equation.
Here are some steps to follow when you solve multi-step equations.
Solving Multi-Step Equations
1. (Optional) Multiply to clear any fractions or decimals.
2. Simplify each side by clearing parentheses and combining like terms.
3. Add or subtract to isolate the variable term—you may have to move a term with the variable.
4. Multiply or divide to isolate the variable.
5. Check the solution.
Classify Solutions to Linear Equations
There are three cases that can come up as we are solving linear equations. We have already seen one, where an equation has one solution. Sometimes we come across equations that don’t have any solutions, and even some that have an infinite number of solutions. The case where an equation has no solution is illustrated in the next examples.
Equations with no solutions
Example
Solve for x. \(12+2x–8=7x+5–5x\)
[reveal-answer q=”790409″]Show Solution[/reveal-answer]
[hidden-answer a=”790409″]
Combine like terms on both sides of the equation.
\(\displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{array}\)
Isolate the x term by subtracting 2x from both sides.
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end{array}\)
This false statement implies there are no solutions to this equation. Sometimes, we say the solution does not exist, or DNE for short.
[/hidden-answer]
This is not a solution! You did not find a value for x. Solving for x the way you know how, you arrive at the false statement \(4=5\). Surely 4 cannot be equal to 5!
This may make sense when you consider the second line in the solution where like terms were combined. If you multiply a number by 2 and add 4 you would never get the same answer as when you multiply that same number by 2 and add 5. Since there is no value of x that will ever make this a true statement, the solution to the equation above is “no solution.”
Be careful that you do not confuse the solution \(x=0\) means that the value 0 satisfies the equation, so there is a solution. “No solution” means that there is no value, not even 0, which would satisfy the equation.
Also, be careful not to make the mistake of thinking that the equation \(12+2x–8=7x+5–5x\) true.
Think About It
Try solving these equations. How many steps do you need to take before you can tell whether the equation has no solution or one solution?
a) Solve \(8y=3(y+4)+y\)
Use the textbox below to record how many steps you think it will take before you can tell whether there is no solution or one solution.
[practice-area rows=”1″][/practice-area]
[reveal-answer q=”933839″]Show Solution[/reveal-answer]
[hidden-answer a=”933839″]
Solve \(8y=3(y+4)+y\)
First, distribute the 3 into the parentheses on the right-hand side.
\(8y=3(y+4)+y=8y=3y+12+y\)
Next, begin combining like terms.
\(8y=3y+12+y = 8y=4y+12\)
Now move the variable terms to one side. Moving the \(4y\) will help avoid a negative sign.
\(\begin{array}{l}\,\,\,\,8y=4y+12\\\underline{-4y\,\,-4y}\\\,\,\,\,4y=12\end{array}\)
Now, divide each side by \(4y\).
\(\begin{array}{c}\frac{4y}{4}=\frac{12}{4}\\y=3\end{array}\)
Because we were able to isolate y on one side and a number on the other side, we have one solution to this equation.
[/hidden-answer]
b) Solve \(2\left(3x-5\right)-4x=2x+7\)
Use the textbox below to record how many steps you think it will take before you can tell whether there is no solution or one solution.
[practice-area rows=”1″][/practice-area]
[reveal-answer q=”937839″]Show Solution[/reveal-answer]
[hidden-answer a=”937839″]
Solve \(2\left(3x-5\right)-4x=2x+7\).
First, distribute the 2 into the parentheses on the left-hand side.
\(\begin{array}{r}2\left(3x-5\right)-4x=2x+7\\6x-10-4x=2x+7\end{array}\)
Now begin simplifying. You can combine the x terms on the left-hand side.
\(\begin{array}{r}6x-10-4x=2x+7\\2x-10=2x+7\end{array}\)
Now, take a moment to ponder this equation. It says that \(2x+7\). Can some number times two minus 10 be equal to that same number times two plus seven?
Let’s pretend \(x=3\).
Is it true that \(2\left(3\right)+7=13\). NO! We don’t even really need to continue solving the equation, but we can just to be thorough.
Add \(10\) to both sides.
\(\begin{array}{r}2x-10=2x+7\,\,\\\,\,\underline{+10\,\,\,\,\,\,\,\,\,\,\,+10}\\2x=2x+17\end{array}\)
Now move \(2x\) from the right hand side to combine like terms.
\(\begin{array}{l}\,\,\,\,\,2x=2x+17\\\,\,\underline{-2x\,\,-2x}\\\,\,\,\,\,\,\,0=17\end{array}\)
We know that \(0\text{ and }17\) are not equal, so there is no number that x could be to make this equation true.
This false statement implies there are no solutions to this equation, or DNE (does not exist) for short.
[/hidden-answer]
Algebraic Equations with an Infinite Number of Solutions
You have seen that if an equation has no solution, you end up with a false statement instead of a value for x. It is possible to have an equation where any value for x will provide a solution to the equation. In the example below, notice how combining the terms \(-4x\) on the left leaves us with an equation with exactly the same terms on both sides of the equal sign.
Example
Solve for x. \(5x+3–4x=3+x\)
[reveal-answer q=”773733″]Show Solution[/reveal-answer]
[hidden-answer a=”773733″]Combine like terms on both sides of the equation.
\(\displaystyle \begin{array}{r}5x+3-4x=3+x\\x+3=3+x\end{array}\)
Isolate the x term by subtracting x from both sides.
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,x+3=3+x\\\,\,\,\,\,\,\,\,\underline{\,-x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-x\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\,=\,\,3\end{array}\)
This true statement implies there are an infinite number of solutions to this equation, or we can also write the solution as “All Real Numbers”
[/hidden-answer]
You arrive at the true statement “\(x=0\) into the original equation—you will get a true statement! Try \(x=-\frac{3}{4}\), and it also will check!
This equation happens to have an infinite number of solutions. Any value for x that you can think of will make this equation true. When you think about the context of the problem, this makes sense—the equation \(x+3=3+x\) means “some number plus 3 is equal to 3 plus that same number.” We know that this is always true—it’s the commutative property of addition!
In the following video, we show more examples of attempting to solve a linear equation with either no solution or many solutions.
Example
Solve for x. \(3\left(2x-5\right)=6x-15\)
[reveal-answer q=”973733″]Show Solution[/reveal-answer]
[hidden-answer a=”973733″]
Distribute the 3 through the parentheses on the left-hand side.
\(\begin{array}{r}3\left(2x-5\right)=6x-15\\6x-15=6x-15\end{array}\)
Wait! This looks just like the previous example. You have the same expression on both sides of an equal sign. No matter what number you choose for x, you will have a true statement. We can finish the algebra:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,6x-15=6x-15\\\,\,\,\,\,\,\,\,\underline{\,-6x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-6x\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-15\,\,=\,\,-15\end{array}\)
This true statement implies there are an infinite number of solutions to this equation.
[/hidden-answer]
In this video, we show more examples of solving linear equations with either no solutions or many solutions.
In the following video, we show more examples of solving linear equations with parentheses that have either no solution or many solutions.
Absolute value equations with no solutions
As we are solving absolute value equations it is important to be aware of special cases. An absolute value is defined as the distance from 0 on a number line, so it must be a positive number. When an absolute value expression is equal to a negative number, we say the equation has no solution, or DNE. Notice how this happens in the next two examples.
Example
Solve for x. \(7+\left|2x-5\right|=4\)
[reveal-answer q=”173733″]Show Solution[/reveal-answer]
[hidden-answer a=”173733″]Notice absolute value is not alone. Subtract \(7\) from each side to isolate the absolute value.
\(\begin{array}{r}7+\left|2x-5\right|=4\,\,\,\,\\\underline{\,-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-7\,}\\\left|2x-5\right|=-3\end{array}\)
Result of absolute value is negative! The result of an absolute value must always be positive, so we say there is no solution to this equation, or DNE.
[/hidden-answer]
Example
Solve for x. \(-\frac{1}{2}\left|x+3\right|=6\)
[reveal-answer q=”173738″]Show Solution[/reveal-answer]
[hidden-answer a=”173738″]Notice absolute value is not alone, multiply both sides by the reciprocal of \(-2\).
\(\begin{array}{r}-\frac{1}{2}\left|x+3\right|=6\,\,\,\,\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\,\left(-2\right)-\frac{1}{2}\left|x+3\right|=\left(-2\right)6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left|x+3\right|=-12\,\,\,\,\,\end{array}\)
Again, we have a result where an absolute value is negative!
There is no solution to this equation, or DNE.
[/hidden-answer]
In this last video, we show more examples of absolute value equations that have no solutions.
Summary
Equations are mathematical statements that combine two expressions of equal value. An algebraic equation can be solved by isolating the variable on one side of the equation using the properties of equality. To check the solution of an algebraic equation, substitute the value of the variable into the original equation.
Complex, multi-step equations often require multi-step solutions. Before you can begin to isolate a variable, you may need to simplify the equation first. This may mean using the distributive property to remove parentheses or multiplying both sides of an equation by a common denominator to get rid of fractions. Sometimes it requires both techniques. If your multi-step equation has an absolute value, you will need to solve two equations, sometimes isolating the absolute value expression first.
We have also seen that solutions to equations can fall into three categories:
- One solution
- No solution, DNE (does not exist)
- Many solutions, also called infinitely many solutions or All Real Numbers
And sometimes, we don’t need to do much algebra to see what the outcome will be.
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Graphic: Equation, term, expression. Provided by: Lumen Learning. License: CC BY: Attribution
- Solving One Step Equations Using Multiplication and Division (Basic). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/BN7iVWWl2y0. License: CC BY: Attribution
- Solving Absolute Value Equation Using Multiplication and Division. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/CTLnJ955xzc. License: CC BY: Attribution
- Solving Two Step Equations (Basic). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/fCyxSVQKeRw. License: CC BY: Attribution
- Solving an Equation that Requires Combining Like Terms. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/ez_sP2OTGjU. License: CC BY: Attribution
- Solve an Equation with Variable on Both Sides. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/f3ujWNPL0Bw. License: CC BY: Attribution
- Solving an Equation with One Set of Parentheses. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/aQOkD8L57V0. License: CC BY: Attribution
- Solving an Equation with Parentheses on Both Sides. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/StomYTb7Xb8. License: CC BY: Attribution
- Solving an Equation with Fractions (Clear Fractions). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/AvJTPeACTY0. License: CC BY: Attribution
- Solving an Equation with Decimals (Clear Decimals). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/wtwepTZZnlY. License: CC BY: Attribution
- Linear Equations with No Solutions or Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/iLkZ3o4wVxU. License: CC BY: Attribution
- Linear Equations with No Solutions of Infinite Solutions (Parentheses). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/EU_NEo1QBJ0. License: CC BY: Attribution
- Absolute Value Equations with No Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/T-z5cQ58I_g. License: CC BY: Attribution
- Solve One-Step Equations Using Addition and Subtraction (Whole Numbers). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/VsWrFKFerSY. License: CC BY: Attribution
- Solving One Step Equations Using Addition and Subtraction (Integers). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/D3T8eCT5U_w. License: CC BY: Attribution
- Solving One Step Equations Using Addition and Subtraction (Decimals). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/D8wKGlxf6bM. License: CC BY: Attribution
- Solving One Step Equations Using Addition and Subtraction (Fractions). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/O7SPM7Cs8Ds. License: CC BY: Attribution
- Ex 1: Solving Absolute Value Equations. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/U-7fF-W8_xE. License: CC BY: Attribution
- Unit 10: Solving Equations and Inequalities, First Edition Developmental Math: An Open Program . Provided by: Monterey Institute of Technology. Located at: nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Solving One Step Equations Using Multiplication (Fractions). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/AhBdGeUGgsI. License: CC BY: Attribution
- Ex 4: Solving Absolute Value Equations (Requires Isolating Abs. Value). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/-HrOMkIiSfU. License: CC BY: Attribution
- Ex 5: Solving Absolute Value Equations (Requires Isolating Abs. Value). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/2bEA7HoDfpk. License: CC BY: Attribution
- Beginning and Intermediate Algebra. Authored by: Tyler Wallace. Located at: http://wallace.ccfaculty.org/book/book.html. License: CC BY: Attribution