6.3: Solve Simple Polynomial Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Greatest Common Factor
- Review the concept of greatest common factor
- Factor a Polynomial
- Simple Polynomial Equations
- Factor the greatest common monomial out of a polynomial
- Solve a polynomial in factored form by setting it equal to zero

In the section on the zero product principle, we showed that using the techniques for solving equations that we learned for linear equations did not work to solve
t(5−t)=0
But because the equation was written as the product of two terms, we could use the zero product principle. What if we are given a polynomial equation that is not written as a product of two terms, such as this one 2y2+4y=0? We can use a technique called factoring, where we try to find factors that can be divided into each term of the polynomial so it can be rewritten as a product.
In this section we will explore how to find common factors from the terms of a polynomial, and rewrite it as a product. This technique will help us solve polynomial equations in the next section.
Greatest Common Factor
When we studied fractions, we learned that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, 4 is the GCF of 16 and 20 because it is the largest number that divides evenly into both 16 and 20.The GCF of polynomials works the same way: 4x is the GCF of 16x and 20x2.
A General Note: Greatest Common Factor
The greatest common factor (GCF) of a group of given polynomials is the largest polynomial that divides evenly into the polynomials.
Factors are the building blocks of multiplication. They are the numbers that you can multiply together to produce another number: 2 and 10 are factors of 20, as are 4 and 5 and 1 and 20. To factor a number is to rewrite it as a product. 20=4⋅5. In algebra, we use the word factor as both a noun – something being multiplied – and as a verb – rewriting a sum or difference as a product.
To factor a polynomial, you rewrite it as a product. Any integer can be written as the product of factors, and we can apply this technique to monomials or polynomials. Factoring is very helpful in simplifying and solving equations using polynomials.

A prime factor is similar to a prime number—it has only itself and 1 as factors. The process of breaking a number down into its prime factors is called prime factorization.
To get acquainted with the idea of factoring, let’s first find the greatest common factor (GCF) of two whole numbers. The GCF of two numbers is the greatest number that is a factor of both of the numbers. Take the numbers 50 and 30.
50=10⋅530=10⋅3
Their greatest common factor is 10, since 10 is the greatest factor that both numbers have in common.
To find the GCF of greater numbers, you can factor each number to find their prime factors, identify the prime factors they have in common, and then multiply those together.
Example
Find the greatest common factor of 210 and 168.
[reveal-answer q=”803757″]Show Solution[/reveal-answer]
[hidden-answer a=”803757″]
210=2⋅3⋅5⋅7168=2⋅2⋅2⋅3⋅7GCF=2⋅3⋅7
Answer
GCF=42
[/hidden-answer]
Because the GCF is the product of the prime factors that these numbers have in common, you know that it is a factor of both numbers. (If you want to test this, go ahead and divide both 210 and 168 by 42—they are both evenly divisible by this number!)
The video that follows show another example of finding the greatest common factor of two whole numbers.
Finding the greatest common factor in a set of monomials is not very different from finding the GCF of two whole numbers. The method remains the same: factor each monomial independently, look for common factors, and then multiply them to get the GCF.
Example
Find the greatest common factor of 10b2.
[reveal-answer q=”210634″]Show Solution[/reveal-answer]
[hidden-answer a=”210634″]
25b3=5⋅5⋅b⋅b⋅b10b2=5⋅2⋅b⋅bGCF=5⋅b⋅b
Answer
GCF=5b2
[/hidden-answer]
The monomials have the factors 5, b, and b in common, which means their greatest common factor is 5b2.
The video that follows gives another example of finding the greatest common factor of two monomials with only one variable.
Example
Find the greatest common factor of 45c2d2.
[reveal-answer q=”930504″]Show Solution[/reveal-answer]
[hidden-answer a=”930504″]
81c3d=3⋅3⋅3⋅3⋅c⋅c⋅c⋅d45c2d2=3⋅3⋅5⋅c⋅c⋅d⋅dGCF=3⋅3⋅c⋅c⋅d
Answer
GCF=9c2d
[/hidden-answer]
The video that follows shows another example of finding the greatest common factor of two monomials with more than one variable.
Factor a Polynomial

Before we solve polynomial equations, we will practice finding the greatest common factor of a polynomial. If you can find common factors for each term of a polynomial, then you can factor it, and solving will be easier.
To help you practice finding common factors, identify factors that the terms of the polynomial have in common in the table below.
| Polynomial | Terms | Common Factors |
|---|---|---|
| a2–2a | −2a | a is a factor of −2a |
| 4c3 and 4c3 and 4c |
To factor a polynomial, first identify the greatest common factor of the terms. You can then use the distributive property to rewrite the polynomial in a factored form. Recall that the distributive property of multiplication over addition states that a product of a number and a sum is the same as the sum of the products.
Distributive Property Forward and Backward
Forward: Product of a number and a sum: a is being distributed over b+c.”
Backward: Sum of the products: a⋅b+a⋅c=a(b+c). Here you can say that “a is being factored out.”
We first learned that we could distribute a factor over a sum or difference, now we are learning that we can “undo” the distributive property with factoring.
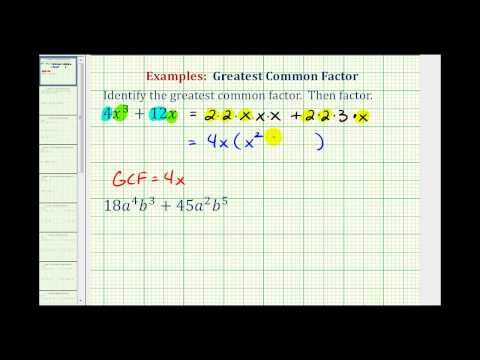
Example
Factor 25b3+10b2.
[reveal-answer q=”716902″]Show Solution[/reveal-answer]
[hidden-answer a=”716902″]Find the GCF. From a previous example, you found the GCF of 10b2 to be 5b2.
25b3=5⋅5⋅b⋅b⋅b10b2=5⋅2⋅b⋅bGCF=5⋅b⋅b=5b2
Rewrite each term with the GCF as one factor.
25b3=5b2⋅5b10b2=5b2⋅2
Rewrite the polynomial using the factored terms in place of the original terms.
5b2(5b)+5b2(2)
Factor out the 5b2.
5b2(5b+2)
Answer
5b2(5b+2)
[/hidden-answer]
The factored form of the polynomial 5b2(5b+2). You can check this by doing the multiplication. 5b2(5b+2)=25b3+10b2.
Note that if you do not factor the greatest common factor at first, you can continue factoring, rather than start all over.
For example:
25b3+10b2=5(5b3+2b2)Factor out 5.=5b2(5b+2)Factor out b2.
Notice that you arrive at the same simplified form whether you factor out the GCF immediately or if you pull out factors individually.
Example
Factor 81c3d+45c2d2.
[reveal-answer q=”809701″]Show Solution[/reveal-answer]
[hidden-answer a=”809701″]Factor 81c3d.
3⋅3⋅9⋅c⋅c⋅c⋅d
Factor 45c2d2.
3⋅3⋅5⋅c⋅c⋅d⋅d
Find the GCF.
3⋅3⋅c⋅c⋅d=9c2d
Rewrite each term as the product of the GCF and the remaining terms.
81c3d=9c2d(9c)45c2d2=9c2d(5d)
Rewrite the polynomial expression using the factored terms in place of the original terms.
9c2d(9c)+9c2d(5d)
Factor out 9c2d.
9c2d(9c+5d)
Answer
9c2d(9c+5d)
[/hidden-answer]
The following video provides two more examples of finding the greatest common factor of a binomial
Simple Polynomial Equations
In this section we will apply factoring a monomial from a polynomial to solving polynomial equations. Recall that not all of the techniques we use for solving linear equations will apply to solving polynomial equations, so we will be using the zero product principle to solve for a variable.
We will begin with an example where the polynomial is already equal to zero.
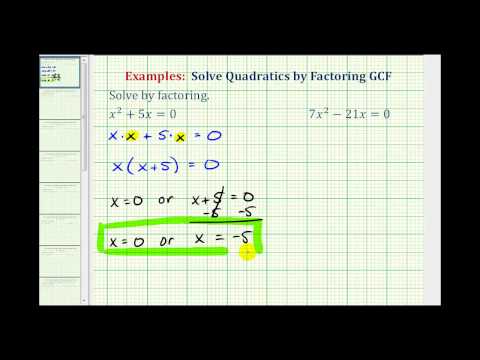
Example
Solve:
−t2+t=0
[reveal-answer q=”612316″]Show Solution[/reveal-answer]
[hidden-answer a=”612316″]
Each term has a common factor of t, so we can factor and use the zero product principle. Rewrite each term as the product of the GCF and the remaining terms.
−t2=t(−t)t=t(1)
Rewrite the polynomial equation using the factored terms in place of the original terms.
−t2+t=0t(−t)+t(1)t(−t+1)=0
Now we have a product on one side and zero on the other, so we can set each factor equal to zero using the zero product principle.
t=0 OR −t+1=0−1_−1_−t=−1−t−1=−1−1t=1
Answer
t=0 OR t=1
[/hidden-answer]
Notice how we were careful with signs in the last example. Even though one of the terms was negative, we factored out the positive common term of t. In the next example we will see what to do when the polynomial you are working with is not set equal to zero. Int eh followign video, we present more examples of solving quadratic equations by factoring.
Example
Solve: 6t=3t2−12t
[reveal-answer q=”162196″]Show Solution[/reveal-answer]
[hidden-answer a=”162196″]
First, move all the terms to one side. The goal is to try and see if we can use the zero product principle, since that is the only tool we know for solving polynomial equations.
6t=3t2−12t−6t_−6t_0=3t2−18t
We now have all the terms on the right side, and zero on the other side. Each term has a common factor of 3t, so we can factor and use the zero product principle. If you are uncertain how we found the common factor 3t, review the section on greatest common factor.
Rewrite each term as the product of the GCF and the remaining terms. Note how we leave the negative sign on the 6 when we factor 3t out of -18t.
3t2=3t(t)−18t=3t(−6)
Rewrite the polynomial equation using the factored terms in place of the original terms.
0=3t2−18t0=3t(t)+3t(−6)0=3t(t−6)
Solve the two equations.
0=t−6 OR 0=3t+6_+6_03=3t36=t OR 0=t
Answer
t=6 OR t=0
[/hidden-answer]
The video that follows provides another example of solving a polynomial equation using the zero product principle and factoring.
We will work through one more example that is similar to the ones above, except this example has fractions and the greatest common monomial is negative.
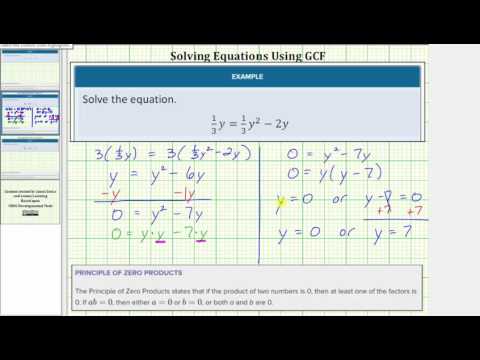
Example
Solve 12y=−4y−12y2
[reveal-answer q=”164090″]Show Solution[/reveal-answer]
[hidden-answer a=”164090″]We can solve this in one of two ways. One way is to eliminate the fractions like you may have done when solving linear equations, and the second is to find a common denominator and factor fractions. We will work through the second way.
First, we will find a common denominator, then factor fractions.
12y=−4y−12y20=−12y−4y−12y2
2 is a common denominator for −12y and −4y
22⋅−4y=−8y2
Rewrite the equation with the common denominator, then combine like terms.
0=−12y−4y−12y2 0=−12y−8y2−12y20=−92y−12y2
Find the greatest common factor of the terms of the polynomial:
Factors of −92y
−12⋅3⋅3⋅y
Factors of −12y2
−12⋅y⋅y
Both terms have −12 and y in common.
Rewrite each term as the product of the GCF and the remaining terms.
−92y=−12y(3⋅3)=−12y(9)
−12y2=−12y(y)
Rewrite the polynomial equation using the factored terms in place of the original terms. Pay attention to signs when we factor. Notice that we end up with a sum as a factor because the common factor is a negative number. (9+y)
0=−92y−12y2−12y(9)−12y(y)−12y(9+y)
Solve the two equations.
0=9+y OR 0=−12y−9_−9_−9=y OR 0=y
Answer
y=−9 OR y=0
[/hidden-answer]
Wow! In the last example, we used many skills to solve one equation. Let’s summarize them:
- We needed a common denominator to combine the like terms −4y and −12y, after we moved all the terms to one side of the equation
- We found the GCF of the terms −92y and −12y2
- We used the GCF to factor the polynomial −92y−12y2
- We used the zero product principle to solve the polynomial equation 0=−12y(9+y)
Sometimes solving an equation requires the combination of many algebraic principles and techniques. The last facet of solving the polynomial equation 12y=−4y−12y2 that we should talk about is negative signs.
We found that the GCF (9+y) as one of the factors of our final product.
In the following video we present another example of solving a quadratic polynomial with fractional coefficients using factoring and the zero product principle.
In the next unit, we will learn more factoring techniques that will allow you to be able to solve a wider variety of polynomial equations such as 3x2−x=2.
Summary
A whole number, monomial, or polynomial can be expressed as a product of factors. You can use some of the same logic that you apply to factoring integers to factoring polynomials. To factor a polynomial, first identify the greatest common factor of the terms, and then apply the distributive property to rewrite the expression. Once a polynomial in a(b+c), where a is the GCF, the polynomial is in factored form.
In this section we practiced using the zero product principle as a method for solving polynomial equations. We found that the techniques we used to solve linear equations did not give us the correct answer when used to solve a polynomial equation. We also found that a polynomial can be rewritten as a product by factoring out the greatest common factor. We used both factoring and the zero product principle to solve second degree polynomials.
- Screenshot One of These Things. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot Factor Tree. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot Prime Numbers. Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Factor and Solve a Quadratic Equation - GCF Only. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/oYytjgbd6Q0. License: CC BY: Attribution
- Factor and Solve a Quadratic Equation with Fractions - GCF Only . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/wm6DJ1bnaJs. License: CC BY: Attribution
- Example: Determining the Greatest Common Factor. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/KbBJcdDY_VE. License: CC BY: Attribution
- Ex: Determine the GCF of Two Monomials (One Variables). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/EhkVBXRBC2s. License: CC BY: Attribution
- Ex: Determine the GCF of Two Monomials (Two Variables). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/GfJvoIO3gKQ. License: CC BY: Attribution
- Ex 1: Identify GCF and Factor a Binomial. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/25_f_mVab_4. License: CC BY: Attribution
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Ex 1: Factor and Solve a Quadratic Equation - GCF . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/Hpb8DVYBDzA. License: CC BY: Attribution