6.4: More Factoring Methods
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Factor by Grouping
- Identify patterns that result from multiplying two binomials and how they affect factoring by grouping
- Factor a four term polynomial by grouping terms
- Methods for Factoring Trinomials
- Apply an algorithm to rewrite a trinomial as a four term polynomial
- Use factoring by grouping to factor a trinomial
- Use a shortcut to factor trinomials of the form ax2+bx+c
- Recognize where to place negative signs when factoring a trinomial
- Recognize when a polynomial is a difference of squares, and how it would factor as the product of two binomials
When we learned to multiply two binomials, we found that the result, before combining like terms, was a four term polynomial, as in this example: (x+4)(x+2)=x2+2x+4x+8.
We can apply what we have learned about factoring out a common monomial to return a four term polynomial to the product of two binomials. Why would we even want to do this?

Because it is an important step in learning techniques for factoring trinomials, such as the one you get when you simplify the product of the two binomials from above:
(x+4)(x+2)=x2+2x+4x+8=x2+6x+8
Additionally, factoring by grouping is a technique that allows us to factor a polynomial whose terms don’t all share a GCF. In the following example, we will introduce you to the technique. Remember, one of the main reasons to factor is because it will help solve polynomial equations.
Example
Factor a2+3a+5a+15
[reveal-answer q=”437455″]Show Solution[/reveal-answer]
[hidden-answer a=”437455″]
There isn’t a common factor between all four terms, so we will group the terms into pairs that will enable us to find a GCF for them. For example, we wouldn’t want to group a2 and 15 because they don’t share a common factor.
(a2+3a)+(5a+15)
Find the GCF of the first pair of terms.
a2=a⋅a3a=3⋅aGCF=a
Factor the GCF, a, out of the first group.
(a⋅a+a⋅3)+(5a+15)a(a+3)+(5a+15)
Find the GCF of the second pair of terms.
5a=5⋅a15=5⋅3GCF=5
Factor 5 out of the second group.
a(a+3)+(5⋅a+5⋅3)a(a+3)+5(a+3)
Notice that the two terms have a common factor (a+3).
a(a+3)+5(a+3)
Factor out the common factor (a+3) from the two terms.
(a+3)(a+5)
Note how the a and 5 become a binomial sum, and the other factor. This is probably the most confusing part of factoring by grouping.
Answer
a2+3a+5a+15=(a+3)(a+5)
[/hidden-answer]
Notice that when you factor a two term polynomial, the result is a monomial times a polynomial. But the factored form of a four-term polynomial is the product of two binomials. As we noted before, this is an important middle step in learning how to factor a three term polynomial.
This process is called the grouping technique. Broken down into individual steps, here’s how to do it (you can also follow this process in the example below).
- Group the terms of the polynomial into pairs that share a GCF.
- Find the greatest common factor and then use the distributive property to pull out the GCF
- Look for the common binomial between the factored terms
- Factor the common binomial out of the groups, the other factors will make the other binomial
Let’s try factoring a few more four-term polynomials. Note how there is a now a constant in front of the x2 term. We will just consider this another factor when we are finding the GCF.
Example
Factor 2x2+4x+5x+10.
[reveal-answer q=”313122″]Show Solution[/reveal-answer]
[hidden-answer a=”313122″]Group terms of the polynomial into pairs.
(2x2+4x)+(5x+10)
Factor out the like factor, 2x, from the first group.
2x(x+2)+(5x+10)
Factor out the like factor, 5, from the second group.
2x(x+2)+5(x+2)
Look for common factors between the factored forms of the paired terms. Here, the common factor is (x+2).
Factor out the common factor, (x+2), from both terms.
(2x+2)(x+5)
The polynomial is now factored.
Answer
(2x+2)(x+5)
[/hidden-answer]
Another example follows that contains subtraction. Note how we choose a positive GCF from each group of terms, and the negative signs stay.
Example
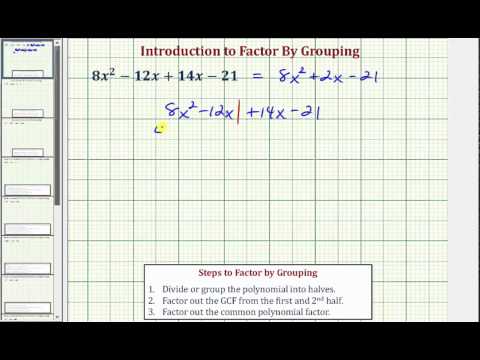
Factor 2x2–3x+8x–12.
[reveal-answer q=”715080″]Show Solution[/reveal-answer]
[hidden-answer a=”715080″]Group terms into pairs.
(2x2–3x)+(8x–12)
Factor the common factor, x, out of the first group and the common factor, 4, out of the second group.
x(2x–3)+4(2x–3)
Factor out the common factor, (2x–3), from both terms.
(x+4)(2x–3)
Answer
(x+4)(2x−3)
[/hidden-answer]
The video that follows provides another example of factoring by grouping.
In the next example, we will have a GCF that is negative. It is important to pay attention to what happens to the resulting binomial when the GCF is negative.
Example
Factor 3x2+3x–2x–2.
[reveal-answer q=”744005″]Show Solution[/reveal-answer]
[hidden-answer a=”744005″]Group terms into pairs.
(3x2+3x)+(−2x−2)
Factor the common factor 3x out of first group.
3x(x+1)+(−2x−2)
Factor the common factor −2 is factored out.
3x(x+1)−2(x+1)
Factor out the common factor, (x+1), from both terms.
(x+1)(3x−2)
Answer
(x+1)(3x−2)
[/hidden-answer]
In the following video we present another example of factoring by grouping when one of the GCF is negative.
Sometimes, you will encounter polynomials that, despite your best efforts, cannot be factored into the product of two binomials.
Example
Factor 7x2–21x+5x–5.
[reveal-answer q=”262926″]Show Solution[/reveal-answer]
[hidden-answer a=”262926″]Group terms into pairs.
(7x2–21x)+(5x–5)
Factor the common factor 7x out of the first group.
7x(x−3)+(5x−5)
Factor the common factor 5 out of the second group.
7x(x−3)+5(x−1)
The two groups 5(x–1) do not have any common factors, so this polynomial cannot be factored any further.
7x(x–3)+5(x–1)
Answer
Cannot be factored
[/hidden-answer]
In the example above, each pair can be factored, but then there is no common factor between the pairs!
Factor Trinomials Part I
In the last section we introduced the technique of factoring by grouping as a means to be able to factor a trinomial. Now we will actually get to the work of starting with a three term polynomial, and rewriting it as a four term polynomial so it can be factored.
We will start with factoring trinomials of the form x2 term.
Remember that when (x+5), are multiplied, the result is a four term polynomial and then it is simplified into a trinomial:
(x+2)(x+5)=x2+5x+2x+10=x2+7x+10
Factoring is the reverse of multiplying, so let’s go in reverse and factor the trinomial x2, 7x=5x+2x then we can use the grouping technique:
(x2+5x)+(2x+10)
Factor each pair: x(x+5)⏟+2(x+5)⏟common binomial factor
Then pull out the common binomial factor: (x+5)(x+2)
What would have happened if we had rewritten 6x+x?
(x2+6x)+(x+10)
Factor each pair: x(x+6)+1(x+10)
Then we don’t have a common factor of (x+5) like we did before. There is a method to the madness of choosing how to rewrite the middle terms so that you will end up with a common binomial factor.

The following is a summary of the method, then we will show some examples of how to use it.
Factoring Trinomials in the form x2+bx+c
To factor a trinomial in the form x2+bx+c, find two integers, r and s, whose product is c and whose sum is b.
r⋅s=c and r+s=b
Rewrite the trinomial as (x+r) and (x+s).
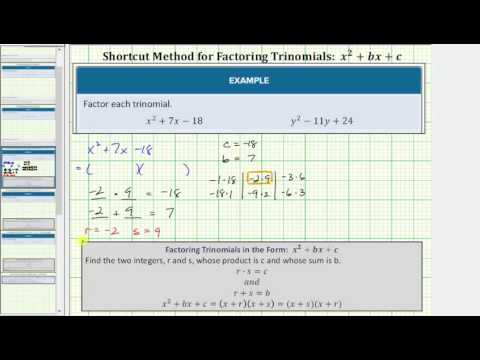
For example, to factor x2+7x+10, you are looking for two numbers whose sum is 7 (the coefficient of the middle term) and whose product is 10 (the last term).
Look at factor pairs of 10:1 and 10, 2, and 5. Do either of these pairs have a sum of 7? Yes, 2 and 5. So you can rewrite 2x+5x, and continue factoring as in the example above. Note that you can also rewrite 5x+2x. Both will work.
Let’s factor the trinomial x2+5x+6. In this polynomial, the b part of the middle term is 5 and the c term is 6. A chart will help us organize possibilities. On the left, list all possible factors of the c term, 6; on the right you’ll find the sums.
| Factors whose product is 6 | Sum of the factors |
|---|---|
| 1+6=7 | |
| 2+3=5 |
There are only two possible factor combinations, 1 and 6, and 2 and 3. You can see that 2x+3x=5x, giving us the correct middle term.
Example
Factor x2+5x+6.
[reveal-answer q=”141663″]Show Solution[/reveal-answer]
[hidden-answer a=”141663″]Use values from the chart above. Replace 2x+3x.
x2+2x+3x+6
Group the pairs of terms.
(x2+2x)+(3x+6)
Factor x out of the first pair of terms
x(x+2)+(3x+6)
Factor 3 out of the second pair of terms.
x(x+2)+3(x+2)
Factor out (x+2).
(x+2)(x+3)
Answer
(x+2)(x+3)
[/hidden-answer]
Note that if you wrote x2+3x+2x+6 and grouped the pairs as x(x+3)+2(x+3), and factored out (x+3)(x+2). Since multiplication is commutative, the order of the factors does not matter. So this answer is correct as well; they are equivalent answers.
In the following video, we present another example of how to use grouping to factor a quadratic polynomial.
Finally, let’s take a look at the trinomial −12. So look at all of the combinations of factors whose product is −12. Then see which of these combinations will give you the correct middle term, where b is 1.
| Factors whose product is 1⋅−12=−12 | 2⋅−6=−12 | 3⋅−4=−12 | 4⋅−3=−12 | 6⋅−2=−12 | 12⋅−1=−12 | 12+−1=11 |
|---|
There is only one combination where the product is r=4, and s=−3. Let’s use these to factor our original trinomial.
Example
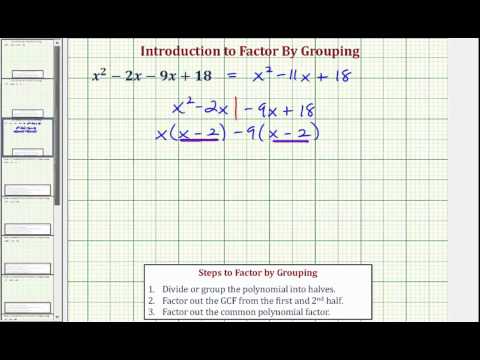
Factor x2+x–12.
[reveal-answer q=”205737″]Show Solution[/reveal-answer]
[hidden-answer a=”205737″]Rewrite the trinomial using the values from the chart above. Use values s=−3.
x2+4x+−3x–12
Group pairs of terms.
(x2+4x)+(−3x–12)
Factor x out of the first group.
x(x+4)+(−3x−12)
Factor −3 out of the second group.
x(x+4)–3(x+4)
Factor out (x+4).
(x+4)(x−3)
Answer
(x+4)(x−3)
[/hidden-answer]
In the above example, you could also rewrite x2–3x+4x–12 first. Then factor (x–3) getting (x–3)(x+4). Since multiplication is commutative, this is the same answer.
Factoring Tips
Factoring trinomials is a matter of practice and patience. Sometimes, the appropriate number combinations will just pop out and seem so obvious! Other times, despite trying many possibilities, the correct combinations are hard to find. And, there are times when the trinomial cannot be factored.
While there is no foolproof way to find the right combination on the first guess, there are some tips that can ease the way.
Tips for Finding Values that Work
When factoring a trinomial in the form x2+bx+c, consider the following tips.
Look at the c term first.
- If the c term is a positive number, then the factors of c will both be positive or both be negative. In other words, r and s will have the same sign.
- If the c term is a negative number, then one factor of c will be positive, and one factor of c will be negative. Either r or s will be negative, but not both.
Look at the b term second.
- If the c term is positive and the b term is positive, then both r and s are positive.
- If the c term is positive and the b term is negative, then both r and s are negative.
- If the c term is negative and the b term is positive, then the factor that is positive will have the greater absolute value. That is, if |r|>|s|, then r is positive and s is negative.
- If the c term is negative and the b term is negative, then the factor that is negative will have the greater absolute value. That is, if |r|>|s|, then r is negative and s is positive.
After you have factored a number of trinomials in the form x2+bx+c, you may notice that the numbers you identify for r and s end up being included in the factored form of the trinomial. Have a look at the following chart, which reviews the three problems you have seen so far.
| Trinomial | x2+5x+6 | r=+5,s=+2 | r=+4,s=–3 |
|---|---|---|---|
| Factored form | (x+2)(x+3) | (x+4)(x–3) |
The Shortcut
Notice that in each of the examples above, the r and s values are repeated in the factored form of the trinomial. So what does this mean? It means that in trinomials of the form x2 is 1), if you can identify the correct r and s values, you can effectively skip the grouping steps and go right to the factored form. For those of you that like shortcuts, let’s look at some examples where we use this idea.

In the next two examples, we will show how you can skip the step of factoring by grouping and move directly to the factored form of a product of two binomials with the r and s values that you find. The idea is that you can build factors for a trinomial in this form: x2+bx+c by finding r and s, then placing them in two binomial factors like this:
(x+r)(x+s) OR (x+s)(x+r)
Example
Factor: y2+6y−27
[reveal-answer q=”601131″]Show Solution[/reveal-answer]
[hidden-answer a=”601131″]
Find r and s:
| Factors whose product is -27 | Sum of the factors |
|---|---|
| 1−27=−26 | |
| 3−9=−6 | |
| −3+9=6 |
Instead of rewriting the middle term, we will use the values of r and s that give the product and sum that we need.
In this case:
r=−3s=9
It helps to start by writing two empty sets of parentheses:
()()
The squared term is y, so we will place a y in each set of parentheses:
(y)(y)
Now we can fill in the rest of each binomial with the values we found for r and s.
(y−3)(y+9)
Note how we kept the sign on each of the values. The nice thing about factoring is you can check your work. Multiply the binomials together to see if you did it correctly.
(y−3)(y+9)=y2+9y−3y−27=y2+6y−27
Answer
(y−3)(y+9)
[/hidden-answer]
We will show one more example so you can gain more experience.
Example
Factor: −m2+16m−48
[reveal-answer q=”402116″]Show Solution[/reveal-answer]
[hidden-answer a=”402116″]
There is a negative in front of the squared term, so we will factor out a negative one from the whole trinomial first. Remember, this boils down to changing the sign of all the terms:
−m2+16m−48=−1(m2−16m+48)
Now we can factor (m2−16m+48) by finding r and s. Note that b is negative, and c is positive so we are probably looking for two negative numbers:
| Factors whose product is 48 | Sum of the factors |
|---|---|
| −1−48=−49 | |
| −2−12=−14 | |
| −3−16=−19 | |
| −4−12=−16 |
There are more factors whose product is 48, but we have found the ones that sum to -16, so we can stop.
r=−4s=−12
Now we can fill in each binomial with the values we found for r and s, make sure to use the correct variable!
(m−4)(m−12)
We are not done yet, remember that we factored out a negative sign in the first step. We need to remember to include that.
−1(m−4)(m−12)
Answer
−m2+16m−48=−1(m−4)(m−12)
[/hidden-answer]
In the following video, we present two more examples of factoring a trinomial using the shortcut presented here.
Factor Trinomials Part II
The next goal is for you to be comfortable with recognizing where to place negative signs, and whether a trinomial can even be factored. Additionally, we will explore one special case to look out for at the end of this page.
Not all trinomials look like x2 term is 1. In these cases, your first step should be to look for common factors for the three terms.
| Trinomial | Factor out Common Factor | Factored |
|---|---|---|
| 2(x2+5x+6) | −5a2−15a−10 | −5(a+2)(a+1) |
| c(c2–8c+15) | y4–9y3–10y2 | y2(y–10)(y+1) |
Notice that once you have identified and pulled out the common factor, you can factor the remaining trinomial as usual. This process is shown below.
Example
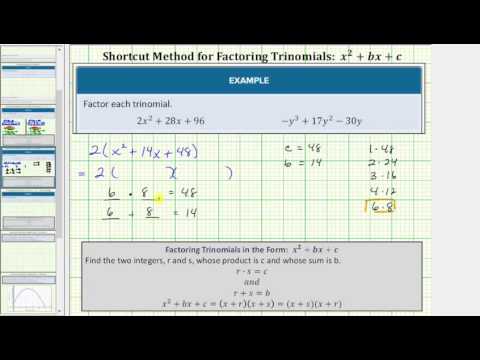
Factor 3x3–3x2–90x.
[reveal-answer q=”298928″]Show Solution[/reveal-answer]
[hidden-answer a=”298928″]Since 3 is a common factor for the three terms, factor out the 3.
3(x3–x2–30x)
x is also a common factor, so factor out x.
3x(x2–x–30)
Now you can factor the trinomial −30 and whose sum is −1.
The pair of factors is 5. So replace −6x+5x.
3x(x2–6x+5x–30)
Use grouping to consider the terms in pairs.
3x[(x2–6x)+(5x–30)]
Factor x out of the first group and factor 5 out of the second group.
3x[(x(x–6))+5(x–6)]
Then factor out x–6.
3x(x–6)(x+5)
Answer
3x(x–6)(x+5)
[/hidden-answer]
The following video contains two more examples of factoring a quadratic trinomial where the first step is to factor out a GCF. We use the shortcut method instead of factoring by grouping.
The general form of trinomials with a leading coefficient of a is x2 term, instead of an ax2 term.
However, if the coefficients of all three terms of a trinomial don’t have a common factor, then you will need to factor the trinomial with a coefficient of something other than 1.
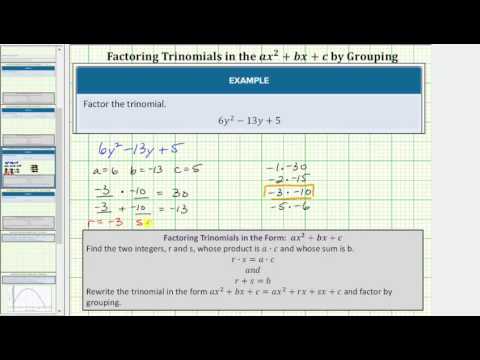
Factoring Trinomials in the form ax2+bx+c
To factor a trinomial in the form ax2+bx+c, find two integers, r and s, whose sum is b and whose product is ac.
r⋅s=a⋅cr+s=b
Rewrite the trinomial as ax2+rx+sx+c and then use grouping and the distributive property to factor the polynomial.
This is almost the same as factoring trinomials in the form a=1. Now you are looking for two factors whose product is a⋅c, and whose sum is b.
Let’s see how this strategy works by factoring 6z2+11z+4.
In this trinomial, b=11, and b=11 and whose product is a⋅c=6⋅4=24. You can make a chart to organize the possible factor combinations. (Notice that this chart only has positive numbers. Since ac is positive and b is positive, you can be certain that the two factors you’re looking for are also positive numbers.)
| Factors whose product is 24 | Sum of the factors |
|---|---|
| 1+24=25 | |
| 2+12=14 | |
| 3+8=11 | |
| 4+6=10 |
There is only one combination where the product is 24 and the sum is 11, and that is when s=8. Let’s use these values to factor the original trinomial.
Example
Factor 11z, as 3z+8z (from the chart above.)
6z2+3z+8z+4
Group pairs. Use grouping to consider the terms in pairs.
(6z2+3z)+(8z+4)
Factor 3z out of the first group and 4 out of the second group.
3z(2z+1)+4(2z+1)
Factor out (2z+1).
(2z+1)(3z+4)
Answer
(2z+1)(3z+4)
[/hidden-answer]
In the following video, we present another example of factoring a trinomial using grouping. In this example, the middle term, b, is negative. Note how having a negative middle term and a positive c term influence the options for r and s when factoring.
Before going any further, it is worth mentioning that not all trinomials can be factored using integer pairs. Take the trinomial b=35 and whose product is a⋅c=2⋅7=14? There are none! This type of trinomial, which cannot be factored using integers, is called a prime trinomial.
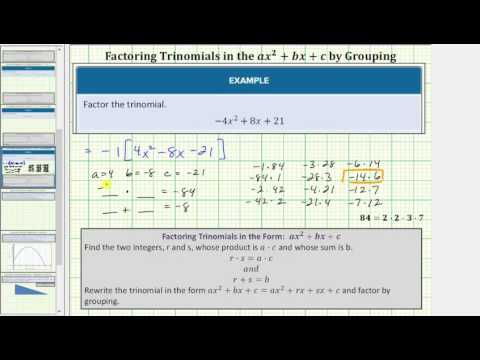
In some situations, a is negative, as in −1 as the first step in factoring, as doing so will change the sign of ax2 from negative to positive, making the remaining trinomial easier to factor.
Example
Factor −1 out of the trinomial. Notice that the signs of all three terms have changed.
−1(4h2–11h–3)
To factor the trinomial, you need to figure out how to rewrite rs=4⋅−3=−12, and the sum of rs=−11.
| r+s=−11 |
| −12+1=−11 |
| −6+2=−4 |
| −4+3=−1 |
Rewrite the middle term −12h+1h.
−1(4h2–12h+1h–3)
Group terms.
−1[(4h2–12h)+(1h–3)]
Factor out 4h from the first pair. The second group cannot be factored further, but you can write it as +1(h–3)=(h–3). This helps with factoring in the next step.
−1[4h(h–3)+1(h–3)]
Factor out a common factor of (h–3)(4h+1); the +1(h–3) in the previous step.
−1[(h–3)(4h+1)]
Answer
−1(h–3)(4h+1)
[/hidden-answer]
Note that the answer above can also be written as (h–3)(−4h–1) if you multiply −1 times one of the other factors.
In the following video we present another example of factoring a trinomial in the form −ax2+bx+c using the grouping technique.
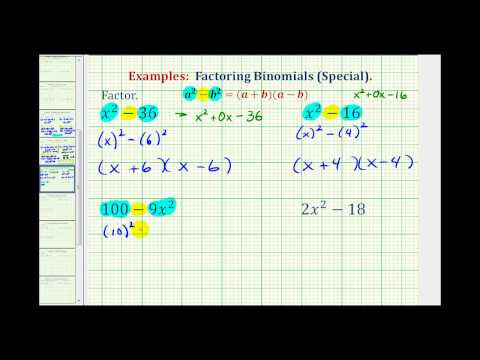
Difference of Squares
We would be remiss if we failed to introduce one more type of polynomial that can be factored. This polynomial can be factored into two binomials but has only two terms. Let’s start from the product of two binomials to see the pattern.
Given the product of two binomials: (x−2)(x+2), if we multiply them together, we lose the middle term that we are used to seeing as a result.
Multiply:
(x−2)(x+2)=x2−2x+2x−22=x2−22=x2−4
The polynomial x2−4 is called a difference of squares because teach term can be written as something squared. A difference of squares will always factor in the following way:
Factor a Difference of Squares
Given (a+b)(a−b)
Let’s factor x2+0x–4. This is similar in format to the trinomials we have been factoring so far, so let’s use the same method.
Find the factors of a⋅c whose sum is b, in this case, 0:
| Factors of 1⋅−4=−4 | 2⋅−2=−4 | −1⋅4=−4 | −1+4=3 |
|---|
2, and -2 have a sum of 0. You can use these to factor x2–4.
Example
Factor 0x as −2x+2x.
x2+0x−4x2−2x+2x−4
Group pairs.
(x2–2x)+(2x–4)
Factor x out of the first group. Factor 2 out of the second group.
x(x–2)+2(x–2)
Factor out (x–2).
(x–2)(x+2)
Answer
(3x–2)(3x+2)
[/hidden-answer]
Since order doesn’t matter with multiplication, the answer can also be written as \left(x+2\right)\left(x–2\right).
You can check the answer by multiplying \left(x–2\right)\left(x+2\right)=x^{2}+2x–2x–4=x^{2}–4.
The following video show two more examples of factoring a difference of squares.
Summary
When a trinomial is in the form of ax^{2}+bx+c, find two integers, r and s, whose sum is b and whose product is ac. Then rewrite the trinomial as ax^{2}+rx+sx+c and use grouping and the distributive property to factor the polynomial.
When −1 out of the whole trinomial before continuing.
A difference of squares \left(a+b\right)\left(a-b\right).
Summary
Trinomials in the form x^{2}+rx+sx+c and then use grouping and the distributive property to factor the polynomial.
- Screenshot: Why Should I Care?. Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: Method to the Madness. Provided by: Lumen Learning. License: CC BY: Attribution
- Image: Shortcut This Way. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 2: Intro to Factor By Grouping Technique. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/RR5nj7RFSiU. License: CC BY: Attribution
- Ex 1: Intro to Factor By Grouping Technique Mathispower4u . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/0dvGmDGVC5U. License: CC BY: Attribution
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Ex 1: Factor a Quadratic Expression Using Grouping When a = 1 . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/_Rtp7nSxf6c. License: CC BY: Attribution
- Factor a Trinomial Using the Shortcut Method - Form x^2+bx+c. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/-SVBVVYVNTM. License: CC BY: Attribution
- Ex: Factor a Difference of Squares. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/Li9IBp5HrFA. License: CC BY: Attribution