7.3: Operations on Rational Expressions

Learning Objectives

• Multiply and divide rational expressions
• Add and subtract rational expressions
  • Add and subtract rational expressions with like denominators
  • Add and subtract rational expressions with unlike denominators using a greatest common denominator
  • Add and subtract rational expressions that share no common factors
  • Add and subtract more than two rational expressions

Just as you can multiply and divide fractions, you can multiply and divide rational expressions. In fact, you use the same processes for multiplying and dividing rational expressions as you use for multiplying and dividing numeric fractions. The process is the same even though the expressions look different!

Multiply and Divide

Multiply Rational Expressions

Remember that there are two ways to multiply numeric fractions.

One way is to multiply the numerators and the denominators and then simplify the product, as shown here.

\(\displaystyle \frac{4}{5}\cdot \frac{9}{8}=\frac{36}{40}=\frac{3\cdot 3\cdot 2\cdot 2}{5\cdot 2\cdot 2\cdot 2}=\frac{3\cdot 3\cdot \cancel{2}\cdot\cancel{2}}{5\cdot \cancel{2}\cdot\cancel{2}\cdot 2}=\frac{3\cdot 3}{5\cdot 2}\cdot 1=\frac{9}{10}\)

A second way is to factor and simplify the fractions before performing the multiplication.

\(\frac{4}{5}\cdot\frac{9}{8}=\frac{2\cdot2}{5}\cdot\frac{3\cdot3}{2\cdot2\cdot2}=\frac{\cancel{2}\cdot\cancel{2}\cdot3\cdot3}{\cancel{2}\cdot5\cdot\cancel{2}\cdot2}=1\cdot\frac{3\cdot3}{5\cdot2}=\frac{9}{10}\)

Notice that both methods result in the same product. In some cases you may find it easier to multiply and then simplify, while in others it may make more sense to simplify fractions before multiplying.

The same two approaches can be applied to rational expressions. In the following examples, both techniques are shown. First, let’s multiply and then simplify.

Example

Multiply.\(\displaystyle \frac{5

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/p[1]/span[1], line 1, column 2

}{14}\cdot \frac{7}{10

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/p[1]/span[2], line 1, column 2

}\)

State the product in simplest form.

[reveal-answer q=”518862″]Show Solution[/reveal-answer]
[hidden-answer a=”518862″]

Multiply the numerators, and then multiply the denominators.

\(\frac{5a^{2}}{14}\cdot\frac{7}{10a^{3}}=\frac{35a^{2}}{140a^{3}}\)

Simplify by finding common factors in the numerator and denominator. Simplify the common factors.

\(\large\begin{array}{l}\frac{35a^{2}}{140a^{3}}=\frac{5\cdot7\cdot{a}^{2}}{5\cdot7\cdot2\cdot2\cdot{a}^{2}\cdot{a}}\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{\cancel{5}\cdot\cancel{7}\cdot\cancel

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/p[7]/span[1], line 1, column 2

}{\cancel{5}\cdot\cancel{7}\cdot2\cdot2\cdot\cancel

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/p[7]/span[2], line 1, column 2

\cdot{a}}\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\normalsize1\cdot\large\frac{1}{4a}\end{array}\)

Simplify.

\(\displaystyle \frac{1}{4a}\)

Answer

\(\displaystyle \frac{5

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/div/p[1]/span[1], line 1, column 2

}{14}\cdot \frac{7}{10

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[4]/div/p[1]/span[2], line 1, column 2

}=\frac{1}{4a}\) \(\displaystyle\)

[/hidden-answer]

Okay, that worked. But this time let’s simplify first, then multiply. When using this method, it helps to look for the greatest common factor. You can factor out any common factors, but finding the greatest one will take fewer steps.

Example

Multiply. \(\frac{5a^{2}}{14}\cdot\frac{7}{10a^{3}}\)

State the product in simplest form.

[reveal-answer q=”724339″]Show Solution[/reveal-answer]
[hidden-answer a=”724339″]

Factor the numerators and denominators. Look for the greatest common factors.

\(\displaystyle \frac{5\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[5]/span[1], line 1, column 2

}{7\cdot 2}\cdot \frac{7}{5\cdot 2\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[5]/span[2], line 1, column 2

\cdot a}\)

Simplify common factors, then multiply.

\(\large\begin{array}{c}\frac{5\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[7]/span[1], line 1, column 2

}{7\cdot 2}\cdot \frac{7}{5\cdot 2\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[7]/span[2], line 1, column 2

\cdot a}\\\\=\frac{\cancel{5}\cdot\cancel

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[7]/span[3], line 1, column 2

}{\cancel{7}\cdot 2}\cdot \frac{\cancel{7}}{\cancel{5}\cdot 2\cdot\cancel

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[5]/p[7]/span[4], line 1, column 2

\cdot a}\\\\=\frac{1\cdot1\cdot1}{2\cdot2\cdot{a}}=\frac{1}{4a}\end{array}\)

Answer

\(\frac{5a^{2}}{14}\cdot\frac{7}{10a^{3}}=\frac{1}{4a}\)

[/hidden-answer]

Both methods produced the same answer.

Also, remember that when working with rational expressions, you should get into the habit of identifying any values for the variables that would result in division by 0. These excluded values must be eliminated from the domain, the set of all possible values of the variable. In the example above, \(a=0\), the denominator of the fraction \(\frac{7}{10a^{3}}\) equals 0, which will make the fraction undefined.

Some rational expressions contain quadratic expressions and other multi-term polynomials. To multiply these rational expressions, the best approach is to first factor the polynomials and then look for common factors. (Multiplying the terms before factoring will often create complicated polynomials…and then you will have to factor these polynomials anyway! For this reason, it is easier to factor, simplify, and then multiply.) Just take it step by step, like in the examples below.

Example

Multiply. \(\displaystyle \frac{{{a}^{2}}-a-2}{5a}\cdot \frac{10a}{a+1}\,\,,\,\,\,\,\,\,a\,\ne \,\,-1\,,\,\,0\)

State the product in simplest form.

[reveal-answer q=”794041″]Show Solution[/reveal-answer]
[hidden-answer a=”794041″]

Factor the numerators and denominators.

\(\frac{\left(a-2\right)\left(a+1\right)}{5\cdot{a}}\cdot\frac{5\cdot2\cdot{a}}{\left(a+1\right)}\)

Simplify common factors:

\(\large\begin{array}{c}\frac{\left(a-2\right)\cancel{\left(a+1\right)}}{\cancel{5}\cdot{\cancel{a}}}\cdot\frac{\cancel{5}\cdot2\cdot{\cancel{a}}}{\cancel{\left(a+1\right)}}\\\\=\frac{a-2}{1}\cdot\frac{2}{1}\end{array}\)

Multiply simplified rational expressions. This expression can be left with the numerator in factored form or multiplied out.

\(\begin{array}{c}\frac{\left(a-2\right)}{1}\cdot\frac{2}{1}\\\\=2\left(a-2\right)\end{array}\)

Answer

\(\displaystyle \frac{{{a}^{2}}-a-2}{5a}\cdot \frac{10a}{a+1}=2a-4\)

[/hidden-answer]

Example

Multiply. \(\frac{a^{2}+4a+4}{2a^{2}-a-10}\cdot\frac{a+5}{a^{2}+2a},\,\,\,a\neq-2,0,\frac{5}{2}\)

State the product in simplest form.

[reveal-answer q=”980309″]Show Solution[/reveal-answer]
[hidden-answer a=”980309″]

Factor the numerators and denominators.

\(\frac{\left(a+2\right)\left(a+2\right)}{\left(2a-5\right)\left(a+2\right)}\cdot\frac{a+5}{a\left(a+2\right)}\)

Simplify common factors.

\(\large\frac{\cancel{\left(a+2\right)}\cancel{\left(a+2\right)}}{\left(2a-5\right)\cancel{\left(a+2\right)}}\cdot\frac{a+5}{a\cancel{\left(a+2\right)}}\)

Multiply simplified rational expressions. This expression can be left with the denominator in factored form or multiplied out.

\(\frac{1}{\left(2a-5\right)}\cdot\frac{a+5}{a}=\frac{a+5}{a\left(2a-5\right)}\)

Answer

\(\frac{a^{2}+4a+4}{2a^{2}-a-10}\cdot\frac{a+5}{a^{2}+2a}=\frac{a+5}{a\left(2a-5\right)}\)

[/hidden-answer]

Note that in the answer above, you cannot simplify the rational expression any further. It may be tempting to express the 5’s in the numerator and denominator as the fraction \(\frac{5}{5}\), but these 5’s are terms because they are being added or subtracted. Remember that only common factors, not terms, can be regrouped to form factors of 1!

In the following video we present another example of multiplying rational expressions.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Divide Rational Expressions

You’ve seen that you multiply rational expressions as you multiply numeric fractions. It should come as no surprise that you also divide rational expressions the same way you divide numeric fractions. Specifically, to divide rational expressions, keep the first rational expression, change the division sign to multiplication, and then take the reciprocal of the second rational expression.

Let’s begin by recalling division of numerical fractions.

\(\frac{2}{3}\div\frac{5}{9}=\frac{2}{3}\cdot\frac{9}{5}=\frac{18}{15}=\frac{6}{5}\)

Use the same process to divide rational expressions. You can think of division as multiplication by the reciprocal, and then use what you know about multiplication to simplify.

Reciprocal Architecture

You do still need to think about the domain, specifically the variable values that would make either denominator equal zero. But there’s a new consideration this time—because you divide by multiplying by the reciprocal of one of the rational expressions, you also need to find the values that would make the numerator of that expression equal zero. Have a look.

Example

Identify the domain of the expression. \(\frac{5x^{2}}{9}\div\frac{15x^{3}}{27}\)

[reveal-answer q=”988831″]Show Solution[/reveal-answer]
[hidden-answer a=”988831″]

Find excluded values. 9 and 27 can never equal 0.

Because \(\displaystyle \frac{15

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[2]/p[4]/span, line 1, column 2

}{27}\), you must find the values of x that would make \(15x^{3}\) equal 0.

\(\begin{array}{c}15x^{3}=0\\x=0\,\text{is an excluded value}.\end{array}\)

Answer

The domain is all real numbers except 0.

[/hidden-answer]

Knowing how to find the domain may seem unimportant here, but it will help you when you learn how to solve rational equations. To divide, multiply by the reciprocal.

Example

Divide. \(\frac{5x^{2}}{9}\div\frac{15x^{3}}{27}\)

State the quotient in simplest form.

[reveal-answer q=”688236″]Show Solution[/reveal-answer]
[hidden-answer a=”688236″]

Rewrite division as multiplication by the reciprocal.

\(\frac{5x^{2}}{9}\cdot\frac{27}{15x^{3}}\)

Factor the numerators and denominators.

\(\frac{5\cdot{x}\cdot{x}}{3\cdot3}\cdot\frac{3\cdot3\cdot3}{5\cdot3\cdot{x}\cdot{x}\cdot{x}}\)

Simplify common factors.

Simplify.

\(\large\begin{array}{c}\frac{\cancel{5}\cdot{\cancel{x}}\cdot{\cancel{x}}}{\cancel{3}\cdot\cancel{3}}\cdot\frac{\cancel{3}\cdot\cancel{3}\cdot\cancel{3}}{\cancel{5}\cdot\cancel{3}\cdot{\cancel{x}}\cdot{\cancel{x}}\cdot{x}}\\\\=\frac{1}{x}\end{array}\)

Answer

\(\displaystyle \frac{5

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[3]/div/p[1]/span[1], line 1, column 2

}{9}\div \frac{15

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[3]/div/p[1]/span[2], line 1, column 2

}{27}=\frac{1}{x},x\ne 0\)

[/hidden-answer]

Example

Divide. \(\frac{3x^{2}}{x+2}\div\frac{6x^{4}}{\left(x^{2}+5x+6\right)}\)

State the quotient in simplest form, and express the domain of the expression.

[reveal-answer q=”53255″]Show Solution[/reveal-answer]
[hidden-answer a=”53255″]

Determine the excluded values that make the denominators and the numerator of the divisor equal to 0.

\(\begin{array}{r}\left(x+2\right)=0\,\,\,\,\,\\x=-2\\\left(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/p[5]/span, line 1, column 2

+5x+6 \right)=0\,\,\,\,\,\\\left(x+3\right)\left(x+2\right)=0\,\,\,\,\,\\x=-3\,\,\,\,\text{or}\,\,\,\,-2\\6x^{4}=0\,\,\,\,\,\\x=0\,\,\,\,\,\end{array}\)

Domain is all real numbers except \(−2\), and \(−3\).

Rewrite division as multiplication by the reciprocal.

\(\frac{3x^{2}}{x+2}\cdot\frac{\left(x^{2}+5x+6\right)}{6x^{4}}\)

Factor the numerators and denominators.

\(\frac{3\cdot{x}\cdot{x}}{x+2}\cdot\frac{\left(x+2\right)\left(x+3\right)}{2\cdot3\cdot{x}\cdot{x}\cdot{x}\cdot{x}}\)

Simplify common factors

\(\large\frac{\cancel{3}\cdot{\cancel{x}}\cdot{\cancel{x}}}{\cancel{x+2}}\cdot\frac{\cancel{\left(x+2\right)}\left(x+3\right)}{2\cdot\cancel{3}\cdot{\cancel{x}}\cdot{\cancel{x}}\cdot{x}\cdot{x}}\)

Simplify.

\(\frac{(x+3)}{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/p[14]/span, line 1, column 2

}\)

Answer

\(\displaystyle \frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/div/p[1]/span[1], line 1, column 2

}{x+2}\div \frac{6

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/div/p[1]/span[2], line 1, column 2

}{(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/div/p[1]/span[3], line 1, column 2

+5x+6)}=\frac{x+3}{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[8]/div[4]/div/p[1]/span[4], line 1, column 2

}\).

The domain is all real numbers except 0, \(−3\).

[/hidden-answer]

Notice that once you rewrite the division as multiplication by a reciprocal, you follow the same process you used to multiply rational expressions.

In the video that follows, we present another example of dividing rational expressions.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Add and Subtract Rational Expressions

In beginning math, students usually learn how to add and subtract whole numbers before they are taught multiplication and division. However, with fractions and rational expressions, multiplication and division are sometimes taught first because these operations are easier to perform than addition and subtraction. Addition and subtraction of rational expressions are not as easy to perform as multiplication because, as with numeric fractions, the process involves finding common denominators. By working carefully and writing down the steps along the way, you can keep track of all of the numbers and variables and perform the operations accurately.

Add and Subtract

Adding and Subtracting Rational Expressions with Like Denominators

Adding rational expressions with the same denominator is the simplest place to start, so let’s begin there.

To add fractions with like denominators, add the numerators and keep the same denominator. Then simplify the sum. You know how to do this with numeric fractions.

\(\begin{array}{c}\frac{2}{9}+\frac{4}{9}=\frac{6}{9}\\\\\frac{6}{9}=\frac{3\cdot 2}{3\cdot 3}=\frac{3}{3}\cdot \frac{2}{3}=1\cdot \frac{2}{3}=\frac{2}{3}\end{array}\)

Follow the same process to add rational expressions with like denominators. Let’s try one.

Example

Add \(\displaystyle \frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[10]/div[1]/p[1]/span, line 1, column 2

}{x+4}+\frac{8x}{x+4}\), and define the domain.

State the sum in simplest form.

[reveal-answer q=”324146″]Show Solution[/reveal-answer]
[hidden-answer a=”324146″]

Since the denominators are the same, add the numerators.

\(\frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[10]/div[1]/p[5]/span, line 1, column 2

+8x}{x+4}\)

Factor the numerator.

\(\frac{2x(x+4)}{x+4}\)

Simplify common factors and.

\(\large\begin{array}{c}\frac{2x\cancel{(x+4)}}{\cancel{x+4}}\\\\=\frac{2x}{1}\end{array}\)

The domain is found by setting the denominators in the original sum equal to zero.

\(\begin{array}{l}x+4=0\\x=-4\end{array}\)

The domain is \(x\ne-4\)

Answer

\(\displaystyle \frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[10]/div[1]/div/p[1]/span, line 1, column 2

}{x+4}+\frac{8x}{x+4}=2x,x\ne -4\)

[/hidden-answer]

\(x\ne-4\). If we were to have defined the domain after simplifying, we would find that the domain is all real numbers which is incorrect.

To subtract rational expressions with like denominators, follow the same process you use to subtract fractions with like denominators. The process is just like the addition of rational expressions, except that you subtract instead of add.

Example

Subtract\(\frac{4x+7}{x+6}-\frac{2x+8}{x+6}\), and define the domain.

State the difference in simplest form.

[reveal-answer q=”681427″]Show Solution[/reveal-answer]
[hidden-answer a=”681427″]

Subtract the second numerator from the first and keep the denominator the same.

\(\frac{4x+7-(2x+8)}{x+6}\)

Be careful to distribute the negative to both terms of the second numerator.

\(\frac{4x+7-2x-8}{x+6}\)

Combine like terms. This rational expression cannot be simplified any further.

\(\frac{2x-1}{x+6}\)

The domain is found from the denominators of original expression.

\(\begin{array}{l}x+6=0\\x=-6\end{array}\)

The domain is \(x\ne-6\)

Answer

\(\displaystyle \frac{4x+7}{x+6}-\frac{2x+8}{x+6}=\frac{2x-1}{x+6},\text{}x\ne-6\)

[/hidden-answer]

In the video that follows, we present more examples of adding rational expressions with like denominators. Additionally, we review finding the domain of a rational expression.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Adding and Subtracting Rational Expressions with Unlike Denominators

What do they have in common?

Before adding and subtracting rational expressions with unlike denominators, you need to find a common denominator. Once again, this process is similar to the one used for adding and subtracting numeric fractions with unlike denominators. Remember how to do this?

\(\displaystyle \frac{5}{6}+\frac{8}{10}+\frac{3}{4}\)

Since the denominators are 6, 10, and 4, you want to find the least common denominator and express each fraction with this denominator before adding. (BTW, you can add fractions by finding any common denominator; it does not have to be the least. You focus on using the least because then there is less simplifying to do. But either way works.)

Finding the least common denominator is the same as finding the least common multiple of 4, 6, and 10. There are a couple of ways to do this. The first is to list the multiples of each number and determine which multiples they have in common. The least of these numbers will be the least common denominator.

Number	Multiples
4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64
6	12	18	24	30	36	42	48	54	60	66	68
10	20	30	40	50	60	70	80

The other method is to use prime factorization, the process of finding the prime factors of a number. This is how the method works with numbers.

Example

Use prime factorization to find the least common multiple of 6, 10, and 4.

[reveal-answer q=”371893″]Show Solution[/reveal-answer]
[hidden-answer a=”371893″]First, find the prime factorization of each denominator.

\(\begin{array}{r}6=3\cdot2\\10=5\cdot2\\4=2\cdot2\end{array}\)

The LCM will contain factors of 2, 3, and 5. Multiply each number the maximum number of times it appears in a single factorization.

In this case, 3 appears once, 5 appears once, and 2 is used twice because it appears twice in the prime factorization of 4.

Therefore, the LCM of 6, 10, and 4 is \(3\cdot5\cdot2\cdot2\), or 60.

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,6=3\cdot2\\\,\,\,\,\,\,\,\,10=5\cdot2\\\,\,\,\,\,\,\,\,\,\,\,4=2\cdot2\\\text{LCM}=3\cdot5\cdot2\cdot2\end{array}\)

Answer

The least common multiple of 6, 10, and 4 is 60.

[/hidden-answer]

Both methods give the same result, but prime factorization is faster. Your choice!

Now that you have found the least common multiple, you can use that number as the least common denominator of the fractions. Multiply each fraction by the fractional form of 1 that will produce a denominator of 60:

\(\begin{array}{r}\frac{5}{6}\cdot \frac{10}{10}=\frac{50}{60}\\\\\frac{8}{10}\cdot\frac{6}{6}=\frac{48}{60}\\\\\frac{3}{4}\cdot\frac{15}{15}=\frac{45}{60}\end{array}\)

Now that you have like denominators, add the fractions:

\(\frac{50}{60}+\frac{48}{60}+\frac{45}{60}=\frac{143}{60}\)

In the next example, we show how to find the least common multiple of a rational expression with a monomial in the denominator.

Example

Add\(\frac{2n}{15m^{2}}+\frac{3n}{21m}\), and give the domain.

State the sum in simplest form.

[reveal-answer q=”926091″]Show Solution[/reveal-answer]
[hidden-answer a=”926091″]

Find the prime factorization of each denominator.

\(\begin{array}{l}15m^{2}\,=\,3\cdot5\cdot{m}\cdot{m}\\\,\,\,21m\,=\,3\cdot7\cdot{m}\end{array}\)

Find the least common multiple. 3 appears exactly once in both of the expressions, so it will appear once in the least common multiple. Both 5 and 7 appear at most once. For the variables, the most m appears is twice.

Use the least common multiple for your new common denominator, it will be the LCD.

\(\begin{array}{l}15m^{2}\,=\,3\cdot5\cdot{m}\cdot{m}\\21m\,\,\,=\,3\cdot7\cdot{m}\\\text{LCM}:3\cdot5\cdot7\cdot{m}\cdot{m}\\\text{LCM}:105m^{2}\end{array}\)

Compare each original denominator and the new common denominator. Now rewrite the rational expressions to each have the common denominator of \(105m^{2}\). Remember that m cannot be 0 because the denominators would be 0.

The first denominator is \(105m^{2}\). You need to multiply \(\frac{7}{7}\).

The second denominator is \(105m^{2}\). You need to multiply \(5m\) to get the LCD, so multiply the entire rational expression by \(\frac{5m}{5m}\).

\(\begin{array}{c}\frac{2n}{15m^{2}}\cdot\frac{7}{7}=\frac{14n}{105m^{2}}\\\\\frac{3n}{21m}\cdot\frac{5m}{5m}=\frac{15mn}{105m^{2}}\end{array}\)

Add the numerators and keep the denominator the same.

\(\frac{14n}{105

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/p[14]/span[1], line 1, column 2

}+\frac{15mn}{105

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/p[14]/span[2], line 1, column 2

}=\frac{14n+15mn}{105

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/p[14]/span[3], line 1, column 2

}\)

If possible, simplify by finding common factors in the numerator and denominator. This rational expression is already in simplest form because the numerator and denominator have no factors in common.

\(\displaystyle \frac{n(14+15m)}{105

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/p[16]/span, line 1, column 2

}\)

Answer

\(\displaystyle \frac{2n}{15

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/div/p[1]/span[1], line 1, column 2

}+\frac{3n}{21m}=\frac{n(14+15m)}{105

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[3]/div/p[1]/span[2], line 1, column 2

},m\ne 0\)

[/hidden-answer]

That took a while, but you got through it. Adding rational expressions can be a lengthy process, but taken one step at a time, it can be done.

Now let’s try subtracting rational expressions. You’ll use the same basic technique of finding the least common denominator and rewriting each rational expression to have that denominator.

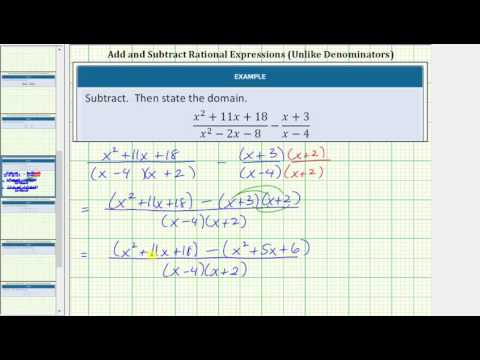
Example

Subtract\(\frac{2}{t+1}-\frac{t-2}{{{t}^{2}}-t-2}\), define the domain.

State the difference in simplest form.

[reveal-answer q=”704185″]Show Solution[/reveal-answer]
[hidden-answer a=”704185″]

Find the prime factorization of each denominator. \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[4]/p[4]/span, line 1, column 2

-t-2\) can be. Remember that t cannot be \(2\) because the denominators would be 0.

\(\begin{array}{c}t+1=t+1\\t^{2}-t-2=\left(t-2\right)\left(t+1\right)\end{array}\)

Find the least common multiple. \(t–2\) also appears once.

This means that \(\left(t-2\right)\left(t+1\right)\) is the least common multiple. In this case, it is easier to leave the common multiple in terms of the factors, so you will not multiply it out.

Use the least common multiple for your new common denominator, it will be the LCD.

\(\begin{array}{c}t+1=t+1\\t^{2}-t-2=\left(t-2\right)\left(t+1\right)\\\text{LCM}:\left(t+1\right)\left(t-1\right)\end{array}\)

Compare each original denominator and the new common denominator. Now rewrite the rational expressions to each have the common denominator of \(\left(t+1\right)\left(t–2\right)\).

You need to multiply \(t–2\) to get the LCD, so multiply the entire rational expression by \(\displaystyle \frac{t-2}{t-2}\).

The second expression already has a denominator of \(\left(t+1\right)\left(t–2\right)\), so you do not need to multiply it by anything.

\(\begin{array}{c}\frac{2}{t+1}\cdot \frac{t-2}{t-2}=\frac{2(t-2)}{(t+1)(t-2)}\\\\\,\,\,\frac{t-2}{{{t}^{2}}-t-2}=\frac{t-2}{(t+1)(t-2)}\end{array}\)

Then rewrite the subtraction problem with the common denominator.

\(\frac{2\left(t-2\right)}{\left(t+1\right)\left(t-2\right)}-\frac{t-2}{\left(t+1\right)\left(t-2\right)}\)

Subtract the numerators and simplify. Remember that parentheses need to be included around the second \(\left(t–2\right)\) in the numerator because the whole quantity is subtracted. Otherwise you would be subtracting just the t.

\(\begin{array}{c}\frac{2(t-2)-(t-2)}{(t+1)(t-2)}\\\\\frac{2t-4-t+2}{(t+1)(t-2)}\\\\\frac{t-2}{(t+1)(t-2)}\end{array}\)

The numerator and denominator have a common factor of \(t–2\), so the rational expression can be simplified.

\(\large\begin{array}{c}\frac{\cancel{t-2}}{(t+1)\cancel{(t-2)}}\\\\=\frac{1}{t+1}\end{array}\)

Answer

\(\displaystyle \frac{2}{t+1}-\frac{t-2}{{{t}^{2}}-t-2}=\frac{1}{t+1},t\ne -1,2\)

[/hidden-answer]

The video that follows contains an example of adding rational expressions whose denominators are not alike. The denominators of both expressions contain only monomials.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

The video that follows contains an example of subtracting rational expressions whose denominators are not alike. The denominators are a trinomial and a binomial.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Add rational expressions whose denominators have no common factors

So far all the rational expressions you’ve added and subtracted have shared some factors. What happens when they don’t have factors in common?

No Common Factors

In the next example, we show how to find a common denominator when there are no common factors in the expressions.

Example

Subtract \(\displaystyle \frac{3y}{2y-1}-\frac{4}{y-5}\), and give the domain.

State the difference in simplest form.

[reveal-answer q=”699142″]Show Solution[/reveal-answer]
[hidden-answer a=”699142″]

Neither \(y–5\) can be factored. Because they have no common factors, the least common multiple, which will become the least common denominator, is the product of these denominators.

\(\text{LCM}=\left(2y-1\right)\left(y-5\right)\)

Multiply each expression by the equivalent of 1 that will give it the common denominator.

Then rewrite the subtraction problem with the common denominator. It makes sense to keep the denominator in factored form in order to check for common factors.

\(\begin{array}{c}\frac{3y}{2y-1}\cdot \frac{y-5}{y-5}=\frac{3y(y-5)}{(2y-1)(y-5)}\\\\\frac{4}{y-5}\cdot \frac{2y-1}{2y-1}=\frac{4(2y-1)}{(2y-1)(y-5)}\\\\\frac{3y(y-5)}{(2y-1)(y-5)}-\frac{4(2y-1)}{(2y-1)(y-5)}\end{array}\)

Subtract and simplify.

\(\begin{array}{c}\frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[6]/p[10]/span[1], line 1, column 2

-15y}{(2y-1)(y-5)}-\frac{8y-4}{(2y-1)(y-5)}\\\\\frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[6]/p[10]/span[2], line 1, column 2

-15y-(8y-4)}{(2y-1)(y-5)}\\\\\frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[6]/p[10]/span[3], line 1, column 2

-15y-8y+4}{(2y-1)(y-5)}\end{array}\)

The domain is found by setting the original denominators equal to zero.

\(\begin{array}{l}2y-1=0\text{ and }y-5=0\\\,\,\,y=\frac{1}{2}\,\,\,\,\,\,\,\text{ and }y=5\end{array}\)

The domain is \(y\ne\frac{1}{2}, y\ne5\)

Answer

\(\displaystyle \frac{3y}{2y-1}-\frac{4}{y-5}=\frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[6]/div/p[1]/span[1], line 1, column 2

-23y+4}{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[6]/div/p[1]/span[2], line 1, column 2

-11y+5},y\ne \frac{1}{2},5\)

[/hidden-answer]

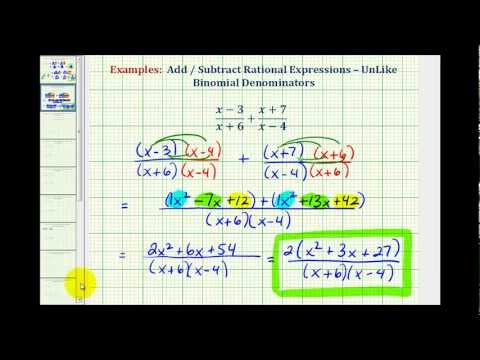
In the video that follows, we present an example of adding two rational expression whose denominators are binomials with no common factors.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

You may need to combine more than two rational expressions. While this may seem pretty straightforward if they all have the same denominator, what happens if they do not?

In the example below, notice how a common denominator is found for three rational expressions. Once that is done, the addition and subtraction of the terms looks the same as earlier, when you were only dealing with two terms.

Example

Simplify\(\frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[1]/span, line 1, column 2

}{{{x}^{2}}-4}+\frac{x}{x-2}-\frac{1}{x+2}\), and give the domain.

State the result in simplest form.

[reveal-answer q=”47691″]Show Solution[/reveal-answer]
[hidden-answer a=”47691″]

Find the least common multiple by factoring each denominator. Multiply each factor the maximum number of times it appears in a single factorization. Remember that x cannot be \(-2\) because the denominators would be 0.

\(\left(x–2\right)\). This means the LCM is \(\left(x+2\right)\left(x–2\right)\).

\(\begin{array}{l}x^{2}-4=\left(x+2\right)\left(x-2\right)\\\,\,x-2=x-2\\\,\,x+2=x+2\\\,\,\text{LCM}=\left(x+2\right)\left(x-2\right)\end{array}\)

The LCM becomes the common denominator.

Multiply each expression by the equivalent of 1 that will give it the common denominator.

\(\begin{array}{r}\frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[9]/span[1], line 1, column 2

}

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[9]/span[2], line 1, column 3

{(x+2)(x-2)}\\\frac{x}{x-2}\cdot \frac{x+2}{x+2}=\frac{x(x+2)}{(x+2)(x-2)}\\\frac{1}{x+2}\cdot \frac{x-2}{x-2}=\frac{1(x-2)}{(x+2)(x-2)}\end{array}\)

Rewrite the original problem with the common denominator. It makes sense to keep the denominator in factored form in order to check for common factors.

\(\displaystyle \frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[11]/span, line 1, column 2

}{(x+2)(x-2)}+\frac{x(x+2)}{(x+2)(x-2)}-\frac{1(x-2)}{(x+2)(x-2)}\)

Combine the numerators.

\(\begin{array}{c}\frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[13]/span[1], line 1, column 2

+x(x+2)-1(x-2)}{(x+2)(x-2)}\\\\\frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[13]/span[2], line 1, column 2

+

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[13]/span[3], line 1, column 2

+2x-x+2}{(x+2)(x-2)}\end{array}\)

Check for simplest form. Since neither \(\left(x-2\right)\) is a factor of \(3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[14]/span, line 1, column 2

+x+2\), this expression is in simplest form.

\(\frac{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/p[15]/span, line 1, column 2

+x+2}{(x+2)(x-2)}\)

Answer

\(\displaystyle \frac{2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[7]/div/p[1]/span, line 1, column 2

}{{{x}^{2}}-4}+\frac{x}{x-2}-\frac{1}{x+2}=\frac{3{{x}^{2}}+x+2}{(x+2)(x-2)}\) \(\displaystyle x\ne 2,-2\)

[/hidden-answer]

In the video that follows we present an example of subtracting 3 rational expressions with unlike denominators. One of the terms being subtracted is a number, so the denominator is 1.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Example

Simplify\(\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/p[1]/span, line 1, column 3

{3y}-\frac{2}{x}-\frac{15}{9}\), and give the domain.

State the result in simplest form.

[reveal-answer q=”77199″]Show Solution[/reveal-answer]
[hidden-answer a=”77199″]

Find the least common multiple by factoring each denominator. Multiply each factor the maximum number of times it appears in a single factorization.

\(\begin{array}{l}\,\,\,\,\,\,\,\,3y=3\cdot{y}\\\,\,\,\,\,\,\,\,\,\,x=x\\\,\,\,\,\,\,\,\,\,\,9=3\cdot3\\\text{LCM}=3\cdot3\cdot{x}\cdot{y}\\\text{LCM}=9xy\end{array}\)

The LCM becomes the common denominator. Multiply each expression by the equivalent of 1 that will give it the common denominator.

\(\begin{array}{r}\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/p[7]/span[1], line 1, column 3

{3y}\cdot \frac{3x}{3x}=\frac{3x

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/p[7]/span[2], line 1, column 2

}{9xy}\\\\\frac{2}{x}\cdot \frac{9y}{9y}=\frac{18y}{9xy}\,\,\\\\\frac{15}{9}\cdot \frac{xy}{xy}=\frac{15xy}{9xy}\end{array}\)

Rewrite the original problem with the common denominator.

\(\frac{3x

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/p[9]/span, line 1, column 2

}{9xy}-\frac{18y}{9xy}-\frac{15xy}{9xy}\)

Combine the numerators.

\(\frac{3x

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/p[11]/span, line 1, column 2

-18y-15xy}{9xy}\)

Check for simplest form.

\(\large\begin{array}{c}\frac{3y(xy-6-5x)}{9xy}\\\\=\frac{3y(xy-6-5x)}{3y(3x)}\\\\=\frac{\cancel{3y}(xy-6-5x)}{\cancel{3y}(3x)}\\\\=\frac{xy-6-5x}{3x}\end{array}\)

The domain is found by setting the denominators equal to zero. \(9=0\) is nonsense, so we don’t need to worry about that denominator.

\(\begin{array}{l}3y=0\text{ and }x=0\\y=0\text{ and }x=0\end{array}\)

The domain is \(y\ne0, x\ne0\)

Answer

\(\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.03:_Operations_on_Rational_Expressions), /content/body/div[11]/div[8]/div/p[1]/span, line 1, column 3

{3y}-\frac{2}{x}-\frac{15}{9}=\frac{xy-5x-6}{3x},y\ne 0,x\ne 0\)

[/hidden-answer]

In this last video, we present another example of adding and subtracting three rational expressions with unlike denominators.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=130

Add and Subtract

Summary

In the next sections we will introduce some techniques for solving rational equations. The methods shown here will help you when you are solving rational equations. To add and subtract rational expressions that share common factors, you first identify which factors are missing from each expression, and build the LCD with them. To add and subtract rational expressions with no common factors, the LCD will be the product of all the factors of the denominators.

Summary

Rational expressions are multiplied and divided the same way as numeric fractions. To multiply, first find the greatest common factors of the numerator and denominator. Next, regroup the factors to make fractions equivalent to one. Then, multiply any remaining factors. To divide, first rewrite the division as multiplication by the reciprocal of the denominator. The steps are then the same as for multiplication.

When expressing a product or quotient, it is important to state the excluded values. These are all values of a variable that would make a denominator equal zero at any step in the calculations.

CC licensed content, Original

• Screenshot: Multiply and Divide. Provided by: Lumen Learning. License: CC BY: Attribution
• Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
• Screenshot: Reciprocal Architecture. Provided by: Lumen Learning. License: CC BY: Attribution
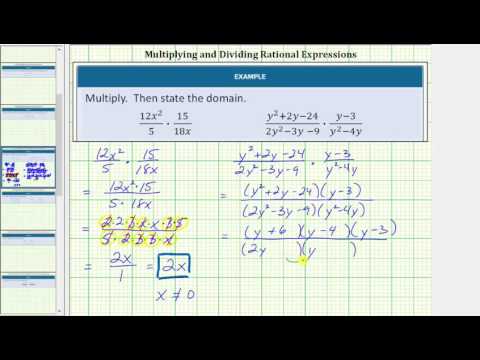
• Multiply Rational Expressions and Give the Domain. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/Hj6gF1SNttk. License: CC BY: Attribution
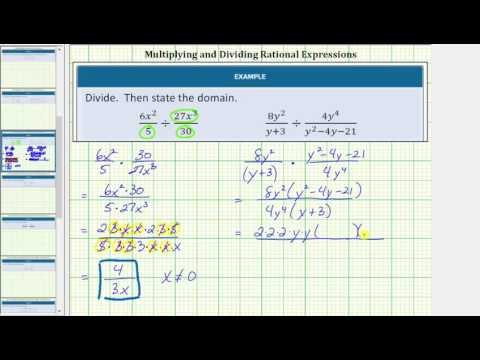
• Divide Rational Expressions and Give the Domain. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/B1tigfgs268. License: CC BY: Attribution
• Graphic: No common factors.. Provided by: Lumen Learning. License: CC BY: Attribution
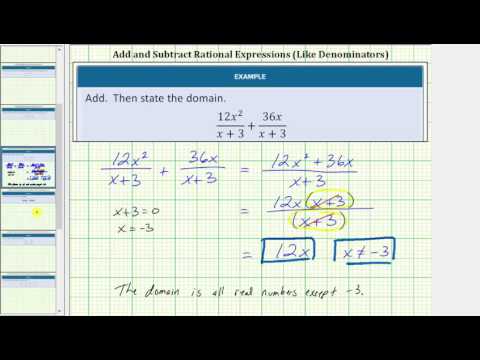
• Screenshot: Add and subtract. Provided by: Lumen Learning. License: CC BY: Attribution
• Subtract Rational Expressions with UnLike Denominators - 3 Expressions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/c-8xQyU0ch0. License: CC BY: Attribution
• Add and Subtract Rational Expressions with UnLike Denominators - 3 Expressions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/43xPStLm39A. License: CC BY: Attribution

CC licensed content, Shared previously

• Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
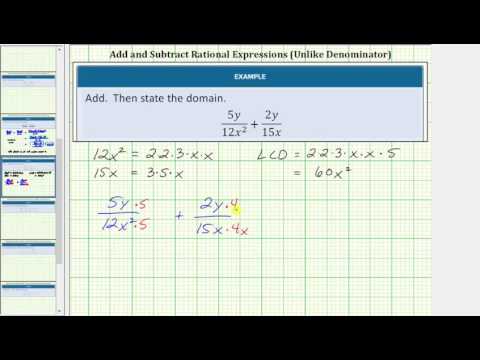
• Ex: Add Rational Expressions with Unlike Denominators. Authored by: James Sousa (Mathispower4u.com) . Located at: https://www.youtube.com/watch?v=CKGpiTE5vIg&feature=youtu.be. License: CC BY: Attribution