7.4: Solve Rational Equations
- Page ID
- 51477
Learning Objectives
- Solve rational equations
- Solve rational equations by clearing denominators
- Identify extraneous solutions in a rational equation
- Solve for a variable in a rational formula
- Applications of rational equations
- Identify the components of a work equation
- Solve a work equation
- Define and write a proportion
- Solve proportional problems involving scale drawings
- Define direct variation, and solve problems involving direct variation
- Define inverse variation and solve problems involving inverse variation
- Define joint variation and solve problems involving joint variation
Equations that contain rational expressions are called rational equations. For example, \(\frac{2x+1}{4}=\frac{x}{3}\) is a rational equation. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing a variety of proportional relationships.
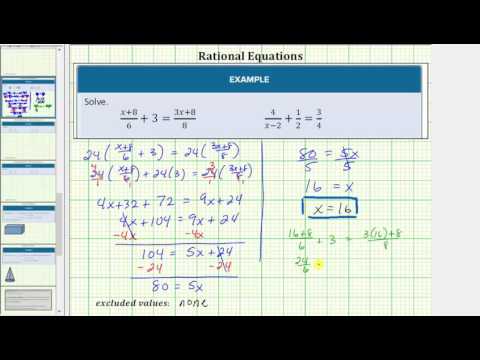
One of the most straightforward ways to solve a rational equation is to eliminate denominators with the common denominator, then use properties of equality to isolate the variable. This method is often used to solve linear equations that involve fractions as in the following example:
Solve \(\frac{1}{2}x-3=2-\frac{3}{4}x\) by clearing the fractions in the equation first.
Multiply both sides of the equation by 4, the common denominator of the fractional coefficients.
\(\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)+4\left(-\frac{3}{4}x\right)\\2x-12=8-3x\\\underline{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{array}\)
We could have found a common denominator and worked with fractions, but that often leads to more mistakes. We can apply the same idea to solving rational equations. The difference between a linear equation and a rational equation is that rational equations can have polynomials in the numerator and denominator of the fractions. This means that clearing the denominator may sometimes mean multiplying the whole rational equation by a polynomial. In the next example, we will clear the denominators of a rational equation with a terms that has a polynomial in the numerator.
Example
Solve the equation \(2\cdot2\cdot2\), or 8, will be the LCM.
\(\begin{array}{l}4=2\cdot2\\8=2\cdot2\cdot2\cdot2\\\text{LCM}=2\cdot2\cdot2\\\text{LCM}=8\end{array}\)
The LCM of 4 and 8 is also the lowest common denominator for the two fractions.
Multiply both sides of the equation by the common denominator, 8, to keep the equation balanced and to eliminate the denominators.
\(\begin{array}{r}8\cdot \frac{x+5}{8}=\frac{7}{4}\cdot 8\,\,\,\,\,\,\,\\\\\frac{8(x+5)}{8}=\frac{7(8)}{4}\,\,\,\,\,\,\\\\\frac{8}{8}\cdot (x+5)=\frac{7(4\cdot 2)}{4}\\\\\frac{8}{8}\cdot (x+5)=7\cdot 2\cdot \frac{4}{4}\\\\1\cdot (x+5)=14\cdot 1\,\,\,\end{array}\)
Simplify and solve for x.
\(\begin{array}{r}x+5=14\\x=9\,\,\,\end{array}\)
Check the solution by substituting 9 for x in the original equation.
\(\begin{array}{r}\frac{x+5}{8}=\frac{7}{4}\\\\\frac{9+5}{8}=\frac{7}{4}\\\\\frac{14}{8}=\frac{7}{4}\\\\\frac{7}{4}=\frac{7}{4}\end{array}\)
Answer
\(x=9\)
[/hidden-answer]
In the next example, we show how to solve a rational equation with a binomial in the denominator of one term. We will use the common denominator to eliminate the denominators from both fractions. Note that the LCD is the product of both denominators because they don’t share any common factors.
Example
Solve the equation \(\frac{8}{x+1}=\frac{4}{3}\).
[reveal-answer q=”331190″]Show Solution[/reveal-answer]
[hidden-answer a=”331190″]Clear the denominators by multiplying each side by the common denominator. The common denominator is \(3\text{ and }x+1\) don’t have any common factors.
\(\begin{array}{c}3\left(x+1\right)\left(\frac{8}{x+1}\right)=3\left(x+1\right)\left(\frac{4}{3}\right)\end{array}\)
Simplify common factors.
\(\begin{array}{c}3\cancel{\left(x+1\right)}\left(\frac{8}{\cancel{x+1}}\right)=\cancel{3}\left(x+1\right)\left(\frac{4}{\cancel{3}}\right)\\24=4\left(x+1\right)\\24=4x+4\end{array}\)
Now this looks like a linear equation, and we can use the addition and multiplication properties of equality to solve it.
\(\begin{array}{c}24=4x+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\20=4x\,\,\,\,\,\,\,\,\\\\x=5\,\,\,\,\,\,\,\,\,\end{array}\)
Check the solution in the original equation.
\(\begin{array}{r}\,\,\,\,\,\frac{8}{\left(x+1\right)}=\frac{4}{3}\\\\\frac{8}{\left(5+1\right)}=\frac{4}{3}\\\\\frac{8}{6}=\frac{4}{3}\end{array}\)
Reduce the fraction \(\frac{8}{6}\) by simplifying the common factor of 2:
\(\large\frac{\cancel{2}\cdot4}{\cancel{2}\cdot3}\normalsize=\large\frac{4}{3}\)
Answer
\(x=1\)
[/hidden-answer]
You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.
Example
Solve the equation \(\frac{x}{3}+1=\frac{4}{3}\).
[reveal-answer q=”950823″]Show Solution[/reveal-answer]
[hidden-answer a=”950823″]Both fractions in the equation have a denominator of 3. Multiply both sides of the equation (not just the fractions!) by 3 to eliminate the denominators.
\(3\left( \frac{x}{3}+1 \right)=3\left( \frac{4}{3} \right)\)
Apply the distributive property and multiply 3 by each term within the parentheses. Then simplify and solve for x.
\(\begin{array}{r}3\left( \frac{x}{3} \right)+3\left( 1 \right)=3\left( \frac{4}{3} \right)\\\\\cancel{3}\left( \frac{x}{\cancel{3}} \right)+3\left( 1 \right)=\cancel{3}\left( \frac{4}{\cancel{3}} \right)\\\\ x+3=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-3}\,\,\,\,\,\underline{-3}\\\\x=1\end{array}\)
Answer
\(x=1\)
[/hidden-answer]
In the video that follows we present two ways to solve rational equations with both integer and variable denominators.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
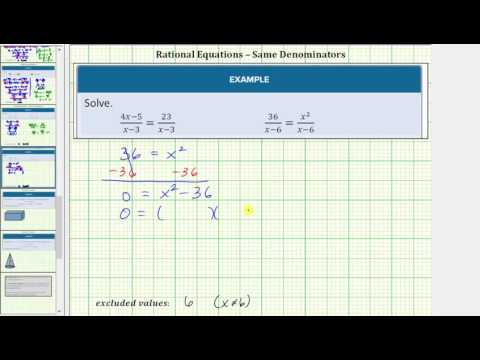
Excluded Values and Extraneous Solutions
Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values. Let’s look at an example.
Example
Solve the equation \(\frac{2x-5}{x-5}=\frac{15}{x-5}\).
[reveal-answer q=”266674″]Show Solution[/reveal-answer]
[hidden-answer a=”266674″]Determine any values for x that would make the denominator 0.
\(\frac{2x-5}{x-5}=\frac{15}{x-5}\)
5 is an excluded value because it makes the denominator \(x-5\) equal to 0.
Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for x.
\(\begin{array}{r}2x-5=15\\2x=20\\x=10\end{array}\)
Check the solution in the original equation.
\(\begin{array}{r}\frac{2x-5}{x-5}=\frac{15}{x-5}\,\,\\\\\frac{2(10)-5}{10-5}=\frac{15}{10-5}\\\\\frac{20-5}{10-5}=\frac{15}{10-5}\\\\\frac{15}{5}=\frac{15}{5}\,\,\,\,\,\,\,\,\,\end{array}\)
Answer
\(x=10\)
[/hidden-answer]
In the following video we present an example of solving a rational equation with variables in the denominator.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions. That’s why it is always important to check all solutions in the original equations—you may find that they yield untrue statements or produce undefined expressions.
Example
Solve the equation \(\frac{16}{m+4}=\frac
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[1]/span, line 1, column 3
[reveal-answer q=”450589″]Show Solution[/reveal-answer]
[hidden-answer a=”450589″]Determine any values for m that would make the denominator 0. \(m+4\) equal to 0.
Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for m.
\(\begin{array}{l}16=m^{2}\\\,\,\,0=
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[4]/span, line 1, column 2
\(\begin{array}{c}0=m+4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,0=m-4\\m=-4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,m=4\\m=4,-4\end{array}\)
Check the solutions in the original equation.
Since \(m=−4\) leads to division by 0, it is an extraneous solution.
\(\begin{array}{c}\frac{16}{m+4}=\frac
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[8]/span[1], line 1, column 3
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[8]/span[2], line 1, column 6
\(-4\) is excluded because it leads to division by 0.
\(\begin{array}{c}\frac{16}{4+4}=\frac
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[10]/span, line 1, column 5
Answer
\(m=4\)
[/hidden-answer]
Rational formulas
Rational formulas can be useful tools for representing real-life situations and for finding answers to real problems. Equations representing direct, inverse, and joint variation are examples of rational formulas that can model many real-life situations. As you will see, if you can find a formula, you can usually make sense of a situation.
When solving problems using rational formulas, it is often helpful to first solve the formula for the specified variable. For example, work problems ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, \(W=rt\). The amount of work done (W) is the product of the rate of work (r) and the time spent working (t). Using algebra, you can write the work formula 3 ways:
\(W=rt\)
Find the time (t): \(t=\frac{W}{r}\)(divide both sides by r)
Find the rate (r): \(r=\frac{W}{t}\)(divide both sides by t)
Example
The formula for finding the density of an object is \(D=\frac{m}{v}\), where D is the density, m is the mass of the object and v is the volume of the object. Rearrange the formula to solve for the mass (m) and then for the volume (v).
[reveal-answer q=”537110″]Show Solution[/reveal-answer]
[hidden-answer a=”537110″]Start with the formula for density.
\(D=\frac{m}{v}\)
Multiply both side of the equation by v to isolate m.
\(v\cdot D=\frac{m}{v}\cdot v\)
Simplify and rewrite the equation, solving for m.
\(\begin{array}{l}v\cdot D=m\cdot \frac{v}{v}\\v\cdot D=m\cdot 1\\v\cdot D=m\end{array}\)
To solve the equation \(D=\frac{m}{v}\) in terms of v, you will need do the same steps to this point, and then divide both sides by D.
\(\begin{array}{r}\frac{v\cdot D}{D}=\frac{m}{D}\\\\\frac{D}{D}\cdot v=\frac{m}{D}\\\\1\cdot v=\frac{m}{D}\\\\v=\frac{m}{D}\end{array}\)
Answer
\(v=\frac{m}{D}\)
[/hidden-answer]
Now let’s look at an example using the formula for the volume of a cylinder.
Example
The formula for finding the volume of a cylinder is \(V=\pi{r^{2}}h\), where V is the volume, r is the radius and h is the height of the cylinder. Rearrange the formula to solve for the height (h).
[reveal-answer q=”644317″]Show Solution[/reveal-answer]
[hidden-answer a=”644317″]Start with the formula for the volume of a cylinder.
\(V=\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[3]/span, line 1, column 2
Divide both sides by \(\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[4]/span, line 1, column 2
\(\frac{V}{\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[2], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[3], line 1, column 2
Simplify. You find the height, h, is equal to \(\frac{V}{\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[6]/span, line 1, column 2
\(\frac{V}{\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[7]/span, line 1, column 2
Answer
\(h=\frac{V}{\pi
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/div/p[1]/span, line 1, column 2
[/hidden-answer]
In the following video we give another example of solving for a variable in a formula, or as they are also called, a literal equation.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Applications of Rational Equations
Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.
Work
A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, \(d=rt\).) The amount of work done (W) is the product of the rate of work (r) and the time spent working (t). The work formula has 3 versions.
\(\begin{array}{l}W=rt\\\\\,\,\,\,\,t=\frac{W}{r}\\\\\,\,\,\,\,r=\frac{W}{t}\end{array}\)
Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.
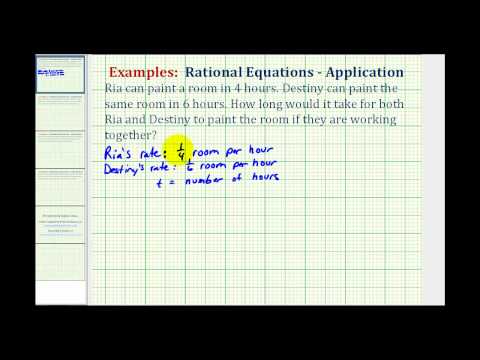
Example
Myra takes 2 hours to plant 50 flower bulbs. Francis takes 3 hours to plant 45 flower bulbs. Working together, how long should it take them to plant 150 bulbs?
[reveal-answer q=”550322″]Show Solution[/reveal-answer]
[hidden-answer a=”550322″]Think about how many bulbs each person can plant in one hour. This is their planting rate.
Myra: \(\frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}\)
Francis: \(\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}\)
Combine their hourly rates to determine the rate they work together.
Myra and Francis together:
\(\frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}+\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}=\frac{40\,\,\text{bulbs}}{1\,\,\text{hour}}\)
Use one of the work formulas to write a rational equation, for example \(r=\frac{W}{t}\). You know r, the combined work rate, and you know W, the amount of work that must be done. What you don’t know is how much time it will take to do the required work at the designated rate.
\(\frac{40}{1}=\frac{150}{t}\)
Solve the equation by multiplying both sides by the common denominator, then isolating t.
\(\begin{array}{c}\frac{40}{1}\cdot 1t=\frac{150}{t}\cdot 1t\\\\40t=150\\\\t=\frac{150}{40}=\frac{15}{4}\\\\t=3\frac{3}{4}\text{hours}\end{array}\)
Answer
It should take 3 hours 45 minutes for Myra and Francis to plant 150 bulbs together.
[/hidden-answer]
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.
Example
Joe and John are planning to paint a house together. John thinks that if he worked alone, it would take him 3 times as long as it would take Joe to paint the entire house. Working together, they can complete the job in 24 hours. How long would it take each of them, working alone, to complete the job?
[reveal-answer q=”593775″]Show Solution[/reveal-answer]
[hidden-answer a=”593775″]Choose variables to represent the unknowns. Since it takes John 3 times as long as Joe to paint the house, his time is represented as 3x.
Let x = time it takes Joe to complete the job
3x = time it takes John to complete the job
The work is painting 1 house or 1. Write an expression to represent each person’s rate using the formula \(r=\frac{W}{t}\).
Joe’s rate: \(\frac{1}{x}\)
John’s rate: \(\frac{1}{3x}\)
Their combined rate is the sum of their individual rates. Use this rate to write a new equation using the formula \(W=rt\).
combined rate: \(\frac{1}{x}+\frac{1}{3x}\)
The problem states that it takes them 24 hours together to paint a house, so if you multiply their combined hourly rate \(\left( \frac{1}{x}+\frac{1}{3x} \right)\) by 24, you will get 1, which is the number of houses they can paint in 24 hours.
\(\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\frac{24}{x}+\frac{24}{3x}\end{array}\)
Now solve the equation for x. (Remember that x represents the number of hours it will take Joe to finish the job.)
\(\begin{array}{l}\,\,\,1=\frac{3}{3}\cdot \frac{24}{x}+\frac{24}{3x}\\\\\,\,\,1=\frac{3\cdot 24}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72+24}{3x}\\\\\,\,\,1=\frac{96}{3x}\\\\3x=96\\\\\,\,\,x=32\end{array}\)
Check the solutions in the original equation.
\(\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\left[ \frac{\text{1}}{\text{32}}+\frac{1}{3\text{(32})} \right]24\\\\1=\frac{24}{\text{32}}+\frac{24}{3\text{(32})}\\\\1=\frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{3}{3}\cdot \frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{72}{96}+\frac{24}{96}[\end{array}\)
The solution checks. Since \(x=32\), it takes Joe 32 hours to paint the house by himself. John’s time is 3x, so it would take him 96 hours to do the same amount of work.
Answer
It takes 32 hours for Joe to paint the house by himself and 96 hours for John the paint the house himself.
[/hidden-answer]
In the video that follows, we show another example of finding one person’s work rate given a combined work rate.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
As shown above, many work problems can be represented by the equation \(\frac{t}{a}+\frac{t}{b}=1\), where t is the time to do the job together, a is the time it takes person A to do the job, and b is the time it takes person B to do the job. The 1 refers to the total work done—in this case, the work was to paint 1 house.
The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t, set it equal to the amount of work done, and solve the rational equation.
We present another example of two people painting at different rates in the following video.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Proportions
A proportion is a statement that two ratios are equal to each other. There are many things that can be represented with ratios, including the actual distance on the earth that is represented on a map. In fact, you probably use proportional reasoning on a regular basis and don’t realize it. For example, say you have volunteered to provide drinks for a community event. You are asked to bring enough drinks for 35-40 people. At the store you see that drinks come in packages of 12. You multiply 12 by 3 and get 36 – this may not be enough if 40 people show up, so you decide to buy 4 packages of drinks just to be sure.
This process can also be expressed as a proportional equation and solved using mathematical principles. First, we can express the number of drinks in a package as a ratio:
\(\frac{12\text{ drinks }}{1\text{ package }}\)
Then we express the number of people who we are buying drinks for as a ratio with the unknown number of packages we need. We will use the maximum so we have enough.
\(\frac{40\text{ people }}{x\text{ packages }}\)
We can find out how many packages to purchase by setting the expressions equal to each other:
\(\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\)
To solve for x, we can use techniques for solving linear equations, or we can cross multiply as a shortcut.
\(\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\\\text{}\\x\cdot\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{40}{12}=\frac{10}{3}=3.33\end{array}\)
We can round up to 4 since it doesn’t make sense to by 0.33 of a package of drinks. Of course, you don’t write out your thinking this way when you are in the grocery store, but doing so helps you to be able to apply the concepts to less obvious problems. In the following example we will show how to use a proportion to find the number of people on teh planet who don’t have access to a toilet.
Example
As of March, 2016 the world’s population was estimated at 7.4 billion. [1]. According to water.org, 1 out of every 3 people on the planet lives without access to a toilet. Find the number of people on the planet that do not have access to a toilet.
[reveal-answer q=”54118″]Show Solution[/reveal-answer]
[hidden-answer a=”54118″]
Read and Understand: We can use a proportion to find the unknown number of people who live without a toilet since we are given that 1 in 3 don’t have access, and we are given the population of the planet.
Define and Translate: We know that 1 out of every 3 people don’t have access, so we can write that as a ratio (fraction)
\(\frac{1\text{ doesn't }}{3\text{ do }}\).
Let the number of people without access to a toilet be x. The ratio of people with and without toilets is then
\(\frac{x\text{ don't }}{7.4\text{ billion do}}\)
Notice how it helps to use descriptions or units to know where to place the given numbers in the proportion.
Write and Solve: Equate the two ratios since they are representing the same fractional amount of the population.
\(\frac{1}{3}=\frac{x}{7.4\text{ billion }}\)
Solve:
\(\begin{array}{l}\frac{1}{3}=\frac{x}{7.4}\\\text{}\\7.4\cdot\frac{1}{3}=\frac{x}{7.4}\cdot{7.4}\\\text{}\\2.46=x\end{array}\)
Interpret: The original units were billions of people, so our answer is \(2.46\) billion people don’t have access to a toilet. Wow, that’s a lot of people.
Answer
2.46 billion people don’t have access to a toilet.
[/hidden-answer]
In the next example, we will use the length of a person’t femur to estimate their height. This process is used in forensic science and anthropology, and has been found in many scientific studies to be a very good estimate.
Example
It has been shown that a person’s height is proportional to the length of their femur [2]. Given that a person who is 71 inches tall has a femur length of 17.75 inches, how tall is someone with a femur length of 16 inches?
[reveal-answer q=”987898″]Show Solution[/reveal-answer]
[hidden-answer a=”987898″]
Read and Understand: Height and femur length are proportional for everyone, so we can define a ratio with the given height and femur length. We can then use this to write a proportion to find the unknown height.
Define and Translate: Let x be the unknown height. Define the ratio of femur length and height for both people using the given measurements.
Person 1: \(\frac{\text{femur length}}{\text{height}}=\frac{17.75\text{inches}}{71\text{inches}}\)
Person 2: \(\frac{\text{femur length}}{\text{height}}=\frac{16\text{inches}}{x\text{inches}}\)
Write and Solve: Equate the ratios, since we are assuming height and femur length are proportional for everyone.
\(\frac{17.75\text{inches}}{71\text{inches}}=\frac{16\text{inches}}{x\text{inches}}\)
Solve by using the common denominator to clear fractions. The common denominator is \(71x\)
\(\begin{array}{c}\frac{17.75}{71}=\frac{16}{x}\\\\71x\cdot\frac{17.75}{71}=\frac{16}{x}\cdot{71x}\\\\17.75\cdot{x}=16\cdot{71}\\\\x=\frac{16\cdot{71}}{17.75}=64\end{array}\)
Interpret: The unknown height of person 2 is 64 inches. In general, we can reduce the fraction \(\frac{17.75}{71}=0.25=\frac{1}{4}\) to find a general rule for everyone. This would translate to saying for every one femur length, a person’s height is 4 times that length.
[/hidden-answer]
Another way to describe the ratio of femur length to height that we found in the last example is to say there’s a 1:4 ratio between femur length and height, or 1 to 4.
Ratios are also used in scale drawings. Scale drawings are enlarged or reduced drawings of objects, buildings, roads, and maps. Maps are smaller than what they represent and a drawing of dendritic cells in your brain is most likely larger than what it represents. The scale of the drawing is a ratio that represents a comparison of the length of the actual object and it’s representation in the drawing. The image below shows a map of the us with a scale of 1 inch representing 557 miles. We could write the scale factor as a fraction \(\frac{1}{557}\) or as we did with the femur-height relationship, 1:557.
In the next example we will use the scale factor given in the image above to find the distance between Seattle Washington and San Jose California.
Example
Given a scale factor of 1:557 on a map of the US, if the distance from Seattle, WA to San Jose, CA is 1.5 inches on the map, define a proportion to find the actual distance between them.
[reveal-answer q=”936583″]Show Solution[/reveal-answer]
[hidden-answer a=”936583″]
Read and Understand: We need to define a proportion to solve for the unknown distance between Seattle and San Jose.
Define and Translate: The scale factor is 1:557, and we will call the unknown distance x. The ratio of inches to miles is \(\frac{1}{557}\).
We know inches between the two cities, but we don’t know miles, so the ratio that describes the distance between them is \(\frac{1.5}{x}\).
Write and Solve: The proportion that will help us solve this problem is \(\frac{1}{557}=\frac{1.5}{x}\).
Solve using the common denominator \(557x\) to clear fractions.
\(\begin{array}{c}\frac{1}{557}=\frac{1.5}{x}\\\\557x\cdot\frac{1}{557}=\frac{1.5}{x}\cdot{557x}\\\\x=1.5\cdot{557}=835.5\)
Interpret: We used the scale factor 1:557 to find an unknown distance between Seattle and San Jose. We also check our answer of 835.5 miles with Google maps, and found that the distance is 839.9 miles, so we did pretty well!
[/hidden-answer]
In the next example, we will find a scale factor given the length between two cities on a map, and their actual distance from each other.
Example
Two cities are 2.5 inches apart on a map. Their actual distance from each other is 325 miles. Write a proportion to represent and solve for the scale factor for one inch of the map.
[reveal-answer q=”151234″]Show Solution[/reveal-answer]
[hidden-answer a=”151234″]
Read and Understand: We know that for each 2.5 inches on the map, it represents 325 actual miles. We are looking for the scale factor for one inch of the map.
Define and Translate: The ratio we want is \(\frac{2.5}{325}\)
Write and Solve: We can use a proportion to equate the two ratios and solve for the unknown distance.
\(\begin{array}{c}\frac{1}{x}=\frac{2.5}{325}\\\\325x\cdot\frac{1}{x}=\frac{2.5}{325}\cdot{325x}\\\\325=2.5x\\\\x=130\)
Interpret: The scale factor for one inch on the map is 1:130, or for every inch of map there are 130 actual miles.
[/hidden-answer]
The video that follows show another example of finding an actual distance using the scale factor from a map.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
In the video that follows, we present an example of using proportions to obtain the correct amount of medication for a patient, as well as finding a desired mixture of coffees.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Variation
Direct Variation
Variation equations are examples of rational formulas and are used to describe the relationship between variables. For example, imagine a parking lot filled with cars. The total number of tires in the parking lot is dependent on the total number of cars. Algebraically, you can represent this relationship with an equation.
\(\text{number of tires}=4\cdot\text{number of cars}\)
The number 4 tells you the rate at which cars and tires are related. You call the rate the constant of variation. It’s a constant because this number does not change. Because the number of cars and the number of tires are linked by a constant, changes in the number of cars cause the number of tires to change in a proportional, steady way. This is an example of direct variation, where the number of tires varies directly with the number of cars.
You can use the car and tire equation as the basis for writing a general algebraic equation that will work for all examples of direct variation. In the example, the number of tires is the output, 4 is the constant, and the number of cars is the input. Let’s enter those generic terms into the equation. You get \(y=kx\). That’s the formula for all direct variation equations.
\(\text{number of tires}=4\cdot\text{number of cars}\\\text{output}=\text{constant}\cdot\text{input}\)
Example
Solve for k, the constant of variation, in a direct variation problem where \(x=10\).
[reveal-answer q=”714779″]Show Solution[/reveal-answer]
[hidden-answer a=”714779″]Write the formula for a direct variation relationship.
\(y=kx\)
Substitute known values into the equation.
\(300=k\left(10\right)\)
Solve for k by dividing both sides of the equation by 10.
\(\begin{array}{l}\frac{300}{10}=\frac{10k}{10}\\\\\,\,\,\,30=k\end{array}\)
Answer
The constant of variation, k, is 30.
[/hidden-answer]
In the video that follows, we present an example of solving a direct variation equation.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Inverse Variation
Another kind of variation is called inverse variation. In these equations, the output equals a constant divided by the input variable that is changing. In symbolic form, this is the equation \(y=\frac{k}{x}\).
One example of an inverse variation is the speed required to travel between two cities in a given amount of time.
Let’s say you need to drive from Boston to Chicago, which is about 1,000 miles. The more time you have, the slower you can go. If you want to get there in 20 hours, you need to go 50 miles per hour (assuming you don’t stop driving!), because \(\frac{1,000}{40}=25\).
The equation for figuring out how fast to travel from the amount of time you have is \(d=rt\). If you solve \(r=\frac{d}{t}\), or \(speed=\frac{miles}{time}\).
In the case of the Boston to Chicago trip, you can write \(y=\frac{k}{x}\).
Example
Solve for k, the constant of variation, in an inverse variation problem where \(y=25\).
[reveal-answer q=”752007″]Show Solution[/reveal-answer]
[hidden-answer a=”752007″]Write the formula for an inverse variation relationship.
\(y=\frac{k}{x}\)
Substitute known values into the equation.
\(25=\frac{k}{5}\)
Solve for k by multiplying both sides of the equation by 5.
\(\begin{array}{c}5\cdot 25=\frac{k}{5}\cdot 5\\\\125=\frac{5k}{5}\\\\125=k\,\,\,\end{array}\)
Answer
The constant of variation, k, is 125.
[/hidden-answer]
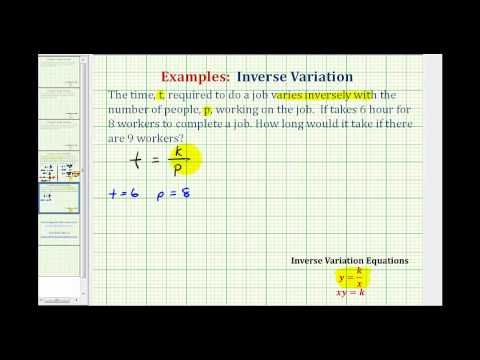
In the next example, we will find the water temperature in the ocean at a depth of 500 meters. Water temperature is inversely proportional to depth in the ocean.
Example
The water temperature in the ocean varies inversely with the depth of the water. The deeper a person dives, the colder the water becomes. At a depth of 1,000 meters, the water temperature is 5º Celsius. What is the water temperature at a depth of 500 meters?
[reveal-answer q=”700119″]Show Solution[/reveal-answer]
[hidden-answer a=”700119″]You are told that this is an inverse relationship, and that the water temperature (y) varies inversely with the depth of the water (x).
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=\frac{k}{x}\\\\temp=\frac{k}{depth}\end{array}\)
Substitute known values into the equation.
\(5=\frac{k}{1,000}\)
Solve for k.
\(\begin{array}{l}1,000\cdot5=\frac{k}{1,000}\cdot 1,000\\\\\,\,\,\,\,\,\,\,5,000=\frac{1,000k}{1,000}\\\\\,\,\,\,\,\,\,\,5,000=k\end{array}\)
Now that k, the constant of variation is known, use that information to solve the problem: find the water temperature at 500 meters.
\(\begin{array}{l}temp=\frac{k}{depth}\\\\temp=\frac{5,000}{500}\\\\temp=10\end{array}\)
Answer
At 500 meters, the water temperature is 10º C.
[/hidden-answer]
In the video that follows, we present an example of inverse variation.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
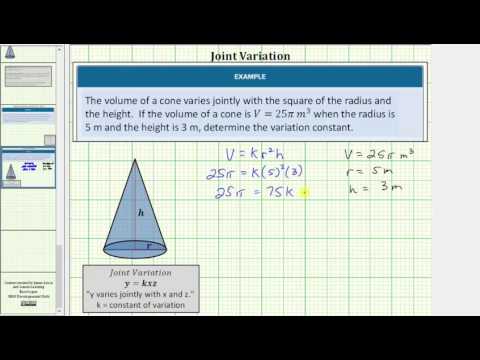
Joint Variation
A third type of variation is called joint variation. Joint variation is the same as direct variation except there are two or more quantities. For example, the area of a rectangle can be found using the formula \(A=lw\), where l is the length of the rectangle and w is the width of the rectangle. If you change the width of the rectangle, then the area changes and similarly if you change the length of the rectangle then the area will also change. You can say that the area of the rectangle “varies jointly with the length and the width of the rectangle.”
The formula for the volume of a cylinder, \(\pi\).
Example
The area of a triangle varies jointly with the lengths of its base and height. If the area of a triangle is 30 inches\(^{2}\) when the base is 10 inches and the height is 6 inches, find the variation constant and the area of a triangle whose base is 15 inches and height is 20 inches.
[reveal-answer q=”264626″]Show Solution[/reveal-answer]
[hidden-answer a=”264626″]You are told that this is a joint variation relationship, and that the area of a triangle (A) varies jointly with the lengths of the base (b) and height (h).
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=kxz\\Area=k(base)(height)\end{array}\)
Substitute known values into the equation, and solve for k.
\(30=k\left(10\right)\left(6\right)\\30=60k\\\\\frac{30}{60}=\frac{60k}{60}\\\\\frac{1}{2}=k\)
Now that k is known, solve for the area of a triangle whose base is 15 inches and height is 20 inches.
\(\begin{array}{l}Area=k(base)(height)\\\\Area=(15)(20)(\frac{1}{2})\\\\Area=\frac{300}{2}\\\\Area=150\,\,\text{square inches}\end{array}\)
Answer
The constant of variation, k, is \(\frac{1}{2}\), and the area of the triangle is 150 square inches.
[/hidden-answer]
Finding k to be \(A=\frac{1}{2}bh\). The \(\frac{1}{2}\) that you calculated in this example!
In the following video, we show an example of finding the constant of variation for a jointly varying relation.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132
Direct, Joint, and Inverse Variation
k is the constant of variation. In all cases, \(k\neq0\).
- Direct variation: \(y=kx\)
- Inverse variation: \(y=\frac{k}{x}\)
- Joint variation: \(y=kxz\)
Summary
Rational formulas can be used to solve a variety of problems that involve rates, times, and work. Direct, inverse, and joint variation equations are examples of rational formulas. In direct variation, the variables have a direct relationship—as one quantity increases, the other quantity will also increase. As one quantity decreases, the other quantity decreases. In inverse variation, the variables have an inverse relationship—as one variable increases, the other variable decreases, and vice versa. Joint variation is the same as direct variation except there are two or more variables.
Summary
You can solve rational equations by finding a common denominator. By rewriting the equation so that all terms have the common denominator, you can solve for the variable using just the numerators. Or, you can multiply both sides of the equation by the least common multiple of the denominators so that all terms become polynomials instead of rational expressions.
An important step in solving rational equations is to reject any extraneous solutions from the final answer. Extraneous solutions are solutions that don’t satisfy the original form of the equation because they produce untrue statements or are excluded values that make a denominator equal to 0.
- "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/. "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/. "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/. ↵
- Obialor, Ambrose, Churchill Ihentuge, and Frank Akapuaka. "Determination of Height Using Femur Length in Adult Population of Oguta Local Government Area of Imo State Nigeria." Federation of American Societies for Experimental Biology, April 2015. Accessed June 22, 2016. www.fasebj.org/content/29/1_Supplement/LB19.short. ↵
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Solve Basic Rational Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/R9y2D9VFw0I. License: CC BY: Attribution
- Solve Rational Equations with Like Denominators. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/gGA-dF_aQQQ. License: CC BY: Attribution
- Solve Basic Rational Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/R9y2D9VFw0I. License: CC BY: Attribution
- Screenshot: A Good Day's Work. Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: Matroyshka, or nesting dolls.. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: map with scale factor. Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Proportion Applications: Map Scale Factor (Clear Fractions, No Cross Products). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/id3sp4wvmVg. License: CC BY: Attribution
- Screenshot: so many cars, so many tires. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: Water temperature in the ocean varies inversely with depth. Provided by: Lumen Learning. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/JREPATMScbM. License: CC BY: Attribution
- Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. License: CC BY: Attribution
- Ex 2: Solve a Literal Equation for a Variable. Authored by: James Sousa (Mathispower4u.com). Located at: https://www.youtube.com/watch?v=ecEUUbRLDQs&feature=youtu.be. License: CC BY: Attribution
- Ex 1: Rational Equation Application - Painting Together. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/SzSasnDF7Ms. License: CC BY: Attribution
- Ex: Rational Equation App - Find Individual Working Time Given Time Working Together. Authored by: James Sousa (Mathispower4u.com) . Located at: https://www.youtube.com/watch?v=kbRSYb8UYqU&feature=youtu.be. License: CC BY: Attribution
- Ex: Proportion Applications - Mixtures . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/yGid1a_x38g. License: CC BY: Attribution
- Ex: Direct Variation Application - Aluminum Can Usage. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/DLPKiMD_ZZw. License: CC BY: Attribution
- Ex: Inverse Variation Application - Number of Workers and Job Time. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/y9wqI6Uo6_M. License: CC BY: Attribution