8.2: Identify and Simplify Roots

Last updated

Sep 27, 2020
Save as PDF
- 8.1: Why It Matters- Roots and Rational Exponents
- 8.3: Operations on Radical Expressions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Square Roots
- Use square root notation to write principal square roots
- Simplify principal square roots using factorization
Cube Roots
- Use cube root notation to write cube roots
- Simplify cube roots using factorization
Simplify Square Roots
- Simplify square roots with variables
- Determine when a simplified root needs an absolute value
Rational Exponents
- Convert between radical and exponent notation
- Use the laws of exponents to simplify expressions with rational exponents
- Use rational exponents to simplify radical expressions

We know how to square a number:

$\left(-5\right)^2=25$

Taking a square root is the opposite of squaring so we can make these statements:

5 is the nonngeative square root of 25
-5 is the negative square root of 25

Find the square roots of the following numbers:

We want to find a number whose square is 36. $6^2=36$ therefore, the nonnegative square root of 36 is 6 and the negative square root of 36 is -6
We want to find a number whose square is 81. $9^2=81$ therefore, the nonnegative square root of 81 is 9 and the negative square root of 81 is -9
We want to find a number whose square is -49. When you square a real number, the result is always positive. Stop and think about that for a second. A negative number times itself is positive, and a positive number times itself is positive. Therefore, -49 does not have square roots, there are no real number solutions to this question.
We want to find a number whose square is 0. $0^2=0$ therefore, the nonnegative square root of 0 is 0. We do not assign 0 a sign, so it has only one square root, and that is 0.

The notation that we use to express a square root for any real number, a, is as follows:

Writing a Square Root

The symbol for the square root is called a radical symbol. For a real number, a the square root of a is written as $\sqrt{a}$

The number that is written under the radical symbol is called the radicand.

By definition, the square root symbol, $\sqrt{\hphantom{5}}$ always means to find the nonnegative root, called the principal root.

$\sqrt{a}$ is defined for $a>0$

Let’s do an example similar to the example from above, this time using square root notation. Note that using the square root notation means that you are only finding the principal root – the nonnegative root.

Example

Simplify the following square roots:

$\sqrt{16}$
$\sqrt{9}$
$\sqrt{-9}$
$\sqrt{5^2}$

[reveal-answer q=”614386″]Show Solution[/reveal-answer]
[hidden-answer a=”614386″]

$\sqrt{16}=4$ . We only write the nonnegative root because that is how the root symbol is defined.
$\sqrt{9}=3$ . We only write the nonnegative root because that is how the root symbol is defined.
$\sqrt{-9}$ . We are looking for a number whose square is -9. There are no real numbers whose square is -9, so this radical is not a real number.
$5^2$ . We already have the number whose square is $5^2$ , it’s 5!

[/hidden-answer]

The last problem in the previous example shows us an important relationship between squares and square roots, and we can summarize it as follows:

The square root of a square

For a nonnegative real number, a, $\sqrt{a^2}=a$

In the video that follows, we simplify more square roots using the fact that $\sqrt{a^2}=a$ means finding the principal square root.

$Thumbnail for the embedded element "Simplify Square Roots (Perfect Square Radicands)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

What if you are working with a number whose square you do not know right away? We can use factoring and the product rule for square roots to find square roots such as $\sqrt{225}$ .

The Product Rule for Square Roots

Given that a and b are nonnegative real numbers, $\sqrt{a\cdot{b}}=\sqrt{a}\cdot\sqrt{b}$

In the examples that follow we will bring together these ideas to simplify square roots of numbers that are not obvious at first glance:

square root of a square,
the product rule for square roots
factoring

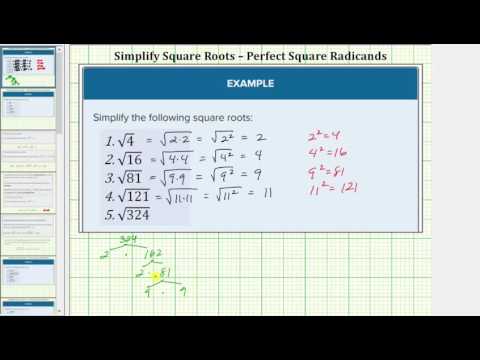
Example

Simplify $\sqrt{144}$

[reveal-answer q=”620082″]Show Solution[/reveal-answer]
[hidden-answer a=”620082″]

Determine the prime factors of 144.

$\begin{array}{c}\sqrt{144}\\\\\sqrt{2\cdot 72}\\\\\sqrt{2\cdot 2\cdot 36}\\\\\sqrt{2\cdot 2\cdot 2\cdot 18}\\\\\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 9}\\\\\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3}\end{array}$

Because we are finding a square root, we regroup these factors into squares.

$\sqrt{2^2\cdot 2^2\cdot3^2}$

Now we can use the product rule for square roots and the square root of a square idea to finish finding the square root.

$\begin{array}{c}\sqrt{2^2\cdot 2^2\cdot3^2}\\\\=\sqrt{2^2}\cdot\sqrt{2^2}\cdot\sqrt{3^2}\\\\=2\cdot3\cdot2\\\\=12\end{array}$

Answer

$\sqrt{144}=12$

[/hidden-answer]

Example

Simplify $\sqrt{225}$
[reveal-answer q=”686109″]Show Solution[/reveal-answer]
[hidden-answer a=”686109″]

First, factor 225:

$\begin{array}{c}\sqrt{225}\\\\=\sqrt{5\cdot45}\\\\=\sqrt{5\cdot5\cdot9}\\\\=\sqrt{5\cdot5\cdot3\cdot3}\end{array}$

Because we are finding a square root, we regroup these factors into squares. Finish simplifying with the product rule for roots, and the square of a square idea.

$\begin{array}{c}\sqrt{5^2\cdot3^2}\\\\=\sqrt{5^2}\cdot\sqrt{3^2}\\\\=5\cdot3=15\end{array}$

Answer

$\sqrt{225}=15$

[/hidden-answer]

$Caution$ Caution! The square root of a product rule applies when you have multiplication ONLY under the square root. You cannot apply the rule to sums:

$\sqrt{a+b}\ne\sqrt{a}+\sqrt{b}$

Prove this to yourself with some real numbers: let a = 64 and b = 36, then use the order of operations to simplify each expression.

$\begin{array}{c}\sqrt{64+36}=\sqrt{100}=10\\\\\sqrt{64}+\sqrt{36}=8+6=14\\\\10\ne14\end{array}$

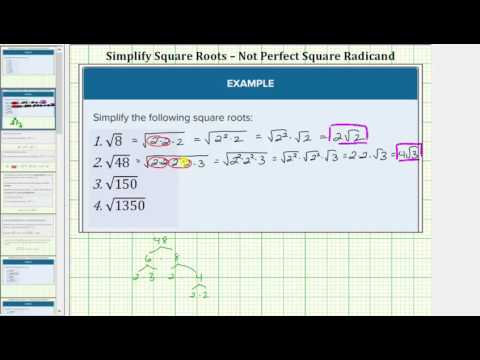
So far, you have seen examples that are perfect squares. That is, each is a number whose square root is an integer. But many radical expressions are not perfect squares. Some of these radicals can still be simplified by finding perfect square factors. The example below illustrates how to factor the radicand, looking for pairs of factors that can be expressed as a square.

Example

Simplify. $\sqrt{63}$

[reveal-answer q=”908978″]Show Solution[/reveal-answer]
[hidden-answer a=”908978″]Factor 63

$\sqrt{7\cdot 3\cdot3}$

Regroup factors into squares

$\sqrt{7\cdot3^2}$

Finish simplifying with the product rule for roots, and the square of a square idea.

$\sqrt{7\cdot3^2}\\\\=\sqrt{7}\cdot\sqrt{3^2}\\\\=\sqrt{7}\cdot3$

Since 7 is prime and we can’t write it as a square, it will have to stay under the radical sign. As a matter of convention, we write the constant, 3, in front of the radical. This helps the reader know that the 3 is not under the radical anymore.

$3\cdot \sqrt{7}$

Answer

$\sqrt{63}=3\sqrt{7}$

[/hidden-answer]

The final answer $3\sqrt{7}$ may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”

$Picture of a sidewalk leading to a parking lot. There is a path through the grass to teh right of the sidewalk through the trees that has been made by people walking on the grass. The shortcut to the parking lot is the preferred way.$

Shortcut This Way

In the next example, we take a bit of a shortcut by making use of the common squares we know, instead of using prime factors. It helps to have the squares of the numbers between 0 and 10 fresh in your mind to make simplifying radicals faster.

$0^2=0$
$2^2=4$
$3^2=9$
$4^2=16$
$5^2=25$
$6^2=36$
$7^2=49$
$8^2=64$
$9^2=81$
$10^2=100$

Example

Simplify. $\sqrt{2,000}$

[reveal-answer q=”932245″]Show Solution[/reveal-answer]
[hidden-answer a=”932245″]Factor 2,000 to find perfect squares.

$\begin{array}{r}\sqrt{100\cdot 20}\\\\=\sqrt{100\cdot 4\cdot 5}\end{array}$

$100=10^2,4=2^2$

$\begin{array}\sqrt{100\cdot 4\cdot 5}\\\\= \sqrt{10^2\cdot 4^2\cdot 5}\\\\=\sqrt{10^2}\cdot\sqrt{4^2}\cdot\sqrt{5}\\\\=10\cdot4\cdot\sqrt{5}$

Multiply.

$20\cdot \sqrt{5}$

Answer

$\sqrt{2,000}=20\sqrt{5}$

[/hidden-answer]

In this last video, we show examples of simplifying radicals that are not perfect squares.

$Thumbnail for the embedded element "Simplify Square Roots (Not Perfect Square Radicands)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

Cube Roots

$Rubik's cube$

Rubik’s Cune

While square roots are probably the most common radical, you can also find the third root, the fifth root, the 10th root, or really any other nth root of a number. Just as the square root is a number that, when squared, gives the radicand, the cube root is a number that, when cubed, gives the radicand.

Find the cube roots of the following numbers:

27
8
-8
0

We want to find a number whose cube is 27. $9=3^2$ , so $3/cdot3/cdot3=3^3=27$
We want to find a number whose cube is 8. $2\cdot2\cdot2=8$ the cube root of 8 is 2.
We want to find a number whose cube is -8. We know 2 is the cube root of 8, so maybe we can try -2. $-2\cdot{-2}\cdot{-2}=-8$ , so the cube root of -8 is -2. This is different from square roots because multiplying three negative numbers together results in a negative number.
We want to find a number whose cube is 0. $0$ by itself, you will always get $0$ .

The cube root of a number is written with a small number 3, called the index, just outside and above the radical symbol. It looks like $\sqrt[3]$ . This little 3 distinguishes cube roots from square roots which are written without a small number outside and above the radical symbol.

$3\sqrt{x}$ , three times the square root of x. They may look similar at first, but they lead you to much different expressions!

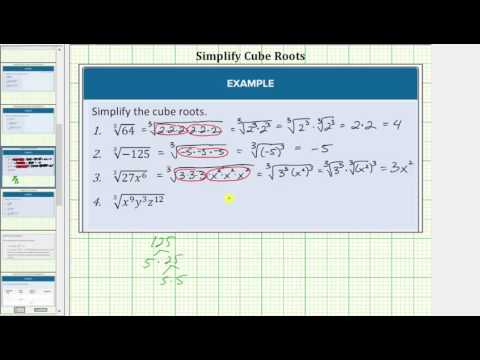
We can also use factoring to simplify cube roots such as $\sqrt[3]{125}$ . You can read this as “the third root of 125” or “the cube root of 125.” To simplify this expression, look for a number that, when multiplied by itself two times (for a total of three identical factors), equals 125. Let’s factor 125 and find that number.

Example

Simplify. $\sqrt[3]{125}$

[reveal-answer q=”517592″]Show Solution[/reveal-answer]
[hidden-answer a=”517592″]125 ends in 5, so you know that 5 is a factor. Expand 125 into $5\cdot25$ .

$\sqrt[3]{5\cdot 25}$

Factor 25 into 5 and 5.

$\sqrt[3]{5\cdot 5\cdot 5}$

The factors are $5^{3}$ .

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[3]/p[7]/span, line 1, column 3

Answer

$\sqrt[3]{125}=5$

[/hidden-answer]

The prime factors of 125 are $5^{3}$ . The cube root of a cubed number is the number itself, so \(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[3]/div/p[3]/span, line 1, column 3

=5\). You have found the cube root, the three identical factors that when multiplied together give 125. 125 is known as a perfect cube because its cube root is an integer.

Here’s an example of how to simplify a radical that is not a perfect cube.

Example

Simplify. \(\sqrt[3]{32

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[1]/span, line 1, column 2

}\)

[reveal-answer q=”617053″]Show Solution[/reveal-answer]
[hidden-answer a=”617053″]Factor 32 into prime factors.

\(\sqrt[3]{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[3]/span, line 1, column 2

}\)

Since you are looking for the cube root, you need to find factors that appear 3 times under the radical. Rewrite \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[4]/span, line 1, column 2

\).

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[5]/span, line 1, column 3

Rewrite \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[6]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[6]/span[2], line 1, column 2

\).

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[7]/span, line 1, column 3

Rewrite the expression as a product of multiple radicals.

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[9]/span[1], line 1, column 3

\cdot \sqrt[3]{2\cdot 2}\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[9]/span[2], line 1, column 3

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[9]/span[3], line 1, column 3

Simplify and multiply.

\(2\cdot \sqrt[3]{4}\cdot m\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/p[11]/span, line 1, column 3

Answer

\(\sqrt[3]{32

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/div/p[1]/span[1], line 1, column 2

}=2m\sqrt[3]{4

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/div/p[1]/span[2], line 1, column 2

}\)

[/hidden-answer]

In the example below, we use the following idea:

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[4]/div/p[4]/span, line 1, column 6

=-1\)

to simplify the radical. You do not have to do this, but it may help you recognize cubes more easily when they are nonnegative.

Example

Simplify. \(\sqrt[3]{-27

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[1]/span[2], line 1, column 2

}\)

[reveal-answer q=”670300″]Show Solution[/reveal-answer]
[hidden-answer a=”670300″]Factor the expression into cubes.

Separate the cubed factors into individual radicals.

\(\begin{array}{r}\sqrt[3]{-1\cdot 27\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[2], line 1, column 2

}\\\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[3], line 1, column 6

\\\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[4], line 1, column 6

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[5], line 1, column 5

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[6], line 1, column 3

\cdot \sqrt[3]{x}\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/p[4]/span[7], line 1, column 3

\end{array}\)

Simplify the cube roots.

$-1\cdot 3\cdot x\cdot y\cdot \sqrt[3]{x}$

Answer

\(\sqrt[3]{-27

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[1]/span[2], line 1, column 2

}=-3xy\sqrt[3]{x}\)

[/hidden-answer]

In the video that follows, we show more examples if simplifying cube roots.

$Thumbnail for the embedded element "Simplify Cube Roots (Perfect Cube Radicands)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

You could check your answer by performing the inverse operation. If you are right, when you cube \(-27

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[4]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[4]/span[2], line 1, column 2

\).

\(\begin{array}{l}\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right)\left( -3xy\sqrt[3]{x} \right)\\-3\cdot -3\cdot -3\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\cdot \sqrt[3]{x}\\-27\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[2], line 1, column 2

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[3], line 1, column 3

\\-27

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[4], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[5], line 1, column 2

\cdot x\\-27

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[6], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[5]/div/p[5]/span[7], line 1, column 2

\end{array}\)

You can find the odd root of a negative number, but you cannot find the even root of a negative number. This means you can simplify the radicals $\sqrt[7]{-2187}$ , but you cannot simplify the radicals $\sqrt[6]{-2,500}$ .

Let’s look at another example.

Example

Simplify. \(\sqrt[3]{-24

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[1]/span, line 1, column 2

}\)

[reveal-answer q=”473861″]Show Solution[/reveal-answer]
[hidden-answer a=”473861″]Factor $−1$ and 8 are the perfect cubes.

\(\sqrt[3]{-1\cdot 8\cdot 3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[3]/span, line 1, column 2

}\)

Factor variables. You are looking for cube exponents, so you factor $a^{3}$ and $a^{2}$ .

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[5]/span, line 1, column 6

Separate the factors into individual radicals.

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[7]/span[1], line 1, column 6

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[7]/span[2], line 1, column 3

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[7]/span[3], line 1, column 3

\cdot \sqrt[3]{3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[7]/span[4], line 1, column 2

}\)

Simplify, using the property \(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[8]/span, line 1, column 3

=x\).

\(-1\cdot 2\cdot a\cdot \sqrt[3]{3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[9]/span, line 1, column 2

}\)

This is the simplest form of this expression; all cubes have been pulled out of the radical expression.

\(-2a\sqrt[3]{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/p[11]/span, line 1, column 2

}\)

Answer

\(\sqrt[3]{-24

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[1]/p[1]/span[1], line 1, column 2

}=-2a\sqrt[3]{3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[1]/p[1]/span[2], line 1, column 2

}\)

[/hidden-answer]

The steps to consider when simplifying a radical are outlined below.

Simplifying a radical

When working with exponents and radicals:

If n is odd, \(\sqrt[n]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[1]/div/div/ul/li[1]/span, line 1, column 3

=x\).

If n is even, $\sqrt[n]
ParseError: colon expected (click for details)
```
Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[1]/div/div/ul/li[2]/span, line 1, column 3
```
=\left| x \right|$. (The absolute value accounts for the fact that if x is negative and raised to an even power, that number will be positive, as will the nth principal root of that number.)

Example

Simplify. \(\sqrt{100

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[1]/span[2], line 1, column 2

}\)

[reveal-answer q=”982628″]Show Solution[/reveal-answer]
[hidden-answer a=”982628″]Separate factors; look for squared numbers and variables. Factor 100 into $10\cdot10$ .

\(\sqrt{10\cdot 10\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[3]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[3]/span[2], line 1, column 2

}\)

Factor $\left(y^{2}\right)^{2}$ .

\(\sqrt{10\cdot 10\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[5]/span[1], line 1, column 2

\cdot

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[5]/span[2], line 1, column 3

}\)

Separate the squared factors into individual radicals.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[7]/span[1], line 1, column 4

\cdot \sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[7]/span[2], line 1, column 3

\cdot \sqrt

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/p[7]/span[3], line 1, column 4

Take the square root of each radical . Since you do not know whether x is positive or negative, use $\left|x\right|$ to account for both possibilities, thereby guaranteeing that your answer will be positive.

$10\cdot\left|x\right|\cdot{y}^{2}$

Simplify and multiply.

$10\left|x\right|y^{2}$

Answer

\(\sqrt{100

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/div/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/div/p[1]/span[2], line 1, column 2

}=10\left| x \right|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/div/p[1]/span[3], line 1, column 2

[/hidden-answer]

You can check your answer by squaring it to be sure it equals \(100

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/div/p[3]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[10]/div[6]/div[2]/div/p[3]/span[2], line 1, column 2

\).

In the last video, we share examples of finding cube roots with negative radicands.

$Thumbnail for the embedded element "Simplify Cube Roots (Not Perfect Cube Radicands)"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

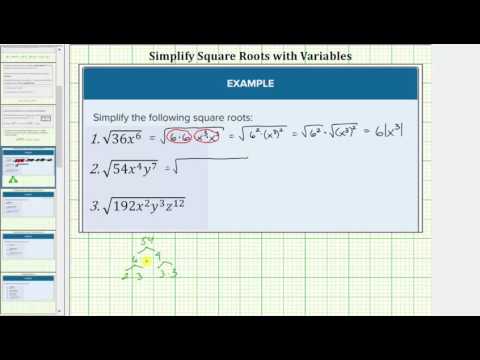
Simplify Square Roots with Variables

Radical expressions are expressions that contain radicals. Radical expressions come in many forms, from simple and familiar, such as\(\sqrt[3]{250

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[11]/p/span, line 1, column 2

y}\). Using factoring, you can simplify these radical expressions, too.

$Radical: of or going to the root or origin; fundamental: a radical difference$

Radical

Simplifying Square Roots

Radical expressions will sometimes include variables as well as numbers. Consider the expression \(\sqrt{9

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/p[1]/span, line 1, column 2

}\). Simplifying a radical expression with variables is not as straightforward as the examples we have already shown with integers.

Consider the expression \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/p[2]/span, line 1, column 3

\). This looks like it should be equal to x, right? Let’s test some values for x and see what happens.

In the chart below, look along each row and determine whether the value of x is the same as the value of \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/p[3]/span, line 1, column 3

\). Where are they equal? Where are they not equal?

After doing that for each row, look again and determine whether the value of $\left|x\right|$ .

$x^{2}$	$\left\|x\right\|$
$−2$	4	2	2
0	0	0	0
6	36	6	6
10	100	10	10

Notice—in cases where x is a negative number, $\sqrt{x^{2}}=\left|x\right|$ . You need to consider this fact when simplifying radicals that contain variables, because by definition $\sqrt{x^{2}}$ is always nonnegative.

Taking the Square Root of a Radical Expression

When finding the square root of an expression that contains variables raised to a power, consider that $\sqrt{x^{2}}=\left|x\right|$ .

Examples: \(\sqrt{16

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[1]/div/p[2]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[1]/div/p[2]/span[2], line 1, column 2

}=4\left|xy\right|\)

Let’s try it.
The goal is to find factors under the radical that are perfect squares so that you can take their square root.

Example

Simplify. \(\sqrt{9

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[1]/span, line 1, column 2

}\)

[reveal-answer q=”41297″]Show Solution[/reveal-answer]
[hidden-answer a=”41297″]Factor to find identical pairs.

\(\sqrt{3\cdot 3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[3]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[3]/span[2], line 1, column 2

}\)

Rewrite the pairs as perfect squares, note how we use the power rule for exponents to simplify ${x^3}^2$

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[5]/span, line 1, column 3

Separate into individual radicals.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[7]/span[1], line 1, column 3

\cdot \sqrt

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[7]/span[2], line 1, column 2

Simplify, using the rule that \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[8]/span, line 1, column 3

=\left|x\right|\).

\(3\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/p[9]/span, line 1, column 2

\right|\)

Answer

\(\sqrt{9

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[1]/span[1], line 1, column 2

}=3\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[1]/span[2], line 1, column 2

\right|\)

[/hidden-answer]

Variable factors with even exponents can be written as squares. In the example above, \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[3]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[3]/span[2], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[3]/span[3], line 1, column 2

={\left|x^3\right|}^{2}\) and

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[4]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[4]/span[2], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[2]/div/p[4]/span[3], line 1, column 2

={\left(|y^2\right|)}^{2}\).

Let’s try to simplify another radical expression.

Example

Simplify. \(\sqrt{49

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[1]/span[2], line 1, column 2

}\)

[reveal-answer q=”283065″]Show Solution[/reveal-answer]
[hidden-answer a=”283065″]Look for squared numbers and variables. Factor 49 into $x^{10}$ into $y^{8}$ into $y^{4}\cdot{y}^{4}$ .

\(\sqrt{7\cdot 7\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[3]/span[1], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[3]/span[2], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[3]/span[3], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[3]/span[4], line 1, column 2

}\)

Rewrite the pairs as squares.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[5]/span, line 1, column 3

Separate the squared factors into individual radicals.

$\sqrt{7^2}\cdot\sqrt{({x^5})^2}\cdot\sqrt{({y^4})^2}$

Take the square root of each radical using the rule that \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[8]/span, line 1, column 3

=\left|x\right|\).

\(7\cdot\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[9]/span[1], line 1, column 2

\right|\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[9]/span[2], line 1, column 2

Multiply.

\(7\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[11]/span[1], line 1, column 2

\right|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/p[11]/span[2], line 1, column 2

Answer

\(\sqrt{49

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[1]/span[2], line 1, column 2

}=7\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[1]/span[3], line 1, column 2

\right|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[1]/span[4], line 1, column 2

[/hidden-answer]

You find that the square root of \(7\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[1], line 1, column 2

\right|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[2], line 1, column 2

\). In order to check this calculation, you could square \(49

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[3], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[4], line 1, column 2

\). And, in fact, you would get this expression if you evaluated \({\left({7\left|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[5], line 1, column 2

\right|

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[3]/div/p[3]/span[6], line 1, column 2

}\right)^{2}}\).

In the video that follows we show several examples of simplifying radicals with variables.

$Thumbnail for the embedded element "Simplify Square Roots with Variables"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

Example

Simplify. \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[1]/span, line 1, column 3

[reveal-answer q=”141094″]Show Solution[/reveal-answer]
[hidden-answer a=”141094″]Factor to find variables with even exponents.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[3]/span, line 1, column 3

Rewrite $\left(b^{2}\right)^{2}$ .

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[5]/span, line 1, column 3

Separate the squared factors into individual radicals.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[7]/span[1], line 1, column 3

\cdot\sqrt

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[7]/span[2], line 1, column 4

\cdot\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[7]/span[3], line 1, column 3

\cdot \sqrt{a\cdot b}\)

Take the square root of each radical. Remember that \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[8]/span, line 1, column 3

=\left| a \right|\).

\(\left| a \right|\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[9]/span, line 1, column 2

\cdot\left|{c}\right|\cdot\sqrt{a\cdot b}\)

Simplify and multiply. The entire quantity $b^2$ will be positive anyway.

\(\left| a

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/p[11]/span, line 1, column 2

c \right|\sqrt{ab}\)

Answer

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/div/p[1]/span[1], line 1, column 3

=\left| a

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[12]/div[4]/div/p[1]/span[2], line 1, column 2

c\right|\sqrt{ab}\)

[/hidden-answer]

In the next section, we will explore cube roots, and use the methods we have shown here to simplify them. Cube roots are unique from square roots in that it is possible to have a negative number under the root, such as $\sqrt[3]{-125}$ .

Rational Exponents

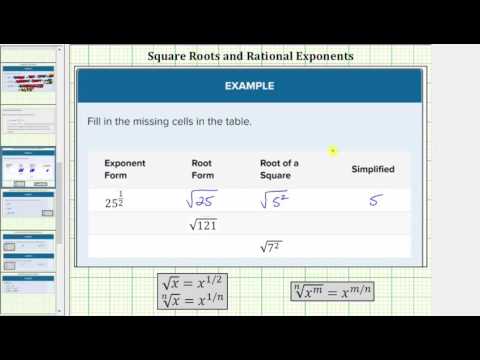
Roots can also be expressed as fractional exponents. The square root of a number can be written with a radical symbol or by raising the number to the $\frac{1}{2}$ power. This is illustrated in the table below.

Exponent Form	Root Form	Root of a Square	Simplified
$\sqrt{25}$	\( ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[1]/td[2]/span, line 1, column 3 \)	\(\sqrt ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[1]/td[3]/span, line 1, column 3 \)	4
$\sqrt{100}$	\(\sqrt ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[2]/td[2]/span, line 1, column 4 \)	10

Exponent Form

Root Form

Root of a Square

Simplified

$\sqrt{25}$

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[1]/td[2]/span, line 1, column 3

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[1]/td[3]/span, line 1, column 3

$\sqrt{100}$

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[1]/tbody/tr[2]/td[2]/span, line 1, column 4

Use the example below to familiarize yourself with the different ways to write square roots.

Example

Fill in the missing cells in the table.

Exponent Form

Root Form

Root of a Square

Simplified

$\sqrt{81}$

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[1]/tbody/tr[2]/td[3]/span, line 1, column 4

[reveal-answer q=”990781″]Show Solution[/reveal-answer]
[hidden-answer a=”990781″]

Exponent Form	Root Form	Root of a Square	Simplified
$\sqrt{36}$	\( ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[1]/td[2]/span, line 1, column 3 \)	\(\sqrt ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[1]/td[3]/span, line 1, column 3 \)	9
$\sqrt{144}$	\(\sqrt ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[2]/td[2]/span, line 1, column 4 \)	12

Exponent Form

Root Form

Root of a Square

Simplified

$\sqrt{36}$

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[1]/td[2]/span, line 1, column 3

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[1]/td[3]/span, line 1, column 3

$\sqrt{144}$

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/div[1]/table[2]/tbody/tr[2]/td[2]/span, line 1, column 4

[/hidden-answer]

In the following video, we show another example of filling in a table to connect the different notation used for roots.

$Thumbnail for the embedded element "Write Basic Expression in Radical Form and Using Rational Exponents"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

We can extend the concept of writing $\sqrt{x}=x^{\frac{1}{2}}$ to cube roots. Remember, cubing a number raises it to the power of three. Notice that in these examples, the denominator of the rational exponent is the number 3.

Radical Form	Exponent Form	Integer
\( ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[1]/td[1]/span, line 1, column 2 \)	2
\( ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[2]/td[1]/span, line 1, column 4 \)	5
\( ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[3]/td[1]/span, line 1, column 5 \)	10

Radical Form

Exponent Form

Integer

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[1]/td[1]/span, line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[2]/td[1]/span, line 1, column 4

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[2]/tbody/tr[3]/td[1]/span, line 1, column 5

These examples help us model a relationship between radicals and rational exponents: namely, that the nth root of a number can be written as either \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/p[5]/span, line 1, column 2

\).

Radical Form	Exponent Form
$ ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[3]/tbody/tr[1]/td/span, line 1, column 2 $
$ ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[3]/tbody/tr[2]/td/span, line 1, column 2 $
$ ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[3]/tbody/tr[3]/td/span, line 1, column 2 $
…	…
$ ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[13]/table[3]/tbody/tr[5]/td/span, line 1, column 2 $

Convert Between Radical and Exponent Notation

When faced with an expression containing a rational exponent, you can rewrite it using a radical. In the table above, notice how the denominator of the rational exponent determines the index of the root. So, an exponent of $\frac{1}{5}$ translates to the fifth root or $\frac{1}{8}$ translates to the eighth root or \(\sqrt[8]

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/p/span, line 1, column 1

\) .

Example

Write $\sqrt[4]$ can be rewritten as the exponent $\frac{1}{4}$ . Remove the radical and place the exponent next to the base.

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[1]/p[2]/span, line 1, column 3

Answer

\(\sqrt[3]{81}=

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[1]/div/p[1]/span, line 1, column 3

[/hidden-answer]

Example

Express \(

ParseError: ")" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[2]/p[1]/span, line 1, column 3

\) in radical form.

[reveal-answer q=”581351″]Show Solution[/reveal-answer]
[hidden-answer a=”581351″]Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

$\sqrt[3]{2x}$

The parentheses in \(

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[2]/p[4]/span, line 1, column 1

\) indicate that the exponent refers to everything within the parentheses.

Answer

ParseError: ")" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[2]/div/p[1]/span, line 1, column 3

=\sqrt[3]{2x}\)

[/hidden-answer]

Remember that exponents only refer to the quantity immediately to their left unless a grouping symbol is used. The example below looks very similar to the previous example with one important difference—there are no parentheses! Look what happens.

Example

Express \(2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[3]/p[1]/span, line 1, column 2

\) in radical form.

[reveal-answer q=”236347″]Show Solution[/reveal-answer]
[hidden-answer a=”236347″]Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

$2\sqrt{x}$

The exponent refers only to the part of the expression immediately to the left of the exponent, in this case x, but not the 2.

Answer

\(2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[3]/div/p[1]/span, line 1, column 2

=2\sqrt{x}\)

[/hidden-answer]

The next example is intended to help you practice placing a rational exponent on the appropriate terms in an expression that is written in radical form

Example

Express $4\sqrt[3]{xy}$ with rational exponents.

[reveal-answer q=”527560″]Show Solution[/reveal-answer]
[hidden-answer a=”527560″]Rewrite the radical using a rational exponent. The root determines the fraction. In this case, the index of the radical is 3, so the rational exponent will be $\frac{1}{3}$ .

\(4

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[4]/p[3]/span, line 1, column 5

Since 4 is outside the radical, it is not included in the grouping symbol and the exponent does not refer to it.

Answer

\(4\sqrt[3]{xy}=4

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[14]/div[4]/div/p[1]/span, line 1, column 5

[/hidden-answer]

In the next video, we show examples of converting between radical and exponent form.

$Thumbnail for the embedded element "Write Expressions Using Radicals and Rational Exponents"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

When converting from radical to rational exponent notation, the degree of the root becomes the denominator of the exponent. If you start with a square root, you will have an exponent of $\frac{1}{3}$ you will use a cube root. The following statement summarizes this idea.

Writing Fractional Exponents

Any radical in the form $a^{\frac{1}{n}}$ .

Simplifying Radical Expressions Using Rational Exponents and the Laws of Exponents

Let’s explore some radical expressions now and see how to simplify them. Let’s start by simplifying this expression, \(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/p[1]/span, line 1, column 3

\).

One method of simplifying this expression is to factor and pull out groups of $a^{3}$ , as shown below in this example.

Example

Simplify. \(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/p[1]/span, line 1, column 3

[reveal-answer q=”235013″]Show Solution[/reveal-answer]
[hidden-answer a=”235013″]Rewrite by factoring out cubes.

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/p[3]/span, line 1, column 3

Write each factor under its own radical and simplify.

\(\begin{array}{r}\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/p[5]/span[1], line 1, column 3

\cdot \sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/p[5]/span[2], line 1, column 3

\\a\cdot{a}\end{array}\)

Answer

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/div/p[1]/span[1], line 1, column 3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/div/p[1]/span[2], line 1, column 2

[/hidden-answer]

You can also simplify this expression by thinking about the radical as an expression with a rational exponent, and using the principle that any radical in the form \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[1]/div/p[3]/span, line 1, column 2

\).

Example

Simplify. \(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[2]/p[1]/span, line 1, column 3

[reveal-answer q=”898415″]Show Solution[/reveal-answer]
[hidden-answer a=”898415″]Rewrite the radical using a rational exponent.

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[2]/p[3]/span, line 1, column 2

Simplify the exponent.

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[2]/p[5]/span, line 1, column 2

Answer

\(\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[2]/div/p[1]/span[1], line 1, column 3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[2]/div/p[1]/span[2], line 1, column 2

[/hidden-answer]

Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.

Both simplification methods gave the same result, $a^{2}$ . Depending on the context of the problem, it may be easier to use one method or the other, but for now, you’ll note that you were able to simplify this expression more quickly using rational exponents than when using the “pull-out” method.

Let’s try another example.

Example

Simplify. \(\sqrt[4]{81

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[1]/span[2], line 1, column 2

}\)

[reveal-answer q=”324337″]Show Solution[/reveal-answer]
[hidden-answer a=”324337″]Rewrite the radical using rational exponents.

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[3]/span, line 1, column 5

Use the rules of exponents to simplify the expression.

\(\begin{array}{r}

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[1], line 1, column 3

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[2], line 1, column 2

\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[3], line 1, column 2

ParseError: ")" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[4], line 1, column 3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[5], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[6], line 1, column 2

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[7], line 1, column 3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[8], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[9], line 1, column 2

\\3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[10], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[5]/span[11], line 1, column 2

\end{array}\)

Change the expression with the rational exponent back to radical form.

\(3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[7]/span[1], line 1, column 2

\sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/p[7]/span[2], line 1, column 3

Answer

\(\sqrt[4]{81

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/div/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/div/p[1]/span[2], line 1, column 2

}=3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/div/p[1]/span[3], line 1, column 2

\sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[3]/div/p[1]/span[4], line 1, column 3

[/hidden-answer]

Again, the alternative method is to work on simplifying under the radical by using factoring. For the example you just solved, it looks like this.

Example

Simplify. \(\sqrt[4]{81

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[1]/span[1], line 1, column 2

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[1]/span[2], line 1, column 2

}\)

[reveal-answer q=”295348″]Show Solution[/reveal-answer]
[hidden-answer a=”295348″]Rewrite the expression.

\(\sqrt[4]{81}\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[3]/span[1], line 1, column 3

\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[3]/span[2], line 1, column 3

Factor each radicand.

\(\sqrt[4]{3\cdot 3\cdot 3\cdot 3}\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[5]/span[1], line 1, column 3

\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[5]/span[2], line 1, column 3

Simplify.

\(\begin{array}{r}\sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[7]/span[1], line 1, column 3

\cdot \sqrt[4]

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[7]/span[2], line 1, column 4

\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[7]/span[3], line 1, column 3

\\3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[7]/span[4], line 1, column 2

\cdot \sqrt[4]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[15]/div[4]/p[7]/span[5], line 1, column 3

\end{array}\)

Answer

$\sqrt[4]{81x^{8}y^{3}}=3x^{2}\sqrt[4]{y^{3}}$

[/hidden-answer]

The following video shows more examples of how to simplify a radical expression using rational exponents.

$Thumbnail for the embedded element "Simplify Radicals Using Rational Exponents"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=140

Summary

The square root of a number is the number which, when multiplied by itself, gives the original number. Principal square roots are always positive and the square root of 0 is 0. You can only take the square root of values that are nonnegative. The square root of a perfect square will be an integer. Other square roots can be simplified by identifying factors that are perfect squares and taking their square root.

A radical expression is a mathematical way of representing the nth root of a number. Square roots and cube roots are the most common radicals, but a root can be any number. To simplify radical expressions, look for exponential factors within the radical, and then use the property \(\sqrt[n]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[16]/p[2]/span, line 1, column 3

=\left| x \right|\) if n is even to pull out quantities. All rules of integer operations and exponents apply when simplifying radical expressions.

A radical can be expressed as an expression with a fractional exponent by following the convention \(\sqrt[n]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[16]/p[3]/span[1], line 1, column 3

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.02:_Identify_and_Simplify_Roots), /content/body/div[16]/p[3]/span[2], line 1, column 2

\). Rewriting radicals using fractional exponents can be useful in simplifying some radical expressions. When working with fractional exponents, remember that fractional exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.

Image: Shortcut this way.. Provided by: Lumen Learning. License: CC BY: Attribution
Simplify Square Roots (Perfect Square Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/B3riJsl7uZM. License: CC BY: Attribution
Simplify Square Roots (Not Perfect Square Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/oRd7aBCsmfU. License: CC BY: Attribution
Screenshot: Rubik's Cube. Provided by: Lumen Learning. License: CC BY: Attribution
Screenshot: Caution. Provided by: Lumen Learning. License: CC BY: Attribution
Simplify Cube Roots (Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/9Nh-Ggd2VJo. License: CC BY: Attribution
Simplify Cube Roots (Not Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: Simplify%20Cube%20Roots%20(Not%20Perfect%20Cube%20Radicands). License: CC BY: Attribution
Screenshot: radical. Provided by: Lumen Learning. License: CC BY: Attribution
Simplify Square Roots with Variables. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/q7LqsKPoAKo. License: CC BY: Attribution
Write Basic Expression in Radical Form and Using Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/eGJgmo2CpN4. License: CC BY: Attribution
Write Expressions Using Radicals and Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/5cWkVrANBWA. License: CC BY: Attribution
Simplify Radicals Using Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/CfxhFRHUq_M. License: CC BY: Attribution

Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution

Search

Text Color

Text Size

Margin Size

Font Type

Answer

Answer

Answer

Answer

Answer

Simplifying a radical

Example

Answer

Taking the Square Root of a Radical Expression

Answer

Answer

Answer

Answer

Answer

Answer

Answer

Writing Fractional Exponents

Answer

Answer

Answer

Answer

Writing a Square Root

The square root of a square

The Product Rule for Square Roots

Example

Answer

Answer

Example

Answer

Example

Answer

Cube Roots

Example

Answer

Example

Answer

Example

Answer

Example

Answer

Simplifying a radical

Example

Answer

Simplify Square Roots with Variables

Simplifying Square Roots

Taking the Square Root of a Radical Expression

Example

Answer

Example

Answer

Example

Answer

Rational Exponents

Convert Between Radical and Exponent Notation

Example

Answer

Example

Answer

Example

Answer

Example

Answer

Writing Fractional Exponents

Simplifying Radical Expressions Using Rational Exponents and the Laws of Exponents

Example

Answer

Example

Answer

Example

Answer

Example

Answer

Summary

Support Center

How can we help?