8.4: Solving Radical Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Solve Radical Equations
- Isolate square roots in equations and solve for a variable
- Identify extraneous solutions to radical equations
- Square Roots and Completing the Square for Solving Radical Equations
- Use square roots to solve quadratic equations
- Complete the square to solve a quadratic equation
- Using the Quadratic Formula to Solve Quadratic Equations
- Write a quadratic equation in standard form and identify the values of a, b, and c in a standard form quadratic equation.
- Use the Quadratic Formula to find all real solutions.
- Solve application problems requiring the use of the Quadratic Formula.
A basic strategy for solving radical equations is to isolate the radical term first, and then raise both sides of the equation to a power to remove the radical. (The reason for using powers will become clear in a moment.) This is the same type of strategy you used to solve other, non-radical equations—rearrange the expression to isolate the variable you want to know, and then solve the resulting equation.
Solutions to Radical Equations
The solutions of x2=a are called the square roots of a.
- When a is positive, a > 0, +√a,−√a. −√a is the negative square root of a.
- When a is negative, a < 0, x2=a has no solutions.
- When a is zero, a = 0, x2=a has one solution: a = 0
Just to drive home the importance of the concept that when a is negative, a < 0, x2=a has no solutions, we will restate it in words. If you have a negative number under a square root sign as in this example,
√−3
There will be no real number solutions.
There are two key ideas that you will be using to solve radical equations. The first is that if \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/p[5]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/p[5]/span[2], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/p[5]/span[3], line 1, column 1
Let’s start with a radical equation that you can solve in a few steps:√x−3=5.
Example
Solve. √x−3=5
[reveal-answer q=”946356″]Show Solution[/reveal-answer]
[hidden-answer a=”946356″]Add 3 to both sides to isolate the variable term on the left side of the equation.
√x−3=5+3+3_
Collect like terms.
√x=8
Square both sides to remove the radical, since \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[3]/p[6]/span, line 1, column 2
\(\begin{array}{r}
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[3]/p[7]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[3]/p[7]/span[2], line 1, column 2
Answer
√x−3=5
[/hidden-answer]
To check your solution, you can substitute 64 in for x in the original equation. Does 8−3=5.
Notice how you combined like terms and then squared both sides of the equation in this problem. This is a standard method for removing a radical from an equation. It is important to isolate a radical on one side of the equation and simplify as much as possible before squaring. The fewer terms there are before squaring, the fewer additional terms will be generated by the process of squaring.
In the example above, only the variable x was underneath the radical. Sometimes you will need to solve an equation that contains multiple terms underneath a radical. Follow the same steps to solve these, but pay attention to a critical point—square both sides of an equation, not individual terms. Watch how the next two problems are solved.
Example
Solve. x+8. Square both sides to remove the radical.
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[4]/p[2]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[4]/p[2]/span[2], line 1, column 1
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[4]/p[3]/span, line 1, column 1
x+8=9x=1
Check your answer. Substituting 1 for x in the original equation yields a true statement, so the solution is correct.
√1+8=3√9=33=3
Answer
√x+8=3.
[/hidden-answer]
In the following video we show how to solve simple radical equations.
Example
Solve. 1+√2x+3=6
[reveal-answer q=”479262″]Show Solution[/reveal-answer]
[hidden-answer a=”479262″]Begin by subtracting 1 from both sides in order to isolate the radical term. Then square both sides to remove the binomial from the radical.
\(\begin{array}{r}1+\sqrt{2x+3}-1=6-1\\\sqrt{2x+3}=5\,\,\,\,\,\,\,\,\,\,\\
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[5]/p[3]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[5]/p[3]/span[2], line 1, column 1
Simplify the equation and solve for x.
2x+3=252x=22x=11
Check your answer. Substituting 11 for x in the original equation yields a true statement, so the solution is correct.
1+√2(11)+3=61+√22+3=61+√25=61+5=66=6
Answer
1+√2x+3=6.
[/hidden-answer]
Solving Radical Equations
Follow the following four steps to solve radical equations.
- Isolate the radical expression.
- Square both sides of the equation: If x2=y2.
- Once the radical is removed, solve for the unknown.
- Check all answers.
Identify Extraneous Solutions
Following rules is important, but so is paying attention to the math in front of you—especially when solving radical equations. Take a look at this next problem that demonstrates a potential pitfall of squaring both sides to remove the radical.
Example
Solve. √a−5=−2
[reveal-answer q=”798652″]Show Solution[/reveal-answer]
[hidden-answer a=”798652″]Square both sides to remove the term a–5 from the radical.
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[1]/p[3]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[1]/p[3]/span[2], line 1, column 5
Write the simplified equation, and solve for a.
a−5=4a=9
Now check the solution by substituting a=9 into the original equation.
It does not check!
√9−5=−2√4=−22≠−2
Answer
No solution.
[/hidden-answer]
Look at that—the answer a=9 does not produce a true statement when substituted back into the original equation. What happened?
Check the original problem: −2, and recall that the principal square root of a number can only be positive. This means that no value for a will result in a radical expression whose positive square root is −2! You might have noticed that right away and concluded that there were no solutions for a.
Incorrect values of the variable, such as those that are introduced as a result of the squaring process are called extraneous solutions. Extraneous solutions may look like the real solution, but you can identify them because they will not create a true statement when substituted back into the original equation. This is one of the reasons why checking your work is so important—if you do not check your answers by substituting them back into the original equation, you may be introducing extraneous solutions into the problem.
In the next video example, we solve more radical equations that may have extraneous solutions.
Have a look at the following problem. Notice how the original problem is \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[1]/div/p[6]/span, line 1, column 2
Example
Solve. x+4=√x+10
[reveal-answer q=”705028″]Show Solution[/reveal-answer]
[hidden-answer a=”705028″]Square both sides to remove the term x+10 from the radical.
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[2]/p[3]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[2]/p[3]/span[2], line 1, column 1
Now simplify and solve the equation. Combine like terms, and then factor.
\(\begin{array}{r}\left( x+4 \right)\left( x+4 \right)=x+10\\
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[2]/p[5]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[2]/p[5]/span[2], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[2]/p[5]/span[3], line 1, column 2
Set each factor equal to zero and solve for x.
(x+6)=0or(x+1)=0x=−6 or x=−1
Now check both solutions by substituting them into the original equation.
Since x=−6 produces a false statement, it is an extraneous solution.
−6+4=√−6+10−2=√4−2=2FALSE!−1+4=√−1+103=√93=3TRUE!
Answer
x=−1 is the only solution
[/hidden-answer]
Example
Solve. 4+√x+2=x
[reveal-answer q=”568479″]Show Solution[/reveal-answer]
[hidden-answer a=”568479″]Isolate the radical term.
√x+2=x−4
Square both sides to remove the term x+2 from the radical.
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[3]/p[5]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[3]/p[5]/span[2], line 1, column 1
Now simplify and solve the equation. Combine like terms, and then factor.
\(\begin{array}{l}x+2=
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[3]/p[7]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[3]/p[7]/span[2], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[6]/div[3]/p[7]/span[3], line 1, column 2
Set each factor equal to zero and solve for x.
(x−7)=0 or (x−2)=0x=7 or x=2
Now check both solutions by substituting them into the original equation.
Since x=2 produces a false statement, it is an extraneous solution.
4+√7+2=74+√9=74+3=77=7TRUE!4+√2+2=24+√4=24+2=26=2FALSE!
Answer
x=7 is the only solution.
[/hidden-answer]
In the last video example we solve a radical equation with a binomial term on one side.
Square Roots and Completing the Square
Quadratic equations can be solved in many ways. In the previous section we introduced the idea that solutions to radical equations in general can be found using these facts:
Solutions to Quadratic Equations
The solutions of x2=a are called the square roots of a.
- When a is positive, a > 0, +√a,−√a. −√a is the negative square root of a.
- When a is negative, a < 0, x2=a has no solutions.
- When a is zero, a = 0, x2=a has one solution: a = 0
A shortcut way to write −√a is ± is often read “positive or negative.” If it is used as an operation (addition or subtraction), it is read “plus or minus.”
Example
Solve using the Square Root Property. x2=9
[reveal-answer q=”793132″]Show Solution[/reveal-answer]
[hidden-answer a=”793132″]Since one side is simply x2, you can take the square root of both sides to get x on one side. Don’t forget to use both positive and negative square roots!
x2=9x=±√9x=±3
Answer
x=3 or −3)
[/hidden-answer]
Notice that there is a difference here in solving √9. For √9, you only want the principal (nonnegative) square root. The negative of the principal square root is ±√9. Unless there is a symbol in front of the radical sign, only the nonnegative value is wanted!
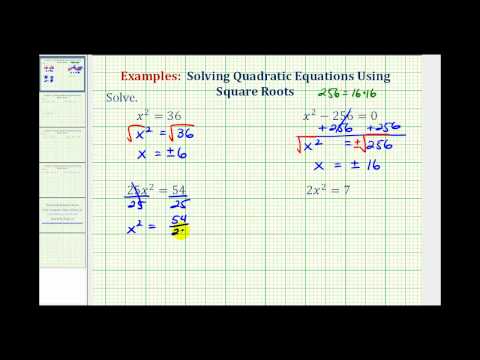
In the example above, you can take the square root of both sides easily because there is only one term on each side. In some equations, you may need to do some work to get the equation in this form. You will find that this involves isolating x2.
Example
Solve. 10x2+5=85
[reveal-answer q=”637209″]Show Solution[/reveal-answer]
[hidden-answer a=”637209″]If you try taking the square root of both sides of the original equation, you will have x2 term by itself.
10x2+5=85
You could now take the square root of both sides, but you would have √10 as a coefficient, and you would need to divide by that coefficient. Dividing by 10 before you take the square root will be a little easier.
10x2=80
Now you have only x2 on the left, so you can use the Square Root Property easily.
Be sure to simplify the radical if possible.
\(\begin{array}{l}
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[3]/p[8]/span, line 1, column 2
Answer
x=±2√2
[/hidden-answer]
In the following video we show more examples of solving simple quadratic equations using square roots.
Sometimes more than just the x is being squared:
Example
Solve. (x–2)2–50=0
[reveal-answer q=”347487″]Show Solution[/reveal-answer]
[hidden-answer a=”347487″]Again, taking the square root of both sides at this stage will leave something you can’t work with on the left. Start by adding 50 to both sides.
(x−2)2−50=0
Because (x–2)2 is a squared quantity, you can take the square root of both sides.
(x−2)2=50x−2=±√50
To isolate x on the left, you need to add 2 to both sides.
Be sure to simplify the radical if possible.
x=2±√50=2±√(25)(2)=2±√25√2=2±5√2
Answer
x=2±5√2
[/hidden-answer]
In this video example, you will see more examples of solving quadratic equations using square roots.
Completing the Square to Solve a Quadratic Equation
Of course, quadratic equations often will not come in the format of the examples above. Most of them will have x terms. However, you may be able to factor the expression into a squared binomial—and if not, you can still use squared binomials to help you.
Some of the above examples have squared binomials: (x–2)2 are squared binomials. If you expand these, you get a perfect square trinomial.
Perfect square trinomials have the form (x+s)2, or they have the form (x–s)2. Let’s factor a perfect square trinomial into a squared binomial.
Example
Factor 9x2–24x+16.
[reveal-answer q=”844629″]Show Solution[/reveal-answer]
[hidden-answer a=”844629″]First notice that the x2 term and the constant term are both perfect squares.
9x2=(3x)216=42
Then notice that the middle term (ignoring the sign) is twice the product of the square roots of the other terms.
24x=2(3x)(4)
A trinomial in the form (r–s)2.
In this case, the middle term is subtracted, so subtract r and s and square it to get (r–s)2.
r=3xs=49x2−24x+16=(3x−4)2
Answer
(3x–4)2
[/hidden-answer]
You can use the procedure in this next example to help you solve equations where you identify perfect square trinomials, even if the equation is not set equal to 0.
Example
Solve. 4x2+20x+25=8
[reveal-answer q=”538757″]Show Solution[/reveal-answer]
[hidden-answer a=”538757″]Since there’s an x term, you can’t use the Square Root Property immediately (or even after adding or dividing by a constant).
Notice, however, that the (2x)2 and 2(2x)(5)? Yes!
4x2+20x+25=8
A trinomial in the form (r+s)2, so rewrite the left side as a squared binomial.
(2x+5)2=8
Now you can use the Square Root Property. Some additional steps are needed to isolate x.
2x+5=±√82x=−5±√8x=−52±12√8
Simplify the radical when possible.
x=−52±12√4√2x=−52±12(2)√2x=−52±√2
Answer
x=−52±√2
[/hidden-answer]
One way to solve quadratic equations is by completing the square. When you don’t have a perfect square trinomial, you can create one by adding a constant term that is a perfect square to both sides of the equation. Let’s see how to find that constant term.
“Completing the square” does exactly what it says—it takes something that is not a square and makes it one. This idea can be illustrated using an area model of the binomial x2+bx.

In this example, the area of the overall rectangle is given by x(x+b).
Now let’s make this rectangle into a square. First, divide the red rectangle with area bx into two equal rectangles each with area bx.
The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[1]/p[7]/span, line 1, column 1
Here comes the cool part—do you see that when the white square is added to the blue and red regions, the whole shape is also now a square? In other words, you’ve “completed the square!” By adding the quantity x+b2.
Notice that the area of this square can be written as a squared binomial: (x+b2)2.
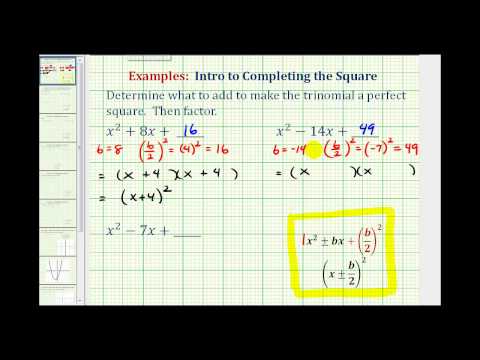
Finding a Value that will Complete the Square in an Expression
To complete the square for an expression of the form x2+bx:
- Identify the value of b;
- Calculate and add (b2)2.
The expression becomes x2+bx+(b2)2=(x+b2)2.
Example
Find the number to add to x2+8x to make it a perfect square trinomial.
[reveal-answer q=”691356″]Show Solution[/reveal-answer]
[hidden-answer a=”691356″]First identify b if this has the form x2+bx.
x2+8xb=8
To complete the square, add (b2)2.
(b2)2=(82)2
Simplify.
x2+8x+(4)2x2+8x+16
Check that the result is a perfect square trinomial. (x+4)2=x2+4x+4x+16=x2+8x+16, so it is.
Answer
Adding x2+8x a perfect square trinomial.
[/hidden-answer]
Notice that \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[2]/div/p[3]/span, line 1, column 1
In the following video, we show more examples of how to find a constant terms that will make a trinomial a perfect square.
You can use completing the square to help you solve a quadratic equation that cannot be solved by factoring.
Let’s start by seeing what happens when you complete the square in an equation. In the example below, notice that completing the square will result in adding a number to both sides of the equation—you have to do this in order to keep both sides equal!
Example
Rewrite x2+6x=8 so that the left side is a perfect square trinomial.
[reveal-answer q=”539170″]Show Solution[/reveal-answer]
[hidden-answer a=”539170″]This equation has a constant of 8. Ignore it for now and focus on the x2+bx, so you can identify b.
x2+6x=8b=6
To complete the square, add \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[3]/p[4]/span, line 1, column 1
\(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[3]/p[5]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[3]/p[5]/span[2], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[3]/p[5]/span[3], line 1, column 2
This is an equation, though, so you must add the same number to the right side as well.
x2+6x+9=8+9
Simplify. Check that the left side is a perfect square trinomial. (x+3)2=x2+3x+3x+9=x2+6x+9r, so it is.
x2+6x+9=17x2+6x+9=17(x+3)2=17
Answer
x2+6x+9=17
[/hidden-answer]
Can you see that completing the square in an equation is very similar to completing the square in an expression? The main difference is that you have to add the new number (+9 in this case) to both sides of the equation to maintain equality.
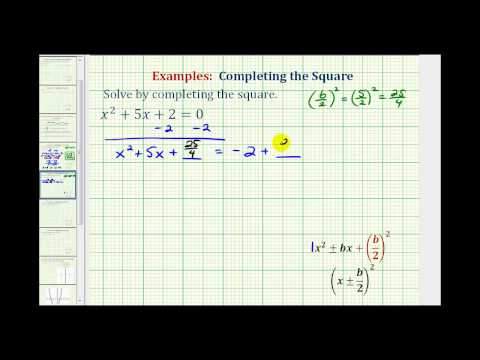
Now let’s look at an example where you are using completing the square to actually solve an equation, finding a value for the variable.
Example
Solve. x2–12x–4=0
[reveal-answer q=”903321″]Show Solution[/reveal-answer]
[hidden-answer a=”903321″]Since you cannot factor the trinomial on the left side, you will use completing the square to solve the equation.
Rewrite the equation with the left side in the form x2+bx, to prepare to complete the square. Identify b.
x2−12x=4b=−12
Figure out what value to add to complete the square. Add \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[4]/p[5]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[4]/p[5]/span[2], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[4]/p[5]/span[3], line 1, column 1
Add the value to both sides of the equation and simplify.
x2−12x+36=4+36x2−12x+36=40
Rewrite the left side as a squared binomial.
(x−6)2=40
Use the Square Root Property. Remember to include both the positive and negative square root, or you’ll miss one of the solutions.
x−6=±√40
Solve for x by adding 6 to both sides. Simplify as needed.
x=6±√40=6±√4√10=6±2√10
Answer
x=6±2√10
[/hidden-answer]
In this last video, we solve more quadratic equations by completing the square.
You may have noticed that because you have to use both square roots, all the examples have two solutions. Here is another example that’s slightly different.
Example
Solve x2+16x+17=−47.
[reveal-answer q=”270245″]Show Solution[/reveal-answer]
[hidden-answer a=”270245″]Rewrite the equation so the left side has the form x2+bx. Identify b.
x2+16x=−64b=16
Add \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[5]/p[4]/span[1], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[7]/div[7]/div[5]/p[4]/span[2], line 1, column 2
x2+16x+64=−64+64x2+16x+64=0
Write the left side as a squared binomial.
(x+8)2=0
Take the square roots of both sides. Normally both positive and negative square roots are needed, but 0 is neither positive nor negative. 0 has only one root.
x+8=0
Solve for x.
x=−8
Answer
x=−8
[/hidden-answer]
Take a closer look at this problem and you may see something familiar. Instead of completing the square, try adding 47 to both sides in the equation. The equation x2+16x+64=0. Can you factor this equation using grouping? (Think of two numbers whose product is 64 and whose sum is 16).
It can be factored as (x+8)(x+8)=0, of course! Knowing how to complete the square is very helpful, but it is not always the only way to solve an equation.
Use the Quadratic Formula to Solve Quadratic Equations

You can solve any quadratic equation by completing the square—rewriting part of the equation as a perfect square trinomial. If you complete the square on the generic equation \(x=\frac{-b\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[8]/p[1]/span, line 1, column 3
This formula is very helpful for solving quadratic equations that are difficult or impossible to factor, and using it can be faster than completing the square. The Quadratic Formula can be used to solve any quadratic equation of the form ax2+bx+c=0.
The form ax2+bx+c=0 is called standard form of a quadratic equation. Before solving a quadratic equation using the Quadratic Formula, it’s vital that you be sure the equation is in this form. If you don’t, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions.
Example
Rewrite the equation 3x+2x2+4=5 in standard form and identify a, b, and c.
[reveal-answer q=”489648″]Show Solution[/reveal-answer]
[hidden-answer a=”489648″]First be sure that the right side of the equation is 0. In this case, all you need to do is subtract 5 from both sides.
3x+2x2+4=53x+2x2+4–5=5–5
Simplify, and write the terms with the exponent on the variable in descending order.
3x+2x2−1=02x2+3x−1=0
Now that the equation is in standard form, you can read the values of a, b, and c from the coefficients and constant. Note that since the constant 1 is subtracted, c must be negative.
2x2+3x−1=0↓↓↓ax2bxca=2,b=3,c=−1
Answer
2x2+3x–1=0;a=2,b=3,c=−1
[/hidden-answer]
Example
Rewrite the equation 2(x+3)2–5x=6 in standard form and identify a, b, and c.
[reveal-answer q=”585220″]Show Solution[/reveal-answer]
[hidden-answer a=”585220″]First be sure that the right side of the equation is 0.
2(x+3)2–5x=62(x+3)2–5x–6=6–6
Expand the squared binomial, then simplify by combining like terms.
Be sure to write the terms with the exponent on the variable in descending order.
2(x2+6x+9)−5x−6=02x2+12x+18–5x–6=02x2+12x–5x+18–6=02x2+7x+12=0
Now that the equation is in standard form, you can read the values of a, b, and c from the coefficients and constant.
2x2+7x+12=0↓↓↓abca=2,b=7,c=7
Answer
2x2+7x+12=0;a=2,b=7,c=12
[/hidden-answer]
Solving a Quadratic Equation using the Quadratic Formula
The Quadratic Formula will work with any quadratic equation, but only if the equation is in standard form, ax2+bx+c=0. To use it, follow these steps.
- Put the equation in standard form first.
- Identify the coefficients, a, b, and c. Be careful to include negative signs if the bx or c terms are subtracted.
- Substitute the values for the coefficients into the Quadratic Formula.
- Simplify as much as possible.
- Use the ± in front of the radical to separate the solution into two values: one in which the square root is added, and one in which it is subtracted.
- Simplify both values to get the possible solutions.
That’s a lot of steps. Let’s try using the Quadratic Formula to solve a relatively simple equation first; then you’ll go back and solve it again using another factoring method.
Example
Use the Quadratic Formula to solve the equation x2+4x=5.
[reveal-answer q=”296770″]Show Solution[/reveal-answer]
[hidden-answer a=”296770″]First write the equation in standard form.
x2+4x=5x2+4x−5=0a=1,b=4,c=−5
Note that the subtraction sign means the constant c is negative.
\(\begin{array}{r}
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[1]/p[5]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[1]/p[5]/span[2], line 1, column 2
Substitute the values into the Quadratic Formula. \(x=\frac{-b\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[1]/p[6]/span, line 1, column 3
\(\begin{array}{l}\\x=\frac{-4\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[1]/p[7]/span, line 1, column 5
Simplify, being careful to get the signs correct.
x=−4±√16+202
Simplify some more.
x=−4±√362
Simplify the radical: √36=6.
x=−4±62
Separate and simplify to find the solutions to the quadratic equation. Note that in one, 6 is added and in the other, 6 is subtracted.
x=−4+62=22=1orx=−4−62=−102=−5
Answer
x=1or−5
[/hidden-answer]
You can check these solutions by substituting −5 into the original equation.
| x=−5x2+4x=5(−5)2+4(−5)=525−20=55=5 |
You get two true statements, so you know that both solutions work: −5. You’ve solved the equation successfully using the Quadratic Formula!
The power of the Quadratic Formula is that it can be used to solve any quadratic equation, even those where finding number combinations will not work.
In teh following video, we show an example of using the quadratic formula to solve an equation with two real solutions.
Most of the quadratic equations you’ve looked at have two solutions, like the one above. The following example is a little different.
Example
Use the Quadratic Formula to solve the equation x2−2x=6x−16.
[reveal-answer q=”998241″]Show Solution[/reveal-answer]
[hidden-answer a=”998241″]Subtract 6x from each side and add 16 to both sides to put the equation in standard form.
x2−2x=6x−16x2−2x−6x+16=0x2−8x+16=0
Identify the coefficients a, b, and c. a=1. Since a=1,b=−8,c=16
\(\begin{array}{r}
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[2]/p[5]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[2]/p[5]/span[2], line 1, column 2
Substitute the values into the Quadratic Formula.
\(\begin{array}{l}x=\frac{-b\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[2]/p[7]/span[1], line 1, column 3
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[9]/div[2]/p[7]/span[2], line 1, column 6
Simplify.
x=8±√64−642
Since the square root of 0 is 0, and both adding and subtracting 0 give the same result, there is only one possible value.
x=8±√02=82=4
Answer
x=4
[/hidden-answer]
Again, check using the original equation.
x2−2x=6x−16(4)2−2(4)=6(4)−1616−8=24−168=8
In the following video we show an example of using the quadratic formula to solve a quadratic equation that has one repeated solution.
In this video example we show that solutions to quadratic equations can have rational answers.
Applying the Quadratic Formula
Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.
A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation isn’t completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.
Example
A ball is thrown off a building from 200 feet above the ground. Its starting velocity (also called initial velocity) is −10 feet per second. (The negative value means it’s heading toward the ground.)
The equation h=−16t2−10t+200 can be used to model the height of the ball after t seconds. About how long does it take for the ball to hit the ground?
[reveal-answer q=”704677″]Show Solution[/reveal-answer]
[hidden-answer a=”704677″]When the ball hits the ground, the height is 0. Substitute 0 for h.
h=−16t2−10t+2000=−16t2−10t+200−16t2−10t+200=0
This equation is difficult to solve by factoring or by completing the square, so solve it by applying the Quadratic Formula, a=−16,b=−10, and c=200.
\(t=\frac{-(-10)\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[10]/div[1]/p[6]/span, line 1, column 7
Simplify. Be very careful with the signs.
t=10±√100+12800−32=10±√12900−32
Use a calculator to find both roots.
t is approximately 3.24.
Consider the roots logically. One solution, 3.24 seconds, must be when the ball hits the ground.
Answer
The ball hits the ground approximately 3.24 seconds after being thrown.
[/hidden-answer]
The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.
Example
Bob made a quilt that is 4 ft × 5 ft. He has 10 sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)
[reveal-answer q=”932211″]Show Solution[/reveal-answer]
[hidden-answer a=”932211″]Sketch the problem. Since you don’t know the width of the border, you will let the variable x represent the width.
In the diagram, the original quilt is indicated by the red rectangle. The border is the area between the red and blue lines.

Since each side of the original 4 by 5 quilt has the border of width x added, the length of the quilt with the border will be 4+2x.
(Both dimensions are written in terms of the same variable, and you will multiply them to get an area! This is where you might start to think that a quadratic equation might be used to solve this problem.)

You are only interested in the area of the border strips. Write an expression for the area of the border.
Area of border = Area of the blue rectangle minus the area of the red rectangle
Area of border=(4+2x)(5+2x)–(4)(5)
There are 10 sq ft of fabric for the border, so set the area of border to be 10.
10=(4+2x)(5+2x)–20
Multiply (4+2x)(5+2x).
10=20+8x+10x+4x2–20
Simplify.
10=18x+4x2
Subtract 10 from both sides so that you have a quadratic equation in standard form and can apply the Quadratic Formula to find the roots of the equation.
0=18x+4x2−10or4x2−102(2x2+9x−5)=0
Factor out the greatest common factor, 2, so that you can work with the simpler equivalent equation, 2x2+9x–5=0.
2(2x2+9x−5)=02(2x2+9x−5)2=022x2+9x−5=0
Use the Quadratic Formula. In this case, c=−5.
\(\begin{array}{l}x=\frac{-b\pm \sqrt
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[10]/div[2]/p[20]/span[1], line 1, column 3
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[10]/div[2]/p[20]/span[2], line 1, column 3
Simplify.
x=−9±√1214=−9±114
Find the solutions, making sure that the ± is evaluated for both values.
x=−9+114=24=12=0.5orx=−9−114=−204=−5
Ignore the solution x=−5, since the width could not be negative.
Answer
The width of the border should be 0.5 ft.
[/hidden-answer]
In this last video, we show how to use the quadratic formula to solve an application involving a picture frame.
Summary
A common method for solving radical equations is to raise both sides of an equation to whatever power will eliminate the radical sign from the equation. But be careful—when both sides of an equation are raised to an even power, the possibility exists that extraneous solutions will be introduced. When solving a radical equation, it is important to always check your answer by substituting the value back into the original equation. If you get a true statement, then that value is a solution; if you get a false statement, then that value is not a solution.
Completing the square is used to change a binomial of the form \(
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[11]/p[2]/span[1], line 1, column 2
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[11]/p[2]/span[2], line 1, column 1
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.04:_Solving_Radical_Equations), /content/body/div[11]/p[2]/span[3], line 1, column 1
Quadratic equations can appear in different applications. The Quadratic Formula is a useful way to solve these equations, or any other quadratic equation! The Quadratic Formula, " class="latex mathjax.
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Screenshot: Quadratic Equation. Provided by: Lumen Learning. License: CC BY: Attribution
- Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Ex 2: Solve Radical Equations - Square Roots. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/qkZHKK77grM. License: CC BY: Attribution
- Ex 1: Solve a Basic Radical Equation - Square Roots. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/tT0Zwsto6AQ. License: CC BY: Attribution
- Ex 4: Solve Radical Equations - Square Roots. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/y2yHPfuL0Hs. License: CC BY: Attribution
- Ex 2: Completing the Square - Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/IjCjbtrPWHM. License: CC BY: Attribution
- Ex: Creating a Perfect Square Quadratic Trinomial Expression. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/vt-pM1LEP1M. License: CC BY: Attribution
- Ex 2: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/4H5qZ_-8YM4. License: CC BY: Attribution
- Ex 1: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/Fj-BP7uaWrI. License: CC BY: Attribution
- Ex: Quadratic Formula - One Real Rational Repeated Solution. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/OXwwzWcxFgE. License: CC BY: Attribution
- Ex: Quadratic Equation App: Find the Width of a Frame (Factoring). Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/AlIoxXQ-V50. License: CC BY: Attribution
- Ex2: Quadratic Formula - Two Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/tF0muV86dr0. License: CC BY: Attribution
- Ex: Quadratic Formula - Two Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/xtwO-n8lRPw. License: CC BY: Attribution