8.5: Putting It Together- Roots and Rational Exponents
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the beginning of this module, we proposed that one of the most well known uses of roots and rational exponents is found in quadratic equations.
Quadratic equations, when graphed on the Cartesian coordinate plane, form the shape of a parabola. Parabolas are unique and interesting shapes because no matter how you stretch, shrink, or enlarge them, they are all identical to each other. What does that mean?
A parabola is the set of all points (x,y) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.
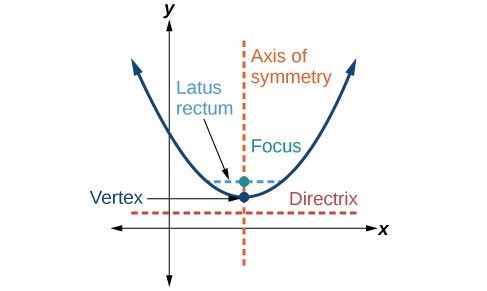
This feature of parabolas is what makes them so useful in so many ways, and what makes them identical to each other – this relationship holds no matter how you stretch or shrink them. Ellipses and circles do not share this quality. You can stretch and shrink them and they are not identical to each other. This unique fact about parabolas has some interesting impacts in our real lives.
For example, did you know that stage lighting and car headlamps are often parabolic in shape? The reason for this stems from the shape of the paraboloid.
According to Wikipedia, a parabolic (or paraboloid or paraboloidal) reflector (or dish or mirror) is a reflective surface used to collect or project energy such as light, sound, or radio waves.
Parabolic reflectors are used to collect energy from a distant source (for example sound waves or incoming star light) and bring it to a common focal point, as in the image below:
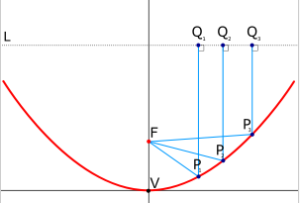
Since the principles of reflection are reversible, parabolic reflectors can also be used to project energy of a source at its focus outward in a parallel beam, used in devices such as spotlights and car headlights.

