12.3: The Dot Product
- Last updated
- Save as PDF
- Page ID
- 20187
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Calculate the dot product of two given vectors.
- Determine whether two given vectors are perpendicular.
- Find the direction cosines of a given vector.
- Explain what is meant by the vector projection of one vector onto another vector, and describe how to compute it.
- Calculate the work done by a given force.
If we apply a force to an object so that the object moves, we say that work is done by the force. Previously, we looked at a constant force and we assumed the force was applied in the direction of motion of the object. Under those conditions, work can be expressed as the product of the force acting on an object and the distance the object moves. In this chapter, however, we have seen that both force and the motion of an object can be represented by vectors.
In this section, we develop an operation called the dot product, which allows us to calculate work in the case when the force vector and the motion vector have different directions. The dot product essentially tells us how much of the force vector is applied in the direction of the motion vector. The dot product can also help us measure the angle formed by a pair of vectors and the position of a vector relative to the coordinate axes. It even provides a simple test to determine whether two vectors meet at a right angle.
The Dot Product and Its Properties
We have already learned how to add and subtract vectors. In this chapter, we investigate two types of vector multiplication. The first type of vector multiplication is called the dot product, based on the notation we use for it, and it is defined as follows:
Definition: dot product
The dot product of vectors \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) is given by the sum of the products of the components
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]
Note that if \(u\) and \(v\) are two-dimensional vectors, we calculate the dot product in a similar fashion. Thus, if \(\vecs{ u}=⟨u_1,u_2⟩\) and \(\vecs{ v}=⟨v_1,v_2⟩,\) then
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2. \nonumber \]
When two vectors are combined under addition or subtraction, the result is a vector. When two vectors are combined using the dot product, the result is a scalar. For this reason, the dot product is often called the scalar product. It may also be called the inner product.
Example \(\PageIndex{1}\): Calculating Dot Products
- Find the dot product of \(\vecs{ u}=⟨3,5,2⟩\) and \(\vecs{ v}=⟨−1,3,0⟩\).
- Find the scalar product of \(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) and \(\vecs{ q}=−2\hat{\textbf i}+\hat{\textbf j}+6\hat{\textbf k}.\)
Solution:
a. Substitute the vector components into the formula for the dot product:
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{align*}\]
b. The calculation is the same if the vectors are written using standard unit vectors. We still have three components for each vector to substitute into the formula for the dot product:
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18.\end{align*}\]
Exercise \(\PageIndex{1}\)
Find \(\vecs{ u}⋅\vecs{ v}\), where \(\vecs{ u}=⟨2,9,−1⟩\) and \(\vecs{ v}=⟨−3,1,−4⟩.\)
- Hint
-
Multiply corresponding components and then add their products.
- Answer
-
\(7\)
Like vector addition and subtraction, the dot product has several algebraic properties. We prove three of these properties and leave the rest as exercises.
Properties of the Dot Product
Let \(\vecs{ u}\), \(\vecs{ v}\), and \(\vecs{ w}\) be vectors, and let \(c\) be a scalar.
- Commutative property \[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
- Distributive property \[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \nonumber \]
- Associative property \[c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v}) \nonumber \]
- Property of magnitude \[\vecs{ v}⋅\vecs{ v}=\|\vecs{ v}\|^2 \nonumber \]
Proof
Let \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩.\) Then
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align*}\]
The associative property looks like the associative property for real-number multiplication, but pay close attention to the difference between scalar and vector objects:
\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2)+c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]
The proof that \(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\) is similar.
The fourth property shows the relationship between the magnitude of a vector and its dot product with itself:
\[ \begin{align*} \vecs{ v}⋅\vecs{ v} &=⟨v_1,v_2,v_3⟩⋅⟨v_1,v_2,v_3⟩\\[4pt] &=(v_1)^2+(v_2)^2+(v_3)^2 \\[4pt] &=\left[\sqrt{(v_1)^2+(v_2)^2+(v_3)^2}\right]^2 \\[4pt] &=\|\vecs{ v}\|^2.\end{align*}\]
□
Note that the definition of the dot product yields \(\vecs{ 0}⋅\vecs{ v}=0.\) By property iv. if \(\vecs{ v}⋅\vecs{ v}=0,\) then \(\vecs{ v}=\vecs{ 0}.\)
Example \(\PageIndex{2}\): Using Properties of the Dot Product
Let \(\vecs{ a}=⟨1,2,−3⟩\), \(\vecs{ b}=⟨0,2,4⟩\), and \( \vecs{ c} =⟨5,−1,3⟩\).
Find each of the following products.
- \(( \vecs{ a} ⋅ \vecs{ b}) \vecs{ c} \)
- \(\vecs{ a}⋅(2\vecs{ c})\)
- \(\|\vecs{ b}\|^2\)
Solution
a. Note that this expression asks for the scalar multiple of \(\vecs{ c}\) by \(\vecs{ a}⋅\vecs{ b}\):
\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=(1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]
b. This expression is a dot product of vector \(\vecs{ a}\) and scalar multiple 2\(\vecs{ c}\):
\[ \begin{align*} \vecs{ a}⋅(2\vecs{ c}) &=2(\vecs{ a}⋅\vecs{ c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\[4pt] &=2(1(5)+2(−1)+(−3)(3)) \\[4pt] &=2(−6)=−12.\end{align*}\]
c. Simplifying this expression is a straightforward application of the dot product:
\[ \begin{align*} \|\vecs{ b}\|^2 &=\vecs{ b}⋅\vecs{ b} \\[4pt] &=⟨0,2,4⟩⋅⟨0,2,4⟩\\[4pt] &=0^2+2^2+4^2\\[4pt] &=0+4+16\\[4pt] &=20.\end{align*}\]
Exercise \(\PageIndex{2}\)
Find the following products for \(\vecs{ p}=⟨7,0,2⟩\), \(\vecs{ q}=⟨−2,2,−2⟩\), and \(\vecs{ r}=⟨0,2,−3⟩\).
- \((\vecs{ r}⋅\vecs{ p})\vecs{ q}\)
- \(\|\vecs{ p}\|^2\)
- Hint
-
\(\vecs{ r}⋅\vecs{ p}\) is a scalar.
- Answer
-
\(a. \quad (\vecs{ r}⋅\vecs{ p})\vecs{ q}=⟨12,−12,12⟩; \quad b. \quad \|\vecs{ p}\|^2=53\)
Using the Dot Product to Find the Angle between Two Vectors
When two nonzero vectors are placed in standard position, whether in two dimensions or three dimensions, they form an angle between them (Figure \(\PageIndex{1}\)). The dot product provides a way to find the measure of this angle. This property is a result of the fact that we can express the dot product in terms of the cosine of the angle formed by two vectors.
Evaluating a Dot Product
The dot product of two vectors is the product of the magnitude of each vector and the cosine of the angle between them:
\[\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]
Proof
Place vectors \(\vecs{ u}\) and \(\vecs{ v}\) in standard position and consider the vector \(\vecs{ v}−\vecs{ u}\) (Figure \(\PageIndex{2}\)). These three vectors form a triangle with side lengths \(‖\vecs{ u}‖,‖\vecs{ v}‖\), and \(‖\vecs{ v}−\vecs{ u}‖\).
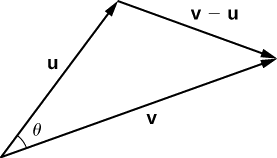
Recall from trigonometry that the law of cosines describes the relationship among the side lengths of the triangle and the angle \(θ\). Applying the law of cosines here gives
\[‖\vecs{ v}−\vecs{ u}‖^2=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{eq20} \]
The dot product provides a way to rewrite the left side of Equation \ref{eq20}:
\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=(\vecs{ v}−\vecs{ u})⋅(\vecs{ v}−\vecs{ u}) \\[4pt] &=(\vecs{ v}−\vecs{ u})⋅\vecs{ v}−(\vecs{ v}−\vecs{ u})⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ v}⋅\vecs{ u}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2.\end{align*}\]
Substituting into the law of cosines yields
\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] ‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2 &= ‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
□
We can use the form of the dot product in Equation \ref{evaldot} to find the measure of the angle between two nonzero vectors by rearranging Equation \ref{evaldot} to solve for the cosine of the angle:
\[\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}. \label{dot2} \]
Using this equation, we can find the cosine of the angle between two nonzero vectors. Since we are considering the smallest angle between the vectors, we assume \(0°≤θ≤180°\) (or \(0≤θ≤π\) if we are working in radians). The inverse cosine is unique over this range, so we are then able to determine the measure of the angle \(θ\).
Example \(\PageIndex{3}\): Finding the Angle between Two Vectors
Find the measure of the angle between each pair of vectors.
- \(\mathbf{\hat i} + \mathbf{\hat j} + \mathbf{\hat k}\) and \(2\mathbf{\hat i} – \mathbf{\hat j} – 3\mathbf{\hat k}\)
- \(⟨2,5,6⟩\) and \(⟨−2,−4,4⟩\)
Solution
a. To find the cosine of the angle formed by the two vectors, substitute the components of the vectors into Equation \ref{dot2}:
\[ \begin{align*} \cos θ &=\dfrac{(\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k})⋅(2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k})}{∥\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}∥⋅∥2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k}∥} \\[4pt] &=\dfrac{1(2)+(1)(−1)+(1)(−3)}{\sqrt{1^2+1^2+1^2}\sqrt{2^2+(−1)^2+(−3)^2}} \\[4pt] &=\dfrac{−2}{\sqrt{3}\sqrt{14}} =\dfrac{−2}{\sqrt{42}}. \end{align*}\]
Therefore, \(θ=\arccos\dfrac{−2}{\sqrt{42}}\) rad.
b. Start by finding the value of the cosine of the angle between the vectors:
\[ \begin{align*} \cos θ &=\dfrac{⟨2,5,6⟩⋅⟨−2,−4,4⟩}{∥⟨2,5,6⟩∥⋅∥⟨−2,−4,4⟩∥} \\[4pt] &=\dfrac{2(−2)+(5)(−4)+(6)(4)}{\sqrt{2^2+5^2+6^2}\sqrt{(−2)^2+(−4)^2+4^2}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
Now, \(\cos θ=0\) and \(0≤θ≤π\), so \(θ=π/2\).
Exercise \(\PageIndex{3}\)
Find the measure of the angle, in radians, formed by vectors \(\vecs{ a}=⟨1,2,0⟩\) and \(\vecs{ b}=⟨2,4,1⟩\). Round to the nearest hundredth.
- Hint
-
Use the Equation \ref{dot2}.
- Answer
-
\(θ≈0.22\) rad
The angle between two vectors can be acute \((0<\cos θ<1),\) obtuse \((−1<\cos θ<0)\), or straight \((\cos θ=−1)\). If \(\cos θ=1\), then both vectors have the same direction. If \(\cos θ=0\), then the vectors, when placed in standard position, form a right angle (Figure \(\PageIndex{3}\)). We can formalize this result into a theorem regarding orthogonal (perpendicular) vectors.
Orthogonal Vectors
The nonzero vectors \(\vecs{u}\) and \(\vecs{v}\) are orthogonal vectors if and only if \(\vecs{u}⋅\vecs{v}=0.\)
Proof
Let \(\vecs{u}\) and \(\vecs{v}\) be nonzero vectors, and let \(θ\) denote the angle between them. First, assume \(\vecs{u}⋅\vecs{v}=0.\)Then
\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]
However, \(‖\vecs{u}‖≠0\) and \(‖\vecs{v}‖≠0,\) so we must have \(\cos θ=0\). Hence, \(θ=90°\), and the vectors are orthogonal.
Now assume \(\vecs{u}\) and \(\vecs{v}\) are orthogonal. Then \(θ=90°\) and we have
\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0) \\[4pt] &=0. \end{align*}\]
□
The terms orthogonal, perpendicular, and normal each indicate that mathematical objects are intersecting at right angles. The use of each term is determined mainly by its context. We say that vectors are orthogonal and lines are perpendicular. The term normal is used most often when measuring the angle made with a plane or other surface.
Example \(\PageIndex{4}\): Identifying Orthogonal Vectors
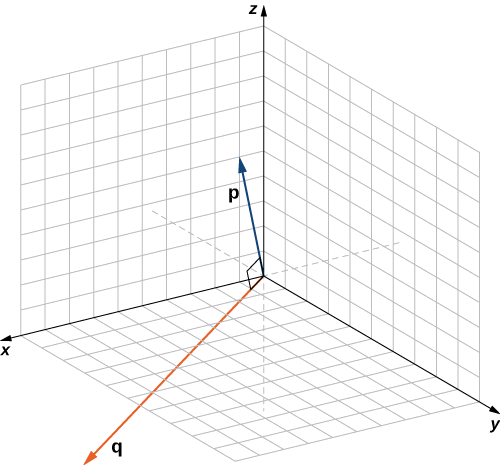
Determine whether \(\vecs{p}=⟨1,0,5⟩\) and \(\vecs{q}=⟨10,3,−2⟩\) are orthogonal vectors.
Solution
Using the definition, we need only check the dot product of the vectors:
\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+(5)(−2)=10+0−10=0. \nonumber \]
Because \(\vecs{p}⋅\vecs{q}=0,\) the vectors are orthogonal (Figure \(\PageIndex{4}\)).
Exercise \(\PageIndex{4}\)
For which value of \(x\) is \(\vecs{ p}=⟨2,8,−1⟩\) orthogonal to \(\vecs{ q}=⟨x,−1,2⟩\)?
- Hint
-
Vectors \(\vecs{ p}\) and \(\vecs{ q}\) are orthogonal if and only if \(\vecs{ p}⋅\vecs{ q}=0\).
- Answer
-
\(x=5\)
Example \(\PageIndex{5}\): Measuring the Angle Formed by Two Vectors
Let \(\vecs{ v}=⟨2,3,3⟩.\) Find the measures of the angles formed by the following vectors.
- \(\vecs{ v}\) and \(\mathbf{\hat i}\)
- \(\vecs{ v}\) and \(\mathbf{\hat j}\)
- \(\vecs{ v}\) and \(\mathbf{\hat k}\)
Solution
a.Let α be the angle formed by \(\vecs{ v}\) and \(\mathbf{\hat i}\):
\[ \begin{align*} \cos{α} &=\dfrac{\vecs{ v}⋅\mathbf{\hat i}}{‖\vecs{ v}‖⋅\|\mathbf{\hat i}\|}=\dfrac{⟨2,3,3⟩⋅⟨1,0,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{2}{\sqrt{22}} \\[4pt] α &=\arccos\dfrac{2}{\sqrt{22}}≈1.130\,\text{rad.} \end{align*}\]
b. Let β represent the angle formed by \(\vecs{ v}\) and \(\mathbf{\hat j}\):
\[ \begin{align*} \cos{β} &=\dfrac{\vecs{ v}⋅\mathbf{\hat j}}{‖\vecs{ v}‖⋅\|\mathbf{\hat j}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,1,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt] β &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]
c. Let γ represent the angle formed by \(\vecs{ v}\) and \(\mathbf{\hat k}\):
\[ \begin{align*} \cos{γ} &=\dfrac{\vecs{ v}⋅\mathbf{\hat k}}{‖\vecs{ v}‖⋅\|\mathbf{\hat k}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,0,1⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]
Exercise \(\PageIndex{5}\)
Let \(\vecs{ v}=⟨3,−5,1⟩.\) Find the measure of the angles formed by each pair of vectors.
- \(\vecs{ v}\) and \(\mathbf{\hat i}\)
- \(\vecs{ v}\) and \(\mathbf{\hat j}\)
- \(\vecs{ v}\) and \(\mathbf{\hat k}\)
- Hint
-
\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\) and \(\mathbf{\hat k}=⟨0,0,1⟩\)
- Answer
-
\(a. α≈1.04\) rad; b. \(β≈2.58\) rad; c. \(γ≈1.40\) rad
The angle a vector makes with each of the coordinate axes, called a direction angle, is very important in practical computations, especially in a field such as engineering. For example, in astronautical engineering, the angle at which a rocket is launched must be determined very precisely. A very small error in the angle can lead to the rocket going hundreds of miles off course. Direction angles are often calculated by using the dot product and the cosines of the angles, called the direction cosines. Therefore, we define both these angles and their cosines.
Definition: direction angles
The angles formed by a nonzero vector and the coordinate axes are called the direction angles for the vector (Figure \(\PageIndex{5}\)). The cosines for these angles are called the direction cosines.
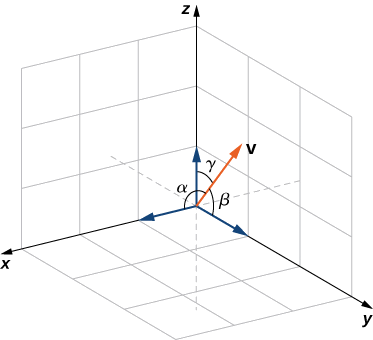
In Example \(\PageIndex{5}\), the direction cosines of \(\vecs{ v}=⟨2,3,3⟩\) are \(\cos α=\dfrac{2}{\sqrt{22}}, \cos β=\dfrac{3}{\sqrt{22}},\) and \(\cos γ=\dfrac{3}{\sqrt{22}}\). The direction angles of \(\vecs{ v}\) are \(α=1.130\) rad, \(β=0.877\) rad, and \(γ=0.877\) rad.
So far, we have focused mainly on vectors related to force, movement, and position in three-dimensional physical space. However, vectors are often used in more abstract ways. For example, suppose a fruit vendor sells apples, bananas, and oranges. On a given day, he sells 30 apples, 12 bananas, and 18 oranges. He might use a quantity vector, \(\vecs{ q}=⟨30,12,18⟩,\) to represent the quantity of fruit he sold that day. Similarly, he might want to use a price vector, \(\vecs{ p}=⟨0.50,0.25,1⟩,\) to indicate that he sells his apples for 50¢ each, bananas for 25¢ each, and oranges for $1 apiece. In this example, although we could still graph these vectors, we do not interpret them as literal representations of position in the physical world. We are simply using vectors to keep track of particular pieces of information about apples, bananas, and oranges.
This idea might seem a little strange, but if we simply regard vectors as a way to order and store data, we find they can be quite a powerful tool. Going back to the fruit vendor, let’s think about the dot product, \(\vecs{ q}⋅\vecs{ p}\). We compute it by multiplying the number of apples sold (30) by the price per apple (50¢), the number of bananas sold by the price per banana, and the number of oranges sold by the price per orange. We then add all these values together. So, in this example, the dot product tells us how much money the fruit vendor had in sales on that particular day.
When we use vectors in this more general way, there is no reason to limit the number of components to three. What if the fruit vendor decides to start selling grapefruit? In that case, he would want to use four-dimensional quantity and price vectors to represent the number of apples, bananas, oranges, and grapefruit sold, and their unit prices. As you might expect, to calculate the dot product of four-dimensional vectors, we simply add the products of the components as before, but the sum has four terms instead of three.
Example \(\PageIndex{6}\): Using Vectors in an Economic Context
AAA Party Supply Store sells invitations, party favors, decorations, and food service items such as paper plates and napkins. When AAA buys its inventory, it pays 25¢ per package for invitations and party favors. Decorations cost AAA 50¢ each, and food service items cost 20¢ per package. AAA sells invitations for $2.50 per package and party favors for $1.50 per package. Decorations sell for $4.50 each and food service items for $1.25 per package.
During the month of May, AAA Party Supply Store sells 1258 invitations, 342 party favors, 2426 decorations, and 1354 food service items. Use vectors and dot products to calculate how much money AAA made in sales during the month of May. How much did the store make in profit?
Solution
The cost, price, and quantity vectors are
\[ \begin{align*} \vecs{ c} &=⟨0.25,0.25,0.50,0.20⟩ \\[4pt] \vecs{ p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{ q} &=⟨1258,342,2426,1354⟩. \end{align*}\]
AAA sales for the month of May can be calculated using the dot product \(\vecs{ p}⋅\vecs{ q}\). We have
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=3145+513+10917+1692.5 \\[4pt] &= 16267.5. \end{align*}\]
So, AAA took in $16,267.50 during the month of May. To calculate the profit, we must first calculate how much AAA paid for the items sold. We use the dot product \(\vecs{c}⋅\vecs{q}\) to get
\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0.25,0.25,0.50,0.20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314.5+85.5+1213+270.8 \\[4pt] &=1883.8. \end{align*}\]
So, AAA paid $1,883.80 for the items they sold. Their profit, then, is given by
\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267.5−1883.8 =14383.7. \nonumber \]
Therefore, AAA Party Supply Store made $14,383.70 in May.
Exercise \(\PageIndex{6}\)
On June 1, AAA Party Supply Store decided to increase the price they charge for party favors to $2 per package. They also changed suppliers for their invitations, and are now able to purchase invitations for only 10¢ per package. All their other costs and prices remain the same. If AAA sells 1408 invitations, 147 party favors, 2112 decorations, and 1894 food service items in the month of June, use vectors and dot products to calculate their total sales and profit for June.
- Hint
-
Use four-dimensional vectors for cost, price, and quantity sold.
- Answer
-
Sales = $15,685.50; profit = $14,073.15
Projections
As we have seen, addition combines two vectors to create a resultant vector. But what if we are given a vector and we need to find its component parts? We use vector projections to perform the opposite process; they can break down a vector into its components. The magnitude of a vector projection is a scalar projection. For example, if a child is pulling the handle of a wagon at a 55° angle, we can use projections to determine how much of the force on the handle is actually moving the wagon forward (\(\PageIndex{6}\)). We return to this example and learn how to solve it after we see how to calculate projections.
Definition: Vector and Projection
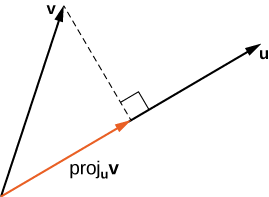
The vector projection of \(\vecs{ v}\) onto \(\vecs{ u}\) is the vector labeled \(\text{proj}_\vecs{ u}\vecs{ v}\) in Figure \(\PageIndex{7}\). It has the same initial point as \(\vecs{ u}\) and \(\vecs{ v}\) and the same direction as \(\vecs{ u}\), and represents the component of \(\vecs{ v}\) that acts in the direction of \(\vecs{ u}\). If \(θ\) represents the angle between \(\vecs{ u}\) and \(\vecs{ v}\), then, by properties of triangles, we know the length of \(\text{proj}_\vecs{ u}\vecs{ v}\) is \(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) When expressing \(\cos θ\) in terms of the dot product, this becomes
\[ \|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs v‖\cos θ=‖\vecs{ v}‖\left(\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]
We now multiply by a unit vector in the direction of \(\vecs{ u}\) to get \(\text{proj}_\vecs{ u}\vecs{ v}\):
\[\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\left(\dfrac{1}{‖\vecs{ u}‖}\vecs{ u}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}. \nonumber \]
The length of this vector is also known as the scalar projection of \(\vecs{ v}\) onto \(\vecs{ u}\) and is denoted by
\[\|\text{proj}_\vecs{ u}\vecs{ v}\|=\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]
Example \(\PageIndex{7}\): Finding Projections
Find the projection of \(\vecs{ v}\) onto \(\vecs{ u}\).
- \(\vecs{v}=⟨3,5,1⟩\) and \(\vecs{u}=⟨−1,4,3⟩\)
- \(\vecs{v}=3\mathbf{\hat i}−2\mathbf{\hat j}\) and \(\vecs{u}=\mathbf{\hat i}+6\mathbf{\hat j}\)
Solution
a. Substitute the components of \(\vecs{ v}\) and \(\vecs{ u}\) into the formula for the projection:
\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨−1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{−3+20+3}{(−1)^2+4^2+3^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4,3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{align*}\]
b. To find the two-dimensional projection, simply adapt the formula to the two-dimensional case:
\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{(\mathbf{\hat i}+6\mathbf{\hat j})⋅(3\mathbf{\hat i}−2\mathbf{\hat j})}{∥\mathbf{\hat i}+6\mathbf{\hat j}∥^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= \dfrac{1(3)+6(−2)}{1^2+6^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}\mathbf{\hat i}−\dfrac{54}{37}\mathbf{\hat j}.\end{align*}\]
Sometimes it is useful to decompose vectors—that is, to break a vector apart into a sum. This process is called the resolution of a vector into components. Projections allow us to identify two orthogonal vectors having a desired sum. For example, let \(\vecs{ v}=⟨6,−4⟩\) and let \(\vecs{ u}=⟨3,1⟩.\) We want to decompose the vector \(\vecs{ v}\) into orthogonal components such that one of the component vectors has the same direction as \(\vecs{ u}\).
We first find the component that has the same direction as \(\vecs{ u}\) by projecting \(\vecs{ v}\) onto \(\vecs{ u}\). Let \(\vecs{ p}=\text{proj}_\vecs{ u}\vecs{ v}\). Then, we have
\[\begin{align*}\vecs{ p} =\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}=\dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]
Now consider the vector \(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) We have
\[\begin{align*} \vecs{ q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]
Clearly, by the way we defined \(\vecs{ q}\), we have \(\vecs{ v}=\vecs{ q}+\vecs{ p},\) and
\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{189}{25}−\dfrac{189}{25}=0. \end{align*}\]
Therefore, \(\vecs{ q}\) and \(\vecs{ p}\) are orthogonal.
Example \(\PageIndex{8}\): Resolving Vectors into Components
Express \(\vecs{ v}=⟨8,−3,−3⟩\) as a sum of orthogonal vectors such that one of the vectors has the same direction as \(\vecs{ u}=⟨2,3,2⟩.\)
Solution
Let \(\vecs{ p}\) represent the projection of \(\vecs{ v}\) onto \(\vecs{ u}\):
\[ \begin{align*} \vecs{ p} &=\text{proj}_\vecs{ u}\vecs{ v} \\[4pt] &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨2,3,2⟩⋅⟨8,−3,−3⟩}{∥⟨2,3,2⟩∥^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{16−9−6}{2^2+3^2+2^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]
Then,
\[ \begin{align*} \vecs{ q} &=\vecs{ v}−\vecs{ p}=⟨8,−3,−3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]
To check our work, we can use the dot product to verify that \(\vecs{ p}\) and \(\vecs{ q}\) are orthogonal vectors:
\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}−\dfrac{162}{289}−\dfrac{106}{289}=0. \end{align*} \nonumber \]
Then,
\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \nonumber \]
Exercise \(\PageIndex{7}\)
Express \(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) as a sum of orthogonal vectors such that one of the vectors has the same direction as \(\vecs{ u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).
- Hint
-
Start by finding the projection of \(\vecs{ v}\) onto \(\vecs{ u}\).
- Answer
-
\(\vecs{ v}=\vecs{ p}+\vecs{ q},\) where \(\vecs{ p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac{9}{5}\mathbf{\hat j}\) and \(\vecs{ q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf{\hat j}\)
Example \(\PageIndex{9}\): Scalar Projection of Velocity
A container ship leaves port traveling \(15°\) north of east. Its engine generates a speed of 20 knots along that path (see the following figure). In addition, the ocean current moves the ship northeast at a speed of 2 knots. Considering both the engine and the current, how fast is the ship moving in the direction \(15°\) north of east? Round the answer to two decimal places.
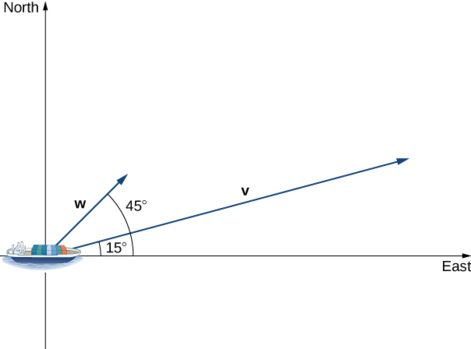
Solution
Let \(\vecs{ v}\) be the velocity vector generated by the engine, and let \(\vecs{w}\) be the velocity vector of the current. We already know \(‖\vecs{ v}‖=20\) along the desired route. We just need to add in the scalar projection of \(\vecs{ w}\) onto \(\vecs{ v}\). We get
\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{ w}=\dfrac{\vecs{ v}⋅\vecs{ w}}{‖\vecs{ v}‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖\cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1.73\,\text{knots.}\end{align*}\]
The ship is moving at 21.73 knots in the direction \(15°\) north of east.
Exercise \(\PageIndex{8}\)
Repeat the previous example, but assume the ocean current is moving southeast instead of northeast, as shown in the following figure.
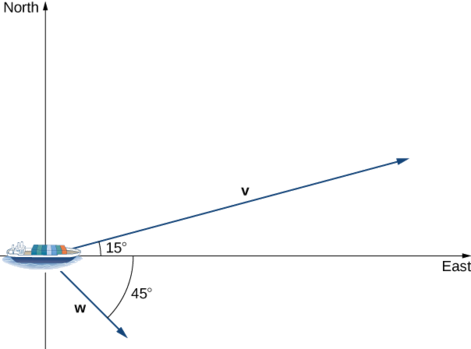
- Hint
-
Compute the scalar projection of \(\vecs{ w}\) onto \(\vecs{ v}\).
- Answer
-
21 knots
Work
Now that we understand dot products, we can see how to apply them to real-life situations. The most common application of the dot product of two vectors is in the calculation of work.
From physics, we know that work is done when an object is moved by a force. When the force is constant and applied in the same direction the object moves, then we define the work done as the product of the force and the distance the object travels: \(W=Fd\). We saw several examples of this type in earlier chapters. Now imagine the direction of the force is different from the direction of motion, as with the example of a child pulling a wagon. To find the work done, we need to multiply the component of the force that acts in the direction of the motion by the magnitude of the displacement. The dot product allows us to do just that. If we represent an applied force by a vector \(\vecs{ F}\) and the displacement of an object by a vector \(\vecs{ s}\), then the work done by the force is the dot product of \(\vecs{ F}\) and \(\vecs{ s}\).
Definition: Constant Force
When a constant force is applied to an object so the object moves in a straight line from point \(P\) to point \(Q\), the work \(W\) done by the force \(\vecs{ F}\), acting at an angle θ from the line of motion, is given by
\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ. \nonumber \]
Let’s revisit the problem of the child’s wagon introduced earlier. Suppose a child is pulling a wagon with a force having a magnitude of 8 lb on the handle at an angle of 55°. If the child pulls the wagon 50 ft, find the work done by the force (Figure \(\PageIndex{8}\)).
We have
\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb.} \nonumber \]
In U.S. standard units, we measure the magnitude of force \(∥\vecs{ F}∥\) in pounds. The magnitude of the displacement vector \(∥\vecd{PQ}∥\) tells us how far the object moved, and it is measured in feet. The customary unit of measure for work, then, is the foot-pound. One foot-pound is the amount of work required to move an object weighing 1 lb a distance of 1 ft straight up. In the metric system, the unit of measure for force is the newton (N), and the unit of measure of magnitude for work is a newton-meter (N·m), or a joule (J).
Example \(\PageIndex{10}\): Calculating Work
A conveyor belt generates a force \(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}\) that moves a suitcase from point \((1,1,1)\) to point \((9,4,7)\) along a straight line. Find the work done by the conveyor belt. The distance is measured in meters and the force is measured in newtons.
Solution
The displacement vector \(\vecd{PQ}\) has initial point \((1,1,1)\) and terminal point \((9,4,7)\):
\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}. \nonumber \]
Work is the dot product of force and displacement:
\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k})⋅(8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]
Exercise \(\PageIndex{9}\)
A constant force of 30 lb is applied at an angle of 60° to pull a handcart 10 ft across the ground. What is the work done by this force?
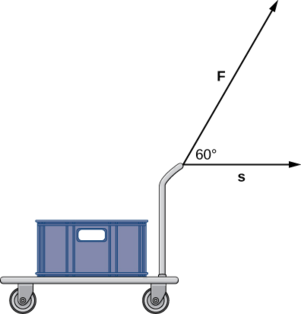
- Hint
-
Use the definition of work as the dot product of force and distance.
- Answer
-
150 ft-lb
Key Concepts
- The dot product, or scalar product, of two vectors \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) is \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\).
- The dot product satisfies the following properties:
- \(\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u}\)
- \(\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w}\)
- \(c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v})\)
- \(\vecs{ v}⋅\vecs{ v}=‖\vecs{ v}‖^2\)
- The dot product of two vectors can be expressed, alternatively, as \(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) This form of the dot product is useful for finding the measure of the angle formed by two vectors.
- Vectors \(\vecs{ u}\) and \(\vecs{ v}\) are orthogonal if \(\vecs{ u}⋅\vecs{ v}=0\).
- The angles formed by a nonzero vector and the coordinate axes are called the direction angles for the vector. The cosines of these angles are known as the direction cosines.
- The vector projection of \(\vecs{ v}\) onto \(\vecs{ u}\) is the vector \(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\). The magnitude of this vector is known as the scalar projection of \(\vecs{ v}\) onto \(\vecs{ u}\), given by \(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\).
- Work is done when a force is applied to an object, causing displacement. When the force is represented by the vector \(\vecs{ F}\) and the displacement is represented by the vector \(\vecs{ s}\), then the work done \(W\) is given by the formula \(W=\vecs{ F}⋅\vecs{ s}=∥\vecs{ F}∥‖\vecs{ s}‖\cos θ.\)
Key Equations
- Dot product of \(\vecs{ u}\) and \(\vecs{ v}\)
\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)
- Cosine of the angle formed by \(\vecs{ u}\) and \(\vecs{ v}\)
\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\)
- Vector projection of \(\vecs{ v}\) onto \(\vecs{ u}\)
\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\)
- Scalar projection of \(\vecs{ v}\) onto \(\vecs{ u}\)
\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\)
- Work done by a force \(\vecs{ F}\) to move an object through displacement vector \(\vecd{PQ}\)
\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)
Glossary
- direction angles
- the angles formed by a nonzero vector and the coordinate axes
- direction cosines
- the cosines of the angles formed by a nonzero vector and the coordinate axes
- dot product or scalar product
- \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\) where \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) and \(\vecs{ v}=⟨v_1,v_2,v_3⟩\)
- scalar projection
- the magnitude of the vector projection of a vector
- orthogonal vectors
- vectors that form a right angle when placed in standard position
- vector projection
- the component of a vector that follows a given direction
- work done by a force
- work is generally thought of as the amount of energy it takes to move an object; if we represent an applied force by a vector \(\vecs{ F}\) and the displacement of an object by a vector \(\vecs{ s}\), then the work done by the force is the dot product of \(\vecs{ F}\) and \(\vecs{ s}\).
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- edited for vector notation by Paul Seeburger

