6.4: Systems of Nonlinear Equations and Inequalities - Two Variables
- Last updated
- Dec 16, 2019
- Save as PDF
- Page ID
- 29148
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Solve a system of nonlinear equations using substitution.
- Solve a system of nonlinear equations using elimination.
- Graph a nonlinear inequality.
- Graph a system of nonlinear inequalities.
Halley’s Comet (Figure 6.4.1) orbits the sun about once every 75 years. Its path can be considered to be a very elongated ellipse. Other comets follow similar paths in space. These orbital paths can be studied using systems of equations. These systems, however, are different from the ones we considered in the previous section because the equations are not linear.

In this section, we will consider the intersection of a parabola and a line, a circle and a line, and a circle and an ellipse. The methods for solving systems of nonlinear equations are similar to those for linear equations.
Solving a System of Nonlinear Equations Using Substitution
A system of nonlinear equations is a system of two or more equations in two or more variables containing at least one equation that is not linear. Recall that a linear equation can take the form Ax+By+C=0. Any equation that cannot be written in this form in nonlinear. The substitution method we used for linear systems is the same method we will use for nonlinear systems. We solve one equation for one variable and then substitute the result into the second equation to solve for another variable, and so on. There is, however, a variation in the possible outcomes.
Intersection of a Parabola and a Line
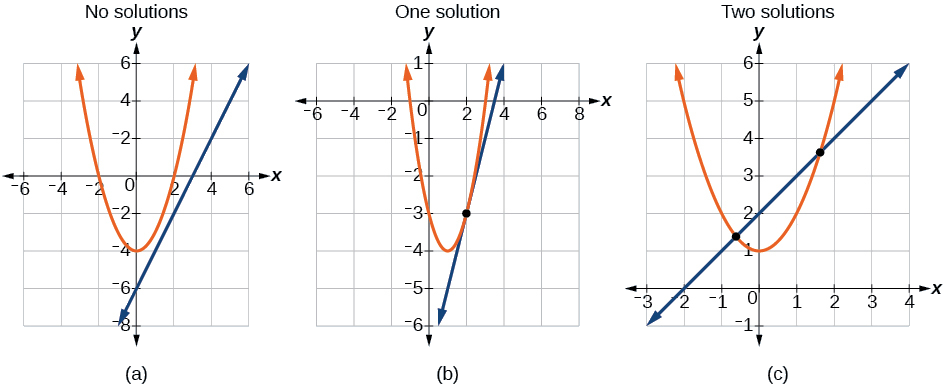
There are three possible types of solutions for a system of nonlinear equations involving a parabola and a line.
Possible Types of Solutions For Points of Intersection of a Parabola and a Line
Figure 6.4.2 illustrates possible solution sets for a system of equations involving a parabola and a line.
- No solution - The line will never intersect the parabola.
- One solution - The line is tangent to the parabola and intersects the parabola at exactly one point.
- Two solutions - The line crosses on the inside of the parabola and intersects the parabola at two points.
How to: Given a system of equations containing a line and a parabola, find the solution
- Solve the linear equation for one of the variables.
- Substitute the expression obtained in step one into the parabola equation.
- Solve for the remaining variable.
- Check your solutions in both equations.
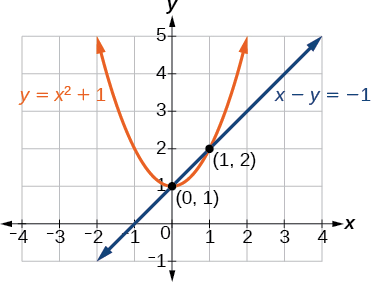
Example 6.4.1: Solving a System of Nonlinear Equations Representing a Parabola and a Line
Solve the system of equations.
x−y=−1y=x2+1
Solution
Solve the first equation for x and then substitute the resulting expression into the second equation.
x−y=−1x=y−1Solve for x.y=x2+1y=(y−1)2+1Substitute expression for x.
Expand the equation and set it equal to zero.
y=(y−1)2+1=(y2−2y+1)+1=y2−2y+20=y2−3y+2=(y−2)(y−1)
Solving for y gives y=2 and y=1. Next, substitute each value for y into the first equation to solve for x. Always substitute the value into the linear equation to check for extraneous solutions.
x−y=−1x−(2)=−1x=1x−(1)=−1x=0
The solutions are (1,2) and (0,1),which can be verified by substituting these (x,y) values into both of the original equations (Figure 6.4.3).
Q&A: Could we have substituted values for y into the second equation to solve for x in last example?
Yes, but because x is squared in the second equation this could give us extraneous solutions for x.
For y=1
y=x2+1y=x2+1x2=0x=±√0=0
This gives us the same value as in the solution.
For y=2
y=x2+12=x2+1x2=1x=±√1=±1
Notice that −1 is an extraneous solution.
Exercise 6.4.1
Solve the given system of equations by substitution.
3x−y=−22x2−y=0
- Answer
-
(−12,12) and (2,8)
Intersection of a Circle and a Line
Just as with a parabola and a line, there are three possible outcomes when solving a system of equations representing a circle and a line.
POSSIBLE TYPES OF SOLUTIONS FOR THE POINTS OF INTERSECTION OF A CIRCLE AND A LINE
Figure 6.4.4 illustrates possible solution sets for a system of equations involving a circle and a line.
- No solution - The line does not intersect the circle.
- One solution - The line is tangent to the circle and intersects the circle at exactly one point.
- Two solutions - The line crosses the circle and intersects it at two points.

How to: Given a system of equations containing a line and a circle, find the solution
- Solve the linear equation for one of the variables.
- Substitute the expression obtained in step one into the equation for the circle.
- Solve for the remaining variable.
- Check your solutions in both equations.
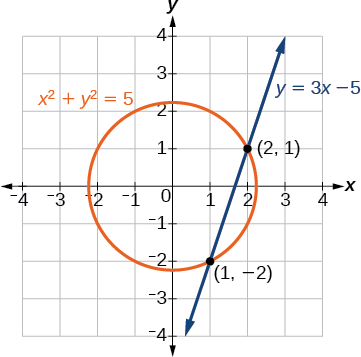
Example 6.4.2: Finding the Intersection of a Circle and a Line by Substitution
Find the intersection of the given circle and the given line by substitution.
x2+y2=5y=3x−5
Solution
One of the equations has already been solved for y. We will substitute y=3x−5 into the equation for the circle.
x2+(3x−5)2=5x2+9x2−30x+25=510x2−30x+20=0
Now, we factor and solve for x.
10(x2−3x+2)=010(x−2)(x−1)=0x=2x=1
Substitute the two x-values into the original linear equation to solve for y.
y=3(2)−5=1y=3(1)−5=−2
The line intersects the circle at (2,1) and (1,−2),which can be verified by substituting these (x,y) values into both of the original equations (Figure 6.4.5).
Exercise 6.4.2
Solve the system of nonlinear equations.
x2+y2=10x−3y=−10
- Answer
-
(−1,3)
Solving a System of Nonlinear Equations Using Elimination
We have seen that substitution is often the preferred method when a system of equations includes a linear equation and a nonlinear equation. However, when both equations in the system have like variables of the second degree, solving them using elimination by addition is often easier than substitution. Generally, elimination is a far simpler method when the system involves only two equations in two variables (a two-by-two system), rather than a three-by-three system, as there are fewer steps. As an example, we will investigate the possible types of solutions when solving a system of equations representing a circle and an ellipse.
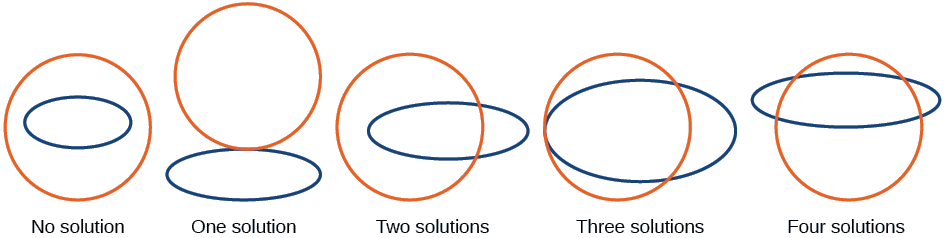
POSSIBLE TYPES OF SOLUTIONS FOR THE POINTS OF INTERSECTION OF A CIRCLE AND AN ELLIPSE
Figure 6.4.6 illustrates possible solution sets for a system of equations involving a circle and an ellipse.
- No solution - The circle and ellipse do not intersect. One shape is inside the other or the circle and the ellipse are a distance away from the other.
- One solution - The circle and ellipse are tangent to each other, and intersect at exactly one point.
- Two solutions - The circle and the ellipse intersect at two points.
- Three solutions - The circle and the ellipse intersect at three points.
- Four solutions - The circle and the ellipse intersect at four points.
Example 6.4.3: Solving a System of Nonlinear Equations Representing a Circle and an Ellipse
Solve the system of nonlinear equations.
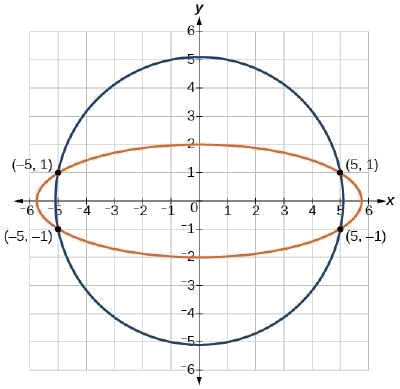
x2+y2=26(1)3x2+25y2=100(2)
Solution
Let’s begin by multiplying equation (1) by −3,and adding it to equation (2).
(−3)(x2+y2)=(−3)(26)−3x2−3y2=−783x2+25y2=100_22y2=22
After we add the two equations together, we solve for y.
y2=1y=±√1=±1
Substitute y=±1 into one of the equations and solve for x.
x2+(1)2=26x2+1=26x2=25x=±√25=±5x2+(−1)2=26x2+1=26x2=±√25=±5
There are four solutions: (5,1), (−5,1), (5,−1),and (−5,−1). See Figure 6.4.7.
Exercise 6.4.3
Find the solution set for the given system of nonlinear equations.
4x2+y2=13x2+y2=10
- Answer
-
(1,3),(1,−3),(−1,3),(−1,−3)
Graphing a Nonlinear Inequality
All of the equations in the systems that we have encountered so far have involved equalities, but we may also encounter systems that involve inequalities. We have already learned to graph linear inequalities by graphing the corresponding equation, and then shading the region represented by the inequality symbol. Now, we will follow similar steps to graph a nonlinear inequality so that we can learn to solve systems of nonlinear inequalities. A nonlinear inequality is an inequality containing a nonlinear expression. Graphing a nonlinear inequality is much like graphing a linear inequality.
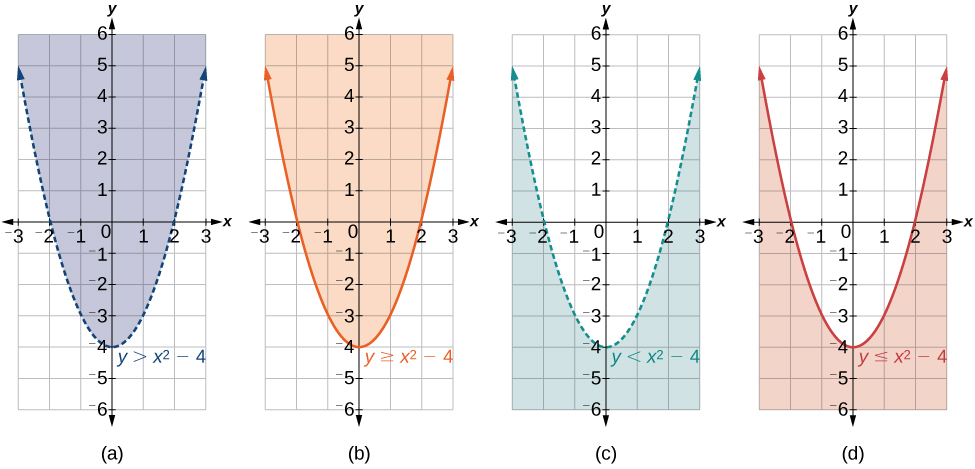
Recall that when the inequality is greater than, y>a,or less than, y<a,the graph is drawn with a dashed line. When the inequality is greater than or equal to, y≥a,or less than or equal to, y≤a,the graph is drawn with a solid line. The graphs will create regions in the plane, and we will test each region for a solution. If one point in the region works, the whole region works. That is the region we shade (Figure 6.4.8).
How to: Given an inequality bounded by a parabola, sketch a graph
- Graph the parabola as if it were an equation. This is the boundary for the region that is the solution set.
- If the boundary is included in the region (the operator is ≤ or ≥), the parabola is graphed as a solid line.
- If the boundary is not included in the region (the operator is < or >), the parabola is graphed as a dashed line.
- Test a point in one of the regions to determine whether it satisfies the inequality statement. If the statement is true, the solution set is the region including the point. If the statement is false, the solution set is the region on the other side of the boundary line.
- Shade the region representing the solution set.
Example 6.4.4: Graphing an Inequality for a Parabola
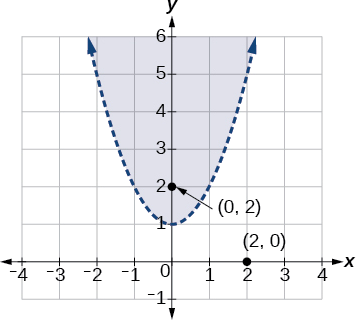
Graph the inequality y>x2+1.
Solution
First, graph the corresponding equation y=x2+1. Since y>x2+1 has a greater than symbol, we draw the graph with a dashed line. Then we choose points to test both inside and outside the parabola. Let’s test the points
(0,2) and (2,0). One point is clearly inside the parabola and the other point is clearly outside.
y>x2+12>(0)2+12>1True0>(2)2+10>5False
The graph is shown in Figure 6.4.9. We can see that the solution set consists of all points inside the parabola, but not on the graph itself.
Graphing a System of Nonlinear Inequalities
Now that we have learned to graph nonlinear inequalities, we can learn how to graph systems of nonlinear inequalities. A system of nonlinear inequalities is a system of two or more inequalities in two or more variables containing at least one inequality that is not linear. Graphing a system of nonlinear inequalities is similar to graphing a system of linear inequalities. The difference is that our graph may result in more shaded regions that represent a solution than we find in a system of linear inequalities. The solution to a nonlinear system of inequalities is the region of the graph where the shaded regions of the graph of each inequality overlap, or where the regions intersect, called the feasible region.
How to: Given a system of nonlinear inequalities, sketch a graph
- Find the intersection points by solving the corresponding system of nonlinear equations.
- Graph the nonlinear equations.
- Find the shaded regions of each inequality.
- Identify the feasible region as the intersection of the shaded regions of each inequality or the set of points common to each inequality.
Example 6.4.5: Graphing a System of Inequalities
Graph the given system of inequalities.
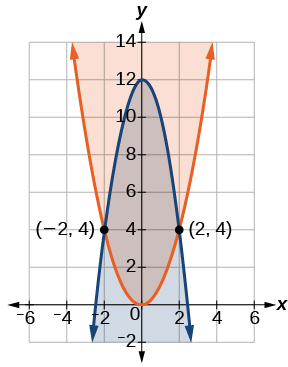
x2−y≤02x2+y≤12
Solution
These two equations are clearly parabolas. We can find the points of intersection by the elimination process: Add both equations and the variable y will be eliminated. Then we solve for x.
x2−y=02x2+y=12_3x2=12x2=4x=±2
Substitute the x-values into one of the equations and solve for y.
x2−y=0(2)2−y=04−y=0y=4(−2)2−y=04−y=0y=4
The two points of intersection are (2,4) and (−2,4). Notice that the equations can be rewritten as follows.
x2−y≤0x2≤yy≥x22x2+y≤12y≤−2x2+12
Graph each inequality. See Figure 6.4.10. The feasible region is the region between the two equations bounded by 2x2+y≤12 on the top and x2−y≤0 on the bottom.
Exercise 6.4.5
Graph the given system of inequalities.
y≥x2−1x−y≥−1
- Answer
-
Shade the area bounded by the two curves, above the quadratic and below the line.
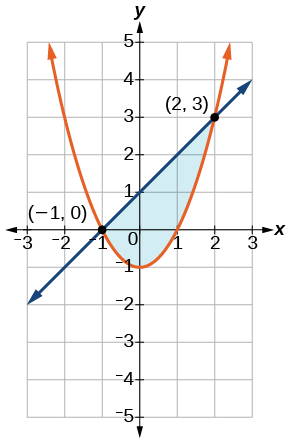
Figure 6.4.11
Media
Access these online resources for additional instruction and practice with nonlinear equations.
Key Concepts
- There are three possible types of solutions to a system of equations representing a line and a parabola: (1) no solution, the line does not intersect the parabola; (2) one solution, the line is tangent to the parabola; and (3) two solutions, the line intersects the parabola in two points. See Example 6.4.1.
- There are three possible types of solutions to a system of equations representing a circle and a line: (1) no solution, the line does not intersect the circle; (2) one solution, the line is tangent to the parabola; (3) two solutions, the line intersects the circle in two points. See Example 6.4.2.
- There are five possible types of solutions to the system of nonlinear equations representing an ellipse and a circle:
(1) no solution, the circle and the ellipse do not intersect; (2) one solution, the circle and the ellipse are tangent to each other; (3) two solutions, the circle and the ellipse intersect in two points; (4) three solutions, the circle and ellipse intersect in three places; (5) four solutions, the circle and the ellipse intersect in four points. See Example 6.4.3. - An inequality is graphed in much the same way as an equation, except for > or <, we draw a dashed line and shade the region containing the solution set. See Example 6.4.4.
- Inequalities are solved the same way as equalities, but solutions to systems of inequalities must satisfy both inequalities. See Example 6.4.5.
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


