2.E: Vector-Valued Functions (Exercises)

2.2: Vector-Valued Functions and Space Curves

1) Given \(\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}\), find the following values (if possible).

a. \(\mathrm{r(\frac{\pi}{4})}\)

b. \(\mathrm{r(\pi)}\)

c. \(\mathrm{r(\frac{\pi}{2})}\)

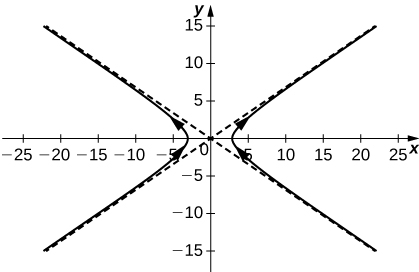
2) Sketch the curve of the vector-valued function \(\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}\) and give the orientation of the curve. Sketch asymptotes as a guide to the graph.

Answer:

3. Evaluate \(\mathrm{\lim \limits_{t \to 0}⟨e^t \mathbf{i}+\frac{\sin t}{t} \mathbf{j}+e^{−t} \mathbf{k}⟩}\)

4. Given the vector-valued function \(\mathrm{r(t)=⟨\cos t,\sin t⟩}\) find the following values:

a. \(\mathrm{\lim \limits_{t \to \frac{\pi}{4}} r(t)}\)

b. \(\mathrm{r(\frac{\pi}{3})}\)

c. Is \(\mathrm{r(t)}\) continuous at \(\mathrm{t=\frac{\pi}{3}}\)? Explain.

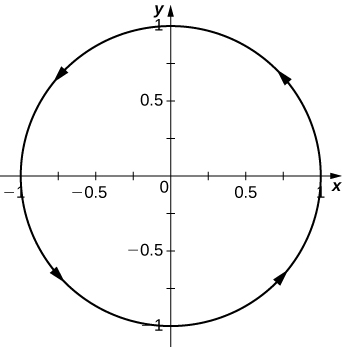
d. Graph \(\mathrm{r(t)}\).

Answer: a. \(\mathrm{⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}}\)⟩, b. ⟨\(\mathrm{\frac{1}{2},\frac{\sqrt{3}}{2}}\)⟩, c. Yes, the limit as t approaches \(\mathrm{\frac{\pi}{3}}\) is equal to \(\mathrm{r(\frac{\pi}{3})}\), d.

5) Given the vector-valued function \(\mathrm{r(t)=⟨t,t^2+1⟩}\), find the following values:

a. \(\mathrm{\lim \limits_{t \to -3} r(t)}\)

b. \(\mathrm{r(−3)}\)

c. Is \(\mathrm{r(t)}\) continuous at \(\mathrm{x=−3}\)?

d. \(\mathrm{r(t+2)−r(t)}\)

6) Let \(\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}\). Find the following values:

a. \(\mathrm{r(\frac{\pi}{4})}\)

b. \(\mathrm{\lim \limits_{t \to \frac{\pi}{4} } r(t)}\)

c. Is \(\mathrm{r(t)}\) continuous at \(\mathrm{t=\frac{\pi}{4}}\)? Explain.

Answer: a. ⟨\(\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}\)⟩; b. ⟨\(\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}\)⟩; c. Yes

Find the limit of the following vector-valued functions at the indicated value of t.

7. \(\mathrm{\lim \limits_{t \to 4}⟨\sqrt{t−3},\frac{\sqrt{t}−2}{t−4},\tan(\frac{\pi}{t})⟩}\)

8. \(\mathrm{\lim \limits_{t \to \frac{\pi}{2}} r(t)}\) for \(\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}\)

Answer: \(\mathrm{⟨e^{\frac{\pi}{2}},1,\ln(\frac{\pi}{2})⟩}\)

9) \(\mathrm{\lim \limits_{t \to \infty}⟨e^{−2t},\frac{2t+3}{3t−1},\arctan(2t)⟩}\)

10) \(\mathrm{\lim \limits_{t \to e^2}⟨t \ln (t),\frac{\ln t}{t^2},\sqrt{\ln(t^2)⟩}}\)

Answer: \(\mathrm{2e^2 \mathbf{i}+\frac{2}{e^4}\mathbf{j}+2\mathbf{k}}\)

11) \(\mathrm{\lim \limits_{t \to \frac{\pi}{6}}⟨\cos 2t,\sin 2t,1⟩}\)

12) \(\mathrm{\lim \limits_{t \to \infty} r(t)}\) for \(\mathrm{r(t)=2e^{−t} \mathbf{ i}+e^{−t} \mathbf{j}+\ln(t−1) \mathbf{k}}\)

Answer: The limit does not exist because the limit of \(\mathrm{\ln(t−1)}\) as t approaches infinity does not exist.

13) Describe the curve defined by the vector-valued function \(\mathrm{r(t)=(1+t)\mathbf{i}+(2+5t)\mathbf{j}+(−1+6t)\mathbf{k}}\).

Find the domain of the vector-valued functions.

14)  \(\mathrm{r(t)=⟨t^2,\tan t,\ln t⟩}\)

Answer: \(\mathrm{t>0,t≠(2k+1)\frac{\pi}{2}}\), where k is an integer

15)  \(\mathrm{r(t)=⟨t^2,\sqrt{t−3},\frac{3}{2t+1}⟩}\)

16)  \(\mathrm{r(t)=⟨\csc(t),\frac{1}{\sqrt{t−3}}, \ln(t−2)⟩}\)

Answer: \(\mathrm{t>3,t≠n\pi}\), where n is an integer

17) Let \(\mathrm{r(t)=⟨\cos t,t,\sin t⟩}\) 

a. For what values of t is \(\mathrm{r(t)}\) continuous?

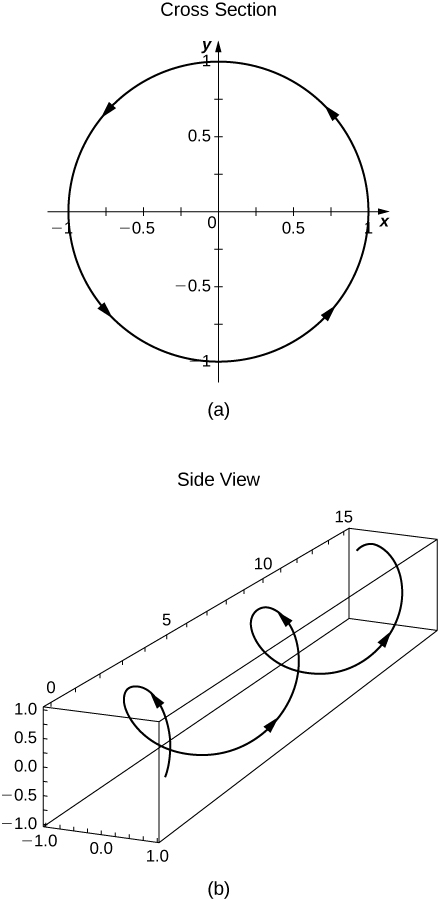
b. Sketch the graph of \(\mathrm{r(t)}\).

Answer:

Note: The cross section is in xz-plane, not in xy-plane

18) Let \(\mathrm{r(t)=2e^{-t} \mathbf{i}+e^{−t}\mathbf{j}+\ln(t−1)\mathbf{k}}\).

a. Find the domain of \(\mathrm{r(t)}\)

b. For what values of t is \(\mathrm{r(t)}\) continuous?

Answer: All t such that \(\mathrm{t∈(1,\infty)}\)

19) Eliminate the parameter t, write the equation in Cartesian coordinates, then sketch the graphs of the vector-valued functions. 

a. \(\mathrm{r(t)=2t\mathbf{i}+t^2 \mathbf{j}}\)

b. \(\mathrm{r(t)=t^3 \mathbf{i}+2t \mathbf{j}}\) 

c. \(\mathrm{r(t)=2(\sinh t)\mathbf{i}+2(\cosh t) \mathbf{j},t>0}\)

d. \(\mathrm{r(t)=3(cost)i+3(sint)j}\) 

20) Use a graphing utility to sketch each of the following vector-valued functions:

a. \(\mathrm{r(t)=2 \cos t^2 \mathbf{i}+(2−\sqrt{t})\mathbf{j}}\) 

b. \(\mathrm{r(t)=⟨e^{\cos (3t)},e^{−\sin(t)}⟩}\)

c. \(\mathrm{r(t)=⟨2−\sin (2t),3+2 \cos t⟩}\) 

21) Find a vector-valued function that traces out the given curve in the indicated direction. Sketch the graphs of each curve.

a. \(\mathrm{4x^2+9y^2=36}\); clockwise and counterclockwise

b. \(\mathrm{y=x^2}\); from left to right  

c. The line through P and Q where P is \(\mathrm{(1,4,−2)}\) and Q is \(\mathrm{(3,9,6)}\)

d. The circle \(\mathrm{x^2+y^2=36}\), oriented clockwise, with position \(\mathrm{(6,0)}\) at time \(\mathrm{t=0}\).

e. The ellipse \(\mathrm{x^2+\frac{y^2}{36}=1}\) oriented counterclockwise

f. The hyperbola \(\mathrm{\frac{y^2}{36}-x^2=1}\)  top piece is oriented from left-to-right

g. The hyperbola \(\mathrm{\frac{x^2}{49}-\frac{y^2}{64}=1}\)  right piece is oriented from bottom-to-top

22) Consider the curve described by the vector-valued function \(\mathrm{r(t)=(50e^{−t}\cos t)\mathbf{i}+(50e^{−t}\sin t)\mathbf{j}+(5−5e^{−t})\mathbf{k}}\).

a. What is the initial point of the path corresponding to \(\mathrm{r(0)}\)? 

b. What is \(\mathrm{\lim \limits_{t \to \infty}r(t)} \)? 

c. Eliminate the parameter t to show that \(\mathrm{z=5−\frac{u}{10}}\) where \(\mathrm{u^2=x^2+y^2}\).

 

2.3: Calculus of Vector-Valued Functions

1) Compute the derivatives of the vector-valued functions.

\(\mathrm{r(t)=t^3 \mathbf{i}+3t^2 \mathbf{j}+\frac{t^3}{6}\mathbf{k}}\)

Answer: \(\mathrm{r'(t)=⟨3t^2,6t,\frac{1}{2}t^2⟩}\)

2) \(\mathrm{r(t)=\sin(t) \mathbf{i}+\cos(t) \mathbf{j}+e^t \mathbf{k}}\)

3) \(\mathrm{r(t)=e^{−t} \mathbf{i}+\sin(3t) \mathbf{j}+10 \sqrt{t} \mathbf{k}}\). A sketch of the graph is shown here. Notice the varying periodic nature of the graph.

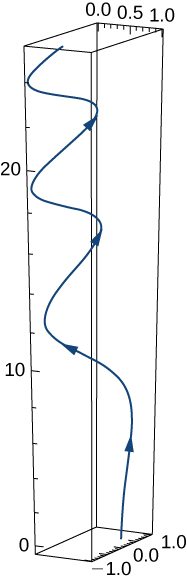
Answer: \(\mathrm{r'(t)=⟨−e^{−t},3\cos (3t),\frac{5}{\sqrt{t}}⟩}\)

4) \(\mathrm{r(t)=e^t \mathbf{i}+2e^t \mathbf{j}+\mathbf{k}}\)

5) \(\mathrm{r(t)=\mathbf{i}+\mathbf{j}+\mathbf{k}}\)

Answer: \(\mathrm{r'(t)=⟨0,0,0⟩}\)

6) \(\mathrm{r(t)=te^t \mathbf{i}+t \ln(t) \mathbf{j}+\sin(3t)\mathbf{k}}\)

7) \(\mathrm{r(t)=\frac{1}{t+1} \mathbf{i}+\arctan(t) \mathbf{j}+\ln t^3 \mathbf{k}}\)

Answer: \(\mathrm{r'(t)=⟨\frac{−1}{(t+1)^2},\frac{1}{1+t^2},\frac{3}{t}⟩}\)

8) \(\mathrm{r(t)= \tan(2t) \mathbf{i}+\sec(2t) \mathbf{j}+\sin ^2 (t) \mathbf{k}}\)

9) \(\mathrm{r(t)=3 \mathbf{i}+4 \sin (3t) \mathbf{j}+ t \cos(t) \mathbf{k}}\)

Answer:\(\mathrm{r'(t)=⟨0,12 \cos(3t), \cos t−t \sin t⟩}\)

10) \(\mathrm{r(t)=t^2 \mathbf{i}+te^{−2t} \mathbf{j}−5e^{−4t} \mathbf{k}}\)

For the following problems, find a tangent vector at the indicated value of t.

11) \(\mathrm{r(t)=t \mathbf{i}+\sin(2t) \mathbf{j}+\cos(3t) \mathbf{k}}\); \(\mathrm{t=\frac{π}{3}}\)

Answer: \(\mathrm{\frac{1}{\sqrt{2}}⟨1,−1,0⟩}\)

12) \(\mathrm{r(t)=3t^3 \mathbf{i}+2t^2 \mathbf{j}+\frac{1}{t} \mathbf{k};t=1}\)

13) \(\mathrm{r(t)=3e^t \mathbf{i}+2e^{−3t} \mathbf{j}+4e^{2t} \mathbf{k}; t= \ln(2)}\)

 Answer: \(\mathrm{\frac{1}{\sqrt{1060.5625}}⟨6,−\frac{3}{4},32⟩}\)

14) \(\mathrm{r(t)=\cos(2t) \mathbf{i}+2 \sin t \mathbf{j}+t^2 \mathbf{k};t=\frac{π}{2}}\)

Find the unit tangent vector for the following parameterized curves.

15) \(\mathrm{r(t)=6 \mathbf{i}+\cos(3t) \mathbf{j}+3\sin(4t) \mathbf{k}, 0≤t<2π}\)

Answer: \(\mathrm{\frac{1}{\sqrt{9sin ^2 (3t)+144\cos ^2 (4t)}}⟨0,−3\sin(3t),12\cos(4t)⟩}\)

16) \(\mathrm{r(t)=\cos t \mathbf{i}+\sin t \mathbf{j}+\sin t \mathbf{k}, 0≤t<2π}\). Two views of this curve are presented here:

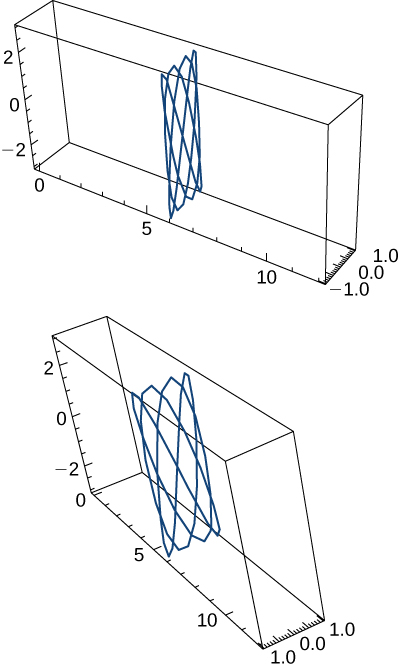
17) \(\mathrm{r(t)=3 \cos(4t) \mathbf{i}+3 \sin(4t) \mathbf{j}+5t \mathbf{k},1≤t≤2}\)

Answer: \(\mathrm{T(t)=−\frac{12}{13} \sin(4t) \mathbf{i}+ \frac{12}{13}\cos (4t) \mathbf{j}+\frac{5}{13} \mathbf{k}}\)

18) \(\mathrm{r(t)=t \mathbf{i}+3t \mathbf{j}+t^2 \mathbf{k}}\)

19) Let \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}−t^4 \mathbf{k}}\) and \(\mathrm{s(t)=\sin(t) \mathbf{i}+e^t \mathbf{j}+ \cos(t) \mathbf{k}}\) 

Find the following.

a. \(\mathrm{\frac{d}{dt}[r(t^2)]}\) 

b. \(\mathrm{\frac{d}{dt}[(t^2)s(t)]}\)

c. \(\mathrm{\frac{d}{dt}[r(t)⋅s(t)]}\)  

20) Compute the first, second, and third derivatives of \(\mathrm{r(t)=3t \mathbf{i}+6\ln(t) \mathbf{j}+5e^{−3t}\mathbf{k}}\).

21) Find \(\mathrm{r'(t)⋅r''(t) \; for \; r(t)=−3t^5 \mathbf{i}+5t \mathbf{j}+2t^2 \mathbf{k}.}\)

Answer: \(\mathrm{900t^7+16t}\)

22) Evaluate \(\mathrm{\frac{d}{dt}[u(t) \times u′(t)]}\) given \(\mathrm{u(t)=t^2 \mathbf{i}−2t \mathbf{j}+\mathbf{k}}\).

Answer: \(\mathrm{0 \mathbf{i} +2 \mathbf{j}+4t \mathbf{j}}\)

23) Find the antiderivative of \(\mathrm{r'(t)=\cos(2t) \mathbf{i}−2\sin t \mathbf{j}+\frac{1}{1+t^2} \mathbf{k}}\) that satisfies the initial condition \(\mathrm{r(0)=3 \mathbf{i}−2 \mathbf{j}+\mathbf{k}}\).

24) Evaluate \(\mathrm{\int_0^3‖ti+t^2j‖dt}\).

Answer: \(\mathrm{\frac{1}{3}(10^{\frac{3}{2}}−1)}\)

25) Given \(\mathrm{r(t)=t \mathbf{i}+3t \mathbf{j}+t^2 \mathbf{k}}\) and \(\mathrm{u(t)=4t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k}}\), find \(\mathrm{\frac{d}{dt}(r(t) \times u(t))}\).

26) Find an equation of the tangent line to the curve \(\mathrm{r(t)=⟨e^t,e^{−t},0⟩}\) at \(\mathrm{t=0}\).

Answer: \(\mathrm{x−1=t,y−1=−t,z−0=0}\)

27) Let \(\mathrm{r(t)=⟨6t,6t−t^2⟩}\). 

a. Describe and sketch the curve represented by the vector-valued function \(\mathrm{r(t)}\)

b. Locate the highest point on the curve \(\mathrm{r(t)=⟨6t,6t−t^2⟩}\) and give the value of the function at this point.

Answer: \(\mathrm{r(t)=⟨18,9⟩}\) at \(\mathrm{t=3}\)

28) Find the unit tangent vector T(t) for the following vector-valued functions.

a. \(\mathrm{r(t)=⟨t,\frac{1}{t}⟩}\). The graph is shown here:

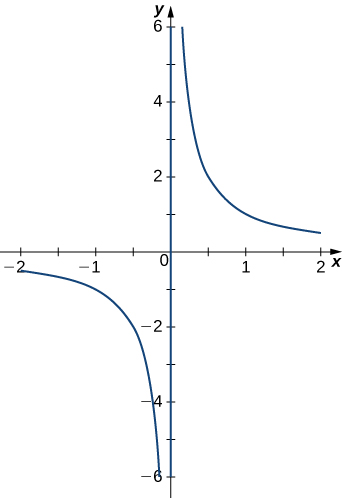
Answer: \(\mathrm{T(t)=⟨\frac{t^2}{\sqrt{t^4+1}},\frac{-1}{\sqrt{t^4+1}}⟩}\)

b. \(\mathrm{r(t)=⟨t \cos t,t sin t⟩}\)

c. \(\mathrm{r(t)=⟨t+1,2t+1,2t+2⟩}\)

Answer: \(\mathrm{T(t)=\frac{1}{3} ⟨1,2,2⟩}\)

29) Evaluate the following integrals:

a. \(\mathrm{\int (e^t \mathbf{i}+\sin t \mathbf{j}+ \frac{1}{2t−1} \mathbf{k})dt}\)

b. \(\mathrm{\int_0^1 r(t)dt}\), where \(\mathrm{r(t)=⟨\sqrt[3]{t},\frac{1}{t+1},e^{−t}⟩}\)

Answer:\(\mathrm{\frac{3}{4}\mathbf{i}+\ln(2) \mathbf{j}+(1−\frac{1}{e}) \mathbf{k}}\)

30) For each of the following vector valued functions determine any values of t at which \(\mathrm{r(t)=\mathbf{r}(t)}\)  is not smooth. Determine the open intervals on which \(\mathrm{r(t)=\mathbf{r}(t)}\) is smooth. 

a. \(\vecs r(t) = \langle 3t, 5t^2 - 1\rangle\)

b. \(\vecs r(t)= t^3\,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}\) 

Answer:

\(\vecs r\) is not smooth at \(t = 0\), since \(\vecs r'(0) = \vecs 0\).
\(\vecs r\) is smooth on the open intervals \((-\infty, 0)\) and \((0, \infty)\).

c. \(\vecs r(t)=\langle 5,\, 2 \sin (t),\, \cos(t)\rangle\)

d. \(\vecs r(t) = \langle t^3 - 3t^2, 7\rangle\)

Answer:

\(\vecs r\) is not smooth at \(t = 0\) and \(t = 2\), since \(\vecs r'(0) = \vecs 0\) and \(\vecs r'(2) = \vecs 0\).
\(\vecs r\) is smooth on the open intervals \((-\infty, 0)\), \((0, 2)\), and \((2, \infty)\).

e. \(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+t^3 \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}\)

f. \(\vecs r(t)=\left\langle \ln(t^2+4t+5), \,\dfrac{t^3}{3} - 4t,\, 5\right\rangle\)

Answer:

\(\vecs r\) is not smooth at \(t = -2\), since \(\vecs r'(-2) = \vecs 0\).
Since the domain of \(\vecs r\) is \((-\infty, \infty)\), this is all we have to remove.
\(\vecs r\) is smooth on the open intervals \((-\infty, -2)\) and \((-2, \infty)\).

g. \(\vecs r(t) = \left( 5\cos t - \cos 5t\right) \,\hat{\mathbf{i}} + \left( 5\sin t - \sin 5t \right) \,\hat{\mathbf{j}}\), for \(0 \le t \le 2\pi\)

h. \(\vecs r(t)=\sqrt{t^3 + 9t^2} \,\hat{\mathbf{i}}+\left(t^2 +12t\right) \,\hat{\mathbf{j}}+7\,\hat{\mathbf{k}}\)

Answer:

The domain of \(\vecs r\) is \([-9, \infty)\). And \(\vecs r\) is not smooth at \(t = -6\), since \(\vecs r'(-6) = \vecs 0\).
The domain of \(\vecs r'\) is \((-9, \infty)\), since \(\vecs r'\) is undefined at \(t = -9\).
\(\vecs r\) is smooth on the open intervals \((-9, -6)\) and \((-6, \infty)\).

i. \(\vecs r(t)= \cos^3 t\,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}\), for \(0 \le t \le 2\pi\)

Answer:

The domain of \(\vecs r\) is \((-\infty, \infty)\).
\(\vecs r'(t) = -3(\cos^2 t)(\sin t)\,\hat{\mathbf{i}}+\cos t \,\hat{\mathbf{j}}\). It's domain is also \((-\infty, \infty)\).
But note that both components have a factor of \(\cos t\), so both components will be \(0\) when \(\cos t = 0\).
Therefore, \(\vecs r\) is not smooth at \(t = \frac{\pi}{2}\) and at \(t = \frac{3\pi}{2}\), since \(\vecs r'\left( \frac{\pi}{2}\right) = \vecs 0\) and \(\vecs r'\left( \frac{3\pi}{2}\right) = \vecs 0\). Note then that \(\vecs r\) is not smooth for any odd multiple of \(\frac{\pi}{2}\), that is for \(t = \frac{(2n + 1)\pi}{2}\), for any integer value \(n\).
\(\vecs r\) is smooth on the open intervals \(\left(\dfrac{(2n - 1)\pi}{2}, \dfrac{(2n + 1)\pi}{2}\right)\), for any integer value \(n\).
 

2.4: Arc Length and Curvature

Exercises

1) Find the arc length of the curve on the given interval.

a. \(\mathrm{r(t)=t^2 \mathbf{i}+14t \mathbf{j},0≤t≤7}\). This portion of the graph is shown here:

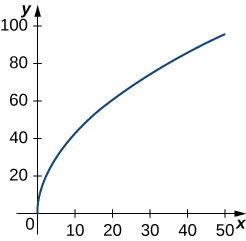
b. \(\mathrm{r(t)=t^2 \mathbf{i}+(2t^2+1)\mathbf{j},1≤t≤3}\)

Answer: \(\mathrm{8\sqrt{5}}\)

c. \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩,0≤t≤π}\). This portion of the graph is shown here:

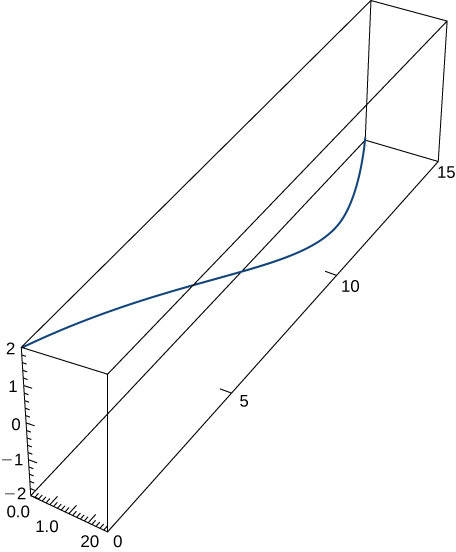
d. \(\mathrm{r(t)=⟨t^2+1,4t^3+3⟩,−1≤t≤0}\)

Answer: \(\mathrm{\frac{1}{54}(37^{3/2}−1)}\)

e. \(\mathrm{r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩}\) over the interval \(\mathrm{[0,\frac{π}{2}]}\). Here is the portion of the graph on the indicated interval:

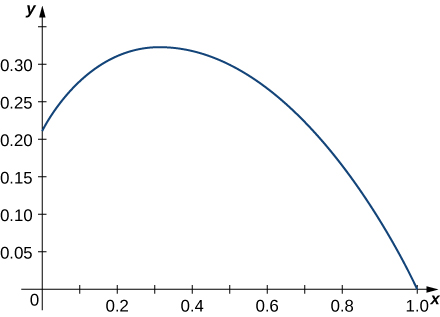
2) Find the length of one turn of the helix given by \(\mathrm{r(t)= \frac{1}{2} \cos t \mathbf{i}+\frac{1}{2} \sin t \mathbf{j}+\sqrt{\frac{3}{4}}t \mathbf{k}.}\)

Answer: Length \(\mathrm{=2π}\)

3) Find the arc length of the vector-valued function \(\mathrm{r(t)=−t \mathbf{i}+4t \mathbf{j}+3t \mathbf{k}}\) over \(\mathrm{[0,1]}\).

4) A particle travels in a circle with the equation of motion \(\mathrm{r(t)=3 \cos t \mathbf{i}+3 \sin t \mathbf{j} +0 \mathbf{k}}\). Find the distance traveled around the circle by the particle.

Answer: \(\mathrm{6π}\)

5) Set up an integral to find the circumference of the ellipse with the equation \(\mathrm{r(t)= \cos t \mathbf{i}+2 \sin t \mathbf{j}+0\mathbf{k}.}\)

6) Find the length of the curve \(\mathrm{r(t)=⟨\sqrt{2}t,e^t,e^{−t}⟩}\) over the interval \(\mathrm{0≤t≤1}\). The graph is shown here:

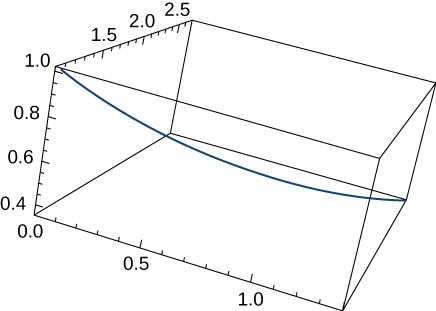
Answer: \(\mathrm{e−\frac{1}{e}}\)

7) Find the length of the curve \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\) for \(\mathrm{t∈[−10,10]}\).

8) The position function for a particle is \(\mathrm{r(t)=a \cos( ωt) \mathbf{i}+b \sin (ωt) \mathbf{j}}\). Find the unit tangent vector, the unit normal vector and the binormal vector at \(\mathrm{t=0.}\)

Answer: \(\mathrm{T(0)= \mathbf{j}, N(0)=−\mathbf{i}, B(0)=\mathbf{k}}\)

9) Given \(\mathrm{r(t)=a \cos (ωt) \mathbf{i} +b \sin (ωt) \mathbf{j}}\), find the binormal vector \(\mathrm{B(0)}\).

10) Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), determine the tangent vector \(\mathrm{T(t)}\).

Answer: \(\mathrm{T(t)=⟨2e^t,e^t \cos t−e^t \sin t,e^t \cos t+e^t \sin t⟩}\)

11) Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), determine the unit tangent vector \(\mathrm{T(t)}\) evaluated at \(\mathrm{t=0}\).

12) Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), find the unit tangent vector, the unit normal vector, and the binormal vector evaluated at \(\mathrm{t=0}\)

Answer: \(\mathrm{T(0)=⟨\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}}⟩}\),\(\mathrm{N(0)=⟨0,-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩}\), \(\mathrm{B(0)=⟨\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}⟩}\)

13) Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), find the unit normal vector evaluated at \(\mathrm{t=0}\).

14) Given \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}+t\mathbf{k}}\), find the unit tangent vector \(\mathrm{T(t)}\). The graph is shown here:

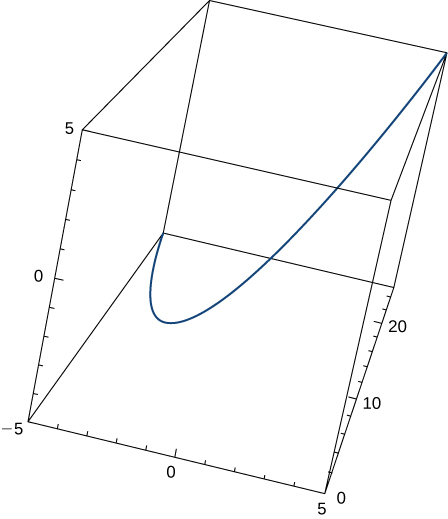
Answer: \(\mathrm{T(t)=\frac{1}{\sqrt{4t^2+2}}<1,2t,1>}\)

15) Find the unit tangent vector \(\mathrm{T(t)}\) and unit normal vector \(\mathrm{N(t)}\) at \(\mathrm{t=0}\) for the plane curve \(\mathrm{r(t)=⟨t^3−4t,5t^2−2⟩}\). The graph is shown here:

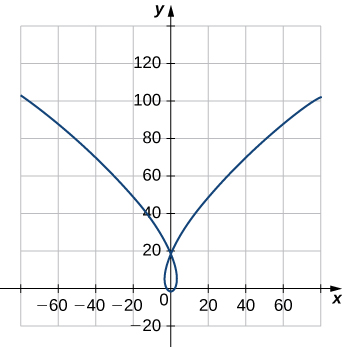
16) Find the unit tangent vector \(\mathrm{T(t)}\) for \(\mathrm{r(t)=3t \mathbf{i}+5t^2 \mathbf{j}+2t\mathbf{k}}\)

Answer: \(\mathrm{T(t)=\frac{1}{\sqrt{100t^2+13}}(3\mathbf{i}+10t\mathbf{j}+2\mathbf{k})}\)

17) Find the principal normal vector to the curve \(\mathrm{r(t)=⟨6 \cos t,6 \sin t⟩}\) at the point determined by \(\mathrm{t=π/3}\).

18) Find \(\mathrm{T(t)}\) for the curve \(\mathrm{r(t)=(t^3−4t) \mathbf{i}+(5t^2−2)\mathbf{j}}\).

Answer: \(\mathrm{T(t)=\frac{1}{\sqrt{9t^4+76t^2+16}}([3t^2−4]\mathbf{i}+10t\mathbf{j})}\)

19) Find \(\mathrm{N(t)}\) for the curve \(\mathrm{r(t)=(t^3−4t)\mathbf{i}+(5t^2−2)\mathbf{j}}\).

20) Find the unit normal vector \(\mathrm{N(t)}\) for \(\mathrm{r(t)=⟨2sint,5t,2cost⟩}\).

Answer: \(\mathrm{N(t)=⟨−sint,0,−cost⟩}\)

21) Find the unit tangent vector \(\mathrm{T(t)}\) for \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\).

22) Find the arc-length function \(\mathrm{s(t)}\) for the line segment given by \(\mathrm{r(t)=⟨3−3t,4t⟩}\). Write r as a parameter of s.

Answer: Arc-length function: \(\mathrm{s(t)=5t}\); r as a parameter of s: \(\mathrm{r(s)=(3−\frac{3s}{5})\mathbf{i}+\frac{4s}{5}\mathbf{j}}\)

23) Parameterize the helix \(\mathrm{r(t)= \cos t \mathbf{i}+ \sin t \mathbf{j}+t \mathbf{k}}\) using the arc-length parameter s, from \(\mathrm{t=0}\).

24) Parameterize the curve using the arc-length parameter s, at the point at which \(\mathrm{t=0}\) for \(\mathrm{r(t)=e^t \sin t \mathbf{i} + e^t \cos t \mathbf{j}}\)

Answer: \(\mathrm{(s)=(1+\frac{s}{\sqrt{2}}) \sin ( \ln (1+ \frac{s}{\sqrt{2}})) \mathbf{i} +(1+ \frac{s}{\sqrt{2}}) \cos [ \ln (1+\frac{s}{\sqrt{2}})]\mathbf{j}}\)

25) Find the curvature of the curve \(\mathrm{r(t)=5 \cos t \mathbf{i}+4 \sin t \mathbf{j}}\) at \(\mathrm{t=π/3}\). (Note: The graph is an ellipse.)

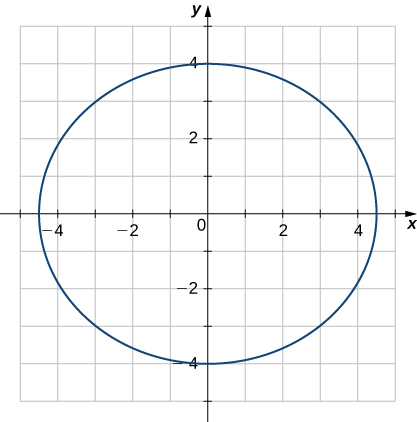
26) Find the x-coordinate at which the curvature of the curve \(\mathrm{y=1/x}\) is a maximum value.

Answer: The maximum value of the curvature occurs at \(\mathrm{x=\pm1}\).

27) Find the curvature of the curve \(\mathrm{r(t)=5 \cos t \mathbf{i}+5 \sin t \mathbf{j}}\). Does the curvature depend upon the parameter t?

28) Find the curvature \(κ\) for the curve \(\mathrm{y=x−\frac{1}{4}x^2}\) at the point \(\mathrm{x=2}\).

Answer:  \(\mathrm{\frac{1}{2}}\)

29) Find the curvature \(κ\) for the curve \(\mathrm{y=\frac{1}{3}x^3}\) at the point \(\mathrm{x=1}\).

30) Find the curvature κκ of the curve \(\mathrm{r(t)=t \mathbf{i}+6t^2 \mathbf{j}+4t \mathbf{k}}\). The graph is shown here:

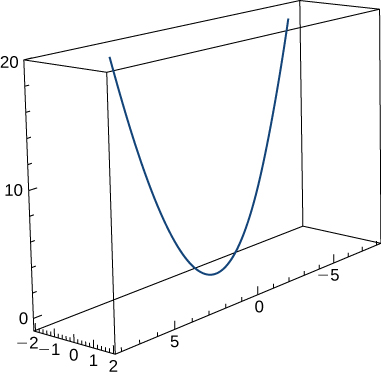
Answer: \(\mathrm{κ≈\frac{49.477}{(17+144t^2)^{3/2}}}\)

31) Find the curvature of \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\).

32) Find the curvature of \(\mathrm{r(t)=\sqrt{2}t \mathbf{i}+e^t \mathbf{j}+e^{−t} \mathbf{k}}\) at point \(\mathrm{P(0,1,1)}\).

Answer: \(\mathrm{\frac{1}{2\sqrt{2}}}\)

33) At what point does the curve \(\mathrm{y=e^x}\) have maximum curvature? What happens to the curvature as \(\mathrm{x→∞}\) for the curve \(\mathrm{y=e^x}\)? 

34) Find the point of maximum curvature on the curve \(\mathrm{y=\ln x}\).

35) Find the equations of the normal plane and the osculating plane of the curve \(\mathrm{r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩}\) at point \(\mathrm{(0,π,−2)}\).

Answer: \(\mathrm{y=6x+π}\) and \(\mathrm{x+6y=6π}\)

36) Find equations of the osculating circles of the ellipse \(\mathrm{4y^2+9x^2=36}\) at the points \(\mathrm{(2,0)}\) and \(\mathrm{(0,3)}\).

37) Find the equation for the osculating plane at point \(\mathrm{t=π/4}\) on the curve \(\mathrm{r(t)=\cos (2t) \mathbf{i}+ \sin (2t) \mathbf{j}+t}\).

Answer: (\mathrm{x+2z=\frac{π}{2}}\)

38) Find the radius of curvature of \(\mathrm{6y=x^3}\) at the point \(\mathrm{(2,\frac{4}{3}).}\)

39) Find the curvature at each point \(\mathrm{(x,y)}\) on the hyperbola \(\mathrm{r(t)=⟨a \cosh( t),b \sinh (t)⟩}\).

Answer: \(\mathrm{\frac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}}\)

40) Calculate the curvature of the circular helix \(\mathrm{r(t)=r \sin (t) \mathbf{i}+r \cos (t) \mathbf{j}+t \mathbf{k}}\).

41) Find the radius of curvature of \(\mathrm{y= \ln (x+1)}\) at point \(\mathrm{(2,\ln 3)}\).

Answer: \(\mathrm{\frac{10\sqrt{10}}{3}}\)

42) Find the radius of curvature of the hyperbola \(\mathrm{xy=1}\) at point \(\mathrm{(1,1)}\).

43) A particle moves along the plane curve C described by \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}}\). Solve the following problems.

a. Find the length of the curve over the interval \(\mathrm{[0,2]}\). 

b. Find the curvature of the plane curve at \(\mathrm{t=0,1,2}\).

c. Describe the curvature as t increases from \(\mathrm{t=0}\) to \(\mathrm{t=2}\). 

 

2.5: Motion in Space

1) Given \(\vecs r(t)=(3t^2−2)\,\hat{\mathbf{i}}+(2t−\sin t)\,\hat{\mathbf{j}}\),

a. find the velocity of a particle moving along this curve.

b. find the acceleration of a particle moving along this curve.

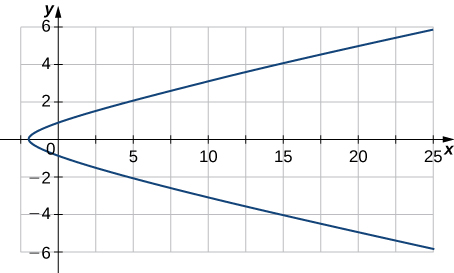
Answer: a. \(\vecs v(t)=6t\,\hat{\mathbf{i}}+(2−\cos t)\,\hat{\mathbf{i}}\); b. \(\vecs a(t)=6\,\hat{\mathbf{i}}+\sin t\,\hat{\mathbf{i}}\)

2)  Given the position function, find the velocity, acceleration, and speed in terms of the parameter \(t\).

a. \(\vecs r(t)=e^{−t}\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+\tan t\,\hat{\mathbf{k}}\)

b. \(\vecs r(t)=⟨3\cos t,\,3\sin t,\,t^2⟩\)

Answer:

\(\vecs v(t)=-3\sin t\,\hat{\mathbf{i}}+3\cos t\,\hat{\mathbf{j}}+2t\,\hat{\mathbf{k}}\)
\(\vecs a(t)=-3\cos t\,\hat{\mathbf{i}}-3\sin t\,\hat{\mathbf{j}}+2\,\hat{\mathbf{k}}\)
\(\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{9 + 4t^2}\)

c. \(\vecs r(t)=t^5\,\hat{\mathbf{i}}+(3t^2+2t- 5)\,\hat{\mathbf{j}}+(3t-1)\,\hat{\mathbf{k}}\)

d. \(\vecs r(t)=2\cos t\,\hat{\mathbf{j}}+3\sin t\,\hat{\mathbf{k}}\).

Answer:

\(\vecs v(t)=-2\sin t\,\hat{\mathbf{j}}+3\cos t\,\hat{\mathbf{k}}\)
\(\vecs a(t)=-2\cos t\,\hat{\mathbf{j}}-3\sin t\,\hat{\mathbf{k}}\)
\(\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{4\sin^2 t+9\cos^2 t}=\sqrt{4+5\cos^2 t}\)

3) Find the velocity, acceleration, and speed of a particle with the given position function.

a. \(\vecs r(t)=⟨t^2−1,t⟩\)

b. \(\vecs r(t)=⟨e^t,e^{−t}⟩\)

Answer:

\(\vecs v(t)=⟨e^t,−e^{−t}⟩\),
\(\vecs a(t)=⟨e^t, e^{−t}⟩,\)
\( \|\vecs v(t)\| = \sqrt{e^{2t}+e^{−2t}}\)

c. \(\vecs r(t)=⟨\sin t,t,\cos t⟩\). The graph is shown here:

4)  The position function of an object is given by \(\vecs r(t)=⟨t^2,5t,t^2−16t⟩\). At what time is the speed a minimum?

Answer: \(t = 4\)

5) Let \(\vecs r(t)=r\cosh(ωt)\,\hat{\mathbf{i}}+r\sinh(ωt)\,\hat{\mathbf{j}}\). Find the velocity and acceleration vectors and show that the acceleration is proportional to \(\vecs r(t)\).

6) The acceleration function, initial velocity, and initial position of a particle are

\(\mathrm{a(t)=−5 \cos t \mathbf{i}−5\sin t \mathbf{j},v(0)=9 \mathbf{i}+2 \mathbf{j},and \; r(0)=5 \mathbf{i}.}\) Find \(\mathrm{v(t) \; and \; r(t)}\).

7) The position vector of a particle is \(\mathrm{r(t)=5 \sec(2t) \mathrm{i}−4tan(t) \mathrm{j}+7t^2 \mathrm{k}}\). Find the velocity as t approaches but is not equal to \(\mathrm{\frac{π}{4}}\) (if it exists). 

8) Find the velocity and the speed of a particle with the position function \(\mathrm{r(t)=(\frac{2t−1}{2t+1}) \mathbf{i}+\ln(1−4t^2) \mathbf{j}}\). The speed of a particle is the magnitude of the velocity and is represented by \(\mathrm{‖r′(t)‖}\).

9) A particle moves on a circular path of radius b according to the function \(\mathrm{r(t)=b \cos(\omega t) \mathbf{i}+b\sin(\omega) \mathbf{j},}\) where \(\mathrm{\omega}\) is the angular velocity, \(\mathrm{\frac{d \theta}{dt}}\).

a. Find the velocity function and show that \(\mathrm{v(t)}\) is always orthogonal to \(\mathrm{r(t)}\). 

b. Show that the speed of the particle is proportional to the angular velocity.

10) An object starts from rest at point \(\mathrm{P(1,2,0)}\) and moves with an acceleration of\(\mathrm{ a(t)=\mathbf{j}+2 \mathbf{k},}\) where \(\mathrm{‖a(t)‖}\) is measured in feet per second per second. Find the location of the object after \(\mathrm{t=2}\) sec.

11) Given \(\mathrm{r(t)=⟨t+ \cos t,t− \sin t⟩}\), find the velocity and the speed at any time.

Answer: \(\mathrm{v(t)=⟨1− \sin t,1−\cos t⟩, speed =‖v(t)‖ =\sqrt{4−2( \sin t+\cos t)}}\)

12) Find the velocity vector for the function \(\mathrm{r(t)=⟨e^t,e^{−t},0⟩}\).

13) The position vector for a particle is \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k}}\).The graph is shown here:

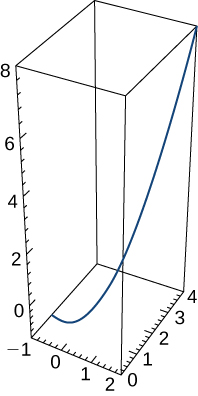
a. Find the velocity vector at any time.

b. Find the speed of the particle at time \(\mathrm{t=2}\) sec.

Answer: \(\mathrm{\sqrt{593}}\)

c. Find the acceleration at time \(\mathrm{t=2}\) sec.

14) A particle travels along the path of a helix with the equation \(\mathrm{r(t)= \cos(t) \mathbf{i}+\sin(t) \mathbf{j}+t \mathbf{k}}\). See the graph presented here:

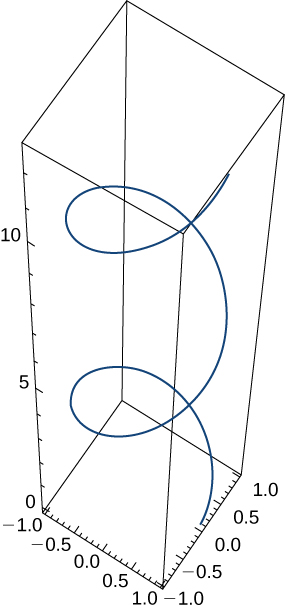
Find the following:

a. Velocity of the particle at any time

b. Speed of the particle at any time

c. Acceleration of the particle at any time

d. Find the unit tangent vector for the helix.

15) A particle travels along the path of an ellipse with the equation \(\mathrm{r(t)=\cos t \mathbf{i}+2 \sin t \mathbf{j}+0 \mathbf{k}}\). Find the following:

a. Velocity of the particle

Answer: \(\mathrm{v(t)=⟨−\sin t,2 \cos t,0⟩}\)

b. Speed of the particle at \(\mathrm{t=\frac{π}{4}}\)

c. Acceleration of the particle at \(\mathrm{t=\frac{π}{4}}\)

Answer:  \(\mathrm{a(t)=⟨−\frac{\sqrt{2}}{2},−\sqrt{2},0⟩}\)

16) Given the vector-valued function \(\mathrm{r(t)=⟨\tan t,\sec t,0⟩}\) (graph is shown here), find the following:

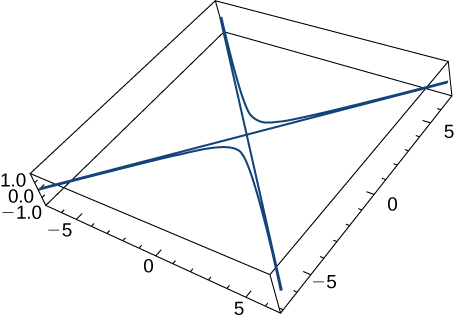
a. Velocity

b. Speed

Answer: \(\mathrm{‖v(t)‖=\sqrt{\sec ^4 t+\sec ^2 t \tan ^2 t}=\sqrt{\sec ^2 t(\sec ^2 t+\tan ^2 t)}}\)

c. Acceleration

17) Find the minimum speed of a particle traveling along the curve \(\mathrm{r(t)=⟨t+\cos t,t−\sin t⟩}\) \(\mathrm{t∈[0,2π)}\).

Answer:  Minimum speed is \(\mathrm{\sqrt{2}-1}\)

18) Consider the motion of a point on the circumference of a rolling circle. As the circle rolls, it generates the cycloid \(\vecs r(t)=(ωt−\sin(ωt))\,\hat{\mathbf{i}}+(1−\cos(ωt))\,\hat{\mathbf{j}}\), where \(\omega\) is the angular velocity of the circle and \(b\) is the radius of the circle:

 

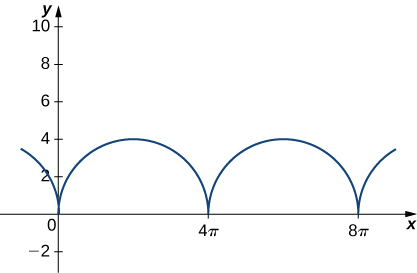
Find the equations for the velocity, acceleration, and speed of the particle at any time.

Answer:

\(\vecs v(t)=(ω−ω\cos(ωt))\,\hat{\mathbf{i}}+(ω\sin(ωt))\,\hat{\mathbf{j}}\)
\(\vecs a(t)=(ω^2\sin(ωt))\,\hat{\mathbf{i}}+(ω^2\cos(ωt))\,\hat{\mathbf{j}}\)
\(\begin{align*} \text{speed}(t) &= \sqrt{(ω−ω\cos(ωt))^2 + (ω\sin(ωt))^2} \\
&= \sqrt{ω^2 - 2ω^2 \cos(ωt) + ω^2\cos^2(ωt) + ω^2\sin^2(ωt)} \\
&= \sqrt{2ω^2(1 - \cos(ωt))} \end{align*} \)

19) A person on a hang glider is spiraling upward as a result of the rapidly rising air on a path having position vector \(\vecs r(t)=(3\cos t)\,\hat{\mathbf{i}}+(3\sin t)\,\hat{\mathbf{j}}+t^2\,\hat{\mathbf{k}}\). The path is similar to that of a helix, although it is not a helix. The graph is shown here:

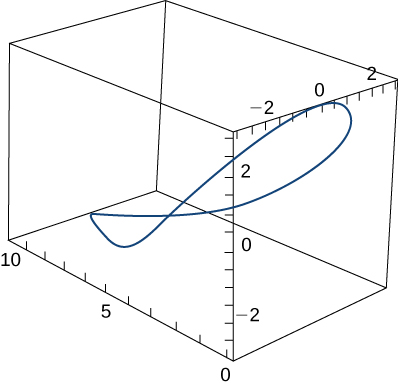
a. Find the velocity and acceleration vectors and the glider’s speed at any time

Answer:  \(\|\vecs v(t)\|=\sqrt{9+4t^2}\)

b. The times, if any, at which the glider’s acceleration is orthogonal to its velocity

20) Given that \(\vecs r(t)=⟨e^{−5t}\sin t,\, e^{−5t}\cos t,\, 4e^{−5t}⟩\) is the position vector of a moving particle, find the velocity, the speed and the acceleration of the particle.

Answer: 

\(\vecs v(t)=⟨e^{−5t}(\cos t−5\sin t),\, −e^{−5t}(\sin t+5\cos t),\, −20e^{−5t}⟩\)

\(\vecs a(t)=⟨e^{−5t}(−\sin t−5\cos t)−5e^{−5t}(\cos t−5\sin t), \; −e^{−5t}(\cos t−5\sin t)+5e^{−5t}(\sin t+5\cos t),\; 100e^{−5t}⟩\)

21) Find the maximum speed of a point on the circumference of an automobile tire of radius 1 ft when the automobile is traveling at 55 mph.

22) Find the position vector-valued function \(\vecs r(t)\), given that \(\vecs a(t)=\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}, \quad \vecs v(0)=2\,\hat{\mathbf{j}}\),   and   \(\vecs r(0)=2\,\hat{\mathbf{i}}\).

23) Find \(\vecs r(t)\) given that \(\vecs a(t)=−32\,\hat{\mathbf{j}}, \vecs v(0)=600\sqrt{3} \,\hat{\mathbf{i}}+600\,\hat{\mathbf{j}}\), and \(\vecs r(0)=\vecs 0\).

24) The acceleration of an object is given by \(\vecs a(t)=t\,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\). The velocity at \(t=1\) sec is \(\vecs v(1)=5\,\hat{\mathbf{j}}\) and the position of the object at \(t=1\) sec is \(\vecs r(1)=0\,\hat{\mathbf{i}}+0\,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\). Find the object’s position at any time.

Answer: \(\vecs r(t)=0\,\hat{\mathbf{i}}+\left(\frac{1}{6}t^3+4.5t−\frac{14}{3}\right)\,\hat{\mathbf{j}}+\left(\frac{1}{6}t^3−\frac{1}{2}t+\frac{1}{3}\right)\,\hat{\mathbf{k}}\)

25) A projectile is shot in the air from ground level with an initial velocity of 500 m/sec at an angle of 60° with the horizontal. 

a. At what time does the projectile reach maximum height?

Answer: 44.185 sec

b. What is the approximate maximum height of the projectile?

c. At what time is the maximum range of the projectile attained?

Answer: t=88.37 sec

d. What is the maximum range?

e. What is the total flight time of the projectile?

Answer: 88.37 sec

26) A projectile is fired at a height of 1.5 m above the ground with an initial velocity of 100 m/sec and at an angle of 30° above the horizontal. Use this information to answer the following questions:

a. Determine the maximum height of the projectile.

b. Determine the range of the projectile.

Answer: The range is approximately 886.29 m.

27) A golf ball is hit in a horizontal direction off the top edge of a building that is 100 ft tall. How fast must the ball be launched to land 450 ft away?

28) A projectile is fired from ground level at an angle of 8° with the horizontal. The projectile is to have a range of 50 m. Find the minimum velocity necessary to achieve this range.

Answer: v=42.16v=42.16 m/sec

29) Prove that an object moving in a straight line at a constant speed has an acceleration of zero.

30) The acceleration of an object is given by \(\vecs a(t)=t\,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\). The velocity at \(t=1\) sec is \(\vecs v(1)=5\,\hat{\mathbf{j}}\) and the position of the object at  \(t=1\) sec is \(\vecs r(0)=0\,\hat{\mathbf{i}}+0 \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}\). Find the object’s position at any time.

31)  Find the tangential and normal components of acceleration for \(\vecs r(t)=t^2\,\hat{\mathbf{i}}+2t \,\hat{\mathbf{j}}\) when \(t=1\).

Answer:  \(a_\vecs{T}=\sqrt{2}, \quad a_\vecs{N}=\sqrt{2}\)

32) Find the tangential and normal components of acceleration.

a. \(\vecs r(t)=⟨\cos(2t),\,\sin(2t),1⟩\)

b. \(\vecs r(t)=⟨e^t \cos t,\,e^t\sin t,\,e^t⟩\). The graph is shown here:

Answer: \(a_\vecs{T}=\sqrt{3}e^t, \quad a_\vecs{N}=\sqrt{2}e^t\)

c. \(\vecs r(t)=⟨\frac{2}{3}(1+t)^{3/2}, \,\frac{2}{3}(1-t)^{3/2},\,\sqrt{2}t⟩\)

d. \(\vecs r(t)=\left\langle 2t,\,t^2,\,\dfrac{t^3}{3}\right\rangle\)

Answer: \(a_\vecs{T}=2t, \quad a_\vecs{N}=2\)

e. \(\vecs r(t)=t^2\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3\,\hat{\mathbf{k}}\)

f. \(\vecs r(t)=⟨6t,\,3t^2,\,2t^3⟩\) 

Answer: \(a_\vecs{T}=\dfrac{6t +12t^3}{\sqrt{1+t^2+t^4}}, \quad a_\vecs{N}=6\sqrt{\dfrac{1+4t^2+t^4}{1+t^2+t^4}}\)

g. \(\vecs r(t)=3\cos(2πt)\,\hat{\mathbf{i}}+3\sin(2πt)\,\hat{\mathbf{j}}\)

Answer: \(a_\vecs{T}=0, \quad a_\vecs{N}=12\pi^2\)

33) Suppose that the position function for an object in three dimensions is given by the equation \(\vecs r(t)=t\cos(t)\,\hat{\mathbf{i}}+t\sin(t)\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}}\).

a. Show that the particle moves on a circular cone.

b. Find the angle between the velocity and acceleration vectors when \(t=1.5\).

c. Find the tangential and normal components of acceleration when \(t=1.5\).

Answer:  \(a_\vecs{T}=0.43\,\text{m/sec}^2, \quad a_\vecs{N}=2.46\,\text{m/sec}^2\)

34)  The force on a particle is given by \(\vecs f(t)=(\cos t)\,\hat{\mathbf{i}}+(\sin t)\,\hat{\mathbf{j}}\). The particle is located at point \((c,0)\) at \(t=0\). The initial velocity of the particle is given by \(\vecs v(0)=v_0\,\hat{\mathbf{j}}\). Find the path of the particle of mass \(m\). (Recall, \(\vecs F=m\vecs a\).)

Answer: \(\vecs r(t)=\left(\dfrac{-\cos t}{m}+c+\frac{1}{m}\right)\,\hat{\mathbf{i}}+\left(\dfrac{−\sin t}{m}+\left(v_0+\frac{1}{m}\right)t\right)\,\hat{\mathbf{j}}\)

 

Chapter Review Exercises

True or False? Justify your answer with a proof or a counterexample.

1. A parametric equation that passes through points \(P\) and \(Q\) can be given by \(\vecs r(t)=⟨t^2,\, 3t+1,\, t−2⟩,\) where \(P(1,4,−1)\) and \(Q(16,11,2).\)

2. \(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=2\vecs u′(t)×\vecs u(t)\)

Answer:

False, \(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=\vecs 0.\)

3. The curvature of a circle of radius \(r\) is constant everywhere. Furthermore, the curvature is equal to \(1/r.\)

4. The speed of a particle with a position function \(\vecs r(t)\) is \(\dfrac{\vecs r′(t)}{\|\vecs r′(t)\|}.\)

Answer:

False, it is \(\|\vecs r′(t)\|\)

 

Find the domains of the vector-valued functions.

5. \(\vecs r(t)=⟨\sin(t),\, \ln(t),\, \sqrt{t}⟩\)

6. \(\vecs r(t)=\left\langle e^t,\,\dfrac{1}{\sqrt{4−t}},\,\sec t\right\rangle\)

Answer:

\(t<4, \; t≠\dfrac{nπ}{2}\)

 

Sketch the curves for the following vector equations. Use a calculator if needed.

7. [T]  \(\vecs r(t)=⟨t^2,\, t^3⟩\)

8. [T]  \(\vecs r(t)=⟨\sin(20t)e^{−t}, \, \cos(20t)e^{−t}, \, e^{−t}⟩\)

Answer:

 

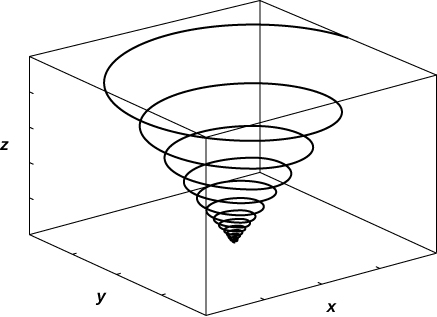
Find a vector function that describes the following curves.

9. Intersection of the cylinder \(x^2+y^2=4\) with the plane \(x+z=6\)

10. Intersection of the cone \(z=\sqrt{x^2+y^2}\) and plane \(z=y−4\)

Answer:

\(\vecs r(t)=\left\langle t, \, 2-\frac{t^2}{8},\, -2 - \frac{t^2}{8}\right\rangle\)

 

Find the derivatives of \(\vecs u(t), \, \vecs u′(t), \, \vecs u′(t)×\vecs u(t), \, \vecs u(t)×\vecs u′(t),\) and \(\vecs u(t)·\vecs u′(t).\) Find the unit tangent vector.

11.  \(\vecs u(t)=⟨e^t, \, e^{−t}⟩\)

12.  \(\vecs u(t)=⟨t^2,\, 2t+6, \, 4t^5−12⟩\)

Answer:

\(\vecs u′(t)=⟨2t, \, 2, \, 20t^4⟩,\)
\(\vecs u″(t)=⟨2, \, 0, \, 80t^3⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u′(t)×\vecs u(t)\Big]=⟨−480t^3−160t^4, \, 24+75t^2, \, 12+4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u′(t)\Big]=⟨480t^3+160t^4, \, -24-75t^2, \, -12-4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)⋅\vecs u′(t)\Big]=720t^8−9600t^3+6t^2+4,\)
unit tangent vector: \(\vecs T(t)=\dfrac{2t}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat i}+\dfrac{2}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat j}+\dfrac{20t^4}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat k}\)

 

Evaluate the following integrals.

13. \(\displaystyle ∫\left(\tan(t)\sec(t)\,\mathbf{\hat i}−te^{3t}\,\mathbf{\hat j}\right)\, dt\)

14. \(\displaystyle ∫_1^4 \vecs u(t) \, dt,\) with \(\vecs u(t)=\left\langle\dfrac{\ln t}{t}, \, \dfrac{1}{\sqrt{t}}, \, \sin\left(\frac{tπ}{4}\right)\right\rangle\)

Answer:

\(\dfrac{\ln(4^2)}{2}\,\mathbf{\hat i}+2\,\mathbf{\hat j}+\dfrac{2(2+\sqrt{2})}{\pi}\,\mathbf{\hat k}\)

 

Find the length for the following curves.

15.  \(\vecs r(t)=⟨3t,\, 4\cos t, \, 4\sin t ⟩\)  for  \(1≤t≤4\)

16.  \(\vecs r(t)=2\,\mathbf{\hat i}+t\,\mathbf{\hat j}+3t^2\,\mathbf{\hat k}\)  for  \(0≤t≤1\)

Answer:

\(\dfrac{\sqrt{37}}{2}+\frac{1}{12}\sinh^{−1} 6\)

 

Reparameterize the following functions with respect to their arc length measured from \(t=0\) in direction of increasing \(t.\)

17.  \(\vecs r(t)=2t\,\mathbf{\hat i}+(4t−5)\,\mathbf{\hat j}+(1−3t)\,\mathbf{\hat k}\)

18.  \(\vecs r(t)=\cos(2t)\,\mathbf{\hat i}+8t\,\mathbf{\hat j}−\sin(2t)\,\mathbf{\hat k}\)

Answer:

\(\vecs r(t(s))=\cos\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat i}+\frac{8s}{\sqrt{65}}\,\mathbf{\hat j}−\sin\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat k}\)

 

Find the curvature for the following vector functions.

19.  \(\vecs r(t)=(2\sin t)\,\mathbf{\hat i}−4t\,\mathbf{\hat j}+(2\cos t)\,\mathbf{\hat k}\)

20.  \(\vecs r(t)=\sqrt{2}e^t\,\mathbf{\hat i}+\sqrt{2}e^{−t}\,\mathbf{\hat j}+2t\,\mathbf{\hat k}\)

Answer:

\(\dfrac{e^{2t}}{\left(e^{2t}+1\right)^2}\)

 

21. Find the unit tangent vector, the unit normal vector, and the binormal vector for \(\vecs r(t)=2\cos t\,\mathbf{\hat i} +3t\,\mathbf{\hat j}+2sint\,\mathbf{\hat k}.\)

22. Find the tangential and normal acceleration components with the position vector \(\vecs r(t)=⟨\cos t,\, \sin t, \, e^t⟩.\)

Answer:

\(a_T=\dfrac{e^{2t}}{1+e^{2t}},\)

\(a_N=\dfrac{\sqrt{2e^{2t}+4e^{2t}\sin t\cos t+1}}{1+e^{2t}}\)

23. A Ferris wheel car is moving at a constant speed \(v\) and has a constant radius \(r.\) Find the tangential and normal acceleration of the Ferris wheel car.

24. The position of a particle is given by \(\vecs r(t)=⟨t^2, \, \ln t, \, \sin(πt)⟩,\) where \(t\) is measured in seconds and \(r\) is measured in meters. Find the velocity, acceleration, and speed functions. What are the position, velocity, speed, and acceleration of the particle at 1 sec?

Answer:

\(\vecs v(t)=\left\langle 2t,\, \frac{1}{t}, \, \pi\cos(πt)\right\rangle\text{ m/sec},\)
\(\vecs a(t)=\left\langle 2, \, −\frac{1}{t^2}, \, −\pi^2\sin(πt) \right\rangle\text{ m/sec}^2,\)
\(\text{speed}(t)=\sqrt{4t^2+\frac{1}{t^2}+\pi^2\cos^2(πt)}\text{ m/sec}\);
At \(t=1,\; \vecs r(1)=⟨1,0,0⟩\) m, \(\vecs v(1)=⟨2,−1,\pi⟩\) m/sec, \(\vecs a(1)=⟨2,−1,0⟩\) m/sec², and \(\text{speed}(1) =\sqrt{5+\pi^2}\) m/sec

 

The following problems consider launching a cannonball out of a cannon. The cannonball is shot out of the cannon with an angle \(θ\) and initial velocity \(\vecs v_0.\) The only force acting on the cannonball is gravity, so we begin with a constant acceleration \(\vecs a(t)=−g\,\mathbf{\hat j}.\)

25. Find the velocity vector function \(\vecs v(t).\)

26. Find the position vector \(\vecs r(t)\) and the parametric representation for the position.

Answer:

\(\vecs r(t)=\vecs v_0t−\dfrac{gt^2}{2}\,\mathbf{\hat j},\)
\(\vecs r(t)=⟨v_0(\cos θ)t,\,v_0(\sin θ)t,−\dfrac{gt^2}{2}⟩\)  where  \(v_0 = \|\vecs v_0\|.\)

27. At what angle do you need to fire the cannonball for the horizontal distance to be greatest? What is the total distance it would travel?