1.7: Other Types of Equations
- Last updated
- Save as PDF
- Page ID
- 29110
Learning Objectives
- Solve equations involving rational exponents.
- Solve equations using factoring.
- Solve radical equations.
- Solve absolute value equations.
- Solve other types of equations.
We have solved linear equations, rational equations, and quadratic equations using several methods. However, there are many other types of equations, and we will investigate a few more types in this section. We will look at equations involving rational exponents, polynomial equations, radical equations, absolute value equations, equations in quadratic form, and some rational equations that can be transformed into quadratics. Solving any equation, however, employs the same basic algebraic rules. We will learn some new techniques as they apply to certain equations, but the algebra never changes.
Solving Equations Involving Rational Exponents
Rational exponents are exponents that are fractions, where the numerator is a power and the denominator is a root. For example, \({16}^{\tfrac{1}{2}}\) is another way of writing \(\sqrt{16}\); \(8^{\tfrac{1}{3}}\) is another way of writing \(\sqrt[3]{8}\). The ability to work with rational exponents is a useful skill, as it is highly applicable in calculus.
We can solve equations in which a variable is raised to a rational exponent by raising both sides of the equation to the reciprocal of the exponent. The reason we raise the equation to the reciprocal of the exponent is because we want to eliminate the exponent on the variable term, and a number multiplied by its reciprocal equals \(1\). For example,
\[\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber\]
\[3\left (\dfrac{1}{3} \right )=1, \nonumber\]
and so on.
RATIONAL EXPONENTS
A rational exponent indicates a power in the numerator and a root in the denominator. There are multiple ways of writing an expression, a variable, or a number with a rational exponent:
\[a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\]
Example \(\PageIndex{1}\): Evaluating a Number Raised to a Rational Exponent
Evaluate \(8^{\tfrac{2}{3}}\)
Solution
Whether we take the root first or the power first depends on the number. It is easy to find the cube root of \(8\), so rewrite \(8^{\tfrac{2}{3}}\) as \({\left (8^{\tfrac{1}{3}} \right )}^2\).
\[\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}\]
Exercise \(\PageIndex{1}\)
Evaluate \({64}^{-\tfrac{1}{3}}\)
- Answer
-
\(\dfrac{1}{4}\)
Example \(\PageIndex{2}\): Solve the Equation Including a Variable Raised to a Rational Exponent
Solve the equation in which a variable is raised to a rational exponent: \(x^{\tfrac{5}{4}} = 32\).
Solution
The way to remove the exponent on \(x\) is by raising both sides of the equation to a power that is the reciprocal of \(\dfrac{5}{4}\), which is \(\dfrac{4}{5}\).
\[\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}\]
Exercise \(\PageIndex{2}\)
Solve the equation \(x^{\tfrac{3}{2}} = 125\).
- Answer
-
\(25\)
Example \(\PageIndex{3}\): Solving an Equation Involving Rational Exponents and Factoring
Solve \(3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}\).
Solution
This equation involves rational exponents as well as factoring rational exponents. Let us take this one step at a time. First, put the variable terms on one side of the equal sign and set the equation equal to zero.
\[\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}\]
Now, it looks like we should factor the left side, but what do we factor out? We can always factor the term with the lowest exponent. Rewrite \(x^{\tfrac{1}{2}}\) as \(x^{\tfrac{2}{4}}\). Then, factor out \(x^{\tfrac{2}{4}}\) from both terms on the left.
\[\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}\]
Where did \(x^{\tfrac{1}{4}}\) come from? Remember, when we multiply two numbers with the same base, we add the exponents. Therefore, if we multiply \(x^{\tfrac{2}{4}}\) back in using the distributive property, we get the expression we had before the factoring, which is what should happen. We need an exponent such that when added to \(\dfrac{2}{4}\) equals \(\dfrac{3}{4}\). Thus, the exponent on \(x\) in the parentheses is \(\dfrac{1}{4}\).
Let us continue. Now we have two factors and can use the zero factor theorem.
\[\begin{align*}
x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0\\
x^{\tfrac{2}{4}}&= 0\\
x&= 0\\
3x^{\tfrac{1}{4}}-1&= 0\\
3x^{\tfrac{1}{4}}&= 1\\
x^{\tfrac{1}{4}}&= \dfrac{1}{3},\qquad \text{Divide both sides by 3.}\\
{\left (x^{\tfrac{1}{4}} \right )}^4&= {\left (\dfrac{1}{3} \right )}^4, \qquad \text{Raise both sides to the reciprocal of } \dfrac{1}{4}\\
x&= \dfrac{1}{81}
\end{align*}\]
The two solutions are \(0\) and \(\dfrac{1}{81}\).
Exercise \(\PageIndex{3}\)
Solve: \({\left(x+5\right)}^{\tfrac{3}{2}}=8\).
- Answer
-
\(-1\)
Solving Equations Using Factoring
We have used factoring to solve quadratic equations, but it is a technique that we can use with many types of polynomial equations, which are equations that contain a string of terms including numerical coefficients and variables. When we are faced with an equation containing polynomials of degree higher than \(2\), we can often solve them by factoring.
POLYNOMIAL EQUATIONS
A polynomial of degree \(n\) is an expression of the type
\[a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0\]
where \(n\) is a positive integer and \(a_n ,…, a_0\) are real numbers and \(a_n≠0\).
Setting the polynomial equal to zero gives a polynomial equation. The total number of solutions (real and complex) to a polynomial equation is equal to the highest exponent \(n\).
Example \(\PageIndex{4}\): Solving a Polynomial by Factoring
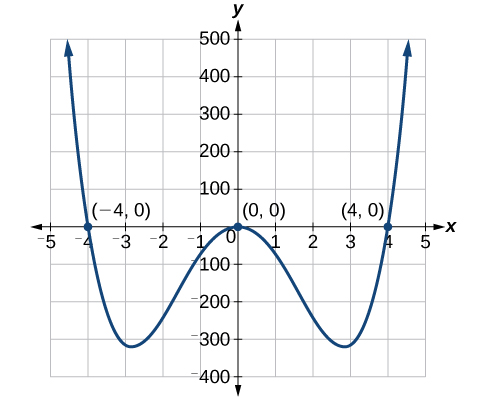
Solve the polynomial by factoring: \(5x^4 = 80x^2\).
Solution
First, set the equation equal to zero. Then factor out what is common to both terms, the GCF.
\[\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}\]
Notice that we have the difference of squares in the factor \(x^2−16\), which we will continue to factor and obtain two solutions. The first term, \(5x^2\), generates, technically, two solutions as the exponent is \(2\), but they are the same solution.
\[\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}\]
The solutions are \(0\) (double solution), \(4\), and \(−4\).
Analysis
We can see the solutions on the graph in Figure \(\PageIndex{1}\). The x-coordinates of the points where the graph crosses the \(x\)-axis are the solutions—the \(x\)-intercepts. Notice on the graph that at the solution \(0\), the graph touches the \(x\)-axis and bounces back. It does not cross the \(x\)-axis. This is typical of double solutions.
Exercise \(\PageIndex{4}\)
Solve by factoring: \(12x^4 = 3x^2\).
- Answer
-
\(x=0, x=12, x=−12\)
Example \(\PageIndex{5}\): Solve a Polynomial by Grouping
Solve a polynomial by grouping: \(x^3+x^2−9x−9=0\).
Solution
This polynomial consists of \(4\) terms, which we can solve by grouping. Grouping procedures require factoring the first two terms and then factoring the last two terms. If the factors in the parentheses are identical, we can continue the process and solve, unless more factoring is suggested.
\[\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}\]
The grouping process ends here, as we can factor \(x^2−9\) using the difference of squares formula.
\[\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}\]
The solutions are \(3\), \(−3\), and \(−1\). Note that the highest exponent is \(3\) and we obtained \(3\) solutions. We can see the solutions, the x-intercepts, on the graph in Figure \(\PageIndex{2}\).
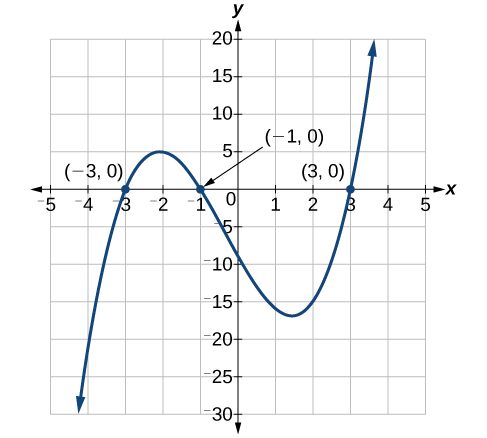
Analysis
We looked at solving quadratic equations by factoring when the leading coefficient is \(1\). When the leading coefficient is not \(1\), we solved by grouping. Grouping requires four terms, which we obtained by splitting the linear term of quadratic equations. We can also use grouping for some polynomials of degree higher than \(2\), as we saw here, since there were already four terms.
Solving Radical Equations
Radical equations are equations that contain variables in the radicand (the expression under a radical symbol), such as
\[\sqrt{3x+18}=x \nonumber\]
\[\sqrt{x+3}=x-3 \nonumber\]
\[\sqrt{x+5}-\sqrt{x-3}=2 \nonumber\]
Radical equations may have one or more radical terms, and are solved by eliminating each radical, one at a time. We have to be careful when solving radical equations, as it is not unusual to find extraneous solutions, roots that are not, in fact, solutions to the equation. These solutions are not due to a mistake in the solving method, but result from the process of raising both sides of an equation to a power. However, checking each answer in the original equation will confirm the true solutions.
RADICAL EQUATIONS
An equation containing terms with a variable in the radicand is called a radical equation.
Howto: Given a radical equation, solve it
- Isolate the radical expression on one side of the equal sign. Put all remaining terms on the other side.
- If the radical is a square root, then square both sides of the equation. If it is a cube root, then raise both sides of the equation to the third power. In other words, for an \(n^{th}\) root radical, raise both sides to the \(n^{th}\) power. Doing so eliminates the radical symbol.
- Solve the remaining equation.
- If a radical term still remains, repeat steps 1–2.
- Confirm solutions by substituting them into the original equation.
Example \(\PageIndex{6}\): Solving an Equation with One Radical
Solve \(\sqrt{15−2x}=x\).
Solution
The radical is already isolated on the left side of the equal side, so proceed to square both sides.
\[\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}\]
We see that the remaining equation is a quadratic. Set it equal to zero and solve.
\[\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}\]
The proposed solutions are \(−5\) and \(3\). Let us check each solution back in the original equation. First, check \(x=−5\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}\]
This is an extraneous solution. While no mistake was made solving the equation, we found a solution that does not satisfy the original equation.
Check \(x=3\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}\]
The solution is \(3\).
Exercise \(\PageIndex{5}\)
Solve the radical equation: \(\sqrt{x+3}=3x-1\)
- Answer
-
\(x=1\), extraneous solution \(x=−\dfrac{2}{9}\)
Example \(\PageIndex{7}\): Solving a Radical Equation Containing Two Radicals
Solve \(\sqrt{2x+3}+\sqrt{x-2}=4\)
Solution
As this equation contains two radicals, we isolate one radical, eliminate it, and then isolate the second radical.
\[\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber\]
\[\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}\]
Use the perfect square formula to expand the right side: \({(a−b)}^2=a^2−2ab+b^2\).
\[\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}\]
Now that both radicals have been eliminated, set the quadratic equal to zero and solve.
\[\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}\]
The proposed solutions are \(3\) and \(83\). Check each solution in the original equation.
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}\]
One solution is \(3\).
Check \(x=83\).
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}\]
The only solution is \(3\). We see that \(x=83\) is an extraneous solution.
Exercise \(\PageIndex{6}\)
Solve the equation with two radicals: \(\sqrt{3x+7}+\sqrt{x+2}=1\)
- Answer
-
\(x=−2\), extraneous solution \(x=−1\)
Solving an Absolute Value Equation
Next, we will learn how to solve an absolute value equation. To solve an equation such as \(|2x−6|=8\), we notice that the absolute value will be equal to \(8\) if the quantity inside the absolute value bars is \(8\) or \(−8\). This leads to two different equations we can solve independently.
\[\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}\]
OR
\[\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}\]
Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.
ABSOLUTE VALUE EQUATIONS
The absolute value of \(x\) is written as \(|x|\). It has the following properties:
If \(x≥0\), then \(|x|=x\).If \(x<0\), then \(x=−x\).
For real numbers \(A\) and \(B\), an equation of the form \(|A|=B\), with \(B≥0\), will have solutions when \(A=B\) or \(A=−B\). If \(B<0\), the equation \(|A|=B\) has no solution.
An absolute value equation in the form \(|ax+b|=c\) has the following properties:
- If \(c<0\),\(|ax+b|=c\) has no solution.
- If \(c=0\),\(|ax+b|=c\)has one solution.
- If \(c>0\),\(|ax+b|=c\) has two solutions.
How to
Given an absolute value equation, solve it.
- Isolate the absolute value expression on one side of the equal sign.
- If \(c>0\), write and solve two equations: \(ax+b=c\) and \(ax+b=−c\).
Example \(\PageIndex{8}\): Solving Absolute Value Equations
Solve the following absolute value equations:
- \(|6x+4|=8\)
- \(|3x+4|=−9\)
- \(|3x−5|−4=6\)
- \(|−5x+10|=0\)
Solution
- \(|6x+4|=8\)
Write two equations and solve each:
\[\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}\]
OR
\[\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}\]
The two solutions are \(\dfrac{2}{3}\) and \(−2\).
- \(|3x+4|=−9\)
There is no solution as an absolute value cannot be negative.
- \(|3x−5|−4=6\)
Isolate the absolute value expression and then write two equations.
\[\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}\]
OR
\[\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}\]
There are two solutions: \(5\), and \(-\dfrac{5}{3}\).
- \(|−5x+10|=0\)
The equation is set equal to zero, so we have to write only one equation.
\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]
There is one solution: \(2\).
Exercise \(\PageIndex{7}\)
Solve the absolute value equation: \(|1−4x|+8=13\).
- Answer
-
\(x=−1, x=\dfrac{3}{2}\)
Solving Other Types of Equations
There are many other types of equations in addition to the ones we have discussed so far. We will see more of them throughout the text. Here, we will discuss equations that are in quadratic form, and rational equations that result in a quadratic.
Solving Equations in Quadratic Form
Equations in quadratic form are equations with three terms. The first term has a power other than \(2\). The middle term has an exponent that is one-half the exponent of the leading term. The third term is a constant. We can solve equations in this form as if they were quadratic. A few examples of these equations include \(x^4−5x^2+4=0\),\(x^6+7x^3−8=0\), and \(x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0\). In each one, doubling the exponent of the middle term equals the exponent on the leading term. We can solve these equations by substituting a variable for the middle term.
QUADRATIC FORM
If the exponent on the middle term is one-half of the exponent on the leading term, we have an equation in quadratic form, which we can solve as if it were a quadratic. We substitute a variable for the middle term to solve equations in quadratic form.
Howto: Given an equation quadratic in form, solve it
- Identify the exponent on the leading term and determine whether it is double the exponent on the middle term.
- If it is, substitute a variable, such as \(u\), for the variable portion of the middle term.
- Rewrite the equation so that it takes on the standard form of a quadratic.
- Solve using one of the usual methods for solving a quadratic.
- Replace the substitution variable with the original term.
- Solve the remaining equation.
Example \(\PageIndex{9}\): Solving a Fourth-degree Equation in Quadratic Form
Solve this fourth-degree equation: \(3x^4−2x^2−1=0\).
Solution
This equation fits the main criteria, that the power on the leading term is double the power on the middle term. Next, we will make a substitution for the variable term in the middle. Let \(u =x^2\). Rewrite the equation in \(u\).
\[3u^2−2u−1=0 \nonumber\]
Now solve the quadratic.
\[\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}\]
Solve each factor and replace the original term for \(u\).
\[\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}\]
The solutions are \(x=±i\sqrt{\dfrac{1}{3}}\) and \(x=±1\)
Exercise \(\PageIndex{8}\)
Solve using substitution: \(x^4−8x^2−9=0\).
- Answer
-
\(x=−3,3,−i,i\)
Example \(\PageIndex{10}\): Solving an Equation in Quadratic Form Containing a Binomial
Solve the equation in quadratic form: \({(x+2)}^2+11(x+2)−12=0\).
Solution
This equation contains a binomial in place of the single variable. The tendency is to expand what is presented. However, recognizing that it fits the criteria for being in quadratic form makes all the difference in the solving process. First, make a substitution, letting \(u =x+2\). Then rewrite the equation in \(u\).
\[\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}\]
Solve using the zero-factor property and then replace \(u\) with the original expression.
\[\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}\]
The second factor results in
\[\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}\]
We have two solutions: \(−14\), and \(−1\).
Exercise \(\PageIndex{9}\)
Solve: \({(x−5)}^2−4(x−5)−21=0\).
- Answer
-
\(x=2,x=12\)
Solving Rational Equations Resulting in a Quadratic
Earlier, we solved rational equations. Sometimes, solving a rational equation results in a quadratic. When this happens, we continue the solution by simplifying the quadratic equation by one of the methods we have seen. It may turn out that there is no solution.
Example \(\PageIndex{11}\): Solving a Rational Equation Leading to a Quadratic
Solve the following rational equation: \(\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}\)
Solution
We want all denominators in factored form to find the LCD. Two of the denominators cannot be factored further. However, \(x^2−1=(x+1)(x−1)\). Then, the LCD is \((x+1)(x−1)\). Next, we multiply the whole equation by the LCD.
\[\begin{align*} (x+1)(x-1)\left (\dfrac{-4x}{x-1}+\dfrac{4}{x+1} \right )&= \left (\dfrac{-8}{x^2-1} \right )(x+1)(x-1)\\ -4x(x+1)+4(x-1)&= -8\\ -4x^2-4x+4x-4&= -8\\ -4x^2+4&= 0\\
-4(x^2-1)&= 0\\ -4(x+1)(x-1)&= 0\\ x&= -1\\ x&= 1 \end{align*}\]
In this case, either solution produces a zero in the denominator in the original equation. Thus, there is no solution.
Exercise \(\PageIndex{10}\)
Solve \(\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}\)
- Answer
-
\(x=−1, x= 0\) is not a solution.
Media
Access these online resources for additional instruction and practice with different types of equations.
- Rational Equation with no Solution
- Solving equations with rational exponents using reciprocal powers
- Solving radical equations part 1 of 2
- Solving radical equations part 2 of 2
Key Concepts
- Rational exponents can be rewritten several ways depending on what is most convenient for the problem. To solve, both sides of the equation are raised to a power that will render the exponent on the variable equal to \(1\). See Example, Example, and Example.
- Factoring extends to higher-order polynomials when it involves factoring out the GCF or factoring by grouping. See Example and Example.
- We can solve radical equations by isolating the radical and raising both sides of the equation to a power that matches the index. See Example and Example.
- To solve absolute value equations, we need to write two equations, one for the positive value and one for the negative value. See Example.
- Equations in quadratic form are easy to spot, as the exponent on the first term is double the exponent on the second term and the third term is a constant. We may also see a binomial in place of the single variable. We use substitution to solve. See Example and Example.
- Solving a rational equation may also lead to a quadratic equation or an equation in quadratic form. See Example.


