4.11: Chapter 4 Review Exercises

True or False? Justify your answer with a proof or a counterexample. Assume that $f(x)$ is continuous and differentiable unless stated otherwise.

1) If $f(−1)=−6$ and $f(1)=2$, then there exists at least one point $x∈[−1,1]$ such that $f′(x)=4.$

Answer

True, by Mean Value Theorem

2) If $f′(c)=0,$ there is a maximum or minimum at $x=c.$

3) There is a function such that $f(x)<0,f′(x)>0,$ and $f''(x)<0.$ (A graphical “proof” is acceptable for this answer.)

Answer

True

4) There is a function such that there is both an inflection point and a critical point for some value $x=a.$

5) Given the graph of $f′$, determine where $f$ is increasing or decreasing.

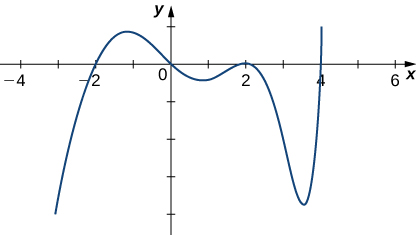
Answer

Increasing: $(−2,0)∪(4,∞)$, decreasing: $(−∞,−2)∪(0,4)$

6) The graph of $f$ is given below. Draw $f′$.

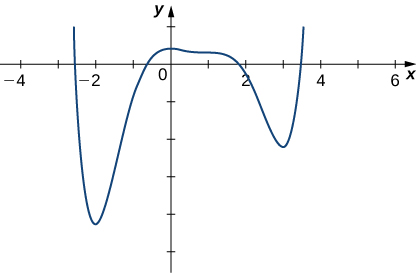
7) Find the linear approximation $L(x)$ to $y=x^2+\tan(πx)$ near $x=\frac{1}{4}.$

Answer

$L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)\left(x−\frac{1}{4}\right)$

8) Find the differential of $y=x^2−5x−6$ and evaluate for $x=2$ with $dx=0.1.$

Find the critical points and the local and absolute extrema of the following functions on the given interval.

9) $f(x)=x+\sin^2(x)$ over $[0,π]$

Answer

Critical point: $x=\frac{3π}{4},$
Absolute minimum: $0$ when $x=0,$
Absolute maximum: $π$ when $x=π$

Solution:

10) $f(x)=3x^4−4x^3−12x^2+6$ over $[−3,3]$

Determine over which intervals the following functions are increasing, decreasing, concave up, and concave down.

11) $x(t)=3t^4−8t^3−18t^2$

Answer

Increasing: $(−1,0)∪(3,∞),$
Decreasing: $(−∞,−1)∪(0,3),$
Concave up: $\left(−∞,\frac{1}{3}\left(2−\sqrt{13}\right)\right)∪\left(\frac{1}{3}\left(2+\sqrt{13}\right),∞\right)$,
Concave down: $\left(\frac{1}{3}\left(2−\sqrt{13}\right),\frac{1}{3}\left(2+\sqrt{13}\right)\right)$

12) $y=x+\sin(πx)$

13) $g(x)=x−\sqrt{x}$

Answer

Increasing: $\left(\frac{1}{4},∞\right),$
Decreasing: $\left(0,\frac{1}{4}\right)$,
Concave up: $(0,∞),$
Concave down: nowhere

14) $f(θ)=\sin(3θ)$

Evaluate the following limits.

15) $\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Answer

$3$

16) $\displaystyle \lim_{x→∞}\cos\left(\frac{1}{x}\right)$

17) $\displaystyle \lim_{x→1}\frac{x−1}{\sin(πx)}$

Answer

$−\frac{1}{π}$

18) $\displaystyle \lim_{x→∞}(3x)^{1/x}$

Use Newton’s method to find the first two iterations, given the starting point.

19) $y=x^3+1,\quad x_0=0.5$

Answer

$x_1=−1,\; x_2=−1$

20) $\dfrac{1}{x+1}=\dfrac{1}{2}, \quad x_0=0$

Find the antiderivatives $F(x)$ of the following functions.

21) $g(x)=\sqrt{x}−\dfrac{1}{x^2}$

Answer

$F(x)=\dfrac{2x^{3/2}}{3}+\dfrac{1}{x}+C$

22) $f(x)=2x+6\cos x,\quad F(π)=π^2+2$

Graph the following functions by hand. Make sure to label the inflection points, critical points, zeros, and asymptotes.

23) $y=\dfrac{1}{x(x+1)^2}$

Answer

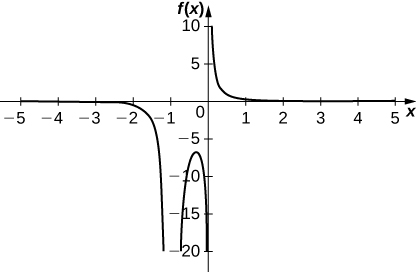
Inflection points: none;
Critical points: $x=−\frac{1}{3}$;
Zeros: none;
Vertical asymptotes: $x=−1, \; x=0$;
Horizontal asymptote: $y=0$

24) $y=x−\sqrt{4−x^2}$

25) A car is being compacted into a rectangular solid. The volume is decreasing at a rate of $2\, \text{m}^3/\text{sec}$. The length and width of the compactor are square, but the height is not the same length as the length and width. If the length and width walls move toward each other at a rate of $0.25$ m/sec, find the rate at which the height is changing when the length and width are $2$ m and the height is $1.5$ m.

Answer

The height is decreasing at a rate of $0.125$ m/sec

26) A rocket is launched into space; its kinetic energy is given by $K(t)=\frac{1}{2}m(t)v(t)^2$, where $K$ is the kinetic energy in joules, $m$ is the mass of the rocket in kilograms, and $v$ is the velocity of the rocket in meters/second. Assume the velocity is increasing at a rate of $15 \,\text{m/sec}^2$ and the mass is decreasing at a rate of $10$ kg/sec because the fuel is being burned. At what rate is the rocket’s kinetic energy changing when the mass is $2000$ kg and the velocity is $5000$ m/sec? Give your answer in mega-Joules (MJ), which is equivalent to $10^6$ J.

27) The famous Regiomontanus’ problem for angle maximization was proposed during the $15^\text{th}$ century. A painting hangs on a wall with the bottom of the painting a distance $a$ feet above eye level, and the top $b$ feet above eye level. What distance $x$ (in feet) from the wall should the viewer stand to maximize the angle subtended by the painting, $θ$?

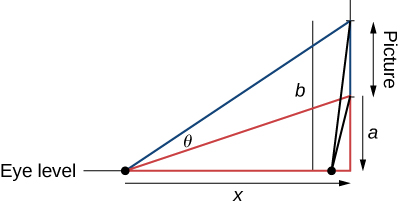
Answer

$x=\sqrt{ab}$ feet

28) An airline sells tickets from Tokyo to Detroit for $$1200.$ There are $500$ seats available and a typical flight books $350$ seats. For every $$10$ decrease in price, the airline observes an additional five seats sold. What should the fare be to maximize profit? How many passengers would be onboard?