1.5E: Exercises for Section 1.6

Last updated
Save as PDF

Page ID: 102688

Zoya Kravets
Mission College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 4, evaluate the given exponential functions as indicated, accurate to two significant digits after the decimal.

1) $f(x)=5^x$

a. $x=3$

b. $x=\frac{1}{2}$

c. $x=\sqrt{2}$

Answer: a. $125$
b. $2.24$
c. $9.74$

2) $f(x)=(0.3)^x$

a. $x=−1$

b. $x=4$

c. $x=−1.5$

3) $f(x)=10^x$

a. $x=−2$

b. $x=4$

c. $x=\frac{5}{3}$

Answer: a. $0.01$
b. $10,000$
c. $46.42$

4) $f(x)=e^x$

a. $x=2$

b. $x=−3.2$

c. $x=π$

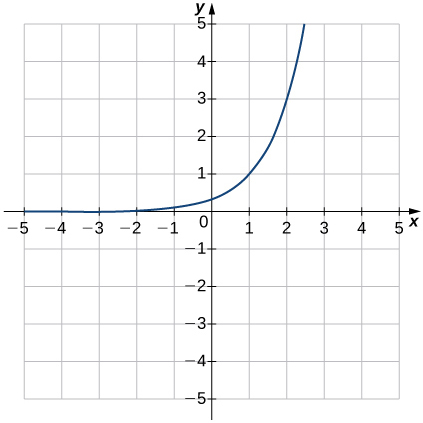
In exercises 5 - 10, match the exponential equation to the correct graph.

a. $y=4^{−x}$

b. $y=3^{x−1}$

c. $y=2^{x+1}$

d. $y=\left(\frac{1}{2}\right)^x+2$

e. $y=−3^{−x}$

f. $y=1−5^x$

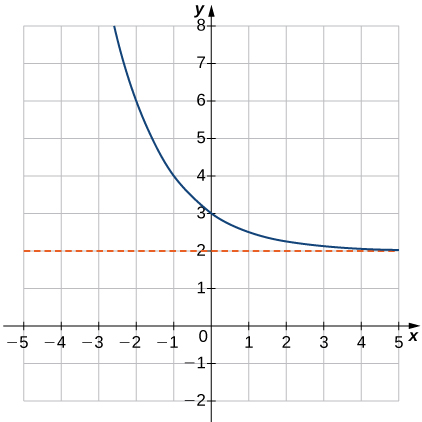
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -2 to 8. The graph is of a decreasing curved function. The function decreases until it approaches the line “y = 2”, but never touches this line. The y intercept is at the point (0, 3) and there is no x intercept.$

Answer: d

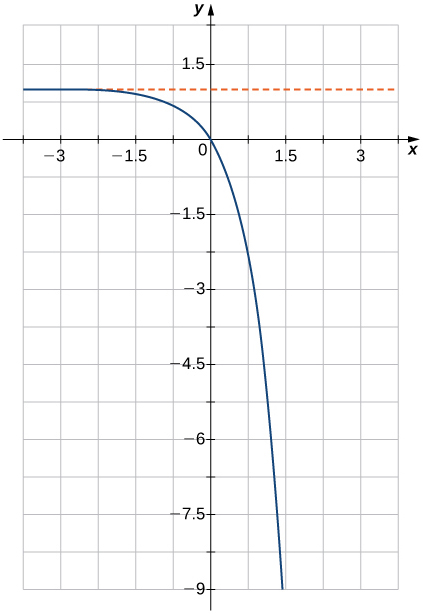
$An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -9 to 2. The graph is of a function that starts slightly below the line “y = 1” and begins decreasing rapidly in a curve. The x intercept and y intercept are both at the origin.$

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved increasing function that starts slightly above the x axis and begins increasing rapidly. There is no x intercept and the y intercept is at the point (0, (1/3)). Another point of the graph is at (1, 1).$

Answer: b

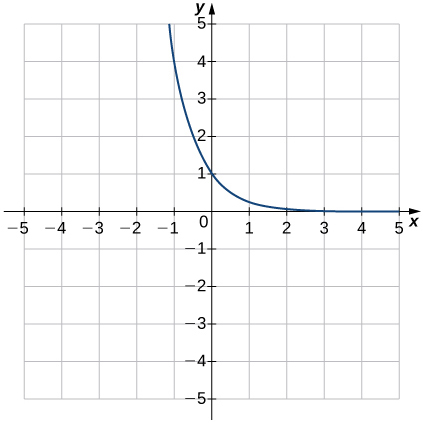
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved decreasing function that decreases until it comes close the x axis without touching it. There is no x intercept and the y intercept is at the point (0, 1). Another point of the graph is at (-1, 4).$

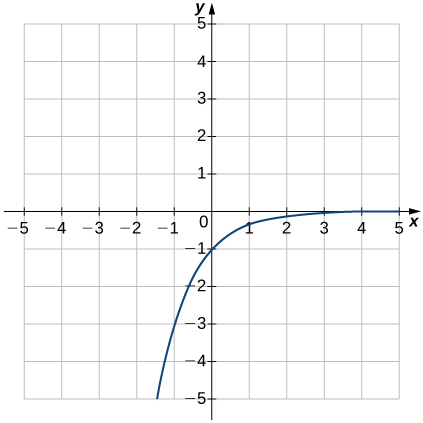
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved increasing function that increases until it comes close the x axis without touching it. There is no x intercept and the y intercept is at the point (0, -1). Another point of the graph is at (-1, -3).$

Answer: e

10)

In exercises 11 - 17, sketch the graph of the exponential function. Determine the domain, range, and horizontal asymptote.

11) $f(x)=e^x+2$

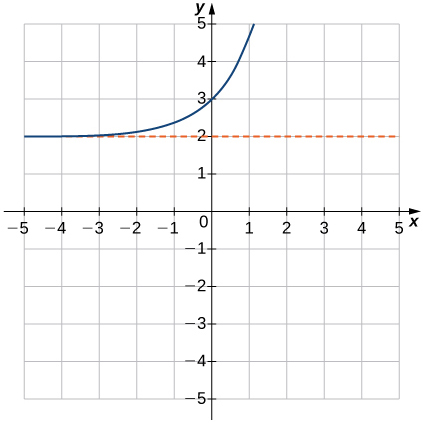
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved increasing function that starts slightly above the line “y = 2” and begins increasing rapidly. There is no x intercept and the y intercept is at the point (0, 3).$

Answer: Domain: all real numbers, Range: $(2,∞),\; y=2$

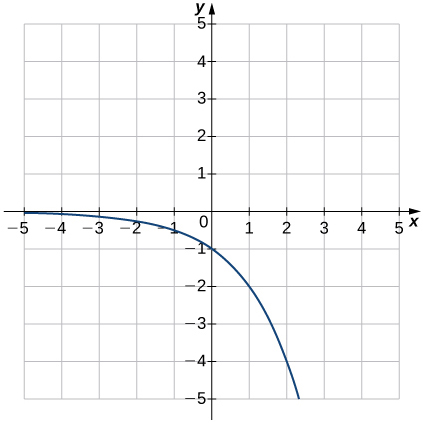
12) $f(x)=−2^x$

$alt$

13) $f(x)=3^{x+1}$

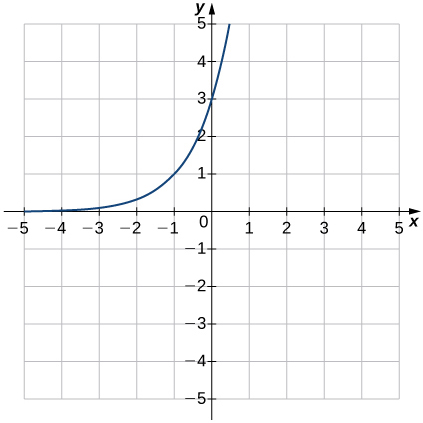
Answer: Domain: all real numbers, Range: $(0,∞),\; y=0$

14) $f(x)=4^x−1$

$alt$

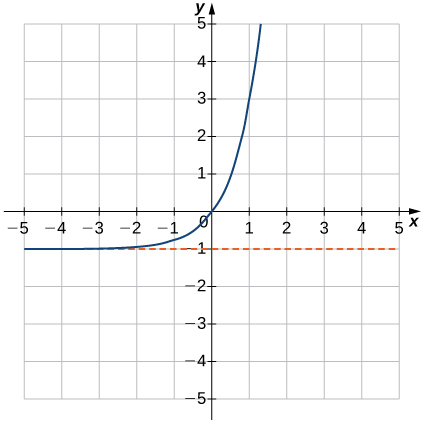
15) $f(x)=1−2^{−x}$

$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved increasing function that increases until it comes close the line “y = 1” without touching it. There x intercept and the y intercept are both at the origin. Another point of the graph is at (-1, -1).$

Answer: Domain: all real numbers, Range: $(−∞,1),\; y=1$

16) $f(x)=5^{x+1}+2$

$alt$

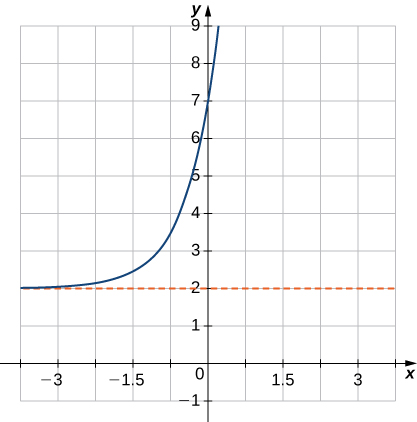
17) $f(x)=e^{−x}−1$

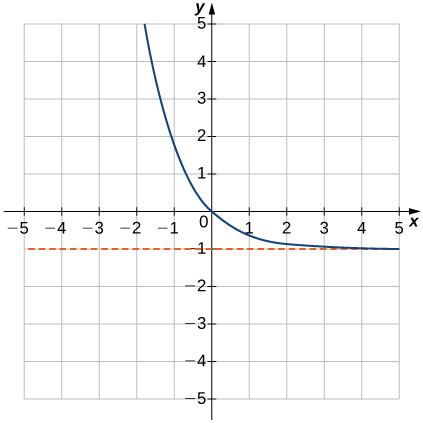
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of a curved decreasing function that decreases until it comes close the line “y = -1” without touching it. There x intercept and the y intercept are both at the origin. There is an approximate point on the graph at (-1, 1.7).$

Answer: Domain: all real numbers, Range: $(−1,∞), \;y=−1$

In exercises 18 - 25, write the equation in equivalent exponential form.

18) $\log_3 81=4$

19) $\log_8 2=\frac{1}{3}$

Answer: $8^{1/3}=2$

20) $\log_5 1=0$

21) $\log_5 25=2$

Answer: $5^2=25$

22) $\log 0.1=−1$

23) $\ln\left(\frac{1}{e^3}\right)=−3$

Answer: $e^{−3}=\dfrac{1}{e^3}$

24) $\log_9 3=0.5$

25) $\ln 1=0$

Answer: $e^0=1$

In exercises 26 - 35, write the equation in equivalent logarithmic form.

26) $2^3=8$

27) $4^{−2}=\frac{1}{16}$

Answer: $\log_4\left(\frac{1}{16}\right)=−2$

28) $10^2=100$

29) $9^0=1$

Answer: $\log_9 1=0$

30) $\left(\frac{1}{3}\right)^3=\frac{1}{27}$

31) $\sqrt[3]{64}=4$

Answer: $\log_{64}4=\frac{1}{3}$

32) $e^x=y$

33) $9^y=150$

Answer: $\log_9 150=y$

34) $b^3=45$

35) $4^{-3/2}=0.125$

Answer: $\log_4 0.125=−\frac{3}{2}$

In exercises 36 - 41, sketch the graph of the logarithmic function. Determine the domain, range, and vertical asymptote.

36) $f(x)=3+\ln x$

$alt$

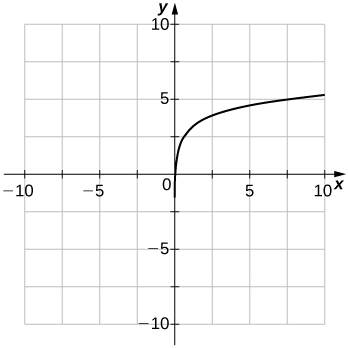
37) $f(x)=\ln(x−1)$

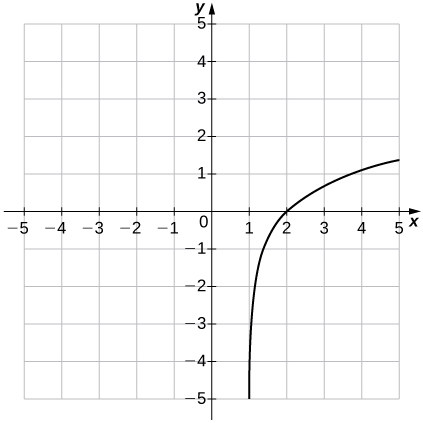
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of an increasing curved function which starts slightly to the right of the vertical line “x = 1”. There is no y intercept and the x intercept is at the approximate point (2, 0).$

Answer: Domain: $(1,∞)$, Range: $(−∞,∞),\; x=1$

38) $f(x)=\ln(−x)$

$alt$

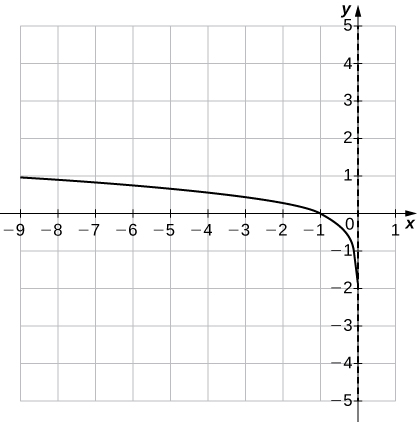
39) $f(x)=1−\ln x$

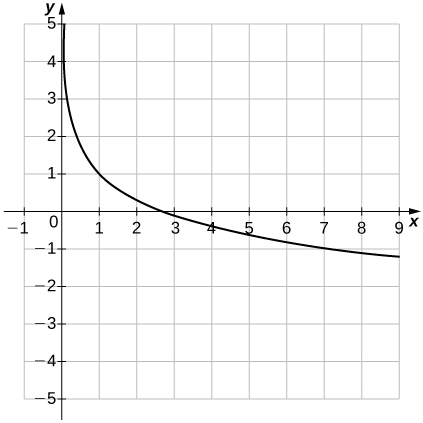
$An image of a graph. The x axis runs from -1 to 9 and the y axis runs from -5 to 5. The graph is of a decreasing curved function which starts slightly to the right of the y axis. There is no y intercept and the x intercept is at the point (e, 0).$

Answer: Domain: $(0,∞)$, Range: $(−∞,∞),\; x=0$

40) $f(x)=\log x−1$

$221$

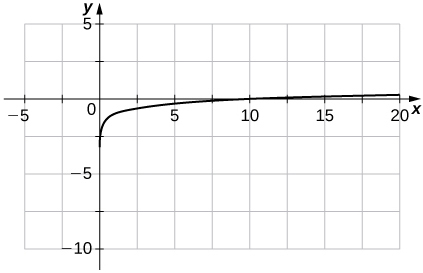
41) $f(x)=\ln(x+1)$

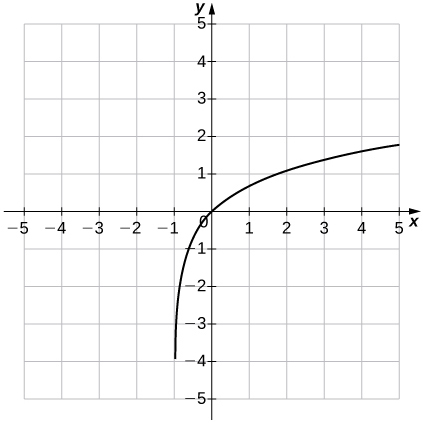
$An image of a graph. The x axis runs from -5 to 5 and the y axis runs from -5 to 5. The graph is of an increasing curved function which starts slightly to the right of the vertical line “x = -1”. There y intercept and the x intercept are both at the origin.$

Answer: Domain: $(−1,∞)$, Range: $(−∞,∞)$, $x=−1$

In exercises 42 - 47, use properties of logarithms to write the expressions as a sum, difference, and/or product of logarithms.

42) $\log x^4y$

43) $\log_3\frac{9a^3}{b}$

Answer: $2+3\log_3 a−\log_3 b$

44) $\ln a\sqrt[3]{b}$

45) $\log_5\sqrt{125xy^3}$

Answer: $\frac{3}{2}+\frac{1}{2}\log_5 x+\frac{3}{2}\log_5 y$

46) $\log_4 \frac{\sqrt[3]{xy}}{64}$

47) $\ln\left(\frac{6}{\sqrt{e^3}}\right)$

Answer: $−\frac{3}{2}+\ln 6$

In exercises 48 - 55, solve the exponential equation exactly.

48) $5^x=125$

49) $e^{3x}−15=0$

Answer: $\frac{\ln 15}{3}$

50) $8^x=4$

51) $4^{x+1}−32=0$

Answer: $\frac{3}{2}$

52) $3^{x/14}=\frac{1}{10}$

53) $10^x=7.21$

Answer: $\log 7.21$

54) $4⋅2^{3x}−20=0$

55) $7^{3x−2}=11$

Answer: $\frac{2}{3}+\frac{\log 11}{3\log 7}$

In exercises 56 - 63, solve the logarithmic equation exactly, if possible.

56) $\log_3 x=0$

57) $\log_5 x=−2$

Answer: $x=\frac{1}{25}$

58) $\log_4(x+5)=0$

59) $\log(2x−7)=0$

Answer: $x=4$

60) $\ln\sqrt{x+3}=2$

61) $\log_6(x+9)+\log_6 x=2$

Answer: $x=3$

62) $\log_4(x+2)−\log_4(x−1)=0$

63) $\ln x+\ln(x−2)=\ln 4$

Answer: $1+\sqrt{5}$

In exercises 64 - 69, use the change-of-base formula and either base $10$ or base $e$ to evaluate the given expressions. Answer in exact form and in approximate form, rounding to four decimal places.

64) $\log_5 47$

65) $\log_7 82$

Answer: $\dfrac{\log 82}{\log 7}≈2.2646$

66) $\log_6 103$

67) $\log_{0.5}211$

Answer: $\dfrac{\log 211}{\log 0.5}≈−7.7211$

68) $\log_2 π$

69) $\log_{0.2}0.452$

Answer: $\dfrac{\log 0.452}{\log 0.2}≈0.4934$

70) Rewrite the following expressions in terms of exponentials and simplify.

a. $2\cosh(\ln x)$ b. $\cosh 4x+\sinh 4x$ c. $\cosh 2x−\sinh 2x$ d. $\ln(\cosh x+\sinh x)+\ln(\cosh x−\sinh x)$

71) [T] The number of bacteria $N$ in a culture after $t$ days can be modeled by the function $N(t)=1300⋅(2)^{t/4}$. Find the number of bacteria present after $15$ days.

Answer: $\sim 17,491$

72) [T] The demand $D$ (in millions of barrels) for oil in an oil-rich country is given by the function $D(p)=150⋅(2.7)^{−0.25p}$, where $p$ is the price (in dollars) of a barrel of oil. Find the amount of oil demanded (to the nearest million barrels) when the price is between $15 and $20.

73) [T] The amount $A$ of a $100,000 investment paying continuously and compounded for t years is given by $A(t)=100,000⋅e^{0.055t}$. Find the amount $A$ accumulated in $5$ years.

Answer: Approximately $131,653 is accumulated in 5 years.

74) [T] An investment is compounded monthly, quarterly, or yearly and is given by the function $A=P\left(1+\frac{j}{n}\right)^{nt}$, where $A$ is the value of the investment at time $t$, $P$ is the initial principle that was invested, $j$ is the annual interest rate, and $n$ is the number of time the interest is compounded per year. Given a yearly interest rate of 3.5% and an initial principle of $100,000, find the amount $A$ accumulated in 5 years for interest that is compounded a. daily, b., monthly, c. quarterly, and d. yearly.

75) [T] The concentration of hydrogen ions in a substance is denoted by $[H+]$, measured in moles per liter. The pH of a substance is defined by the logarithmic function $pH=−\log[H+]$. This function is used to measure the acidity of a substance. The pH of water is 7. A substance with a pH less than 7 is an acid, whereas one that has a pH of more than 7 is a base.

a. Find the pH of the following substances. Round answers to one digit.

b. Determine whether the substance is an acid or a base.

i. Eggs: $[H+]=1.6×10^{−8}$ mol/L

ii. Beer: $[H+]=3.16×10^{−3}$ mol/L

iii. Tomato Juice: $[H+]=7.94×10^{−5}$ mol/L

Answer: i. a. pH = 8 b. Base
ii. a. pH = 3 b. Acid
iii. a. pH = 4 b. Acid

76) [T] Iodine-131 is a radioactive substance that decays according to the function $Q(t)=Q_0⋅e^{−0.08664t}$, where $Q_0$ is the initial quantity of a sample of the substance and $t$ is in days. Determine how long it takes (to the nearest day) for 95% of a quantity to decay.

77) [T] According to the World Bank, at the end of 2013 $(t=0)$ the U.S. population was 316 million and was increasing according to the following model:

\[P(t)=316e^{0.0074t}, \nonumber \]

where $P$ is measured in millions of people and $t$ is measured in years after 2013.

a. Based on this model, what will be the population of the United States in 2020?

b. Determine when the U.S. population will be twice what it is in 2013.

Answer: a. $\sim 333$ million
b. 94 years from 2013, or in 2107

78) [T] The amount $A$ accumulated after $1000$ dollars is invested for $t$ years at an interest rate of 4% is modeled by the function $A(t)=1000(1.04)^t$.

a. Find the amount accumulated after $5$ years and $10$ years.

b. Determine how long it takes for the original investment to triple.

79) [T] A bacterial colony grown in a lab is known to double in number in $12$ hours. Suppose, initially, there are $1000$ bacteria present.

a. Use the exponential function $Q=Q_0e^{kt}$ to determine the value $k$, which is the growth rate of the bacteria. Round to four decimal places.

b. Determine approximately how long it takes for $200,000$ bacteria to grow.

Answer: a. $k≈0.0578$
b. ≈$92$ hours

80) [T] The rabbit population on a game reserve doubles every $6$ months. Suppose there were $120$ rabbits initially.

a. Use the exponential function $P=P_0a^t$ to determine the growth rate constant $a$. Round to four decimal places.

b. Use the function in part a. to determine approximately how long it takes for the rabbit population to reach 3500.

81) [T] The 1906 earthquake in San Francisco had a magnitude of 8.3 on the Richter scale. At the same time, in Japan, an earthquake with magnitude 4.9 caused only minor damage. Approximately how much more energy was released by the San Francisco earthquake than by the Japanese earthquake?

Answer: The San Francisco earthquake had $10^{3.4}$ or $\sim 2512$ times more energy than the Japan earthquake.

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors