2.2E: Exercises for Section 2.2

Last updated
Save as PDF

Page ID: 102695

Zoya Kravets
Mission College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Intuitive Definition of Limits

For exercises 1 - 2, consider the function $f(x)=\dfrac{x^2−1}{|x−1|}$.

1) [T] Complete the following table for the function. Round your solutions to four decimal places.

$x$	$f(x)$	$x$	$f(x)$
0.9	a.	1.1	e.
0.99	b.	1.01	f.
0.999	c.	1.001	g.
0.9999	d.	1.0001	h.

2) What do your results in the preceding exercise indicate about the two-sided limit $\displaystyle \lim_{x→1}f(x)$? Explain your response.

Answer: $\displaystyle \lim_{x \to 1}f(x)$ does not exist because $\displaystyle \lim_{x \to 1^−}f(x)=−2≠\lim_{x \to 1^+}f(x)=2$.

For exercises 3 - 5, consider the function $f(x)=(1+x)^{1/x}$.

3) [T] Make a table showing the values of $f$ for $x=−0.01,\;−0.001,\;−0.0001,\;−0.00001$ and for $x=0.01,\;0.001,\;0.0001,\;0.00001$. Round your solutions to five decimal places.

$x$	$f(x)$	$x$	$f(x)$
-0.01	a.	0.01	e.
-0.001	b.	0.001	f.
-0.0001	c.	0.0001	g.
-0.00001	d.	0.00001	h.

4) What does the table of values in the preceding exercise indicate about the function $f(x)=(1+x)^{1/x}$?

Answer: $\displaystyle \lim_{x \to 0}(1+x)^{1/x}\approx 2.7183$.

5) To which mathematical constant do the values in the preceding exercise appear to be approaching? This is the actual limit here.

In exercises 6 - 8, use the given values to set up a table to evaluate the limits. Round your solutions to eight decimal places.

6) [T] $\displaystyle \lim_{x \to 0}\frac{\sin 2x}{x};\quad ±0.1,\; ±0.01, \; ±0.001, \;±.0001$

$x$	$\frac{\sin 2x}{x}$	$x$	$\frac{\sin 2x}{x}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

Answer: a. 1.98669331; b. 1.99986667; c. 1.99999867; d. 1.99999999; e. 1.98669331; f. 1.99986667; g. 1.99999867; h. 1.99999999;
$\displaystyle \lim_{x \to 0}\frac{\sin 2x}{x}=2$

7) [T] $\displaystyle \lim_{x \to 0}\frac{\sin 3x}{x} ±0.1, \; ±0.01, \; ±0.001, \; ±0.0001$

$x$	$\frac{\sin 3x}{x}$	$x$	$\frac{\sin 3x}{x}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

8) Use the preceding two exercises to conjecture (guess) the value of the following limit: $\displaystyle \lim_{x \to 0}\frac{\sin ax}{x}$ for $a$, a positive real value.

Answer: $\displaystyle \lim_{x \to 0}\frac{\sin ax}{x}=a$

[T] In exercises 9 - 14, set up a table of values to find the indicated limit. Round to eight significant digits.

9) $\displaystyle \lim_{x \to 2}\frac{x^2−4}{x^2+x−6}$

$x$	$\frac{x^2−4}{x^2+x−6}$	$x$	$\frac{x^2−4}{x^2+x−6}$
1.9	a.	2.1	e.
1.99	b.	2.01	f.
1.999	c.	2.001	g.
1.9999	d.	2.0001	h.

10) $\displaystyle \lim_{x \to 1}(1−2x)$

$x$	$1−2x$	$x$	$1−2x$
0.9	a.	1.1	e.
0.99	b.	1.01	f.
0.999	c.	1.001	g.
0.9999	d.	1.0001	h.

Answer: a. −0.80000000; b. −0.98000000; c. −0.99800000; d. −0.99980000; e. −1.2000000; f. −1.0200000; g. −1.0020000; h. −1.0002000;
$ \displaystyle \lim_{x \to 1}(1−2x)=−1$

11) $\displaystyle \lim_{x \to 0}\frac{5}{1−e^{1/x}}$

$x$	$\frac{5}{1−e^{1/x}}$	$x$	$\frac{5}{1−e^{1/x}}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

12) $\displaystyle \lim_{z \to 0}\frac{z−1}{z^2(z+3)}$

$z$	$\frac{z−1}{z^2(z+3)}$	$z$	$\frac{z−1}{z^2(z+3)}$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

Answer: a. −37.931034; b. −3377.9264; c. −333,777.93; d. −33,337,778; e. −29.032258; f. −3289.0365; g. −332,889.04; h. −33,328,889
$ \displaystyle \lim_{x \to 0}\frac{z−1}{z^2(z+3)}=−∞$

13) $\displaystyle \lim_{t \to 0^+}\frac{\cos t}{t}$

$t$	$\frac{\cos t}{t}$
0.1	a.
0.01	b.
0.001	c.
0.0001	d.

14) $\displaystyle \lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}$

$x$	$\frac{1−\frac{2}{x}}{x^2−4}$	$x$	$\frac{1−\frac{2}{x}}{x^2−4}$
1.9	a.	2.1	e.
1.99	b.	2.01	f.
1.999	c.	2.001	g.
1.9999	d.	2.0001	h.

Answer: a. 0.13495277; b. 0.12594300; c. 0.12509381; d. 0.12500938; e. 0.11614402; f. 0.12406794; g. 0.12490631; h. 0.12499063;
$ \displaystyle ∴\lim_{x \to 2}\frac{1−\frac{2}{x}}{x^2−4}=0.1250=\frac{1}{8}$

[T] In exercises 15 - 16, set up a table of values and round to eight significant digits. Based on the table of values, make a guess about what the limit is. Then, use a calculator to graph the function and determine the limit. Was the conjecture correct? If not, why does the method of tables fail?

15) $\displaystyle \lim_{θ \to 0}\sin\left(\frac{π}{θ}\right)$

$θ$	$\sin\left(\frac{π}{θ}\right)$	$θ$	$\sin\left(\frac{π}{θ}\right)$
-0.1	a.	0.1	e.
-0.01	b.	0.01	f.
-0.001	c.	0.001	g.
-0.0001	d.	0.0001	h.

16) $\displaystyle \lim_{α \to 0^+} \frac{1}{α}\cos\left(\frac{π}{α}\right)$

$a$	$\frac{1}{α}\cos\left(\frac{π}{α}\right)$
0.1	a.
0.01	b.
0.001	c.
0.0001	d.

Answer

a. 10.00000; b. 100.00000; c. 1000.0000; d. 10,000.000;
Guess: $\displaystyle \lim_{α→0^+}\frac{1}{α}\cos\left(\frac{π}{α}\right)=∞$;
Actual: DNE , since the graph shows the function oscillates wildly between values approaching positive infinity and values approaching negative infinity, as the value of $α$ approaches $0$ from the positive side.

$A graph of the function (1/alpha) * cos (pi / alpha), which oscillates gently until the interval [-.2, .2], where it oscillates rapidly, going to infinity and negative infinity as it approaches the y axis.$

In exercises 17 - 20, consider the graph of the function $y=f(x)$ shown here. Which of the statements about $y=f(x)$ are true and which are false? Explain why a statement is false.

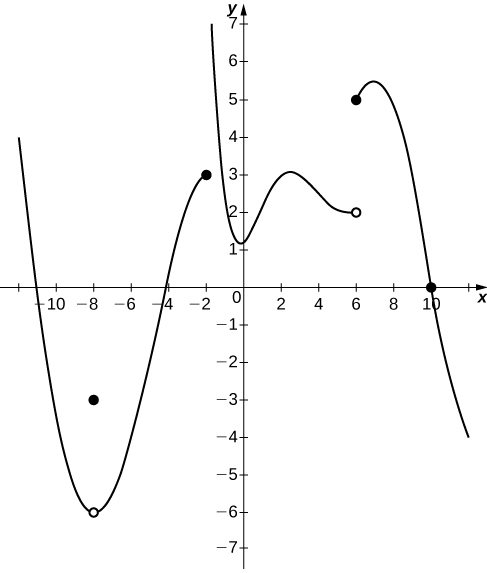
$A graph of a piecewise function with three segments and a point. The first segment is a curve opening upward with vertex at (-8, -6). This vertex is an open circle, and there is a closed circle instead at (-8, -3). The segment ends at (-2,3), where there is a closed circle. The second segment stretches up asymptotically to infinity along x=-2, changes direction to increasing at about (0,1.25), increases until about (2.25, 3), and decreases until (6,2), where there is an open circle. The last segment starts at (6,5), increases slightly, and then decreases into quadrant four, crossing the x axis at (10,0). All of the changes in direction are smooth curves.$

17) $\displaystyle \lim_{x→10}f(x)=0$

18) $\displaystyle \lim_{x→−2^+}f(x)=3$

Answer: False; $\displaystyle \lim_{x→−2^+}f(x)=+∞$

19) $\displaystyle \lim_{x→−8}f(x)=f(−8)$

20) $\displaystyle \lim_{x→6}f(x)=5$

Answer: False; $\displaystyle \lim_{x→6}f(x)$ DNE since $\displaystyle \lim_{x→6^−}f(x)=2$ and $\displaystyle \lim_{x→6^+}f(x)=5$.

In exercises 21 - 25, use the following graph of the function $y=f(x)$ to find the values, if possible. Estimate when necessary.

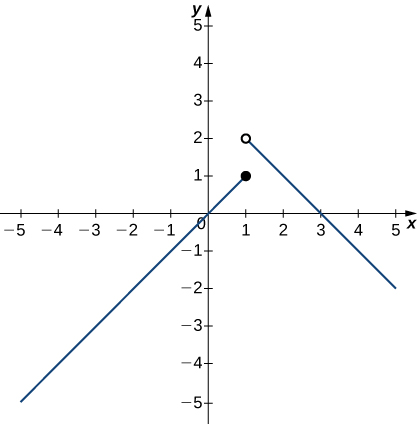
$A graph of a piecewise function with two segments. The first segment exists for x <=1, and the second segment exists for x > 1. The first segment is linear with a slope of 1 and goes through the origin. Its endpoint is a closed circle at (1,1). The second segment is also linear with a slope of -1. It begins with the open circle at (1,2).$

21) $\displaystyle \lim_{x→1^−}f(x)$

22) $\displaystyle \lim_{x→1^+}f(x)$

Answer: $2$

23) $\displaystyle \lim_{x→1}f(x)$

24) $\displaystyle \lim_{x→2}f(x)$

Answer: $1$

25) $f(1)$

In exercises 26 - 29, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

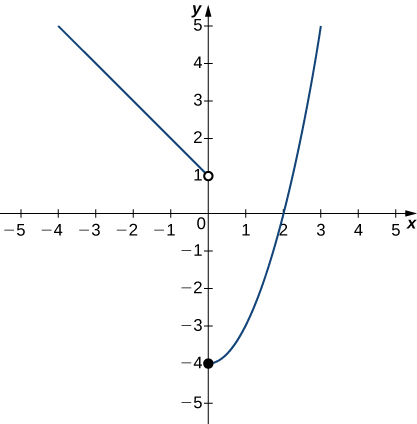
$A graph of a piecewise function with two segments. The first is a linear function for x < 0. There is an open circle at (0,1), and its slope is -1. The second segment is the right half of a parabola opening upward. Its vertex is a closed circle at (0, -4), and it goes through the point (2,0).$

26) $\displaystyle \lim_{x→0^−}f(x)$

Answer: $1$

27) $\displaystyle \lim_{x→0^+}f(x)$

28) $\displaystyle \lim_{x→0}f(x)$

Answer: DNE

29) $\displaystyle \lim_{x→2}f(x)$

In exercises 30 - 35, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

$A graph of a piecewise function with three segments, all linear. The first exists for x < -2, has a slope of 1, and ends at the open circle at (-2, 0). The second exists over the interval [-2, 2], has a slope of -1, goes through the origin, and has closed circles at its endpoints (-2, 2) and (2,-2). The third exists for x>2, has a slope of 1, and begins at the open circle (2,2).$

30) $\displaystyle \lim_{x→−2^−}f(x)$

Answer: $0$

31) $\displaystyle \lim_{x→−2^+}f(x)$

32) $\displaystyle \lim_{x→−2}f(x)$

Answer: DNE

33) $\displaystyle \lim_{x→2^−}f(x)$

34) $\displaystyle \lim_{x→2^+}f(x)$

Answer: $2$

35) $\displaystyle \lim_{x→2}f(x)$

In exercises 36 - 38, use the graph of the function $y=g(x)$ shown here to find the values, if possible. Estimate when necessary.

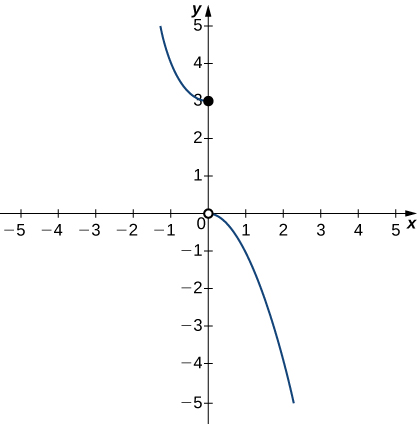
$A graph of a piecewise function with two segments. The first exists for x>=0 and is the left half of an upward opening parabola with vertex at the closed circle (0,3). The second exists for x>0 and is the right half of a downward opening parabola with vertex at the open circle (0,0).$

36) $\displaystyle \lim_{x→0^−}g(x)$

Answer: $3$

37) $\displaystyle \lim_{x→0^+}g(x)$

38) $\displaystyle \lim_{x→0}g(x)$

Answer: DNE

In exercises 39 - 41, use the graph of the function $y=h(x)$ shown here to find the values, if possible. Estimate when necessary.

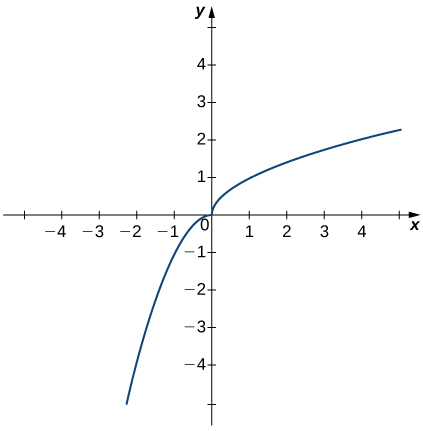
$A graph of a function with two curves approaching 0 from quadrant 1 and quadrant 3. The curve in quadrant one appears to be the top half of a parabola opening to the right of the y axis along the x axis with vertex at the origin. The curve in quadrant three appears to be the left half of a parabola opening downward with vertex at the origin.$

39) $\displaystyle \lim_{x→0^−}h(x)$

40) $\displaystyle \lim_{x→0^+}h(x)$

Answer: $0$

41) $\displaystyle \lim_{x→0}h(x)$

In exercises 42 - 46, use the graph of the function $y=f(x)$ shown here to find the values, if possible. Estimate when necessary.

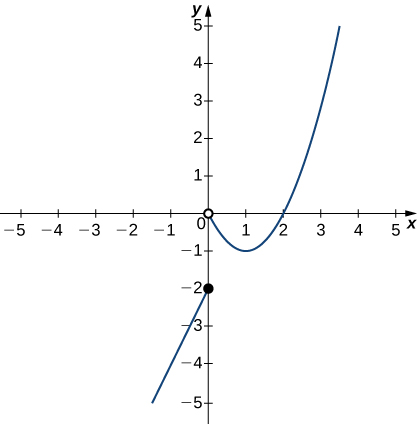
$A graph with a curve and a point. The point is a closed circle at (0,-2). The curve is part of an upward opening parabola with vertex at (1,-1). It exists for x > 0, and there is a closed circle at the origin.$

42) $\displaystyle \lim_{x→0^−}f(x)$

Answer: $-2$

43) $\displaystyle \lim_{x→0^+}f(x)$

44) $\displaystyle \lim_{x→0}f(x)$

Answer: DNE

45) $\displaystyle \lim_{x→1}f(x)$

46) $\displaystyle \lim_{x→2}f(x)$

Answer: $0$

Infinite Limits

In exercises 47 - 51, sketch the graph of a function with the given properties.

47) $\displaystyle \lim_{x→2}f(x)=1, \quad \lim_{x→4^−}f(x)=3, \quad \lim_{x→4^+}f(x)=6, \quad x=4$ is not defined.

48) $\displaystyle \lim_{x→−∞}f(x)=0, \quad \lim_{x→−1^−}f(x)=−∞, \quad \lim_{x→−1^+}f(x)=∞,\quad \lim_{x→0}f(x)=f(0), \quad f(0)=1, \quad \lim_{x→∞}f(x)=−∞$

Answer

Answers may vary

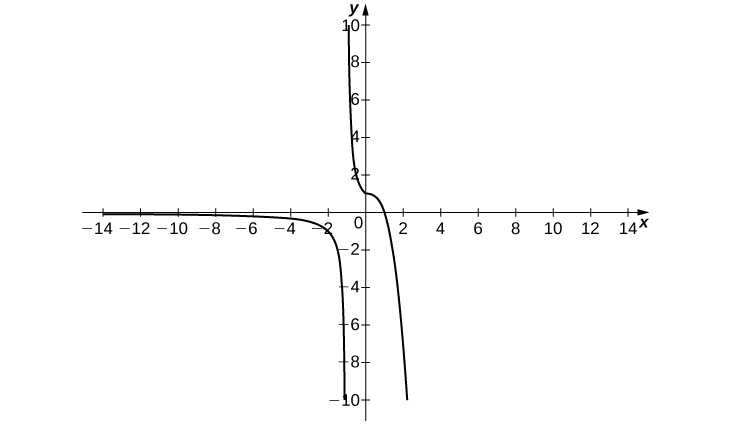
$A graph of a piecewise function with two segments. The first segment is in quadrant three and asymptotically goes to negative infinity along the y axis and 0 along the x axis. The second segment consists of two curves. The first appears to be the left half of an upward opening parabola with vertex at (0,1). The second appears to be the right half of a downward opening parabola with vertex at (0,1) as well.$

49) $\displaystyle \lim_{x→−∞}f(x)=2, \quad \lim_{x→3^−}f(x)=−∞, \quad \lim_{x→3^+}f(x)=∞, \quad \lim_{x→∞}f(x)=2, \quad f(0)=-\frac{1}{3}$

50) $\displaystyle \lim_{x→−∞}f(x)=2,\quad \lim_{x→−2}f(x)=−∞,\quad \lim_{x→∞}f(x)=2,\quad f(0)=0$

Answer

Answer may vary

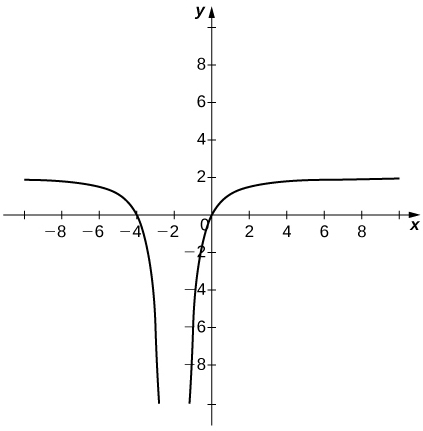
$A graph containing two curves. The first goes to 2 asymptotically along y=2 and to negative infinity along x = -2. The second goes to negative infinity along x=-2 and to 2 along y=2.$

51) $\displaystyle \lim_{x→−∞}f(x)=0,\quad \lim_{x→−1^−}f(x)=∞,\quad \lim_{x→−1^+}f(x)=−∞, \quad f(0)=−1, \quad \lim_{x→1^−}f(x)=−∞, \quad \lim_{x→1^+}f(x)=∞, \quad \lim_{x→∞}f(x)=0$

52) Shock waves arise in many physical applications, ranging from supernovas to detonation waves. A graph of the density of a shock wave with respect to distance, $x$, is shown here. We are mainly interested in the location of the front of the shock, labeled $X_{SF}$ in the diagram.

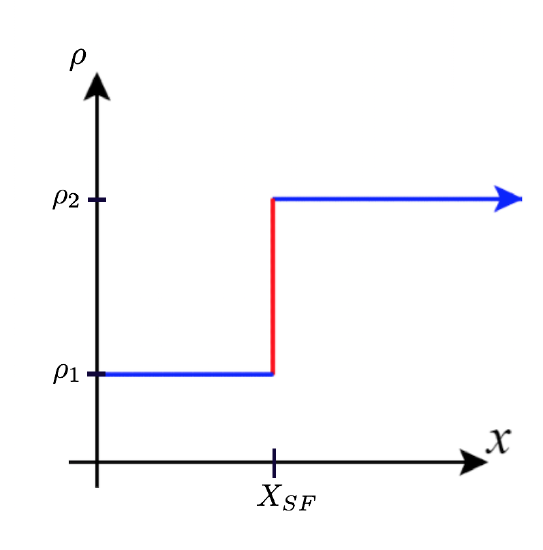
$A graph in quadrant one of the density of a shockwave with three labeled points: p1 and p2 on the y axis, with p1 > p2, and xsf on the x axis. It consists of y= p1 from 0 to xsf, x = xsf from y= p1 to y=p2, and y=p2 for values greater than or equal to xsf.$

a. Evaluate $\displaystyle \lim_{x→X_{SF}^+}ρ(x)$.

b. Evaluate $\displaystyle \lim_{x→X_{SF}^−}ρ(x)$.

c. Evaluate $\displaystyle \lim_{x→X_{SF}}ρ(x)$. Explain the physical meanings behind your answers.

Answer: a. $ρ_2$ b. $ρ_1$ c. DNE unless $ρ_1=ρ_2$. As you approach $X_{SF}$ from the right, you are in the high-density area of the shock. When you approach from the left, you have not experienced the “shock” yet and are at a lower density.

53) A track coach uses a camera with a fast shutter to estimate the position of a runner with respect to time. A table of the values of position of the athlete versus time is given here, where $x$ is the position in meters of the runner and $t$ is time in seconds. What is $\displaystyle \lim_{t→2}x(t)$? What does it mean physically?

$t(sec)$	$x(m)$
1.75	4.5
1.95	6.1
1.99	6.42
2.01	6.58
2.05	6.9
2.25	8.5

Search

Text Color

Text Size

Margin Size

Font Type

Intuitive Definition of Limits

Infinite Limits