4.6E: Exercises for Section 4.6
( \newcommand{\kernel}{\mathrm{null}\,}\)
selected template will load here
This action is not available.

( \newcommand{\kernel}{\mathrm{null}\,}\)
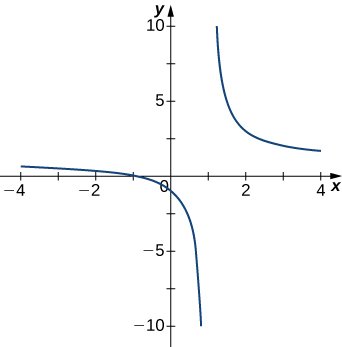
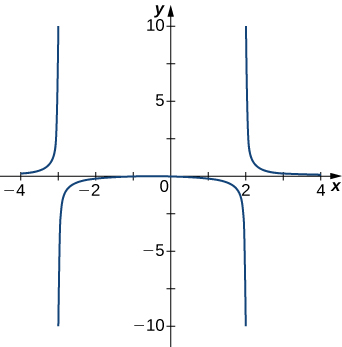
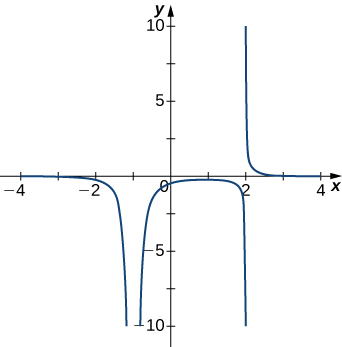
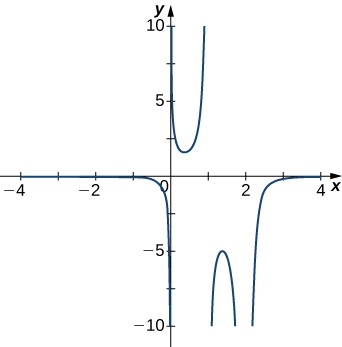
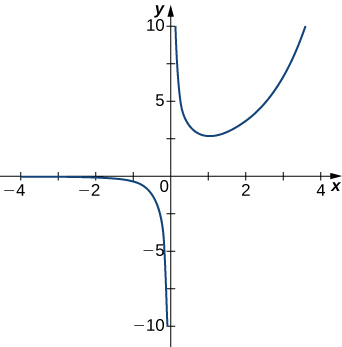
For exercises 1 - 5, examine the graphs. Identify where the vertical asymptotes are located.
1)
2)
3)
4)
5)
For the functions
6)
7)
8)
9)
10)
In exercises 11 - 20, evaluate the limit.
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
For exercises 21 - 25, find the horizontal and vertical asymptotes.
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
31)
32)
33)
34)
For exercises 35 - 38, construct a function
35)
36)
37)
38)
In exercises 39 - 43, graph the function on a graphing calculator on the window
39) [T]
40) [T]
41) [T]
42) [T]
43) [T]
In exercises 44 - 55, draw a graph of the functions without using a calculator. Be sure to notice all important features of the graph: local maxima and minima, inflection points, and asymptotic behavior.
44)
45)
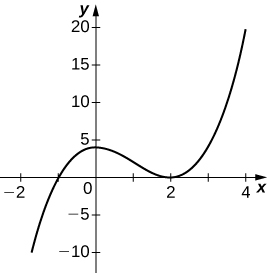
46)
47)
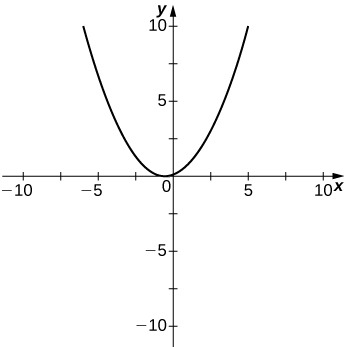
48)
49)
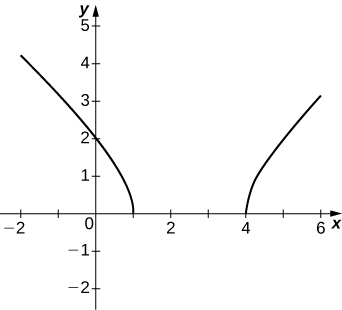
50)
51)
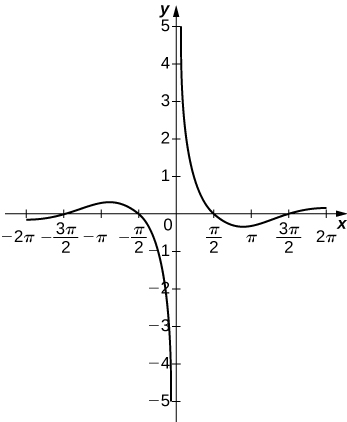
52)
53)
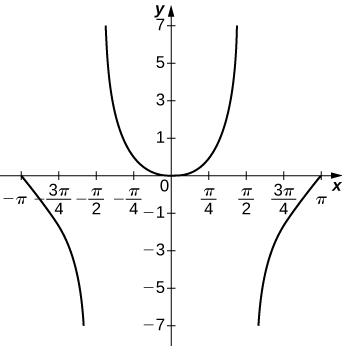
54)
55)
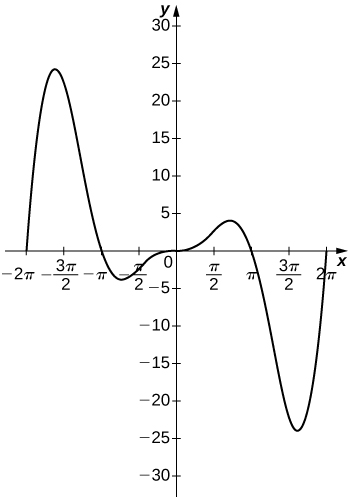
56) For
57) For
58) If
59) Both
60) True or false: Every ratio of polynomials has vertical asymptotes.

