5.7E: Exercises for Section 5.7

Last updated
Save as PDF

Page ID: 120774

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 6, evaluate each integral in terms of an inverse trigonometric function.

1) $\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}$

Answer: $\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \sin^{−1}x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}$

2) $\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}$

3) $\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{1+x^2}$

Answer: $\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{1+x^2} \quad = \quad \tan^{−1}x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}$

4) $\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}$

5) $\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Answer: $\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \sec^{−1}x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}$

6) $\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

In exercises 7 - 12, find each indefinite integral, using appropriate substitutions.

7) $\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}$

Answer: $\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \sin^{−1}\left(\frac{x}{3}\right)+C$

8) $\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}$

9) $\displaystyle ∫\frac{dx}{9+x^2}$

Answer: $\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\tan^{−1}\left(\frac{x}{3}\right)+C$

10) $\displaystyle ∫\frac{dx}{25+16x^2}$

11) $\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}$

Answer: $\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\sec^{−1}\left(\frac{|x|}{3}\right)+C$

12) $\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}$

13) Explain the relationship $\displaystyle −\cos^{−1}t+C=∫\frac{dt}{\sqrt{1−t^2}}=\sin^{−1}t+C.$ Is it true, in general, that $\cos^{−1}t=−\sin^{−1}t$?

Answer: $\cos(\frac{π}{2}−θ)=\sin θ.$ So, $\sin^{−1}t=\dfrac{π}{2}−\cos^{−1}t.$ They differ by a constant.

14) Explain the relationship $\displaystyle \sec^{−1}t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\csc^{−1}t+C.$ Is it true, in general, that $\sec^{−1}t=−\csc^{−1}t$?

15) Explain what is wrong with the following integral: $\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}$.

Answer: $\sqrt{1−t^2}$ is not defined as a real number when $t>1$.

16) Explain what is wrong with the following integral: $\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}$.

Answer: $\sqrt{t^2−1}$ is not defined as a real number when $-1 \lt t \lt 1$, and the integrand is undefined when $t = -1$ or $t = 1$.

In exercises 17 - 20, solve for the antiderivative of $f$ with $C=0$, then use a calculator to graph $f$ and the antiderivative over the given interval $[a,b]$. Identify a value of $C$ such that adding $C$ to the antiderivative recovers the definite integral $\displaystyle F(x)=∫^x_af(t)\,dt$.

17) [T] $\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx$ over $[−3,3]$

Answer

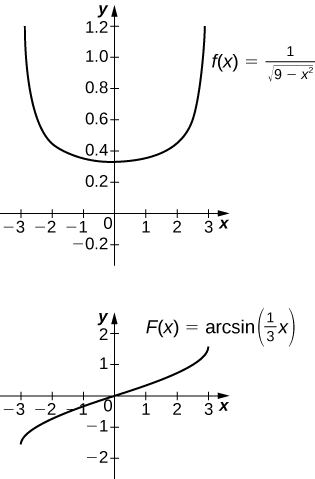
$Two graphs. The first shows the function f(x) = 1 / sqrt(9 – x^2). It is an upward opening curve symmetric about the y axis, crossing at (0, 1/3). The second shows the function F(x) = arcsin(1/3 x). It is an increasing curve going through the origin.$

The antiderivative is $ \sin^{−1}(\frac{x}{3})+C$. Taking $C=\frac{π}{2}$ recovers the definite integral.

18) [T] $\displaystyle ∫\frac{9}{9+x^2}\,dx$ over $[−6,6]$

19) [T] $\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx$ over $[−6,6]$

Answer

$Two graphs. The first shows the function f(x) = cos(x) / (4 + sin(x)^2). It is an oscillating function over [-6, 6] with turning points at roughly (-3, -2.5), (0, .25), and (3, -2.5), where (0,.25) is a local max and the others are local mins. The second shows the function F(x) = .5 * arctan(.5*sin(x)), which also oscillates over [-6,6]. It has turning points at roughly (-4.5, .25), (-1.5, -.25), (1.5, .25), and (4.5, -.25).$

The antiderivative is $\frac{1}{2}\tan^{−1}(\frac{\sin x}{2})+C$. Taking $C=\frac{1}{2}\tan^{−1}(\frac{\sin(6)}{2})$ recovers the definite integral.

20) [T] $\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx$ over $[−6,6]$

In exercises 21 - 26, compute the antiderivative using appropriate substitutions.

21) $\displaystyle ∫\frac{\sin^{−1}t}{\sqrt{1−t^2}}\,dt$

Answer: $\displaystyle ∫\frac{\sin^{−1}t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\sin^{−1}t)^2+C$

22) $\displaystyle ∫\frac{dt}{\sin^{−1} t\sqrt{1−t^2}}$

23) $\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt$

Answer: $\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\tan^{−1}(2t))^2+C$

24) $\displaystyle ∫\frac{t\tan^{−1}(t^2)}{1+t^4}\,dt$

25) $\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt$

Answer: $\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\sec^{−1}\left(\tfrac{t}{2}\right))^2+C$

26) $\displaystyle ∫\frac{t\sec^{−1}(t^2)}{t^2\sqrt{t^4−1}}\,dt$

In exercises 27 - 32, use a calculator to graph the antiderivative of $f$ with $C=0$ over the given interval $[a,b].$ Approximate a value of $C$, if possible, such that adding $C$ to the antiderivative gives the same value as the definite integral $\displaystyle F(x)=∫^x_af(t)\,dt.$

27) [T] $\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx$ over $[2,6]$

Answer

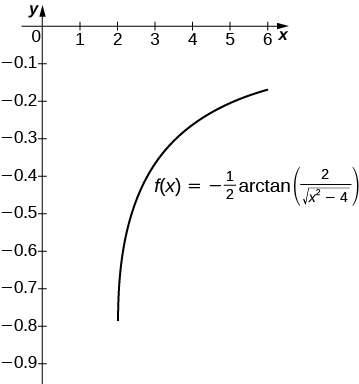
$A graph of the function f(x) = -.5 * arctan(2 / ( sqrt(x^2 – 4) ) ) in quadrant four. It is an increasing concave down curve with a vertical asymptote at x=2.$

The antiderivative is $\frac{1}{2}\sec^{−1}(\frac{x}{2})+C$. Taking $C=0$ recovers the definite integral over $ [2,6]$.

28) [T] $\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx$ over $[0,6]$

29) [T] $\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}$ over $ [−6,6]$

Answer

$The graph of f(x) = arctan(x sin(x)) over [-6,6]. It has five turning points at roughly (-5, -1.5), (-2,1), (0,0), (2,1), and (5,-1.5).$

The general antiderivative is $\tan^{−1}(x\sin x)+C$. Taking $C=−\tan^{−1}(6\sin(6))$ recovers the definite integral.

30) [T] $\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx$ over $[0,2]$

31) [T] $\displaystyle ∫\frac{1}{x+x\ln 2x}$ over $[0,2]$

Answer

$A graph of the function f(x) = arctan(ln(x)) over (0, 2]. It is an increasing curve with x-intercept at (1,0).$

The general antiderivative is $\tan^{−1}(\ln x)+C$. Taking $\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\tan^{−1} t$ recovers the definite integral.

32) [T] $\displaystyle ∫\frac{\sin^{−1}x}{\sqrt{1−x^2}}$ over $[−1,1]$

In exercises 33 - 38, compute each integral using appropriate substitutions.

33) $\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt$

Answer: $\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \sin^{−1}(e^t)+C$

34) $\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt$

35) $\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}$

Answer: $\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \sin^{−1}(\ln t)+C$

36) $\displaystyle ∫\frac{dt}{t(1+\ln^2t)}$

37) $\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt$

Answer: $\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\cos^{−1}(2t))^2+C$

38) $\displaystyle ∫\frac{e^t\cos^{−1}(e^t)}{\sqrt{1−e^{2t}}}\,dt$

In exercises 39 - 42, compute each definite integral.

39) $\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt$

Answer: $\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)$

40) $\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\cos^{−1}t)}{\sqrt{1−t^2}}\,dt$

41) $\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt$

Answer: $\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}$

42) $\displaystyle ∫^{1/2}_0\frac{\cos(\tan^{−1}t)}{1+t^2}\,dt$

43) For $A>0$, compute $\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}$ and evaluate $\displaystyle \lim_{a→∞}I(A)$, the area under the graph of $\dfrac{1}{1+t^2}$ on $[−∞,∞]$.

Answer: $2\tan^{−1}(A)→π$ as $A→∞$

44) For $1<B<∞$, compute $\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}$ and evaluate $\displaystyle \lim_{B→∞}I(B)$, the area under the graph of $\frac{1}{t\sqrt{t^2−1}}$ over $[1,∞)$.

45) Use the substitution $u=\sqrt{2}\cot x$ and the identity $1+\cot^2x=\csc^2x$ to evaluate $\displaystyle ∫\frac{dx}{1+\cos^2x}$. (Hint: Multiply the top and bottom of the integrand by $\csc^2x$.)

Answer: Using the hint, one has $\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.$ Set $u=\sqrt{2}\cot x.$ Then, $du=−\sqrt{2}\csc^2x$ and the integral is $\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\tan^{−1}u+C=\tfrac{\sqrt{2}}{2}\tan^{−1}(\sqrt{2}\cot x)+C$. If one uses the identity $\tan^{−1}s+\tan^{−1}(\frac{1}{s})=\frac{π}{2}$, then this can also be written $\tfrac{\sqrt{2}}{2}\tan^{−1}(\frac{\tan x}{\sqrt{2}})+C.$

46) [T] Approximate the points at which the graphs of $f(x)=2x^2−1$ and $g(x)=(1+4x^2)^{−3/2}$ intersect, and approximate the area between their graphs accurate to three decimal places.

47) [T] Approximate the points at which the graphs of $f(x)=x^2−1$ and $f(x)=x^2−1$ intersect, and approximate the area between their graphs accurate to three decimal places.

Answer: $x≈±1.13525.$ The left endpoint estimate with $N=100$ is 2.796 and these decimals persist for $N=500$.

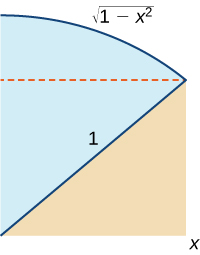
48) Use the following graph to prove that $\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\sin^{−1}x.$

$A diagram containing two shapes, a wedge from a circle shaded in blue on top of a triangle shaded in brown. The triangle’s hypotenuse is one of the radii edges of the wedge of the circle and is 1 unit long. There is a dotted red line forming a rectangle out of part of the wedge and the triangle, with the hypotenuse of the triangle as the diagonal of the rectangle. The curve of the circle is described by the equation sqrt(1-x^2).$

Search

Text Color

Text Size

Margin Size

Font Type