5.6E: Exercises for Section 5.6

For exercises 1 - 8, compute each indefinite integral.

1) $\displaystyle ∫e^{2x}\,dx$

2) $\displaystyle ∫e^{−3x}\,dx$

Answer

$\displaystyle ∫e^{−3x}\,dx \quad = \quad \frac{−1}{3}e^{−3x}+C$

3) $\displaystyle ∫2^x\,dx$

4) $\displaystyle ∫3^{−x}\,dx$

Answer

$\displaystyle ∫3^{−x}\,dx \quad = \quad −\frac{3^{−x}}{\ln 3}+C$

5) $\displaystyle ∫\frac{1}{2x}\,dx$

6) $\displaystyle ∫\frac{2}{x}\,dx$

Answer

$\displaystyle ∫\frac{2}{x}\,dx \quad = \quad 2\ln x+C \quad = \quad \ln(x^2)+C$

7) $\displaystyle ∫\frac{1}{x^2}\,dx$

8) $\displaystyle ∫\frac{1}{\sqrt{x}}\,dx$

Answer

$\displaystyle ∫\frac{1}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}+C$

In exercises 9 - 16, find each indefinite integral by using appropriate substitutions.

9) $\displaystyle ∫\frac{\ln x}{x}\,dx$

10) $\displaystyle ∫\frac{dx}{x(\ln x)^2}$

Answer

$\displaystyle ∫\frac{dx}{x(\ln x)^2} \quad = \quad −\frac{1}{\ln x}+C$

11) $\displaystyle ∫\frac{dx}{x\ln x}\quad (x>1)$

12) $\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)}$

Answer

$\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)} \quad = \quad \ln(\ln(\ln x))+C$

13) $\displaystyle ∫\tan θ\,dθ$

14) $\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx$

Answer

$\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx \quad = \quad \ln(x\cos x)+C$

15) $\displaystyle ∫\frac{\ln(\sin x)}{\tan x}\,dx$

16) $\displaystyle ∫\ln(\cos x)\tan x\,dx$

Answer

$\displaystyle ∫\ln(\cos x)\tan x\,dx \quad = \quad −\dfrac{1}{2}(\ln(\cos(x)))^2+C$

17) $\displaystyle ∫xe^{−x^2}\,dx$

18) $\displaystyle ∫x^2e^{−x^3}\,dx$

Answer

$\displaystyle ∫x^2e^{−x^3}\,dx \quad = \quad \dfrac{−e^{−x^3}}{3}+C$

19) $\displaystyle ∫e^{\sin x}\cos x\,dx$

20) $\displaystyle ∫e^{\tan x}\sec^2 x\,dx$

Answer

$\displaystyle ∫e^{\tan x}\sec^2 x\,dx\quad = \quad e^{\tan x}+C$

21) $\displaystyle ∫\frac{e^{\ln x}}{x}\,dx$

22) $\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt$

Answer

$\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt = \int \frac{1-t}{1-t}\,dt = \int 1\, dt \quad = \quad t+C$

In exercises 23 - 28, verify by differentiation that $\displaystyle ∫\ln x\,dx=x(\ln x−1)+C$, then use appropriate changes of variables to compute the integral.

23) $\displaystyle ∫\ln x\,dx$ (Hint: $\displaystyle ∫\ln x\,dx=\frac{1}{2}∫x\ln(x^2)\,dx$)

24) $\displaystyle ∫x^2\ln^2 x\,dx$

Answer

$\displaystyle ∫x^2\ln^2 x\,dx \quad = \quad \dfrac{1}{9}x^3(\ln(x^3)−1)+C$

25) $\displaystyle ∫\frac{\ln x}{x^2}\,dx$ (Hint: Set $u=\dfrac{1}{x}.)$

26) $\displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx$ (Hint: Set $u=\sqrt{x}.)$

Answer

$\displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}(\ln x−2)+C$

27) Write an integral to express the area under the graph of $y=\dfrac{1}{t}$ from $t=1$ to $e^x$ and evaluate the integral.

28) Write an integral to express the area under the graph of $y=e^t$ between $t=0$ and $t=\ln x$, and evaluate the integral.

Answer

$\displaystyle ∫^{\ln x}_0e^t\,dt=e^t\bigg|^{\ln x}_0=e^{\ln x}−e^0=x−1$

In exercises 29 - 35, use appropriate substitutions to express the trigonometric integrals in terms of compositions with logarithms.

29) $\displaystyle ∫\tan(2x)\,dx$

30) $\displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx$

Answer

$\displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx \quad = \quad −\frac{1}{3}\ln|\sin(3x)+\cos(3x)| + C$

31) $\displaystyle ∫\frac{x\sin(x^2)}{\cos(x^2)}\,dx$

32) $\displaystyle ∫x\csc(x^2)\,dx$

Answer

$\displaystyle ∫x\csc(x^2)\,dx \quad = \quad −\frac{1}{2}\ln∣\csc(x^2)+\cot(x^2)∣+C$

33) $\displaystyle ∫\ln(\cos x)\tan x\,dx$

34) $\displaystyle ∫\ln(\csc x)\cot x\,dx$

Answer

$\displaystyle ∫\ln(\csc x)\cot x\,dx \quad = \quad −\frac{1}{2}(\ln(\csc x))^2+C$

35) $\displaystyle ∫\frac{e^x−e^{−x}}{e^x+e^{−x}}\,dx$

In exercises 36 - 40, evaluate the definite integral.

36) $\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx$

Answer

$\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx \quad = \quad \frac{1}{3}\ln\left(\tfrac{26}{7}\right)$

37) $\displaystyle ∫^{π/4}_0\tan x\,dx$

Answer

$\displaystyle ∫^{π/4}_0\tan x\,dx= \ln\sqrt{2}$

38) $\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx$

Answer

$\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx \quad = \quad \ln(\sqrt{3}−1)$

39) $\displaystyle ∫^{π/3}_{π/4}\sec x\,dx$

Answer

$\displaystyle ∫^{π/3}_{π/4}\sec x\,dx \quad = \quad \ln\left(\frac{3}{\sqrt{6}+\sqrt{3}}\right)$

40) $\displaystyle ∫^{π/3}_{π/4}\cot x\,dx$

Answer

$\displaystyle ∫^{π/3}_{π/4}\cot x\,dx \quad = \quad \frac{1}{2}\ln\frac{3}{2}$

In exercises 41 - 46, integrate using the indicated substitution.

41) $\displaystyle ∫\frac{x}{x−100}\,dx;\quad u=x−100$

42) $\displaystyle ∫\frac{y−1}{y+1}\,dy;\quad u=y+1$

Answer

$\displaystyle ∫\frac{y−1}{y+1}\,dy \quad = \quad y−2\ln|y+1|+C$

43) $\displaystyle ∫\frac{1−x^2}{3x−x^3}\,dx;\quad u=3x−x^3$

44) $\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx;\quad u=\sin x−\cos x$

Answer

$\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx \quad=\quad \ln|\sin x−\cos x|+C$

45) $\displaystyle ∫e^{2x}\sqrt{1−e^{2x}}\,dx;\quad u=1−e^{2x}$

46) $\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx;\quad u=1−(\ln x)^2$

Answer

$\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx \quad = \quad −\frac{1}{3}(1−(\ln x^2))^{3/2}+C$

47) $\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx; \quad u = \sqrt{x} + 2$

Answer

$\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx \quad = \quad \left( \sqrt{x} + 2 \right)^2 - 8\left( \sqrt{x} + 2 \right) + 8\ln\left( \sqrt{x} + 2 \right) + C$

48) $\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx; \quad u = e^{x} + 1$

Answer

$\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx \quad = \quad \sec(e^x+1) + C$

In exercises 49 - 54, state whether the right-endpoint approximation overestimates or underestimates the exact area. Then calculate the right endpoint estimate $R_{50}$ and solve for the exact area.

49) [T] $y=e^x$ over $[0,1]$

50) [T] $y=e^{−x}$ over $[0,1]$

Answer

Since $f$ is decreasing, the right endpoint estimate underestimates the area.
Exact solution: $\dfrac{e−1}{e},\quad R_{50}=0.6258$.

51) [T] $y=\ln(x)$ over $[1,2]$

52) [T] $y=\dfrac{x+1}{x^2+2x+6}$ over $[0,1]$

Answer

Since $f$ is increasing, the right endpoint estimate overestimates the area.
Exact solution: $\dfrac{2\ln(3)−\ln(6)}{2},\quad R_{50}=0.2033.$

53) [T] $y=2^x$ over $[−1,0]$

54) [T] $y=−2^{−x}$ over $[0,1]$

Answer

Since $f$ is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).
Exact solution: $−\dfrac{1}{\ln(4)},\quad R_{50}=−0.7164.$

In exercises 55 - 58, $f(x)≥0$ for $a≤x≤b$. Find the area under the graph of $f(x)$ between the given values $a$ and $b$ by integrating.

55) $f(x)=\dfrac{\log_{10}(x)}{x};\quad a=10,b=100$

56) $f(x)=\dfrac{\log_2(x)}{x};\quad a=32,b=64$

Answer

$\dfrac{11}{2}\ln 2$

57) $f(x)=2^{−x};\quad a=1,b=2$

58) $f(x)=2^{−x};\quad a=3,b=4$

Answer

$\dfrac{1}{\ln(65,536)}$

59) Find the area under the graph of the function $f(x)=xe^{−x^2}$ between $x=0$ and $x=5$.

60) Compute the integral of $f(x)=xe^{−x^2}$ and find the smallest value of $N$ such that the area under the graph $f(x)=xe^{−x^2}$ between $x=N$ and $x=N+10$ is, at most, $0.01$.

Answer

$\displaystyle ∫^{N+1}_Nxe^{−x^2}\,dx=\frac{1}{2}(e^{−N^2}−e^{−(N+1)^2}).$ The quantity is less than $0.01$ when $N=2$.

61) Find the limit, as $N$ tends to infinity, of the area under the graph of $f(x)=xe^{−x^2}$ between $x=0$ and $x=5$.

62) Show that $\displaystyle ∫^b_a\frac{dt}{t}=∫^{1/a}_{1/b}\frac{dt}{t}$ when $0<a≤b$.

Answer

$\displaystyle ∫^b_a\frac{dx}{x}=\ln(b)−\ln(a)=\ln(\frac{1}{a})−\ln(\frac{1}{b})=∫^{1/a}_{1/b}\frac{dx}{x}$

63) Suppose that $f(x)>0$ for all $x$ and that $f$ and $g$ are differentiable. Use the identity $f^g=e^{g\ln f}$ and the chain rule to find the derivative of $f^g$.

64) Use the previous exercise to find the antiderivative of $h(x)=x^x(1+\ln x)$ and evaluate $\displaystyle ∫^3_2x^x(1+\ln x)\,dx$.

Answer

23

65) Show that if $c>0$, then the integral of $\frac{1}{x}$ from $ac$ to $bc$ $(\text{for}\,0<a<b)$ is the same as the integral of $\frac{1}{x}$ from $a$ to $b$.

The following exercises are intended to derive the fundamental properties of the natural log starting from the definition $\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$, using properties of the definite integral and making no further assumptions.

66) Use the identity $\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$ to derive the identity $\ln\left(\dfrac{1}{x}\right)=−\ln x$.

Answer

We may assume that $x>1$,so $\dfrac{1}{x}<1.$ Then, $\displaystyle ∫^{1/x}_{1}\frac{dt}{t}$. Now make the substitution $u=\dfrac{1}{t}$, so $du=−\dfrac{dt}{t^2}$ and $\dfrac{du}{u}=−\dfrac{dt}{t}$, and change endpoints: $\displaystyle ∫^{1/x}_1\frac{dt}{t}=−∫^x_1\frac{du}{u}=−\ln x.$

67) Use a change of variable in the integral $\displaystyle ∫^{xy}_1\frac{1}{t}\,dt$ to show that $\ln xy=\ln x+\ln y$ for $x,y>0$.

68) Use the identity $\displaystyle \ln x=∫^x_1\frac{dt}{x}$ to show that $\ln(x)$ is an increasing function of $x$ on $[0,∞)$, and use the previous exercises to show that the range of $\ln(x)$ is $(−∞,∞)$. Without any further assumptions, conclude that $\ln(x)$ has an inverse function defined on $(−∞,∞).$

69) Pretend, for the moment, that we do not know that $e^x$ is the inverse function of $\ln(x)$, but keep in mind that $\ln(x)$ has an inverse function defined on $(−∞,∞)$. Call it $E$. Use the identity $\ln xy=\ln x+\ln y$ to deduce that $E(a+b)=E(a)E(b)$ for any real numbers $a$, $b$.

70) Pretend, for the moment, that we do not know that $e^x$ is the inverse function of $\ln x$, but keep in mind that $\ln x$ has an inverse function defined on $(−∞,∞)$. Call it $E$. Show that $E'(t)=E(t).$

Answer

$x=E(\ln(x)).$ Then, $1=\dfrac{E'(\ln x)}{x}$ or $x=E'(\ln x)$. Since any number $t$ can be written $t=\ln x$ for some $x$, and for such $t$ we have $x=E(t)$, it follows that for any $t,\,E'(t)=E(t).$

71) The sine integral, defined as $\displaystyle S(x)=∫^x_0\frac{\sin t}{t}\,dt$ is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large $x$. Show that for $k≥1,\quad |S(2πk)−S(2π(k+1))|≤\dfrac{1}{k(2k+1)π}.$ (Hint: $\sin(t+π)=−\sin t$)

72) [T] The normal distribution in probability is given by $p(x)=\dfrac{1}{σ\sqrt{2π}}e^{−(x−μ)^2/2σ^2}$, where $σ$ is the standard deviation and $μ$ is the average. The standard normal distribution in probability, $p_s$, corresponds to $μ=0$ and $σ=1$. Compute the left endpoint estimates $R_{10}$ and $R_{100}$ of $\displaystyle ∫^1_{−1}\frac{1}{\sqrt{2π}}e^{−x^{2/2}}\,dx.$

Answer

$R_{10}=0.6811,\quad R_{100}=0.6827$

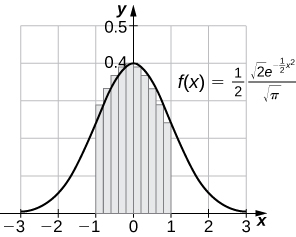
73) [T] Compute the right endpoint estimates $R_{50}$ and $R_{100}$ of $\displaystyle ∫^5_{−3}\frac{1}{2\sqrt{2π}}e^{−(x−1)^2/8}$.

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

• Paul Seeburger (Monroe Community College) added problems 47-48 to Section 5.6 exercises.